VNA GUI Reference
R&S
®
ZNL/ZNLE
388
User Manual 1178.5966.02 ─ 07
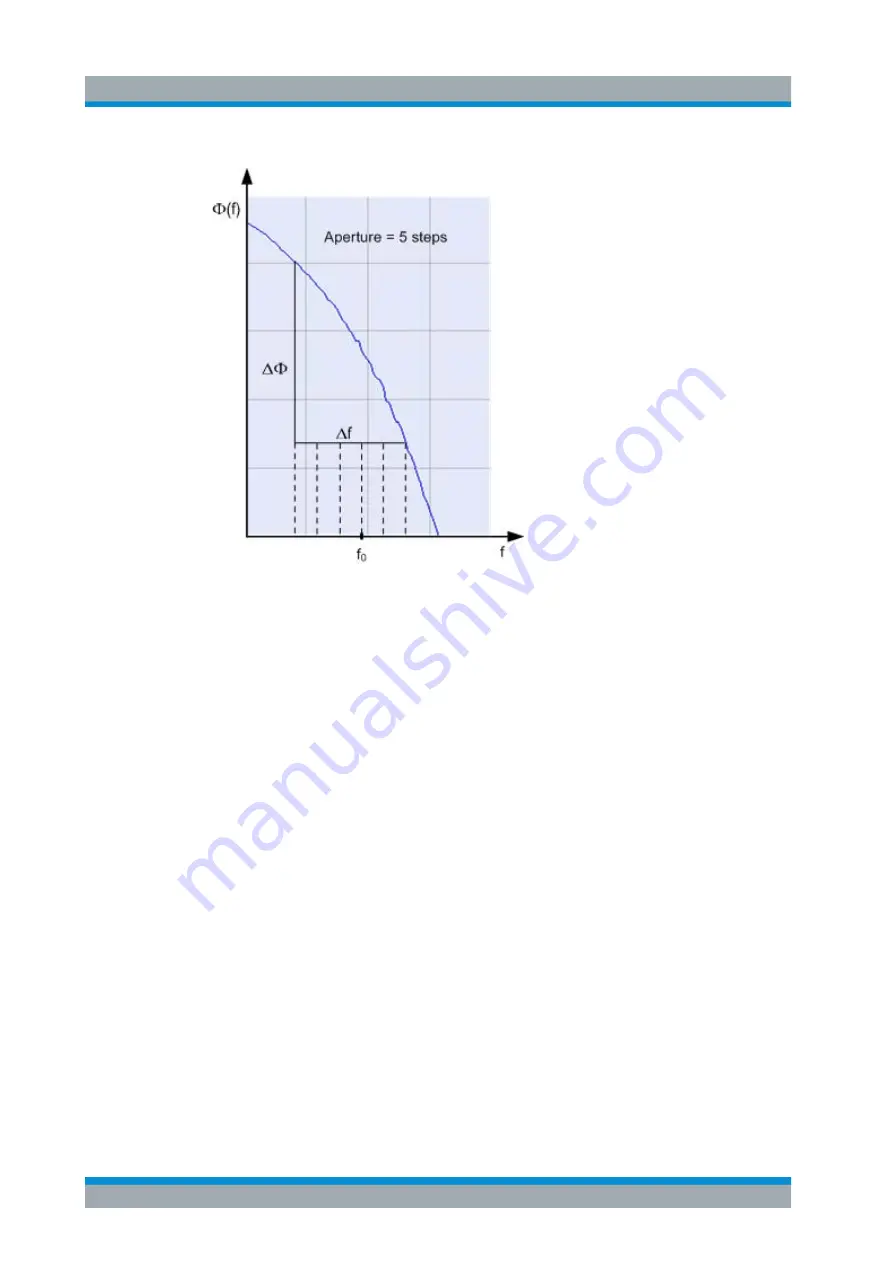
Calculation of Δf and ΔΦ
With n sweep steps the delay at sweep point no. m is calculated as follows:
●
If n is even (n = 2k), then Δf (m) = f (m+k) – f (m–k) and ΔΦ(m) = ΔΦ (m+k) – ΔΦ
(m–k).
●
If n is odd (n = 2k+1), then Δf (m) = f (m+k) – f (m–k–1) and ΔΦ (m) = ΔΦ (m+k) –
ΔΦ (m–k–1).
The calculated phase difference (and thus the group delay) is always assigned to the
frequency point no. m.
For linear sweeps, if the number of aperture steps is odd, then the center of the aper-
ture range is [f (m+k) + f (m–k–1)] / 2 = f (m–1/2). I.e. the center is half a frequency
step below the sweep point f (m). Hence, toggling from even to odd numbers of aper-
ture steps and back can virtually shift the group delay curve towards higher/lower fre-
quencies. It is recommended, to use even numbers of aperture steps, especially for
large frequency step sizes.
The delay calculation is based on the already measured sweep points and does not
slow down the measurement.
Δf is constant over the entire sweep range, if the sweep type is a Lin. Frequency
sweep. For Log. Frequency and Segmented Frequency sweeps, it varies with the
sweep point number m.
Application:
The aperture must be adjusted to the conditions of the measurement. A
small aperture increases the noise in the group delay; a large aperture tends to mini-
mize the effects of noise and phase uncertainty, but at the expense of frequency reso-
lution. Phase distortions (i.e. deviations from linear phase) which are narrower in fre-
quency than the aperture tend to be smeared over and cannot be measured.
Remote command:
CALCulate<Chn>:GDAPerture:SCOunt
Format Softtool
www.allice.de
Allice Messtechnik GmbH






























