Functions
138
7UM62 Manual
C53000-G1176-C149-3
The current
I
is independent of the location of the measurement:
The voltage U at the location of measurement m is:
Thus results with:
where
δ
is the displacement angle between the generator voltage and the network
equivalent voltage. Under normal conditions, this angle depends on the load situation
and is nearly constant. It fluctuates during power swings and can vary, in case of an
out-of-step condition, between 0°
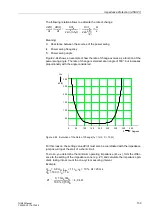
and 360°. Figure 2-66 shows the trajectory of the
impedance vector at the measurement location m according to the above formula. The
origin of the coordinate system corresponds to the measurement location (voltage
transformer set). When the ratio of the voltage magnitudes U
N
/U
G
is kept constant and
the load angle
δ
varies, then circles result as a locus diagram. The centre and the
radius of the circle are determined by the ratio U
N
/U
G
. The centre points are situated
on a line which is determined by Z
tot
. Minimum and maximum of the magnitude of the
measured impedance are at load angles
δ
= 0° and
δ
= 180°. If the measurement
location is the electrical centre, the measured voltage, and thus the measured
impedance, becomes zero when the load angle becomes
δ
= 180°.
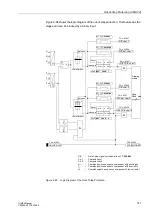
Power Swing
Polygon
The measurement characteristic is a rectangle with adjustable widths and inclination
angle
ϕ
P
. This ensures optimum matching to the conditions in the power station.
I(m)
I
U
G
U
N
–
Z
tot
----------------------
=
=
U(m)
U
G
m Z
tot
I
⋅
⋅
(
)
–
=
U
G
U
G
e
j
δ
G
⋅
=
U
N
U
N
e
j
δ
N
⋅
=
δ
δ
G
δ
N
–
=
Z(m)
1
1
U
N
U
G
--------
e
j
δ
–
⋅
è
ø
æ
ö
–
-------------------------------------
m
–
Z
tot
⋅
=