Zeiss LSM 880, Operating Manual

Page: 665 / 690

From equations (7) and (7a) it is evident that depth resolu-
tion varies linearly with the refractive index n of the immer-
sion liquid and with the square of the inverse value of the
numerical aperture of the objective lens {NA = n · sin(
α
)}.
To achieve high depth discrimination, it is important, above
all, to use objective lenses with the highest possible numeri-
cal aperture.
As an NA > 1 can only be obtained with an immersion liquid,
confocal fluorescence microscopy is usually performed with
immersion objectives (see also figure 11).
A comparison of the results stated before shows that axial
and lateral resolution in the limit case of PH=0 can be im-
proved by a factor of 1.4. Furthermore it should be noted
that, because of the wave-optical relationships discussed,
the optical performance of a confocal LSM cannot be en-
hanced infinitely. Equations (7) and (8) supply the minimum
possible slice thickness and the best possible resolution,
respectively.
15
From the applications point of view, the case of strictly
wave-optical confocality (PH=0) is irrelevant (see also Part 2).
By merely changing the factors in equations (7) and (8) it
is possible, though, to transfer the equations derived for
PH=0 to the pinhole diameter range up to 1 AU, to a good
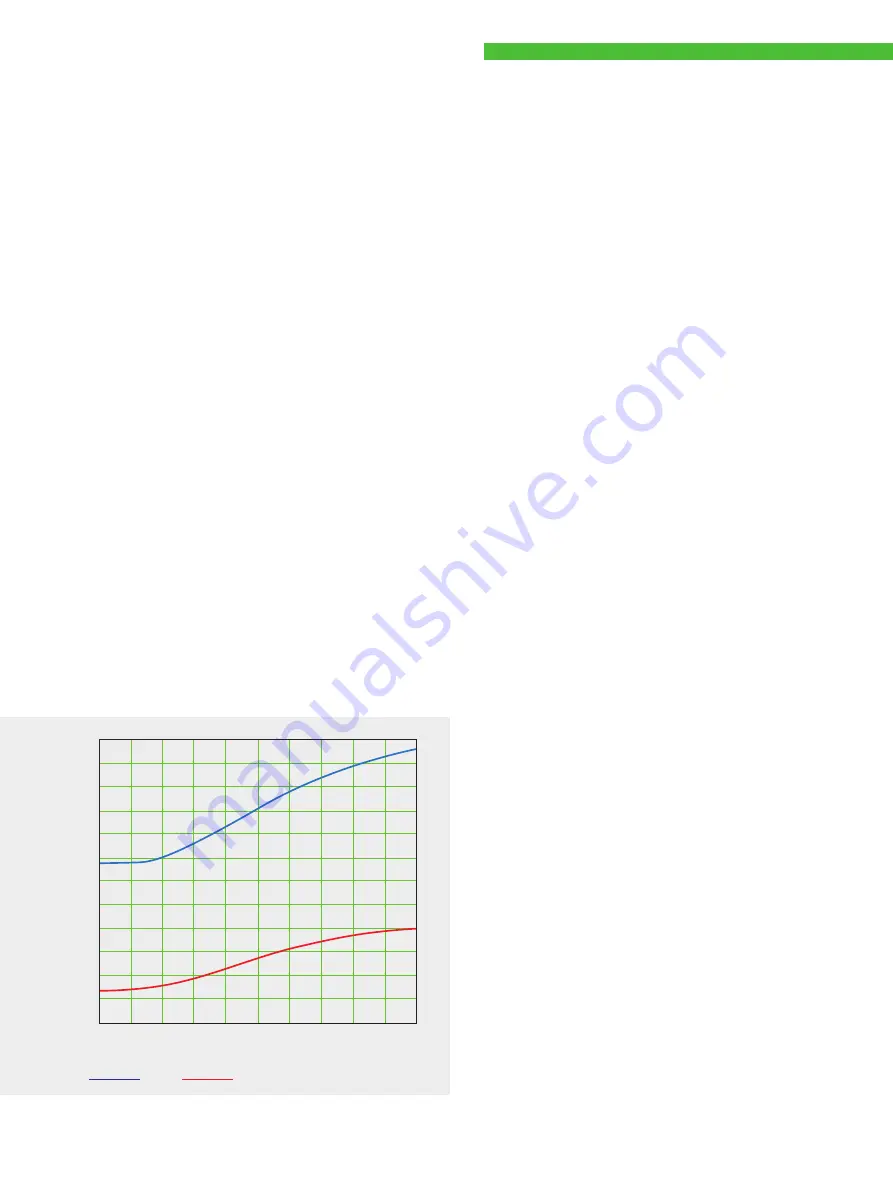
approximation. The factors applicable to particular pinhole
diameters can be taken from figure 10.
It must also be noted that with PH <1AU, a distinction be-
tween optical slice thickness and resolution can no longer
be made. The thickness of the optical slice at the same time
specifies the resolution properties of the system. That is why
in the literature the term of depth resolution is frequently
used as a synonym for depth discrimination or optical slice
thickness. However, this is only correct for pinhole diam-
eters smaller than 1 AU.
To conclude the observations about resolution and depth
discrimination (or depth resolution), the table on page 17
provides an overview of the formulary relationships devel-
oped in Part 1. In addition, figure 11a (page 16) shows
the overall curve of optical slice thickness for a microscope
objective of NA = 1.3 and n = 1.52 (
λ
 = 496 nm).
In figure 11 (b – d), equation (7) is plotted for different ob-
jects and varied parameters (NA,
λ
 , n).
Pinhole diameter [AU]
Factor
0.85
0.80
0.75
0.70
0.65
0.60
0.55
0.50
0.45
0.40
0.35
0.30
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
axial lateral
Fig. 10 Theoretical factors for equations (7) and (8),
with pinhole diameters between 0 and 1 AU.
OpticalImageFormation PART 1