Zeiss LSM 880, Руководство по эксплуатации

Страница: 215 / 690

CHAPTER 1 - SYSTEM OPERATION
LSM 880 Left Tool Area and Hardware Control Tools ZEISS
10/2014 V_01 000000-2071-464 209
D.2 Translational diffusion
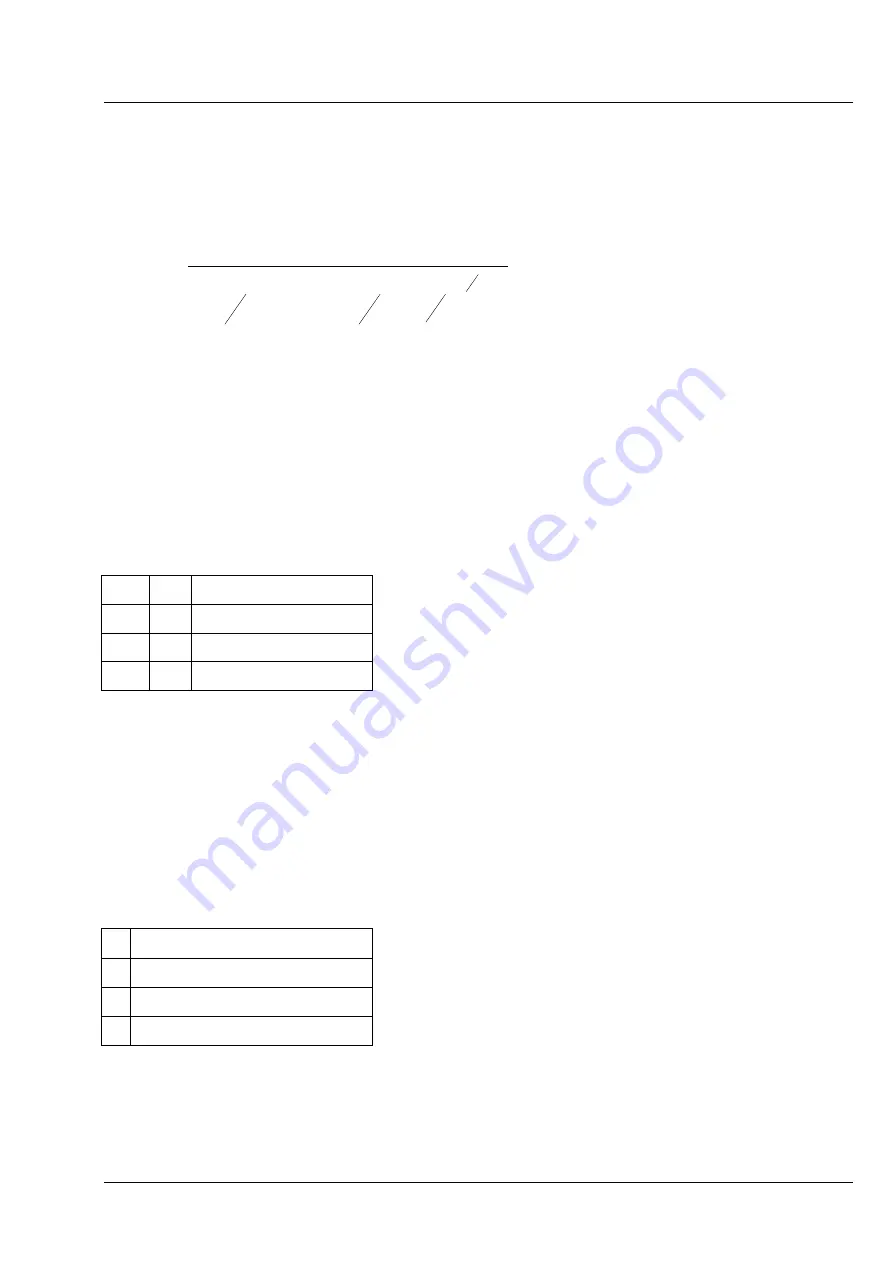
In its general form, translational diffusion is defined as:








































⋅






+ ⋅














+
Φ
=
∑
=
3
1
2
1
2
, ,
2
1
1
1 1
) (
i
e
i d
e
i d
i
d
d
i
d
i
S
G
α α
t
t
t
t
t
with the constraint
(8g)
with
t
d,i
representing the diffusional correlation time of molecule species i, S the structural parameter that
is the ratio of axial to lateral focus radii,
α
i
the anomaly parameter or temporal component of molecule
species I, e
d1
, e
d2
fixed exponentials to define dimensionality of diffusion (1-D: e
d1
=1/2; e
d2
=0; 2-D: e
d1
=1;
e
d2
=0; 3-D: e
d1
=1; e
d2
=1)
e
d1
and e
d2
are fixed values and have to be user defined. The following values define 1-, 2-and 3-D
diffusion:
e
d1
e
d2
dimensionality
1/2 0 1-D
1 0 2-D
1 1 3-D
Note that in the FCS software these values are automatically selected with the choice of dimensionality.
S is either a fit parameter or a fixed value. It is an instrumental parameter and can be determined by a
calibration experiment using a dye solution with a known diffusion as a fit result.
α
i
is either a fitted value for anomalous diffusion or a fixed value (set to "1") for free diffusion. The
following relation exists
α Diffusion process
=1 Free diffusion
<1 Anomalous sub-diffusion
>1 Anomalous super-diffusion
Note that
α
i
is set automatically to "1", if free diffusion is selected. If anomalous diffusion is selected, the
parameter will float.
1
= Φ
∑
i
i