manualshive.com logo in svg

Texas Instruments MSP430FR58 Series, Руководство пользователя


Поделиться
Скачать
background image

00

10

11

01

00

10

11

01

Correct State Transitions

Erroneous State Transitions

+1

1

Sensor B

(Signal PPUS2)

Sensor A

(Signal PPUS1)

A

B

A

A

A

A

B

B

B

B

A

B

Sensor A

(Signal PPUS1)

Sensor B

(Signal PPUS2)

Sensor B

(Signal PPUS2)

Sensor A

(Signal PPUS1)

90

45

01

11

10

00

01

11

10

Damping or “dark” area.

www.ti.com

ESI Operation

991

SLAU367P – October 2012 – Revised April 2020

Submit Documentation Feedback

Copyright © 2012–2020, Texas Instruments Incorporated

Extended Scan Interface (ESI)

37.2.8.3 Quadrature Decoding

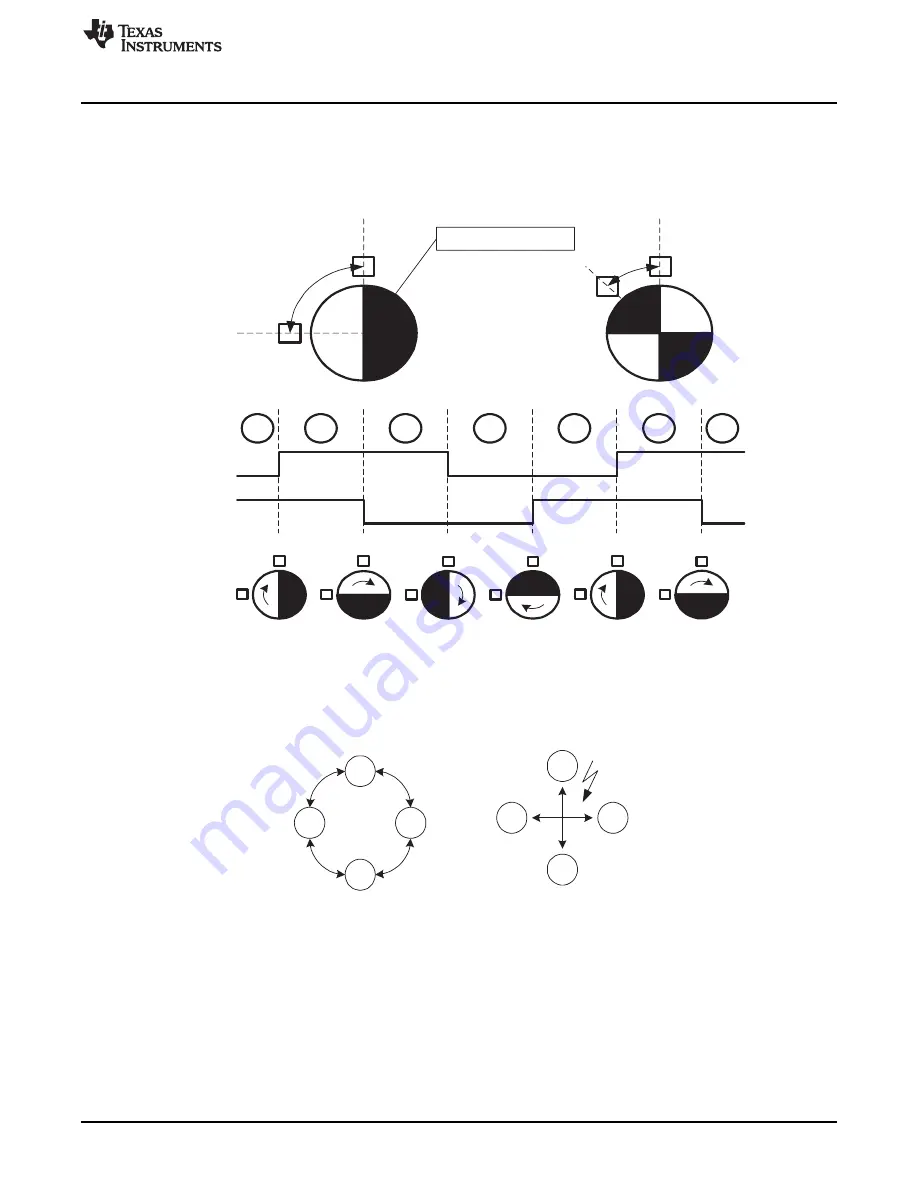
The ESI can be used to decode quadrature-encoded signals. Signals that are 90° out of phase with each
other are said to be in quadrature. To Create the signals, two sensors are positioned depending on the
slotting, or coating of the encoder disk.

Figure 37-20

shows two examples for the sensor positions and a

quadrature-encoded signal waveform.

Figure 37-20. Sensor Position and Quadrature Signals (S1=PPUS1, S2=PPUS2)

Quadrature decoding requires knowing the previous quadrature pair S1 (PPUS1) and S2 (PPUS2), as well
as the current pair. Comparing these two pairs will tell the direction of the rotation. For example, if the
current pair is 00 it can change to 01 or 10, depending on direction. Any other change in the signal pair
would represent an error as shown in

Figure 37-21

.

Figure 37-21. Quadrature Decoding State Diagram

To transfer the state encoding into counts it is necessary to decide what fraction of the rotation should be
counted and on what state transitions. In this example only full rotations will be counted on the transition
from state 00 to 01 or 10 using a 180° disk with the sensors 90° apart. All the possible state transitions
can be put into a table and this table can be translated into the corresponding state table entries for the
processing state machine as shown in

Table 37-8

.

Содержание MSP430FR58 Series

Страница 1: ...MSP430FR58xx MSP430FR59xx and MSP430FR6xx Family User s Guide Literature Number SLAU367P October 2012 Revised April 2020 ...

Страница 2: ... Low Power Modes LPM3 5 and LPM4 5 LPMx 5 59 1 5 Principles for Low Power Applications 61 1 6 Connection of Unused Pins 62 1 7 Reset Pin RST NMI Configuration 62 1 8 Configuring JTAG Pins 62 1 9 Vacant Memory Space 63 1 10 Boot Code 63 1 11 Bootloader BSL 63 1 12 JTAG Mailbox JMB System 63 1 12 1 JMB Configuration 64 1 12 2 JMBOUT0 and JMBOUT1 Outgoing Mailbox 64 1 12 3 JMBIN0 and JMBIN1 Incoming ...

Страница 3: ...tion 94 3 2 Clock System Operation 96 3 2 1 CS Module Features for Low Power Applications 96 3 2 2 LFXT Oscillator 96 3 2 3 HFXT Oscillator 97 3 2 4 Internal Very Low Power Low Frequency Oscillator VLO 98 3 2 5 Module Oscillator MODOSC 98 3 2 6 Digitally Controlled Oscillator DCO 98 3 2 7 Operation From Low Power Modes Requested by Peripheral Modules 99 3 2 8 CS Module Fail Safe Operation 100 3 2 ...

Страница 4: ...utting It All Together 280 5 2 6 Indirect Addressing of Result Registers 283 5 2 7 Using Interrupts 283 5 2 8 Using DMA 284 5 3 MPY32 Registers 285 5 3 1 MPY32CTL0 Register 287 6 FRAM Controller Overview 288 6 1 FRAM Controller Overview 288 7 FRAM Controller FRCTL 289 7 1 FRAM Introduction 290 7 2 FRAM Organization 290 7 3 FRCTL Module Operation 290 7 4 Programming FRAM Devices 291 7 4 1 Programmi...

Страница 5: ...319 9 6 2 IP Encapsulation Removal 320 9 7 MPU Registers 321 9 7 1 MPUCTL0 Register 322 9 7 2 MPUCTL1 Register 323 9 7 3 MPUSEGB2 Register 324 9 7 4 MPUSEGB1 Register 325 9 7 5 MPUSAM Register 326 9 7 6 MPUIPC0 Register 328 9 7 7 MPUIPSEGB2 Register 329 9 7 8 MPUIPSEGB1 Register 330 10 RAM Controller RAMCTL 331 10 1 RAM Controller RAMCTL Introduction 332 10 2 RAMCTL Operation 332 10 2 1 Considerat...

Страница 6: ...onfiguration 371 12 3 1 Configuration After Reset 371 12 3 2 Configuration of Unused Port Pins 372 12 3 3 Configuration for LPMx 5 Low Power Modes 372 12 4 Digital I O Registers 374 12 4 1 PxIV Register 388 12 4 2 PxIN Register 389 12 4 3 PxOUT Register 389 12 4 4 PxDIR Register 389 12 4 5 PxREN Register 390 12 4 6 PxSEL0 Register 390 12 4 7 PxSEL1 Register 390 12 4 8 PxSELC Register 391 12 4 9 Px...

Страница 7: ...ter 433 15 4 2 CRCDIRB Register 433 15 4 3 CRCINIRES Register 434 15 4 4 CRCRESR Register 434 16 CRC32 Module 435 16 1 Cyclic Redundancy Check CRC32 Module Introduction 436 16 2 CRC Checksum Generation 436 16 2 1 CRC Standard and Bit Order 437 16 2 2 CRC Implementation 437 16 2 3 Assembler Examples 437 16 3 CRC32 Register Descriptions 439 16 3 1 CRC32 Registers 439 17 Low Energy Accelerator LEA fo...

Страница 8: ...NFREQ Bit 481 20 3 3 PLL_LOCK Bit 481 20 3 4 USSXT Control Register 481 20 4 Start up Sequence of the USSXT Oscillator 481 20 4 1 USSXT Start up Behavior 482 20 5 Interrupts 482 20 6 HSPLL Registers 483 20 6 1 HSPLLIIDX Register Offset 0h reset 0h 484 20 6 2 HSPLLMIS Register Offset 2h reset 0h 485 20 6 3 HSPLLRIS Register Offset 4h reset 0h 486 20 6 4 HSPLLIMSC Register Offset 6h reset 0h 487 20 ...

Страница 9: ... Register Offset 22h reset 0h 531 21 8 15 SAPHCH0TT SAPH_ACH0TT Register Offset 24h reset 0h 532 21 8 16 SAPHCH1PUT SAPH_ACH1PUT Register Offset 26h reset 0h 533 21 8 17 SAPHCH1PDT SAPH_ACH1PDT Register Offset 28h reset 0h 534 21 8 18 SAPHCH1TT SAPH_ACH1TT Register Offset 2Ah reset 0h 535 21 8 19 SAPHMCNF SAPH_AMCNF Register Offset 2Ch reset 2h 536 21 8 20 SAPHTACTL SAPH_ATACTL Register Offset 2Eh...

Страница 10: ...95 22 5 1 SDHSIIDX Register Offset 0h reset 0h 596 22 5 2 SDHSMIS Register Offset 2h reset 0h 597 22 5 3 SDHSRIS Register Offset 4h reset 0h 598 22 5 4 SDHSIMSC Register Offset 6h reset 0h 600 22 5 5 SDHSICR Register Offset 8h reset 0h 601 22 5 6 SDHSISR Register Offset Ah reset 0h 602 22 5 7 SDHSDESCLO Register Offset Ch reset 110h 603 22 5 8 SDHSDESCHI Register Offset Eh reset BB10h 604 22 5 9 S...

Страница 11: ...tion 638 24 2 1 Watchdog Timer Counter WDTCNT 638 24 2 2 Watchdog Mode 638 24 2 3 Interval Timer Mode 638 24 2 4 Watchdog Timer Interrupts 638 24 2 5 Fail Safe Features 639 24 2 6 Operation in Low Power Modes 639 24 3 WDT_A Registers 640 24 3 1 WDTCTL Register 641 25 Timer_A 642 25 1 Timer_A Introduction 643 25 2 Timer_A Operation 645 25 2 1 16 Bit Timer Counter 645 25 2 2 Starting the Timer 645 2...

Страница 12: ...6 RTCSEC Register BCD Format 703 28 3 7 RTCMIN Register Hexadecimal Format 704 28 3 8 RTCMIN Register BCD Format 704 28 3 9 RTCHOUR Register Hexadecimal Format 705 28 3 10 RTCHOUR Register BCD Format 705 28 3 11 RTCDOW Register 706 28 3 12 RTCDAY Register Hexadecimal Format 706 28 3 13 RTCDAY Register BCD Format 706 28 3 14 RTCMON Register Hexadecimal Format 707 28 3 15 RTCMON Register BCD Format ...

Страница 13: ...al Format 744 29 4 14 RTCMIN Register Calendar Mode With BCD Format 744 29 4 15 RTCHOUR Register Calendar Mode With Hexadecimal Format 745 29 4 16 RTCHOUR Register Calendar Mode With BCD Format 745 29 4 17 RTCDOW Register Calendar Mode 746 29 4 18 RTCDAY Register Calendar Mode With Hexadecimal Format 746 29 4 19 RTCDAY Register Calendar Mode With BCD Format 746 29 4 20 RTCMON Register Calendar Mod...

Страница 14: ...g and Decoding 774 30 3 6 Automatic Error Detection 775 30 3 7 eUSCI_A Receive Enable 776 30 3 8 eUSCI_A Transmit Enable 776 30 3 9 UART Baud Rate Generation 777 30 3 10 Setting a Baud Rate 779 30 3 11 Transmit Bit Timing Error calculation 780 30 3 12 Receive Bit Timing Error Calculation 780 30 3 13 Typical Baud Rates and Errors 781 30 3 14 Using the eUSCI_A Module in UART Mode With Low Power Mode...

Страница 15: ...anced Universal Serial Communication Interface B eUSCI_B Overview 822 32 2 eUSCI_B Introduction I2 C Mode 822 32 3 eUSCI_B Operation I2 C Mode 823 32 3 1 eUSCI_B Initialization and Reset 824 32 3 2 I2 C Serial Data 824 32 3 3 I2 C Addressing Modes 825 32 3 4 I2 C Quick Setup 826 32 3 5 I2 C Module Operating Modes 827 32 3 6 Glitch Filtering 837 32 3 7 I2 C Clock Generation and Synchronization 837 ...

Страница 16: ...12_B Registers 887 34 3 1 ADC12CTL0 Register offset 00h reset 0000h 893 34 3 2 ADC12CTL1 Register offset 02h reset 0000h 895 34 3 3 ADC12CTL2 Register offset 04h reset 0020h 897 34 3 4 ADC12CTL3 Register offset 06h reset 0000h 898 34 3 5 ADC12MEMx Register x 0 to 31 899 34 3 6 ADC12MCTLx Register x 0 to 31 900 34 3 7 ADC12HI Register offset 0Ah reset 0FFFh 902 34 3 8 ADC12LO Register offset 08h re...

Страница 17: ...ux Mode 945 36 2 11 4 Mux Mode 946 36 2 12 6 Mux Mode 947 36 2 13 8 Mux Mode 948 36 3 LCD_C Registers 950 36 3 1 LCDCCTL0 Register 955 36 3 2 LCDCCTL1 Register 957 36 3 3 LCDCBLKCTL Register 958 36 3 4 LCDCMEMCTL Register 959 36 3 5 LCDCVCTL Register 960 36 3 6 LCDCPCTL0 Register 962 36 3 7 LCDCPCTL1 Register 962 36 3 8 LCDCPCTL2 Register 963 36 3 9 LCDCPCTL3 Register 963 36 3 10 LCDCCPCTL Registe...

Страница 18: ...ESICTL Register 1010 37 3 19 ESITHR1 Register 1012 37 3 20 ESITHR2 Register 1012 37 3 21 ESIDAC1Rx Register x 0 to 7 1013 37 3 22 ESIDAC2Rx Register x 0 to 7 1013 37 3 23 ESITSMx Register x 0 to 31 1014 37 3 24 Extended Scan Interface Processing State Machine Table Entry ESI Memory 1016 38 Embedded Emulation Module EEM 1017 38 1 Embedded Emulation Module EEM Introduction 1018 38 2 EEM Building Blo...

Страница 19: ...Block Diagram 84 2 2 Voltage Failure and Resulting PMM Actions 85 2 3 PMM Action at Device Power Up 86 2 4 PMMCTL0 Register 89 2 5 PMMCTL1 Register 90 2 6 PMMIFG Register 91 2 7 PM5CTL0 Register 92 3 1 Clock System Block Diagram 95 3 2 Module Request Clock System 99 3 3 Oscillator Fault Logic 101 3 4 Switch MCLK From DCOCLK to LFXTCLK 102 3 5 CTL0 Register 104 3 6 CTL1 Register 105 3 7 CTL2 Regist...

Страница 20: ...n Format 151 4 33 RRCM RRAM RRUM and RLAM Instruction Format 151 4 34 BRA Instruction Format 151 4 35 CALLA Instruction Format 151 4 36 Decrement Overlap 177 4 37 Stack After a RET Instruction 196 4 38 Destination Operand Arithmetic Shift Left 198 4 39 Destination Operand Carry Left Shift 199 4 40 Rotate Right Arithmetically RRA B and RRA W 200 4 41 Rotate Right Through Carry RRC B and RRC W 201 4...

Страница 21: ...Example of Segment Border Register Fixed Bits When FRAM Size 256KB 313 9 5 Segmentation of Main Memory 314 9 6 IP Encapsulation Access Rights Equivalent Schematic 315 9 7 MPUCTL0 Register 322 9 8 MPUCTL1 Register 323 9 9 MPUSEGB2 Register 324 9 10 MPUSEGB1 Register 325 9 11 MPUSAM Register 326 9 12 MPUIPC0 Register 328 9 13 MPUIPSEGB2 Register 329 9 14 MPUIPSEGB1 Register 330 10 1 RAM Power Mode T...

Страница 22: ...ption 409 14 8 CBC Encryption 410 14 9 CBC Decryption 411 14 10 OFB Encryption 413 14 11 OFB Decryption 414 14 12 CFB Encryption 415 14 13 CFB Decryption 416 14 14 AESACTL0 Register 418 14 15 AESACTL1 Register 420 14 16 AESASTAT Register 421 14 17 AESAKEY Register 422 14 18 AESADIN Register 423 14 19 AESADOUT Register 424 14 20 AESAXDIN Register 425 14 21 AESAXIN Register 426 15 1 LFSR Implementat...

Страница 23: ...0 4 HSPLLMIS Register 485 20 5 HSPLLRIS Register 486 20 6 HSPLLIMSC Register 487 20 7 HSPLLICR Register 488 20 8 HSPLLISR Register 489 20 9 HSPLLDESCLO Register 490 20 10 HSPLLDESCHI Register 491 20 11 HSPLLCTL Register 492 20 12 HSPLLUSSXTLCTL Register 494 21 1 USS or USS_A Block Diagram 497 21 2 PPG or PPG_A Block Diagram 497 21 3 PPG or PPG_A Internal State Diagrams for Single Tone 498 21 4 PPG...

Страница 24: ...ACH1PDT Register 534 21 38 SAPHCH1TT SAPH_ACH1TT Register 535 21 39 SAPHMCNF SAPH_AMCNF Register 536 21 40 SAPHTACTL SAPH_ATACTL Register 537 21 41 SAPHICTL0 SAPH_AICTL0 Register 538 21 42 SAPHBCTL SAPH_ABCTL Register 540 21 43 SAPHPGC SAPH_APGC Register 542 21 44 SAPHPGLPER SAPH_APGLPER Register 543 21 45 SAPHPGHPER SAPH_APGHPER Register 544 21 46 SAPHPGCTL SAPH_APGCTL Register 545 21 47 SAPHPPGT...

Страница 25: ...ment SDHSCTL0 TRGSRC 1 584 22 19 Example Using SDHSCTL3 TRIGEN Bit SDHSCTL0 AUTOSSDIS 0 586 22 20 Example Using SDSCTL3 TRIGEN bit SDHSCTL0 AUTOSSDIS 1 587 22 21 Conversion Start and Stop When SDHSCTL0 AUTOSSDIS 0 588 22 22 Conversion Start and Stop When SDHSCTL0 AUTOSSDIS 1 589 22 23 First Interrupt Position With SDHSCTL0 INTDLY 2 589 22 24 SDHSCTL0 AUTOSSDIS 0 SDHSCTL2 SMPCTLOFF 0 SDHSCTL0 INTDL...

Страница 26: ...p Down Mode 648 25 8 Up Down Mode Flag Setting 648 25 9 Output Unit in Up Down Mode 649 25 10 Capture Signal SCS 1 650 25 11 Capture Cycle 650 25 12 Output Example Timer in Up Mode 652 25 13 Output Example Timer in Continuous Mode 653 25 14 Output Example Timer in Up Down Mode 654 25 15 Capture Compare Interrupt Flag 655 25 16 TAxCTL Register 658 25 17 TAxR Register 659 25 18 TAxCCTLn Register 660...

Страница 27: ...ister 706 28 14 RTCDAY Register 706 28 15 RTCMON Register 707 28 16 RTCMON Register 707 28 17 RTCYEAR Register 708 28 18 RTCYEAR Register 708 28 19 RTCAMIN Register 709 28 20 RTCAMIN Register 709 28 21 RTCAHOUR Register 710 28 22 RTCAHOUR Register 710 28 23 RTCADOW Register 711 28 24 RTCADAY Register 712 28 25 RTCADAY Register 712 28 26 RTCPS0CTL Register 713 28 27 RTCPS1CTL Register 714 28 28 RTC...

Страница 28: ...ter 750 29 31 RTCADOW Register 751 29 32 RTCADAY Register 752 29 33 RTCADAY Register 752 29 34 RTCPS0CTL Register 753 29 35 RTCPS1CTL Register 754 29 36 RTCPS0 Register 756 29 37 RTCPS1 Register 756 29 38 RTCIV Register 757 29 39 BIN2BCD Register 758 29 40 BCD2BIN Register 758 29 41 RTCSECBAKx Register 759 29 42 RTCSECBAKx Register 759 29 43 RTCMINBAKx Register 760 29 44 RTCMINBAKx Register 760 29...

Страница 29: ...CI Block Diagram SPI Mode 799 31 2 eUSCI Master and External Slave UCSTEM 0 801 31 3 eUSCI Slave and External Master 802 31 4 eUSCI SPI Timing With UCMSB 1 804 31 5 UCAxCTLW0 Register 807 31 6 UCAxBRW Register 808 31 7 UCAxSTATW Register 809 31 8 UCAxRXBUF Register 810 31 9 UCAxTXBUF Register 811 31 10 UCAxIE Register 812 31 11 UCAxIFG Register 813 31 12 UCAxIV Register 814 31 13 UCBxCTLW0 Registe...

Страница 30: ... 858 32 33 UCBxIV Register 860 33 1 REF_A Block Diagram 862 33 2 REFCTL0 Register 866 34 1 ADC12_B Block Diagram 870 34 2 Analog Multiplexer T Switch 872 34 3 Extended Sample Mode Without Internal Reference in 12 Bit Mode 874 34 4 Extended Sample Mode With Internal Reference in 12 Bit Mode 874 34 5 Pulse Sample Mode First Conversion or Where ADC12MSC 0 in 12 Bit Mode 875 34 6 Pulse Sample Mode Sub...

Страница 31: ... LCD Memory for 5 Mux to 8 Mux Mode Example for 160 Segments 935 36 4 Bias Generation 938 36 5 Example Static Waveforms 943 36 6 Example 2 Mux Waveforms 944 36 7 Example 3 Mux Waveforms 945 36 8 Example 4 Mux Waveforms 946 36 9 Example 6 Mux Waveforms 947 36 10 Example 8 Mux 1 3 Bias Waveforms LCDLP 0 948 36 11 Example 8 Mux 1 3 Bias Low Power Waveforms LCDLP 1 949 36 12 LCDCCTL0 Register 955 36 1...

Страница 32: ... PPUS1 S2 PPUS2 991 37 21 Quadrature Decoding State Diagram 991 37 22 ESIDEBUG1 Register 994 37 23 ESIDEBUG2 Register 994 37 24 ESIDEBUG3 Register 994 37 25 ESIDEBUG4 Register 995 37 26 ESIDEBUG5 Register 995 37 27 ESICNT0 Register 996 37 28 ESICNT1 Register 996 37 29 ESICNT2 Register 997 37 30 ESICNT3 Register 997 37 31 ESIIV Register 998 37 32 ESIINT1 Register 999 37 33 ESIINT2 Register 1001 37 ...

Страница 33: ... Register Description 80 1 22 SYSJMBO1 Register Description 80 1 23 SYSUNIV Register Description 81 1 24 SYSSNIV Register Description 81 1 25 SYSRSTIV Register Description 82 2 1 PMM Registers 88 2 2 PMMCTL0 Register Description 89 2 3 PMMCTL1 Register Description 90 2 4 PMMIFG Register Description 91 2 5 PM5CTL0 Register Description 92 3 1 HFFREQ Settings 97 3 2 System Clocks Power Modes and Cloc...

Страница 34: ... Availability in Fractional Mode MPYFRAC 1 MPYSAT 0 278 5 6 Result Availability in Saturation Mode MPYSAT 1 279 5 7 MPY32 Registers 285 5 8 Alternative Registers 286 5 9 MPY32CTL0 Register Description 287 6 1 FRAM Controller Overview 288 7 1 FRCTL Registers 294 7 2 FRCTL0 Register Description 295 7 3 GCCTL0 Register Description 296 7 4 GCCTL1 Register Description 297 8 1 FRAM memory Access Speed 3...

Страница 35: ... PxOUT Register Description 389 12 7 P1DIR Register Description 389 12 8 PxREN Register Description 390 12 9 PxSEL0 Register Description 390 12 10 PxSEL1 Register Description 390 12 11 PxSELC Register Description 391 12 12 PxIES Register Description 391 12 13 PxIE Register Description 391 12 14 PxIFG Register Description 392 13 1 CapTouch Registers 396 13 2 CAPTIOxCTL Register Description 397 14 1...

Страница 36: ...escription 445 17 1 LEA Command Groups 448 17 2 DSP Library and MSPWare Versions for the LEA 449 18 1 Auto Mode and Register Mode 454 18 2 Time Mark Events 454 18 3 USS_PWRREQ Signal Source 455 18 4 Control Signals Among USS Submodules 456 19 1 USS Power State 461 19 2 USS Power States and State Changes 462 19 3 Device Power Modes and USS Power States 463 19 4 Internal Control Signals 463 19 5 ASQ...

Страница 37: ...ACH0PDT Register Field Descriptions 531 21 20 SAPHCH0TT SAPH_ACH0TT Register Field Descriptions 532 21 21 SAPHCH1PUT SAPH_ACH1PUT Register Field Descriptions 533 21 22 SAPHCH1PDT SAPH_ACH1PDT Register Field Descriptions 534 21 23 SAPHCH1TT SAPH_ACH1TT Register Field Descriptions 535 21 24 SAPHMCNF SAPH_AMCNF Register Field Descriptions 536 21 25 SAPHTACTL SAPH_ATACTL Register Field Descriptions 53...

Страница 38: ...scriptions 598 22 15 SDHSIMSC Register Field Descriptions 600 22 16 SDHSICR Register Field Descriptions 601 22 17 SDHSISR Register Field Descriptions 602 22 18 SDHSDESCLO Register Field Descriptions 603 22 19 SDHSDESCHI Register Field Descriptions 604 22 20 SDHSCTL0 Register Field Descriptions 605 22 21 SDHSCTL1 Register Field Descriptions 607 22 22 SDHSCTL2 Register Field Descriptions 608 22 23 S...

Страница 39: ...684 26 9 TBxCCRn Register Description 686 26 10 TBxIV Register Description 687 26 11 TBxEX0 Register Description 688 27 1 RTC Overview 689 28 1 RTC_B Registers 698 28 2 RTCCTL0 Register Description 700 28 3 RTCCTL1 Register Description 701 28 4 RTCCTL2 Register Description 702 28 5 RTCCTL3 Register Description 702 28 6 RTCSEC Register Description 703 28 7 RTCSEC Register Description 703 28 8 RTCMI...

Страница 40: ...ion 742 29 13 RTCNT3 Register Description 742 29 14 RTCNT4 Register Description 742 29 15 RTCSEC Register Description 743 29 16 RTCSEC Register Description 743 29 17 RTCMIN Register Description 744 29 18 RTCMIN Register Description 744 29 19 RTCHOUR Register Description 745 29 20 RTCHOUR Register Description 745 29 21 RTCDOW Register Description 746 29 22 RTCDAY Register Description 746 29 23 RTCD...

Страница 41: ...mended Settings for Typical Crystals and Baud Rates 782 30 6 UART State Change Interrupt Flags 784 30 7 eUSCI_A UART Registers 786 30 8 UCAxCTLW0 Register Description 787 30 9 UCAxCTLW1 Register Description 788 30 10 UCAxBRW Register Description 789 30 11 UCAxMCTLW Register Description 789 30 12 UCAxSTATW Register Description 790 30 13 UCAxRXBUF Register Description 791 30 14 UCAxTXBUF Register De...

Страница 42: ... Register Description 855 32 17 UCBxI2CSA Register Description 855 32 18 UCBxIE Register Description 856 32 19 UCBxIFG Register Description 858 32 20 UCBxIV Register Description 860 33 1 REF_A Registers 865 33 2 REFCTL0 Register Description 866 34 1 ADC12_B Conversion Result Formats 876 34 2 Conversion Mode Summary 877 34 3 ADC12_B Registers 887 34 4 ADC12CTL0 Register Description 893 34 5 ADC12CT...

Страница 43: ...CPCTL Register Description 964 36 18 LCDCIV Register Description 964 37 1 ESICAX and ESISH Input Selection 971 37 2 Selected Output Bits 972 37 3 Selected DAC Registers 973 37 4 DAC Register Select When TESTDX 1 974 37 5 TSM State Duration 977 37 6 TSM Example Register Values 978 37 7 ESI Interrupts 985 37 8 Quadrature Decoding PSM Table 992 37 9 ESI Registers 993 37 10 ESIDEBUG1 Register Descript...

Страница 44: ...struments Incorporated List of Tables 37 30 ESITHR2 Register Description 1012 37 31 ESIDAC1Rx Register Description 1013 37 32 ESIDAC2Rx Register Description 1013 37 33 ESITSMx Register Description 1014 37 34 Extended Scan Interface Processing State Machine Table Entry Description 1016 38 1 EEM Configurations 1022 ...

Страница 45: ...specific data sheet for these details Related Documentation From Texas Instruments For related documentation visit the MSP430 web site at http www ti com msp430 Notational Conventions Program examples are shown in a special typeface for example MOV 255 R10 XOR R5 R6 Glossary Abbreviation Description ACLK Auxiliary clock ADC Analog to digital converter BOR Brownout reset BSL Bootloader see www ti c...

Страница 46: ...z16 16 bit address space Register Bit Conventions Each register is shown with a key indicating the accessibility of the each individual bit and the initial condition Register Bit Accessibility and Initial Condition Key Bit Accessibility rw Read write r Read only r0 Read as 0 r1 Read as 1 w Write only w0 Write as 0 w1 Write as 1 w No register bit implemented writing a 1 results in a pulse The regis...

Страница 47: ...urce selection and management User data exchange mechanism through the JTAG mailbox JMB Bootloader BSL entry mechanism Configuration management device descriptors Interrupt vector generators for reset and NMIs Topic Page 1 1 System Control Module SYS Introduction 48 1 2 System Reset and Initialization 48 1 3 Interrupts 50 1 4 Operating Modes 56 1 5 Principles for Low Power Applications 61 1 6 Conn...

Страница 48: ... mode Wake up event from LPMx 5 that is LPM3 5 or LPM4 5 mode SVSH low condition when enabled see the PMM and SVS chapter for details Software BOR event see the PMM and SVS chapter for details A POR is always generated when a BOR is generated but a BOR is not generated by a POR The following events trigger a POR BOR signal Software POR event see the PMM and SVS chapter for details A PUC is always ...

Страница 49: ...dog Timer s EN from port wakeup logic s PUC Logic Module PUCs MCLK notRST Delay clr clr clr www ti com System Reset and Initialization 49 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated System Resets Interrupts and Operating Modes System Control Module SYS Figure 1 1 BOR POR and PUC Reset Circuit ...

Страница 50: ...ddress See Section 1 10 for more information regarding the boot code Upon completion of the boot code the PC is loaded with the address contained at the SYSRSTIV reset location 0FFFEh After a system reset user software must initialize the device for the application requirements The following must occur Initialize the stack pointer SP typically to the top of RAM when available otherwise FRAM locati...

Страница 51: ...am for NMI sources is shown in Section 1 3 A UNMI interrupt can be generated by following sources An edge on the RST NMI pin when configured in NMI mode An oscillator fault occurs A SNMI interrupt can be generated by following sources FRAM errors see the FRAM Controller chapter for details Vacant memory access JTAG mailbox JMB event NOTE The number and types of NMI sources may vary from device to ...

Страница 52: ...errupt request flag resets automatically on single source flags Multiple source flags remain set for servicing by software 6 All bits of SR are cleared except SCG0 thereby terminating any low power mode Because the GIE bit is cleared further interrupts are disabled 7 The content of the interrupt vector is loaded into the PC the program continues with the interrupt service routine at that address F...

Страница 53: ...esting Interrupt nesting is enabled if the GIE bit is set inside an interrupt service routine When interrupt nesting is enabled any interrupt occurring during an interrupt service routine interrupts the routine regardless of the interrupt priorities 1 3 6 Interrupt Vectors The interrupt vectors are located in the address range 0FFFFh to 0FF80h for a maximum of 64 interrupt sources A vector is prog...

Страница 54: ...te that the SYSRIVECT bit is automatically cleared on a BOR so the default reset vector location 0FFFEh will be used after a BOR before setting the SYSRIVECT bit to 1 1 3 7 SYS Interrupt Vector Generators SYS collects all system NMI SNMI sources user NMI UNMI sources and BOR POR or PUC reset sources of all the other modules They are combined into three interrupt vectors The interrupt vector regist...

Страница 55: ...tor 0 No interrupt JMP DBD_ISR Vector 2 DBDIFG JMP ACCTIM_ISR Vector 4 ACCTIMIFG JMP RSVD1_ISR Vector 6 Reserved for future usage JMP RSVD2_ISR Vector 8 Reserved for future usage JMP RSVD3_ISR Vector 10 Reserved for future usage JMP RSVD4_ISR Vector 12 Reserved for future usage JMP ACCV_ISR Vector 14 ACCVIFG JMP VMA_ISR Vector 16 VMAIFG JMP JMBI_ISR Vector 18 JMBINIFG JMP JMBO_ISR Vector 20 JMBOUT...

Страница 56: ... takes effect immediately Peripherals operating with any disabled clock are disabled until the clock becomes active Peripherals may also be disabled with their individual control register settings All I O port pins RAM and registers are unchanged Wakeup from LPM0 through LPM4 is possible through all enabled interrupts When LPMx 5 LPM3 5 or LPM4 5 is entered the voltage regulator of the Power Manag...

Страница 57: ... VCORE CPUOFF 1 OSCOFF 0 SCG0 0 SCG1 0 CPUOFF 1 OSCOFF 0 SCG0 1 SCG1 0 CPUOFF 1 OSCOFF 0 SCG0 0 SCG1 1 CPUOFF 1 OSCOFF 0 SCG0 1 SCG1 1 CPUOFF 1 OSCOFF 1 SCG0 1 SCG1 1 PMMREGOFF 1 PMM WDT CS FRAM Password violation to LPMx 5 From active mode Events Operating modes Reset phases Arbitrary transitions Any enabled interrupt and NMI performs this transition An enabled reset always restarts the device RS...

Страница 58: ... DCO is enabled or DCO sources MCLK or SMCLK SMCLKOFF 0 1 0 0 1 LPM2 CPU MCLK are disabled ACLK is active SMCLK is disabled 1 1 0 1 LPM3 CPU MCLK are disabled ACLK is active SMCLK is disabled 1 1 1 1 LPM4 CPU and all clocks are disabled 1 1 1 1 LPM3 5 When PMMREGOFF 1 regulator is disabled No memory retention In this mode RTC operation is possible when configured properly See the RTC module for fu...

Страница 59: ...LPM3 Interrupt Service Routine BIC CPUOFF SCG1 SCG0 0 SP Exit LPM3 on RETI RETI Enter LPM4 Example BIS GIE CPUOFF OSCOFF SCG1 SCG0 SR Enter LPM4 Program stops here Exit LPM4 Interrupt Service Routine BIC CPUOFF OSCOFF SCG1 SCG0 0 SP Exit LPM4 on RETI RETI 1 4 3 Low Power Modes LPM3 5 and LPM4 5 LPMx 5 The low power modes LPM3 5 and LPM4 5 LPMx 5 1 give the lowest power consumption on a device In L...

Страница 60: ...e enabled if necessary Only modules connected to the RTC LDO can stay active 6 For LPM3 5 if necessary enable any interrupt sources from these modules as wakeup sources Refer to the corresponding module chapter 7 Disable the watchdog timer WDT if it is enabled and in watchdog mode If the WDT is enabled and in watchdog mode the device does not enter LPMx 5 8 Clear the GIE bit BIC GIE SR 9 Do the fo...

Страница 61: ... A wakeup event on an I O if configured and enabled The interrupt flag of the corresponding port pin is set PxIFG The PMMLPM5IFG bit is set A wakeup from the RST pin A power cycle Either the SVSHIFG or none of the PMMIFGs is set Any exit from LPM4 5 causes a BOR The program execution starts at the address the reset vector points to PMMLPM5IFG 1 indicates a wakeup from LPM4 5 or the System Reset Ve...

Страница 62: ...NMI function through the Special Function Register SFR SFRRPCR Setting SYSNMI causes the RST NMI pin to be configured as an external NMI source The external NMI is edge sensitive and its edge is selectable by SYSNMIIES Setting the NMIIE enables the interrupt of the external NMI Upon an external NMI event the NMIIFG is set The RST NMI pin can have either a pullup or pulldown present or not SYSRSTUP...

Страница 63: ...uses SYSBSLIND to be set An added sequence of commands initiates the desired function A bootloader session can be exited by continuing operation at a defined user program address or by applying the standard reset sequence Access to the device memory through the BSL is protected against misuse by a user defined password Two BSL signatures BSL Signature 1 memory location 0FF84h and BSL Signature 2 m...

Страница 64: ...leared by software 1 12 4 JMB NMI Usage The JMB handshake mechanism can be configured to use interrupts to avoid unnecessary polling if desired In 16 bit mode JMBOUTIFG is set when JMBOUT0 has been read by the JTAG port and is ready to receive data In 32 bit mode JMBOUTIFG is set when both JMBOUT0 and JMBOUT1 has been read by the JTAG port and are ready to receive data If JMBOUTIE is set these eve...

Страница 65: ...Signature 2 The starting location of the password is fixed at location 0FF88h As an example for a password of length 4 the password memory locations would reside at 0FF88h 0FF8Ah 0FF8Ch and 0FF8Eh The password is not checked after each BOR it is checked only if a specific signature is present in the JTAG incoming mailbox If the JTAG incoming mailbox contains 0A55Ah and 01E1Eh in JMBIN0 and JMBIN1 ...

Страница 66: ...Device Type The value read at address 00FF0h identifies the family branch of the device All values starting with 80h indicate a hierarchical structure consisting of the information block and a TLV tag length value TLV structure containing the various descriptors Any other value than 80h read at address location 00FF0h indicates the device is of an older family and contains a flat descriptor beginn...

Страница 67: ...bration see Section 1 14 3 2 and Section 1 14 3 3 REFCAL 12h REF calibration see Section 1 14 3 1 ADC10CAL 13h ADC10 calibration see Section 1 14 3 2 and Section 1 14 3 3 Reserved 14h Reserved for future use RANDTAG 15h Random Number Seed see Section 1 14 3 4 Reserved 16h 1Bh Reserved for future use BSLTAG 1Ch BSL Configuration Reserved 1Dh FDh Reserved for future use TAGEXT FEh Tag extender Each ...

Страница 68: ...OR High Byte Low Byte CAL_ADC_25VREF_FACTOR High Byte The calibration data for the REF module consists of three words one word for each reference voltage available 1 2 V 2 0 V and 2 5 V The reference voltages are measured at room temperature The measured values are normalized by 1 2 V 2 0 V or 2 5 V before being stored into the TLV structure as shown in Equation 2 2 In this way a conversion result...

Страница 69: ...at room temperature is determined and stored as a twos complement number in the TLV structure The offset error correction is done by adding the CAL_ADC_OFFSET to the conversion result 4 The gain of the ADC at room temperature with an external reference voltage of 2 5 V is calculated by Equation 5 5 The conversion result is gain corrected by multiplying it with the CAL_ADC_GAIN_FACTOR and dividing ...

Страница 70: ...s programmed during test of the device It is generated on the test system using a cryptographic random number generator 1 14 3 5 BSL Configuration Table 1 9 shows the tags used for the BSL configuration The BSL configuration stores the communication interface selection and corresponding communication interface settings The Tag is optional for devices only providing the basic UART BSL interface The...

Страница 71: ...ield Depending on the selected communication interface the subsequent bytes in the BSL config tag are interpreted to configure the communication interface The interpretation is shown in Table 1 11 Unused bytes in BSL_CIF_CONFIG are defined as 00h Table 1 11 BSL_CIF_CONFIG Values BSL_CIF_CONFIG_IF n UART BSL_COM_IF 00h I2C BSL_COM_IF 01h 0 00h I2C address valid values 0 to 7Fh 1 to FFh N A N A Tabl...

Страница 72: ...egisters have word or byte register access For a generic register ANYREG the suffix _L ANYREG_L refers to the lower byte of the register bits 0 through 7 The suffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 Table 1 12 SFR Registers Offset Acronym Register Name Type Access Reset Section 00h SFRIE1 Interrupt Enable Read write Word 0000h Section 1 15 1 00h SFRIE1_L IE1 Re...

Страница 73: ...t interrupt enable 0b Interrupts disabled 1b Interrupts enabled 6 JMBINIE RW 0h JTAG mailbox input interrupt enable 0b Interrupts disabled 1b Interrupts enabled 5 Reserved R 0h Reserved Always reads as 0 4 NMIIE RW 0h NMI pin interrupt enable 0b Interrupts disabled 1b Interrupts enabled 3 VMAIE RW 0h Vacant memory access interrupt enable 0b Interrupts disabled 1b Interrupts enabled 2 Reserved R 0h...

Страница 74: ... been received by the JTAG module and are ready for new messages from the CPU 6 JMBINIFG RW 0h JTAG mailbox input interrupt flag 0b No interrupt pending When in 16 bit mode JMBMODE 0 this bit is cleared automatically when JMBI0 is read by the CPU When in 32 bit mode JMBMODE 1 this bit is cleared automatically when both JMBI0 and JMBI1 have been read by the CPU This bit is also cleared when the ass...

Страница 75: ...ritten as 1 Table 1 15 SFRRPCR Register Description Bit Field Type Reset Description 15 5 Reserved R 0h Reserved Always reads as 0 4 Reserved R W 1 1h Reserved Must be written as 1 3 SYSRSTRE RW 1h Reset pin resistor enable 0b Pullup or pulldown resistor at the RST NMI pin is disabled 1b Pullup or pulldown resistor at the RST NMI pin is enabled 2 SYSRSTUP RW 1h Reset resistor pin pullup or pulldow...

Страница 76: ...Section 00h SYSCTL System Control Read write Word 0000h Section 1 16 1 00h SYSCTL_L Read write Byte 00h 01h SYSCTL_H Read write Byte 00h 06h SYSJMBC JTAG Mailbox Control Read write Word 000Ch Section 1 16 2 06h SYSJMBC_L Read write Byte 0Ch 07h SYSJMBC_H Read write Byte 00h 08h SYSJMBI0 JTAG Mailbox Input 0 Read write Word 0000h Section 1 16 3 08h SYSJMBI0_L Read write Byte 00h 09h SYSJMBI0_H Read...

Страница 77: ...sequence detected 1b BSL entry sequence detected 3 Reserved R 0h Reserved Always reads as 0 2 SYSPMMPE RW 0h PMM access protect This controls the accessibility of the PMM control registers Once set to 1 it only can be cleared by a BOR 0b Access from anywhere in memory 1b Access only from the BSL segments 1 Reserved R 0h Reserved Always reads as 0 0 SYSRIVECT RW 0h RAM based interrupt vectors 0b In...

Страница 78: ...s using JMBO0 and JMBI0 only 1b 32 bit transfers using JMBO0 with JMBO1 and JMBI0 with JMBI1 3 JMBOUT1FG R 1h Outgoing JTAG Mailbox 1 flag This bit is cleared automatically when a message is written to the upper byte of JMBO1 or as word access by the CPU DMA and is set after the message was read through JTAG 0b JMBO1 is not ready to receive new data 1b JMBO1 is ready to receive new data 2 JMBOUT0F...

Страница 79: ... rw 0 rw 0 rw 0 rw 0 rw 0 Table 1 19 SYSJMBI0 Register Description Bit Field Type Reset Description 15 8 MSGHI RW 0h JTAG mailbox incoming message high byte 7 0 MSGLO RW 0h JTAG mailbox incoming message low byte 1 16 4 SYSJMBI1 Register JTAG Mailbox Input 1 Register Figure 1 13 SYSJMBI1 Register 15 14 13 12 11 10 9 8 MSGHI rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 MSGLO rw 0 rw 0 rw ...

Страница 80: ... rw 0 rw 0 rw 0 rw 0 rw 0 Table 1 21 SYSJMBO0 Register Description Bit Field Type Reset Description 15 8 MSGHI RW 0h JTAG mailbox outgoing message high byte 7 0 MSGLO RW 0h JTAG mailbox outgoing message low byte 1 16 6 SYSJMBO1 Register JTAG Mailbox Output 1 Register Figure 1 15 SYSJMBO1 Register 15 14 13 12 11 10 9 8 MSGHI rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 MSGLO rw 0 rw 0 rw...

Страница 81: ...erates a value that can be used as address offset for fast interrupt service routine handling Writing to this register clears all pending user NMI flags See the device specific data sheet for a list of values 1 16 8 SYSSNIV Register System NMI Vector Register Figure 1 17 SYSSNIV Register 15 14 13 12 11 10 9 8 SYSSNIV r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 SYSSNIV r0 r0 r0 r 0 r 0 r 0 r 0 r0 Table...

Страница 82: ...ister 15 14 13 12 11 10 9 8 SYSRSTIV r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 SYSRSTIV r0 r0 r 1 r 1 r 1 r 1 r 1 r0 1 Reset value depends on reset source Table 1 25 SYSRSTIV Register Description Bit Field Type Reset Description 15 0 SYSRSTIV R 02h 03Eh 1 Reset interrupt vector Generates a value that can be used as address offset for fast interrupt service routine handling to identify the last cause...

Страница 83: ...ltage Supervisor SVS Chapter 2 SLAU367P October 2012 Revised April 2020 Power Management Module PMM and Supply Voltage Supervisor SVS This chapter describes the operation of the Power Management Module PMM and Supply Voltage Supervisor SVS The PMM is family specific Topic Page 2 1 Power Management Module PMM Introduction 84 2 2 PMM Operation 85 2 3 PMM Registers 88 ...

Страница 84: ... functions related to the power supply and its supervision for the device Its primary functions are first to generate a supply voltage for the core logic and second provide several mechanisms for the supervision of the voltage applied to the device DVCC The PMM uses an integrated low dropout voltage regulator LDO to produce a secondary core voltage VCORE from the primary one applied to the device ...

Страница 85: ...r modes Selected and active clocks Clock frequencies according to Clock System CS settings JTAG is active In addition to the main LDO an ultra low power regulator RTC LDO provides a regulated voltage to the real time clock module including the 32 kHz crystal oscillator and other ultra low power modules that remain active during LPM3 5 when the main LDO is off 2 2 2 Supply Voltage Supervisor The hi...

Страница 86: ...le LPMx 5 the PMMREGOFF bit in the PMMCTL0 register must be set The LOCKLPM5 bit in the PM5CTL0 register locks the I O configuration and other LPMx 5 relevant configurations after a wakeup from LPMx 5 until all the registers are configured again LPM3 5 and LPM4 5 can be configured with active SVS SVSHE 1 or with SVS disabled SVSHE 0 Disabling the SVS results in lower power consumption whereas enab...

Страница 87: ...sed as reset source for the rest of the application 2 2 7 PMM Interrupts Interrupt flags generated by the PMM are routed to the system NMI interrupt vector generator register SYSSNIV When the PMM causes a reset a value is generated in the system reset interrupt vector generator register SYSRSTIV corresponding to the source of the reset These registers are defined within the SYS module More informa...

Страница 88: ...s a PUC A write access to a register other than PMMCTL0 while write access is not enabled causes a PUC NOTE All registers have word or byte register access For a generic register ANYREG the suffix _L ANYREG_L refers to the lower byte of the register bits 0 through 7 The suffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 1 PMMCTL1 can be written as word only Table 2 1 PMM...

Страница 89: ...ritten with 0A5h to unlock the PMM registers 7 Reserved RW 0h Reserved Must be written with 0 6 SVSHE RW 1h High side SVS enable 0b High side SVS SVSH is disabled in LPM2 LPM3 LPM4 LPM3 5 and LPM4 5 SVSH is always enabled in active mode LPM0 and LPM1 1b SVSH is always enabled 5 Reserved R 0h Reserved Always reads as 0 4 PMMREGOFF RW 0h Regulator off 0b Regulator remains on when going into LPM3 or ...

Страница 90: ...age Supervisor SVS 2 3 2 PMMCTL1 Register offset 02h reset 9600h Power Management Module Control Register 1 Figure 2 5 PMMCTL1 Register 15 14 13 12 11 10 9 8 Reserved rw 1 rw 0 rw 0 rw 1 rw 0 rw 1 rw 1 rw 0 7 6 5 4 3 2 1 0 Reserved rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 r0 Table 2 3 PMMCTL1 Register Description Bit Field Type Reset Description 15 0 Reserved R 9600h Reserved Always reads as 9600h ...

Страница 91: ...set conditions The SVSHIFG interrupt flag is only set if the SVSH is the reset source that is if DVCC dropped below the high side SVS levels but remained above the brownout levels The bit is cleared by software or by reading the reset vector word SYSRSTIV 0b Reset not due to SVSH 1b Reset due to SVSH 12 11 Reserved R 0h Reserved Always reads as 0 10 PMMPORIFG RW 0h PMM software POR interrupt flag ...

Страница 92: ...cription 15 1 Reserved R 0h Reserved Always reads as 0 0 LOCKLPM5 RW 1h Locks I O pin and other LPMx 5 relevant for example RTC configurations upon exit from LPMx 5 This bit is set by hardware and must be cleared by software It cannot be set by software After a power cycle I O pins are locked in high impedance state with input Schmitt triggers disabled until LOCKLPM5 is cleared by the user softwar...

Страница 93: ...ents Incorporated Clock System CS Module Chapter 3 SLAU367P October 2012 Revised April 2020 Clock System CS Module This chapter describes the operation of the clock system which is implemented in all devices Topic Page 3 1 Clock System Introduction 94 3 2 Clock System Operation 96 3 3 MemoryMap Registers 103 ...

Страница 94: ...nternal low power oscillator with 5 MHz typical frequency LFMODCLK is MODCLK divided by 128 HFXTCLK High frequency oscillator that can be used with standard crystals or resonators in the 4 MHz to 24 MHz range When in bypass mode HFXTCLK can be driven with an external square wave signal Four system clock signals are available from the clock module ACLK Auxiliary clock The ACLK is software selectabl...

Страница 95: ...K VLO HFXTCLK VLOCLK 1 0 2 7 3 3 4 5 3 6 7 8 MHz 16 20 24 MHz DCOFSEL 3 Not available on all devices Fault Detection LFXIN LFXOUT LFXTBYPASS 1 0 1 LFXTDRIVE 2 HFXT HFXIN HFXOUT HFXTBYPASS 1 0 1 HFXTDRIVE 2 LFXT LFXTCLK rsvd rsvd rsvd rsvd rsvd rsvd rsvd rsvd rsvd LFXTCLK Fault Detection MODOSC MODOSC_REQEN MODOSC_REQ Unconditonal MODOSC requests EN MODOSC Enable Logic OSCOFF SELA 3 128 1 LFMODCLK ...

Страница 96: ...bility over operating temperature and supply voltage Low cost applications with less constrained clock accuracy requirements The CS module addresses these conflicting requirements by allowing the user to select from the three available clock signals ACLK MCLK and SMCLK A flexible clock distribution and divider system is provided to fine tune the individual clock requirements 3 2 2 LFXT Oscillator ...

Страница 97: ...isted in Table 3 1 In addition these bits should be configured properly before use of HFXT in either crystal or bypass modes of operation The HFXT pins are shared with general purpose I O ports At power up the default operation is HFXT crystal operation However HFXT remains disabled until the ports shared with HFXT are configured for HFXT operation The configuration of the shared I O is determined...

Страница 98: ... set MODOSCREQEN for modules that utilize unconditional requests for example ADC or fail safe MODOSC is enabled under any of the following conditions LFMODCLK is a source for ACLK SELAx 2 and in active mode AM through LPM3 OSCOFF 0 LFMODCLK or MODCLK is a source for MCLK SELMx 2 4 and in active mode AM CPUOFF 0 LFMODCLK or MODCLK is a source for SMCLK SELSx 2 4 and in active mode AM through LPM1 S...

Страница 99: ...l module causes its respective clock off signal to be overridden but does not change the setting of the clock off control bit For example a peripheral module may require ACLK that is currently disabled by the OSCOFF bit OSCOFF 1 The module can request ACLK by generating an ACLK_REQ This causes the OSCOFF bit to have no effect thereby allowing ACLK to be available to the requesting peripheral modul...

Страница 100: ...bled Disabled Disabled Disabled 3 2 8 CS Module Fail Safe Operation The CS module incorporates an oscillator fault fail safe feature This feature detects an oscillator fault for LFXT and HFXT as shown in Figure 3 3 The available fault conditions are Low frequency oscillator fault LFXTOFFG for LFXT High frequency oscillator fault HFXTOFFG for HFXT External clock signal faults for all bypass modes t...

Страница 101: ... The fault condition causes HFXTOFFG to be set and remain set If the user clears HFXTOFFG and the fault condition still exists HFXTOFFG remains set NOTE Fault logic As long as a fault condition still exists the OFIFG remains set The application must take special care when clearing the OFIFG signal If no fault condition remains when the OFIFG signal is cleared the clock logic switches back to the o...

Страница 102: ...dule 3 2 9 Synchronization of Clock Signals When switching ACLK MCLK or SMCLK from one clock source to the another the switch is synchronized to avoid critical race conditions see Figure 3 4 The current clock cycle continues until the next rising edge The clock remains high until the next rising edge of the new clock The new clock source is selected and continues with a full high period Figure 3 4...

Страница 103: ...in Table 3 3 should be considered as reserved locations and the register contents should not be modified Table 3 3 MEMORYMAP Registers Offset Acronym Register Name Section 0h CTL0 Clock System Control 0 Section 3 3 1 2h CTL1 Clock System Control 1 Section 3 3 2 4h CTL2 Clock System Control 2 Section 3 3 3 6h CTL3 Clock System Control 3 Section 3 3 4 8h CTL4 Clock System Control 4 Section 3 3 5 Ah ...

Страница 104: ...o the Summary Table Clock System Control 0 Register Figure 3 5 CTL0 Register 15 14 13 12 11 10 9 8 KEY R W 96h 7 6 5 4 3 2 1 0 RESERVED R 0h Table 3 4 CTL0 Register Field Descriptions Bit Field Type Reset Description 15 8 KEY R W 96h CSKEY password Must always be written with A5h a PUC is generated if any other value is written Always reads as 96h After the correct password is written all CS regis...

Страница 105: ...s this bit can be written by the user For low speed devices it is always reset See description of DCOFSEL bit for details 5 4 RESERVED R 0h Reserved Always reads as 0 3 1 DCOFSEL R W 6h DCO frequency select Selects frequency settings for the DCO Values shown below are approximate Please refer to the device specific datasheet 0h R W If DCORSEL 0 1 MHz If DCORSEL 1 1 MHz 1h R W If DCORSEL 0 2 67 MHz...

Страница 106: ...VED R 0h Reserved Always reads as 0 10 8 SELA R W 0h Selects the ACLK source 0h R W LFXTCLK LFXTCLK when LFXT available otherwise VLOCLK 1h R W VLOCLK VLOCLK 2h R W LFMODCLK LFMODCLK 7 RESERVED R 0h Reserved Always reads as 0 6 4 SELS R W 3h Selects the SMCLK source 0h R W LFXTCLK LFXTCLK when LFXT available otherwise VLOCLK 1h R W VLOCLK VLOCLK 2h R W LFMODCLK LFMODCLK 3h R W DCOCLK DCOCLK 4h R W...

Страница 107: ... 3h Table 3 7 CTL3 Register Field Descriptions Bit Field Type Reset Description 15 11 RESERVED R 0h Reserved Always reads as 0 10 8 DIVA R W 0h ACLK source divider Divides the frequency of the ACLK clock source 0h R W 1 1 1h R W 2 2 2h R W 4 4 3h R W 8 8 4h R W 16 16 5h R W 32 32 7 RESERVED R 0h Reserved Always reads as 0 6 4 DIVS R W 3h SMCLK source divider Divides the frequency of the SMCLK cloc...

Страница 108: ... bypass select 0h R W HFXT sourced from external crystal 1h R W HFXT sourced from external clock signal 11 10 HFFREQ R W 3h The HFXT frequency selection These bits must be set to the appropriate frequency for crystal or bypass modes of operation 0h R W 0 to 4 MHz 1h R W Greater than 4 MHz to 8 MHz 2h R W Greater than 8 MHz to 16 MHz 3h R W Greater than 16 MHz to 24 MHz 9 RESERVED R 0h Reserved Alw...

Страница 109: ...riptions continued Bit Field Type Reset Description 2 RESERVED R 0h Reserved Always reads as 0 1 SMCLKOFF R W 0h SMCLK off This bit turns off the SMCLK 0h R W SMCLK on 1h R W SMCLK off 0 LFXTOFF R W 1h LFXT off This bit turns off the LFXT 0h R W LFXT is on if LFXT is selected via the port selection and LFXT is not in bypass mode of operation 1h R W LFXT is off if it is not used as a source for ACL...

Страница 110: ...VED R 0h Reserved Always reads as 0 2 SWDONE R 1h Clock switch done This bit indicates a clock switch is done A clock switch happens when changing the clock system configuration including any write access of CSCTL1 CSCTL2 CSCTL3 registers or any fail safe condition happens When clock switch happens this bit is reset automatically and is set again after the switching is done Only available in CS_A ...

Страница 111: ... R W 0h MODCLK clock request enable Setting this enables conditional module requests for MODCLK 0h R W DISABLE MODCLK conditional requests are disabled 1h R W ENABLE MODCLK conditional requests are enabled 2 SMCLKREQEN R W 1h SMCLK clock request enable Setting this enables conditional module requests for SMCLK 0h R W DISABLE SMCLK conditional requests are disabled 1h R W ENABLE SMCLK conditional r...

Страница 112: ...UX with 1MB memory access its addressing modes and instruction set NOTE The MSP430X CPUX implemented on this device family formally called CPUXV2 has in some cases slightly different cycle counts from the MSP430X CPUX implemented on the F2xx and F4xx families Topic Page 4 1 MSP430X CPU CPUX Introduction 113 4 2 Interrupts 115 4 3 CPU Registers 116 4 4 Addressing Modes 122 4 5 MSP430 and MSP430X In...

Страница 113: ...atible with the MSP430 CPU The MSP430X CPU features include RISC architecture Orthogonal architecture Full register access including program counter PC status register SR and stack pointer SP Single cycle register operations Large register file reduces fetches to memory 20 bit address bus allows direct access and branching throughout the entire memory range without paging 16 bit data bus allows di...

Страница 114: ...General Purpose General Purpose General Purpose General Purpose General Purpose Memory Address Bus MAB MDB Memory Data Bus 16 20 16 20 bit ALU src dst Zero Z Carry C Overflow V Negative N MCLK 0 16 15 R2 SR Status Register MSP430X CPU CPUX Introduction www ti com 114 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figur...

Страница 115: ...ain 16 bit addresses that point into the lower 64KB memory This means all interrupt handlers must start in the lower 64KB memory During an interrupt the program counter PC and the status register SR are pushed onto the stack as shown in Figure 4 2 The MSP430X architecture stores the complete 20 bit PC value efficiently by appending the PC bits 19 16 to the stored SR value automatically on the stac...

Страница 116: ...ory The BR and CALL instructions reset the upper 4 PC bits to 0 Only addresses in the lower 64KB address range can be reached with the BR or CALL instruction When branching or calling addresses beyond the lower 64KB range can only be reached using the BRA or CALLA instructions Also any instruction to directly modify the PC does so according to the used addressing mode For example MOV W value PC cl...

Страница 117: ...l 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figure 4 6 shows the stack usage Figure 4 7 shows the stack usage when 20 bit address words are pushed Figure 4 5 Stack Pointer Figure 4 6 Stack Usage Figure 4 7 PUSHX A Format on the Stack Figure 4 8 shows the special cases of using the SP as an argument to the PUSH and POP instructions Figure 4 8 PUSH SP...

Страница 118: ...disable SCG0 System clock generator 0 This bit may be used to enable or disable functions in the clock system depending on the device family for example FLL enable or disable OSCOFF Oscillator off When this bit is set it turns off the LFXT1 crystal oscillator when LFXT1CLK is not used for MCLK or SMCLK In FRAM devices CPUOFF must be 1 to disable the cyrstal oscillator CPUOFF CPU off When this bit ...

Страница 119: ... bit processing R3 11 FFh FFFFh FFFFFh 1 word processing The constant generator advantages are No special instructions required No additional code word for the 6 constants No code memory access required to retrieve the constant The assembler uses the constant generator automatically if 1 of the 6 constants is used as an immediate source operand Registers R2 and R3 used in the constant mode cannot ...

Страница 120: ...8 Any word write to a register clears bits 19 16 The only exception is the SXT instruction The SXT instruction extends the sign through the complete 20 bit register Figure 4 10 through Figure 4 14 show the handling of byte word and address word data Note the reset of the leading most significant bits MSBs if a register is the destination of a byte or word instruction Figure 4 10 shows byte handlin...

Страница 121: ...CPU Registers 121 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figure 4 12 Word Register Operation Figure 4 13 and Figure 4 14 show 20 bit address word handling A suffix The handling is shown for a source register and a destination memory address word and for a source memory address word and a destination register Fi...

Страница 122: ...tored in combination of the preceding extension word and the next word Indexed mode X PC is used 01 1 Absolute ADDR The word following the instruction contains the absolute address X is stored in the next word or stored in combination of the preceding extension word and the next word Indexed mode X SR is used 10 Indirect register Rn Rn is used as a pointer to the operand 11 Indirect autoincrement ...

Страница 123: ...f the destination register Rdst The bits Rdst 19 8 are cleared The register Rsrc is not modified Word operation Word operation reads the 16 LSBs of the source register Rsrc and writes the result to the 16 LSBs of the destination register Rdst The bits Rdst 19 16 are cleared The register Rsrc is not modified Address word operation Address word operation reads the 20 bits of the source register Rsrc...

Страница 124: ...lated memory address is always located in the lower 64KB and does not overflow or underflow out of the lower 64KB memory space The RAM and the peripheral registers can be accessed this way and existing MSP430 software is usable without modifications as shown in Figure 4 15 Figure 4 15 Indexed Mode in Lower 64KB Length 2 or 3 words Operation The signed 16 bit index is located in the next word after...

Страница 125: ...um 0479Ch 1000h 0579Ch xxxxh xx32h 0579Eh 0579Ch xxxxh xx32h 0579Eh 0579Ch www ti com Addressing Modes 125 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 4 2 2 MSP430 Instruction With Indexed Mode in Upper Memory If the CPU register Rn points to an address above the lower 64KB memory the Rn bits 19 16 are used for th...

Страница 126: ...hich points to an address in the range 0 to FFFFFh The operand is the content of the addressed memory location Comment Valid for source and destination The assembler calculates the register index and inserts it Example ADD W 8346h R5 2100h R6 This instruction adds the 16 bit data contained in the source and the destination addresses and places the 16 bit result into the destination Source and dest...

Страница 127: ...1036h 23456h 15678h R5 R6 5596h 11034h xxxxh 2345h 1777Ah 17778h xxxxh 7777h 1777Ah 17778h 05432h 02345h 07777h src dst Sum 23456h F8346h 1B79Ch xxxxh 5432h 1B79Eh 1B79Ch xxxxh 5432h 1B79Eh 1B79Ch www ti com Addressing Modes 127 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figure 4 18 Example for Indexed Mode ...

Страница 128: ... bits Length 3 or 4 words Operation The operand address is the sum of the 20 bit CPU register content and the 20 bit index The 4 MSBs of the index are contained in the extension word the 16 LSBs are contained in the word following the instruction The CPU register is not modified Comment Valid for source and destination The assembler calculates the register index and inserts it Example ADDX A 12346...

Страница 129: ...ded 16 bit index in the next word after the instruction is added to the 20 bits of the CPU register Rn This delivers a 20 bit address which points to an address in the range 0 to FFFFFh The operand is the content of the addressed memory location Comment Valid for source and destination The assembler calculates the register index and inserts it Example MOVA 8002h R5 R6 R5 0x100 This instruction loa...

Страница 130: ...The RAM and the peripheral registers can be accessed this way and existing MSP430 software is usable without modifications as shown in Figure 4 19 Figure 4 19 Symbolic Mode Running in Lower 64KB Operation The signed 16 bit index in the next word after the instruction is added temporarily to the PC The resulting bits 19 16 are cleared giving a truncated 16 bit memory address which points to an oper...

Страница 131: ... xx32h 0579Eh 0579Ch xxxxh xx32h 0579Eh 0579Ch www ti com Addressing Modes 131 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 4 3 2 MSP430 Instruction With Symbolic Mode in Upper Memory If the PC points to an address above the lower 64KB memory the PC bits 19 16 are used for the address calculation of the operand The...

Страница 132: ...ess in the range 0 to FFFFFh The operand is the content of the addressed memory location Comment Valid for source and destination The assembler calculates the PC index and inserts it Example ADD W EDE TONI This instruction adds the 16 bit data contained in source word EDE and destination word TONI and places the 16 bit result into the destination word TONI For this example the instruction is locat...

Страница 133: ...66h PC 2F03Ah 2F038h 2F036h 5092h 2F034h xxxxh 5432h 3379Eh 3379Ch xxxxh 5432h 3379Eh 3379Ch 5432h 2345h 7777h src dst Sum xxxxh 2345h 0077Ah 00778h xxxxh 7777h 0077Ah 00778h www ti com Addressing Modes 133 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX ...

Страница 134: ...ge of PC 19 bits Length 3 or 4 words Operation The operand address is the sum of the 20 bit PC and the 20 bit index The 4 MSBs of the index are contained in the extension word the 16 LSBs are contained in the word following the instruction Comment Valid for source and destination The assembler calculates the register index and inserts it Example ADDX B EDE TONI This instruction adds the 8 bit data...

Страница 135: ...uction with absolute mode 4 4 4 1 Absolute Mode in Lower 64KB If an MSP430 instruction is used with absolute addressing mode the absolute address is a 16 bit value and therefore points to an address in the lower 64KB of the memory range The address is calculated as an index from 0 and is stored in the word following the instruction The RAM and the peripheral registers can be accessed this way and ...

Страница 136: ...used with absolute addressing mode the absolute address is a 20 bit value and therefore points to any address in the memory range The address value is calculated as an index from 0 The 4 MSBs of the index are contained in the extension word and the 16 LSBs are contained in the word following the instruction Length 3 or 4 words Operation The operand is the content of the addressed memory location C...

Страница 137: ...ect Register Mode The indirect register mode uses the contents of the CPU register Rsrc as the source operand The indirect register mode always uses a 20 bit address Length 1 2 or 3 words Operation The operand is the content the addressed memory location The source register Rsrc is not modified Comment Valid only for the source operand The substitute for the destination operand is 0 Rdst Example A...

Страница 138: ...e operand Rsrc is then automatically incremented by 1 for byte instructions by 2 for word instructions and by 4 for address word instructions immediately after accessing the source operand If the same register is used for source and destination it contains the incremented address for the destination access Indirect autoincrement mode always uses 20 bit addresses Length 1 2 or 3 words Operation The...

Страница 139: ...of the immediate operand the PC is incremented by 2 for byte word or address word instructions The immediate mode has 2 addressing possibilities 8 bit or 16 bit constants with MSP430 instructions 20 bit constants with MSP430X instruction 4 4 7 1 MSP430 Instructions With Immediate Mode If an MSP430 instruction is used with immediate addressing mode the constant is an 8 or 16 bit value and is stored...

Страница 140: ...nstruction is used with immediate addressing mode the constant is a 20 bit value The 4 MSBs of the constant are stored in the extension word and the 16 LSBs of the constant are stored in the word following the instruction Length 3 or 4 words 1 word less if a constant of the constant generator can be used for the immediate operand Operation The 20 bit immediate source operand is used together with ...

Страница 141: ...utine constants immediately after the subroutine code This allows the use of the symbolic addressing mode with its 16 bit index to reach addresses within the range of PC 32KB To use only MSP430X instructions The disadvantages of this method are the reduced speed due to the additional CPU cycles and the increased program space due to the necessary extension word for any double operand instruction U...

Страница 142: ...nd dst dst BIS B src dst src or dst dst XOR B src dst src xor dst dst Z AND B src dst src and dst dst 0 Z 4 5 1 2 MSP430 Single Operand Format II Instructions Figure 4 23 shows the format for MSP430 single operand instructions except RETI The destination word is appended for the indexed symbolic absolute and immediate modes Table 4 5 lists the 7 single operand instructions Figure 4 23 MSP430 Singl...

Страница 143: ...e bit is set JGE Label Jump to label if N XOR V 0 JL Label Jump to label if N XOR V 1 JMP Label Jump to label unconditionally 4 5 1 4 Emulated Instructions In addition to the MSP430 and MSP430X instructions emulated instructions are instructions that make code easier to write and read but do not have op codes themselves Instead they are replaced automatically by the assembler with a core instructi...

Страница 144: ...on the instruction format and the addressing modes used not the instruction itself The number of clock cycles refers to MCLK 4 5 1 5 1 Instruction Cycles and Length for Interrupt Reset and Subroutines Table 4 8 lists the length and the CPU cycles for reset interrupts and subroutines Table 4 8 Interrupt Return and Reset Cycles and Length Action Execution Time MCLK Cycles Length of Instruction Words...

Страница 145: ... and Length Addressing Mode No of Cycles Length of Instruction Example Source Destination Rn Rm 1 1 MOV R5 R8 PC 3 1 BR R9 x Rm 4 1 2 ADD R5 4 R6 EDE 4 1 2 XOR R8 EDE EDE 4 1 2 MOV R5 EDE Rn Rm 2 1 AND R4 R5 PC 4 1 BR R8 x Rm 5 1 2 XOR R5 8 R6 EDE 5 1 2 MOV R5 EDE EDE 5 1 2 XOR R5 EDE Rn Rm 2 1 ADD R5 R6 PC 4 1 BR R9 x Rm 5 1 2 XOR R5 8 R6 EDE 5 1 2 MOV R9 EDE EDE 5 1 2 MOV R9 EDE N Rm 2 2 MOV 20 ...

Страница 146: ... Figure 4 25 Extension Word for Register Modes Table 4 11 Description of the Extension Word Bits for Register Mode Bit Description 15 11 Extension word op code Op codes 1800h to 1FFFh are extension words 10 9 Reserved ZC Zero carry 0 The executed instruction uses the status of the carry bit C 1 The executed instruction uses the carry bit as 0 The carry bit is defined by the result of the final ope...

Страница 147: ...s 1800h to 1FFFh are extension words Source Bits 19 16 The 4 MSBs of the 20 bit source Depending on the source addressing mode these 4 MSBs may belong to an immediate operand an index or to an absolute address A L Data length extension Together with the B W bits of the following MSP430 instruction the AL bit defines the used data length of the instruction A L B W Comment 0 0 Reserved 0 1 20 bit ad...

Страница 148: ...ndexed Instruction 4 5 2 3 Extended Double Operand Format I Instructions All 12 double operand instructions have extended versions as listed in Table 4 13 1 Status bit is affected Status bit is not affected 0 Status bit is cleared 1 Status bit is set Table 4 13 Extended Double Operand Instructions Mnemonic Operands Operation Status Bits 1 V N Z C MOVX B A src dst src dst ADDX B A src dst src dst d...

Страница 149: ... 19 16 0 0 0 0 As src 19 16 As dst 15 0 www ti com MSP430 and MSP430X Instructions 149 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figure 4 29 shows the possible addressing combinations for the extension word for Format I instructions Figure 4 29 Extended Format I Instruction Formats If the 20 bit address of a sourc...

Страница 150: ...egisters from stack 1 to 16 POPM W n Rdst Pop n 16 bit registers from stack 1 to 16 PUSHM A n Rsrc Push n 20 bit registers to stack 1 to 16 PUSHM W n Rsrc Push n 16 bit registers to stack 1 to 16 PUSHX B A src Push 8 16 or 20 bit source to stack RRCM A n Rdst Rotate right Rdst n bits through carry 16 20 bit register 1 to 4 0 RRUM A n Rdst Rotate right Rdst n bits unsigned 16 20 bit register 1 to 4...

Страница 151: ...om MSP430 and MSP430X Instructions 151 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 5 2 4 1 Extended Format II Instruction Format Exceptions Exceptions for the Format II instruction formats are shown in Figure 4 32 through Figure 4 35 Figure 4 32 PUSHM and POPM Instruction Format Figure 4 33 RRCM RRAM RRUM and RLAM...

Страница 152: ... CLRA Rdst Clear Rdst MOV 0 Rdst CLRX B A dst Clear dst MOVX B A 0 dst DADCX B A dst Add carry to dst decimally DADDX B A 0 dst DECX B A dst Decrement dst by 1 SUBX B A 1 dst DECDA Rdst Decrement Rdst by 2 SUBA 2 Rdst DECDX B A dst Decrement dst by 2 SUBX B A 2 dst INCX B A dst Increment dst by 1 ADDX B A 1 dst INCDA Rdst Increment Rdst by 2 ADDA 2 Rdst INCDX B A dst Increment dst by 2 ADDX B A 2 ...

Страница 153: ... extension word op code improving code density and execution time Address instructions should be used any time an MSP430X instruction is needed with the corresponding restricted addressing mode 1 Status bit is affected Status bit is not affected 0 Status bit is cleared 1 Status bit is set Table 4 16 Address Instructions Operate on 20 Bit Register Data Mnemonic Operands Operation Status Bits 1 V N ...

Страница 154: ...nd Lengths Table 4 17 lists the length and the CPU cycles for all addressing modes of the MSP430X extended single operand instructions 1 Add 1 cycle when Rn SP Table 4 17 MSP430X Format II Instruction Cycles and Length Instruction Execution Cycles Length of Instruction Words Rn Rn Rn N X Rn EDE EDE RRAM n 1 RRCM n 1 RRUM n 1 RLAM n 1 PUSHM 2 n 1 PUSHM A 2 2n 1 POPM 2 n 1 POPM A 2 2n 1 CALLA 5 1 6 ...

Страница 155: ... Destination B W A B W A Rn Rm 1 2 2 2 BITX B R5 R8 PC 4 4 2 ADDX R9 PC x Rm 5 2 7 3 3 ANDX A R5 4 R6 EDE 5 2 7 3 3 XORX R8 EDE EDE 5 2 7 3 3 BITX W R5 EDE Rn Rm 3 4 2 BITX R5 R8 PC 5 6 2 ADDX R9 PC x Rm 6 2 9 3 3 ANDX A R5 4 R6 EDE 6 2 9 3 3 XORX R8 EDE EDE 6 2 9 3 3 BITX B R5 EDE Rn Rm 3 4 2 BITX R5 R8 PC 5 6 2 ADDX A R9 PC x Rm 6 2 9 3 3 ANDX R5 4 R6 EDE 6 2 9 3 3 XORX B R8 EDE EDE 6 2 9 3 3 BI...

Страница 156: ...19 Address Instruction Cycles and Length Addressing Mode Execution Time MCLK Cycles Length of Instruction Words Example Source Destination MOVA BRA CMPA ADDA SUBA MOVA CMPA ADDA SUBA Rn Rn 1 1 1 1 CMPA R5 R8 PC 3 3 1 1 SUBA R9 PC x Rm 4 2 MOVA R5 4 R6 EDE 4 2 MOVA R8 EDE EDE 4 2 MOVA R5 EDE Rn Rm 3 1 MOVA R5 R8 PC 5 1 MOVA R9 PC Rn Rm 3 1 MOVA R5 R8 PC 5 1 MOVA R9 PC N Rm 2 3 2 2 CMPA 20 R8 PC 3 3...

Страница 157: ...80 1C0 200 240 280 2C0 300 340 380 3C0 0xxx MOVA CMPA ADDA SUBA RRCM RRAM RLAM RRUM 10xx RRC RRC B SWP B RRA RRA B SXT PUS H PUS H B CALL RETI CALL A 14xx PUSHM A POPM A PUSHM W POPM W 18xx Extension word for Format I and Format II instructions 1Cxx 20xx JNE JNZ 24xx JEQ JZ 28xx JNC 2Cxx JC 30xx JN 34xx JGE 38xx JL 3Cxx JMP 4xxx MOV MOV B 5xxx ADD ADD B 6xxx ADDC ADDC B 7xxx SUBC SUBC B 8xxx SUB S...

Страница 158: ... 0 0 imm 19 16 1 0 0 0 dst MOVA imm20 Rdst imm 15 0 CMPA 0 0 0 0 imm 19 16 1 0 0 1 dst CMPA imm20 Rdst imm 15 0 ADDA 0 0 0 0 imm 19 16 1 0 1 0 dst ADDA imm20 Rdst imm 15 0 SUBA 0 0 0 0 imm 19 16 1 0 1 1 dst SUBA imm20 Rdst imm 15 0 MOVA 0 0 0 0 src 1 1 0 0 dst MOVA Rsrc Rdst CMPA 0 0 0 0 src 1 1 0 1 dst CMPA Rsrc Rdst ADDA 0 0 0 0 src 1 1 1 0 dst ADDA Rsrc Rdst SUBA 0 0 0 0 src 1 1 1 1 dst SUBA Rs...

Страница 159: ... 0 1 dst CALLA x Rdst x 15 0 0 0 0 1 0 0 1 1 0 1 1 0 dst CALLA Rdst 0 0 0 1 0 0 1 1 0 1 1 1 dst CALLA Rdst 0 0 0 1 0 0 1 1 1 0 0 0 abs 19 16 CALLA abs20 abs 15 0 0 0 0 1 0 0 1 1 1 0 0 1 x 19 16 CALLA EDE x 15 0 CALLA x PC 0 0 0 1 0 0 1 1 1 0 1 1 imm 19 16 CALLA imm20 imm 15 0 Reserved 0 0 0 1 0 0 1 1 1 0 1 0 x x x x Reserved 0 0 0 1 0 0 1 1 1 1 x x x x x x PUSHM A 0 0 0 1 0 1 0 0 n 1 dst PUSHM A n...

Страница 160: ...i com 160 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 6 2 MSP430 Instructions The MSP430 instructions are listed and described on the following pages ...

Страница 161: ...estination are lost Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Set if dst was incremented from 0FFFFh to 0000 reset otherwise Set if dst was incremented from 0FFh to 00 reset otherwise V Set if an arithmetic overflow occurs otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 16 bit counter pointed to by R13 is added ...

Страница 162: ... carry from the MSB of the result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is positive reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example 10 is added to the 16 bit counter CNTR located in lower 64 K ADD W 10 CNTR Add 10 to 16 bit counter Example A table word pointed to by R5 20 bit address in R5 is added to ...

Страница 163: ...f the result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is positive reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example Constant value 15 and the carry of the previous instruction are added to the 16 bit counter CNTR located in lower 64 K ADDC W 15 CNTR Add 15 C to 16 bit CNTR Example A table word pointed to by...

Страница 164: ...its N Set if result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if the result is not zero reset otherwise C not Z V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The bits set in R5 16 bit data are used as a mask AA55h for the word TOM located in the lower 64 K If the result is zero a branch is taken to label TONI R5 19 16 0 MOV AA55h R5 ...

Страница 165: ...rand and the destination operand are logically ANDed The result is placed into the destination The source operand is not affected Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The bits 15 14 of R5 16 bit data are cleared R5 19 16 0 BIC 0C000h R5 Clear R5 19 14 bits Example A table word pointed to by R5 20 bit addres...

Страница 166: ...he destination operand are logically ORed The result is placed into the destination The source operand is not affected Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Bits 15 and 13 of R5 16 bit data are set to 1 R5 19 16 0 BIS A000h R5 Set R5 bits Example A table word pointed to by R5 20 bit address is used to set bi...

Страница 167: ...esult is zero reset otherwise C Set if the result is not zero reset otherwise C not Z V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example Test if 1 or both of bits 15 and 14 of R5 16 bit data is set Jump to label TONI if this is the case R5 19 16 are not affected BIT C000h R5 Test R5 15 14 bits JNZ TONI At least 1 bit is set in R5 Both bits are reset Example A table word pointed to by...

Страница 168: ...the address contained in EXEC Core instruction MOV X PC PC Indirect address BR EXEC Branch to the address contained in absolute address EXEC Core instruction MOV X 0 PC Indirect address BR R5 Branch to the address contained in R5 Core instruction MOV R5 PC Indirect R5 BR R5 Branch to the address contained in the word pointed to by R5 Core instruction MOV R5 PC Indirect indirect R5 BR R5 Branch to ...

Страница 169: ...9 16 cleared address in lower 64 K Mode Bits OSCOFF CPUOFF and GIE are not affected Examples Examples for all addressing modes are given Immediate Mode Call a subroutine at label EXEC lower 64 K or call directly to address CALL EXEC Start address EXEC CALL 0AA04h Start address 0AA04h Symbolic Mode Call a subroutine at the 16 bit address contained in address EXEC EXEC is located at the address PC X...

Страница 170: ...4 6 2 10 CLR CLR W Clear destination CLR B Clear destination Syntax CLR dst or CLR W dst CLR B dst Operation 0 dst Emulation MOV 0 dst MOV B 0 dst Description The destination operand is cleared Status Bits Status bits are not affected Example RAM word TONI is cleared CLR TONI 0 TONI Example Register R5 is cleared CLR R5 Example RAM byte TONI is cleared CLR B TONI 0 TONI ...

Страница 171: ... SR Description The carry bit C is cleared The clear carry instruction is a word instruction Status Bits N Not affected Z Not affected C Cleared V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 16 bit decimal counter pointed to by R13 is added to a 32 bit counter pointed to by R12 CLRC C 0 defines start DADD R13 0 R12 add 16 bit counter to low word of 32 bit counter DADC...

Страница 172: ...t 04h is inverted 0FFFBh and is logically ANDed with the destination operand The result is placed into the destination The clear negative bit instruction is a word instruction Status Bits N Reset to 0 Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The negative bit in the SR is cleared This avoids special treatment with negative numbers of the ...

Страница 173: ...fected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The zero bit in the SR is cleared CLRZ Indirect Auto Increment mode Call a subroutine at the 16 bit address contained in the word pointed to by register R5 20 bit address and increment the 16 bit address in R5 afterwards by 2 The next time the software uses R5 as a pointer it can alter the program execution due to access to the next w...

Страница 174: ...ction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOFF CPUOFF and GIE are not affected Example Compare word EDE with a 16 bit constant 1800h Jump to label TONI if EDE equals the constant The address...

Страница 175: ...s 1 Z Set if dst is 0 reset otherwise C Set if destination increments from 9999 to 0000 reset otherwise Set if destination increments from 99 to 00 reset otherwise V Undefined Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 4 digit decimal number contained in R5 is added to an 8 digit decimal number pointed to by R8 CLRC Reset carry next instruction s start condition is defined DADD R...

Страница 176: ...s Bits N Set if MSB of result is 1 word 7999h byte 79h reset if MSB is 0 Z Set if result is zero reset otherwise C Set if the BCD result is too large word 9999h byte 99h reset otherwise V Undefined Mode Bits OSCOFF CPUOFF and GIE are not affected Example Decimal 10 is added to the 16 bit BCD counter DECCNTR DADD 10h DECCNTR Add 10 to 4 digit BCD counter Example The 8 digit BCD number contained in ...

Страница 177: ...reset otherwise C Reset if dst contained 0 set otherwise V Set if an arithmetic overflow occurs otherwise reset Set if initial value of destination was 08000h otherwise reset Set if initial value of destination was 080h otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example R10 is decremented by 1 DEC R10 Decrement R10 Move a block of 255 bytes from memory location starting with ...

Страница 178: ...if dst contained 0 or 1 set otherwise V Set if an arithmetic overflow occurs otherwise reset Set if initial value of destination was 08001 or 08000h otherwise reset Set if initial value of destination was 081 or 080h otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example R10 is decremented by 2 DECD R10 Decrement R10 by 2 Move a block of 255 bytes from memory location starting wi...

Страница 179: ...s ensures that the counter is not modified during the move by any interrupt DINT All interrupt events using the GIE bit are disabled NOP Required due to pipelined CPU architecture MOV COUNTHI R5 Copy counter MOV COUNTLO R6 EINT All interrupt events using the GIE bit are enabled NOTE Disable interrupt Due to the pipelined CPU architecture clearing the general interrupt enable GIE requires special c...

Страница 180: ...are allowed BIT Mask SP JEQ MaskOK Flags are present identically to mask jump MaskOK BIC Mask SP INCD SP Housekeeping inverse to PUSH instruction at the start of interrupt subroutine Corrects the stack pointer RETI NOTE Enable interrupt Due to the pipelined CPU architecture setting the general interrupt enable GIE requires special care The instruction immediately after the enable interrupts instru...

Страница 181: ...remented by 1 The original contents are lost Status Bits N Set if result is negative reset if positive Z Set if dst contained 0FFFFh reset otherwise Set if dst contained 0FFh reset otherwise C Set if dst contained 0FFFFh reset otherwise Set if dst contained 0FFh reset otherwise V Set if dst contained 07FFFh reset otherwise Set if dst contained 07Fh reset otherwise Mode Bits OSCOFF CPUOFF and GIE a...

Страница 182: ...ontained 0FFFEh reset otherwise Set if dst contained 0FEh reset otherwise C Set if dst contained 0FFFEh or 0FFFFh reset otherwise Set if dst contained 0FEh or 0FFh reset otherwise V Set if dst contained 07FFEh or 07FFFh reset otherwise Set if dst contained 07Eh or 07Fh reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example The item on the top of the stack TOS is removed without u...

Страница 183: ...re lost Status Bits N Set if result is negative reset if positive Z Set if dst contained 0FFFFh reset otherwise Set if dst contained 0FFh reset otherwise C Set if result is not zero reset otherwise NOT Zero V Set if initial destination operand was negative otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example Content of R5 is negated twos complement MOV 00AEh R5 R5 000AEh INV R5...

Страница 184: ...e 511 to 512 words relative to the PC in the full memory range If C is reset the instruction after the jump is executed JC is used for the test of the carry bit C JHS is used for the comparison of unsigned numbers Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The state of the port 1 pin P1IN 1 bit defines the program flow BIT B 2 P1IN Port 1 bit ...

Страница 185: ... the PC in the full memory range If Z is reset the instruction after the jump is executed JZ is used for the test of the zero bit Z JEQ is used for the comparison of operands Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The state of the P2IN 0 bit defines the program flow BIT B 1 P2IN Port 2 bit 0 reset JZ Label1 Yes proceed at Label1 No set con...

Страница 186: ...rands also for incorrect results due to overflow the decision made by the JGE instruction is correct Note that JGE emulates the nonimplemented JP jump if positive instruction if used after the instructions AND BIT RRA SXTX and TST These instructions clear the V bit Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example If byte EDE lower 64 K contains posi...

Страница 187: ...struction after the jump is executed JL is used for the comparison of signed operands also for incorrect results due to overflow the decision made by the JL instruction is correct Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example If byte EDE contains a smaller signed operand than byte TONI continue at Label1 The address EDE is within PC 32 K CMP B TO...

Страница 188: ...used as a BR or BRA instruction within its limited range relative to the PC Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The byte STATUS is set to 10 Then a jump to label MAINLOOP is made Data in lower 64 K program in full memory range MOV B 10 STATUS Set STATUS to 10 JMP MAINLOOP Go to main loop Example The interrupt vector TAIV of Timer_A3 is ...

Страница 189: ...emory range If N is reset the instruction after the jump is executed Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The byte COUNT is tested If it is negative program execution continues at Label0 Data in lower 64 K program in full memory range TST B COUNT Is byte COUNT negative JN Label0 Yes proceed at Label0 COUNT 0 Example R6 is subtracted from...

Страница 190: ... This means a jump in the range 511 to 512 words relative to the PC in the full memory range If C is set the instruction after the jump is executed JNC is used for the test of the carry bit C JLO is used for the comparison of unsigned numbers Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example If byte EDE 15 the program continues at Label2 Unsigned dat...

Страница 191: ...ruction after the jump is executed JNZ is used for the test of the zero bit Z JNE is used for the comparison of operands Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The byte STATUS is tested If it is not zero the program continues at Label3 The address of STATUS is within PC 32 K TST B STATUS Is STATUS 0 JNZ Label3 No proceed at Label3 Yes cont...

Страница 192: ...0h to absolute address word EDE lower 64 K MOV 01800h EDE Move 1800h to EDE Example The contents of table EDE word data 16 bit addresses are copied to table TOM The length of the tables is 030h words Both tables reside in the lower 64 K MOV EDE R10 Prepare pointer 16 bit address Loop MOV R10 TOM EDE 2 R10 R10 points to both tables R10 2 CMP EDE 60h R10 End of table reached JLO Loop Not yet Copy co...

Страница 193: ...ght 2012 2020 Texas Instruments Incorporated CPUX 4 6 2 33 NOP NOP No operation Syntax NOP Operation None Emulation MOV 0 R3 Description No operation is performed The instruction may be used for the elimination of instructions during the software check or for defined waiting times Status Bits Status bits are not affected ...

Страница 194: ...ts of R7 and the SR are restored from the stack POP R7 Restore R7 POP SR Restore status register Example The contents of RAM byte LEO is restored from the stack POP B LEO The low byte of the stack is moved to LEO Example The contents of R7 is restored from the stack POP B R7 The low byte of the stack is moved to R7 the high byte of R7 is 00h Example The contents of the memory pointed to by R7 and ...

Страница 195: ...ption The 20 bit SP SP is decremented by 2 The operand is then copied to the RAM word addressed by the SP A pushed byte is stored in the low byte the high byte is not affected Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Save the 2 16 bit registers R9 and R10 on the stack PUSH R9 Save R9 and R10 XXXXh PUSH R10 YYYYh Example Save the 2 bytes EDE ...

Страница 196: ...ss lower 64 K pushed onto the stack by a CALL instruction is restored to the PC The program continues at the address following the subroutine call The 4 MSBs of the PC 19 16 are cleared Status Bits Status bits are not affected PC 19 16 Cleared Mode Bits OSCOFF CPUOFF and GIE are not affected Example Call a subroutine SUBR in the lower 64 K and return to the address in the lower 64 K after the CALL...

Страница 197: ...rom same stack location as the status bits and PC 15 0 The 20 bit PC is restored to the value at the beginning of the interrupt service routine The program continues at the address following the last executed instruction when the interrupt was granted The SP is incremented by 2 afterward No interrupt flags are modified by this command Status Bits N Restored from stack C Restored from stack Z Resto...

Страница 198: ...e result has changed sign Figure 4 38 Destination Operand Arithmetic Shift Left An overflow occurs if dst 040h and dst 0C0h before the operation is performed the result has changed sign Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Loaded from the MSB V Set if an arithmetic overflow occurs the initial value is 04000h dst 0C000h reset otherwise ...

Страница 199: ...Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Loaded from the MSB V Set if an arithmetic overflow occurs the initial value is 04000h dst 0C000h reset otherwise Set if an arithmetic overflow occurs the initial value is 040h dst 0C0h reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example R5 is shifted left 1 position RLC R5 R5 x...

Страница 200: ...lly by 1 bit position as shown in Figure 4 40 The MSB retains its value sign RRA operates equal to a signed division by 2 The MSB is retained and shifted into the MSB 1 The LSB 1 is shifted into the LSB The previous LSB is shifted into the carry bit C Status Bits N Set if result is negative MSB 1 reset otherwise MSB 0 Z Set if result is zero reset otherwise C Loaded from the LSB V Reset Mode Bits ...

Страница 201: ... dst Operation C MSB MSB 1 LSB 1 LSB C Description The destination operand is shifted right by 1 bit position as shown in Figure 4 41 The carry bit C is shifted into the MSB and the LSB is shifted into the carry bit C Status Bits N Set if result is negative MSB 1 reset otherwise MSB 0 Z Set if result is zero reset otherwise C Loaded from the LSB V Reset Mode Bits OSCOFF CPUOFF and GIE are not affe...

Страница 202: ...tus Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Set if there is a carry from the MSB of the result reset otherwise Set to 1 if no borrow reset if borrow V Set if an arithmetic overflow occurs reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 16 bit counter pointed to by R13 is subtracted from a 32 bit counter pointed to by...

Страница 203: ...y bit C is set Status Bits N Not affected Z Not affected C Set V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Emulation of the decimal subtraction Subtract R5 from R6 decimally Assume that R5 03987h and R6 04137h DSUB ADD 06666h R5 Move content R5 from 0 9 to 6 0Fh R5 03987h 06666h 09FEDh INV R5 Invert this result back to 0 9 R5 NOT R5 06012h SETC Prepare carry 1 DADD R5 R...

Страница 204: ...ation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 6 2 44 SETN SETN Set negative bit Syntax SETN Operation 1 N Emulation BIS 4 SR Description The negative bit N is set Status Bits N Set Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected ...

Страница 205: ...mentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 6 2 45 SETZ SETZ Set zero bit Syntax SETZ Operation 1 N Emulation BIS 2 SR Description The zero bit Z is set Status Bits N Not affected Z Set C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected ...

Страница 206: ...ise src dst C Set if there is a carry from the MSB reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOFF CPUOFF and GIE are not affected Example A 16 bit constant...

Страница 207: ...a carry from the MSB reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOFF CPUOFF and GIE are not affected Example A 16 bit constant 7654h is subtracted from R5 w...

Страница 208: ...pyright 2012 2020 Texas Instruments Incorporated CPUX 4 6 2 48 SWPB SWPB Swap bytes Syntax SWPB dst Operation dst 15 8 dst 7 0 Description The high and the low byte of the operand are exchanged PC 19 16 bits are cleared in register mode Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Exchange the bytes of RAM word EDE lower 64 K MOV 1234h EDE 1234h...

Страница 209: ...ended into the high byte dst 7 0 high byte 00h afterwards dst 7 1 high byte FFh afterwards Status Bits N Set if result is negative reset otherwise Z Set if result is zero reset otherwise C Set if result is not zero reset otherwise C not Z V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The signed 8 bit data in EDE lower 64 K is sign extended and added to the 16 bit signed data in ...

Страница 210: ...negative reset if positive Z Set if destination contains zero reset otherwise C Set V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example R7 is tested If it is negative continue at R7NEG if it is positive but not zero continue at R7POS TST R7 Test R7 JN R7NEG R7 is negative JZ R7ZERO R7 is zero R7POS R7 is positive but not zero R7NEG R7 is negative R7ZERO R7 is zero Example The low byte...

Страница 211: ... result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if result is not zero reset otherwise C not Z V Set if both operands are negative before execution reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example Toggle bits in word CNTR 16 bit data with information bit 1 in address word TONI Both operands are located in lower 64 K XOR TONI CN...

Страница 212: ...tended Instructions The extended MSP430X instructions give the MSP430X CPU full access to its 20 bit address space MSP430X instructions require an additional word of op code called the extension word All addresses indexes and immediate numbers have 20 bit values when preceded by the extension word The MSP430X extended instructions are listed and described in the following pages ...

Страница 213: ...CX B 0 dst Description The carry bit C is added to the destination operand The previous contents of the destination are lost Status Bits N Set if result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if there is a carry from the MSB of the result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is...

Страница 214: ...e is a carry from the MSB of the result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is positive reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example 10 is added to the 20 bit pointer CNTR located in 2 words CNTR LSBs and CNTR 2 MSBs ADDX A 10 CNTR Add 10 to 20 bit pointer Example A table word 16 bit pointed to by...

Страница 215: ...e MSB 0 Z Set if result is zero reset otherwise C Set if there is a carry from the MSB of the result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is positive reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example Constant 15 and the carry of the previous instruction are added to the 20 bit counter CNTR located in 2 ...

Страница 216: ...s not affected Both operands may be located in the full address space Status Bits N Set if result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if the result is not zero reset otherwise C not Z V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The bits set in R5 20 bit data are used as a mask AAA55h for the address word TOM located in 2 word...

Страница 217: ...tion The inverted source operand and the destination operand are logically ANDed The result is placed into the destination The source operand is not affected Both operands may be located in the full address space Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example The bits 19 15 of R5 20 bit data are cleared BICX A 0F8000...

Страница 218: ...st Description The source operand and the destination operand are logically ORed The result is placed into the destination The source operand is not affected Both operands may be located in the full address space Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Bits 16 and 15 of R5 20 bit data are set to 1 BISX A 01800...

Страница 219: ... Bits N Set if result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if the result is not zero reset otherwise C not Z V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example Test if bit 16 or 15 of R5 20 bit data is set Jump to label TONI if so BITX A 018000h R5 Test R5 16 15 bits JNZ TONI At least 1 bit is set Both are reset Example A table word ...

Страница 220: ... destination address word CLRX W Clear destination word CLRX B Clear destination byte Syntax CLRX A dst CLRX dst or CLRX W dst CLRX B dst Operation 0 dst Emulation MOVX A 0 dst MOVX 0 dst MOVX B 0 dst Description The destination operand is cleared Status Bits Status bits are not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example RAM address word TONI is cleared CLRX A TONI 0 TONI ...

Страница 221: ...B reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOFF CPUOFF and GIE are not affected Example Compare EDE with a 20 bit constant 18000h Jump to label TONI if ED...

Страница 222: ...peration dst C dst decimally Emulation DADDX A 0 dst DADDX 0 dst DADDX B 0 dst Description The carry bit C is added decimally to the destination Status Bits N Set if MSB of result is 1 address word 79999h word 7999h byte 79h reset if MSB is 0 Z Set if result is zero reset otherwise C Set if the BCD result is too large address word 99999h word 9999h byte 99h reset otherwise V Undefined Mode Bits OS...

Страница 223: ...sult is not defined for non BCD numbers Both operands may be located in the full address space Status Bits N Set if MSB of result is 1 address word 79999h word 7999h byte 79h reset if MSB is 0 Z Set if result is zero reset otherwise C Set if the BCD result is too large address word 99999h word 9999h byte 99h reset otherwise V Undefined Mode Bits OSCOFF CPUOFF and GIE are not affected Example Decim...

Страница 224: ...st DECX dst or DECX W dst DECX B dst Operation dst 1 dst Emulation SUBX A 1 dst SUBX 1 dst SUBX B 1 dst Description The destination operand is decremented by 1 The original contents are lost Status Bits N Set if result is negative reset if positive Z Set if dst contained 1 reset otherwise C Reset if dst contained 0 set otherwise V Set if an arithmetic overflow occurs otherwise reset Mode Bits OSCO...

Страница 225: ...ECDX A dst DECDX dst or DECDX W dst DECDX B dst Operation dst 2 dst Emulation SUBX A 2 dst SUBX 2 dst SUBX B 2 dst Description The destination operand is decremented by 2 The original contents are lost Status Bits N Set if result is negative reset if positive Z Set if dst contained 2 reset otherwise C Reset if dst contained 0 or 1 set otherwise V Set if an arithmetic overflow occurs otherwise rese...

Страница 226: ...incremented by 1 The original contents are lost Status Bits N Set if result is negative reset if positive Z A Set if dst contained 0FFFFFh reset otherwise W Set if dst contained 0FFFFh reset otherwise B Set if dst contained 0FFh reset otherwise C A Set if dst contained 0FFFFFh reset otherwise W Set if dst contained 0FFFFh reset otherwise B Set if dst contained 0FFh reset otherwise V A Set if dst c...

Страница 227: ...riginal contents are lost Status Bits N Set if result is negative reset if positive Z A Set if dst contained 0FFFFEh reset otherwise W Set if dst contained 0FFFEh reset otherwise B Set if dst contained 0FEh reset otherwise C A Set if dst contained 0FFFFEh or 0FFFFFh reset otherwise W Set if dst contained 0FFFEh or 0FFFFh reset otherwise B Set if dst contained 0FEh or 0FFh reset otherwise V A Set i...

Страница 228: ...inverted The original contents are lost Status Bits N Set if result is negative reset if positive Z A Set if dst contained 0FFFFFh reset otherwise W Set if dst contained 0FFFFh reset otherwise B Set if dst contained 0FFh reset otherwise C Set if result is not zero reset otherwise NOT Zero V Set if initial destination operand was negative otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affe...

Страница 229: ...OM The length of the table is 030h words MOVA EDE R10 Prepare pointer 20 bit address Loop MOVX W R10 TOM EDE 2 R10 R10 points to both tables R10 2 CMPA EDE 60h R10 End of table reached JLO Loop Not yet Copy completed Example The contents of table EDE byte data 20 bit addresses are copied to table TOM The length of the table is 020h bytes MOVA EDE R10 Prepare pointer 20 bit MOV 20h R9 Prepare count...

Страница 230: ...ubmit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX MOVX A z20 Rsrc Rdst MOVA z16 Rsrc Rdst Indexed Reg MOVX A Rsrc z20 Rdst MOVA Rsrc z16 Rdst Reg Indexed MOVX A symb20 Rdst MOVA symb16 Rdst Symbolic Reg MOVX A Rsrc symb20 MOVA Rsrc symb16 Reg Symbolic ...

Страница 231: ...restored from stack The 16 bit values from stack 1 word per register are restored to the CPU registers Note This instruction does not use the extension word Description POPM A The CPU registers pushed on the stack are moved to the extended CPU registers starting with the CPU register Rdst n 1 The SP is incremented by n 4 after the operation POPM W The 16 bit registers pushed on the stack are moved...

Страница 232: ... decremented by 2 for each register stored on the stack Description PUSHM A The n CPU registers starting with Rdst backwards are stored on the stack The SP is decremented by n 4 after the operation The data Rn 19 0 of the pushed CPU registers is not affected PUSHM W The n registers starting with Rdst backwards are stored on the stack The SP is decremented by n 2 after the operation The data Rn 19 ...

Страница 233: ...nation 20 bit addresses are possible The SP is incremented by 2 byte and word operands and by 4 address word operand Emulation MOVX B A SP dst Description The item on TOS is written to the destination operand Register mode indexed mode symbolic mode and absolute mode are possible The SP is incremented by 2 or 4 Note the SP is incremented by 2 also for byte operations Status Bits Status bits are no...

Страница 234: ...rand on the TOS 20 bit addresses are possible The SP is decremented by 2 byte and word operands or by 4 address word operand before the write operation Description The SP is decremented by 2 byte and word operands or by 4 address word operand Then the source operand is written to the TOS All 7 addressing modes are possible for the source operand Status Bits Status bits are not affected Mode Bits O...

Страница 235: ...ted arithmetically left 1 2 3 or 4 positions as shown in Figure 4 44 RLAM works as a multiplication signed and unsigned with 2 4 8 or 16 The word instruction RLAM W clears the bits Rdst 19 16 Note This instruction does not use the extension word Status Bits N Set if result is negative A Rdst 19 1 reset if Rdst 19 0 W Rdst 15 1 reset if Rdst 15 0 Z Set if result is zero reset otherwise C Loaded fro...

Страница 236: ...own in Figure 4 45 The MSB is shifted into the carry bit C and the LSB is filled with 0 The RLAX instruction acts as a signed multiplication by 2 Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Loaded from the MSB V A Set if an arithmetic overflow occurs the initial value is 040000h dst 0C0000h reset otherwise W Set if an arithmetic overflow occu...

Страница 237: ... is shifted into the LSB and the MSB is shifted into the carry bit C Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Loaded from the MSB V A Set if an arithmetic overflow occurs the initial value is 040000h dst 0C0000h reset otherwise W Set if an arithmetic overflow occurs the initial value is 04000h dst 0C000h reset otherwise B Set if an arithme...

Страница 238: ...SB is retained and shifted into MSB 1 The LSB 1 is shifted into the LSB and the LSB is shifted into the carry bit C The word instruction RRAM W clears the bits Rdst 19 16 Note This instruction does not use the extension word Status Bits N Set if result is negative A Rdst 19 1 reset if Rdst 19 0 W Rdst 15 1 reset if Rdst 15 0 Z Set if result is zero reset otherwise C Loaded from the LSB n 1 LSB 1 n...

Страница 239: ... clears the bits Rdst 19 8 The MSB retains its value sign the LSB is shifted into the carry bit RRAX here operates equal to a signed division by 2 All other modes for the destination the destination operand is shifted right arithmetically by 1 bit position as shown in Figure 4 49 The MSB retains its value sign the LSB is shifted into the carry bit RRAX here operates equal to a signed division by 2...

Страница 240: ...Instruction Set Description www ti com 240 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX RRAX B EDE EDE 2 EDE Figure 4 48 Rotate Right Arithmetically RRAX B A Register Mode Figure 4 49 Rotate Right Arithmetically RRAX B A Non Register Mode ...

Страница 241: ...eration C MSB MSB 1 LSB 1 LSB C Description The destination operand is shifted right by 1 2 3 or 4 bit positions as shown in Figure 4 50 The carry bit C is shifted into the MSB the LSB is shifted into the carry bit The word instruction RRCM W clears the bits Rdst 19 16 Note This instruction does not use the extension word Status Bits N Set if result is negative A Rdst 19 1 reset if Rdst 19 0 W Rds...

Страница 242: ...ncorporated CPUX Example The address word in R5 is shifted right by 3 positions The MSB 2 is loaded with 1 SETC Prepare carry for MSB 2 RRCM A 3 R5 R5 R5 3 20000h Example The word in R6 is shifted right by 2 positions The MSB is loaded with the LSB The MSB 1 is loaded with the contents of the carry flag RRCM W 2 R6 R6 R6 2 R6 19 16 0 Figure 4 50 Rotate Right Through Carry RRCM W and RRCM A ...

Страница 243: ... instruction RRCX B clears the bits Rdst 19 8 The carry bit C is shifted into the MSB the LSB is shifted into the carry bit All other modes for the destination the destination operand is shifted right by 1 bit position as shown in Figure 4 52 The carry bit C is shifted into the MSB the LSB is shifted into the carry bit All addressing modes with the exception of the immediate mode are possible in t...

Страница 244: ...ction Set Description www ti com 244 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX RPT 12 RRCX W R6 R6 R6 12 R6 19 16 0 Figure 4 51 Rotate Right Through Carry RRCX B A Register Mode Figure 4 52 Rotate Right Through Carry RRCX B A Non Register Mode ...

Страница 245: ... in Figure 4 53 Zero is shifted into the MSB the LSB is shifted into the carry bit RRUM works like an unsigned division by 2 4 8 or 16 The word instruction RRUM W clears the bits Rdst 19 16 Note This instruction does not use the extension word Status Bits N Set if result is negative A Rdst 19 1 reset if Rdst 19 0 W Rdst 15 1 reset if Rdst 15 0 Z Set if result is zero reset otherwise C Loaded from ...

Страница 246: ... LSB 1 LSB C Description RRUX is valid for register mode only the destination operand is shifted right by 1 bit position as shown in Figure 4 54 The word instruction RRUX W clears the bits Rdst 19 16 The byte instruction RRUX B clears the bits Rdst 19 8 Zero is shifted into the MSB the LSB is shifted into the carry bit Status Bits N Set if result is negative A dst 19 1 reset if dst 19 0 W dst 15 1...

Страница 247: ...t SBCX B 0 dst Description The carry bit C is added to the destination operand minus 1 The previous contents of the destination are lost Status Bits N Set if result is negative reset if positive Z Set if result is zero reset otherwise C Set if there is a carry from the MSB of the result reset otherwise Set to 1 if no borrow reset if borrow V Set if an arithmetic overflow occurs reset otherwise Mod...

Страница 248: ...reset otherwise src dst C Set if there is a carry from the MSB reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOFF CPUOFF and GIE are not affected Example A 20 ...

Страница 249: ... MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if there is a carry from the MSB reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSCOF...

Страница 250: ...ister mode Rn 15 8 are swapped with Rn 7 0 When the A extension is used Rn 19 16 are unchanged When the W extension is used Rn 19 16 are cleared Other modes When the A extension is used bits 31 20 of the destination address are cleared bits 19 16 are left unchanged and bits 15 8 are swapped with bits 7 0 When the W extension is used bits 15 8 are swapped with bits 7 0 of the addressed word Status ...

Страница 251: ... High Byte High Byte Before SWPBX After SWPBX X 0 19 19 16 16 www ti com Instruction Set Description 251 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated CPUX Figure 4 57 Swap Bytes SWPBX W Register Mode Figure 4 58 Swap Bytes SWPBX W In Memory ...

Страница 252: ...ion Register mode The sign of the low byte of the operand Rdst 7 is extended into the bits Rdst 19 8 Other modes SXTX A the sign of the low byte of the operand dst 7 is extended into dst 19 8 The bits dst 31 20 are cleared SXTX W the sign of the low byte of the operand dst 7 is extended into dst 15 8 Status Bits N Set if result is negative reset otherwise Z Set if result is zero reset otherwise C ...

Страница 253: ...B 0 dst Description The destination operand is compared with zero The status bits are set according to the result The destination is not affected Status Bits N Set if destination is negative reset if positive Z Set if destination contains zero reset otherwise C Set V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example RAM byte LEO is tested PC is pointing to upper memory If it is negati...

Страница 254: ...e destination are lost Both operands may be located in the full address space Status Bits N Set if result is negative MSB 1 reset if positive MSB 0 Z Set if result is zero reset otherwise C Set if result is not zero reset otherwise carry not Zero V Set if both operands are negative before execution reset otherwise Mode Bits OSCOFF CPUOFF and GIE are not affected Example Toggle bits in address word...

Страница 255: ...ructions are instructions that support 20 bit operands but have restricted addressing modes The addressing modes are restricted to the register mode and the immediate mode except for the MOVA instruction Restricting the addressing modes removes the need for the additional extension word op code improving code density and execution time The MSP430X address instructions are listed and described in t...

Страница 256: ...evious contents of the destination are lost The source operand is not affected Status Bits N Set if result is negative Rdst 19 1 reset if positive Rdst 19 0 Z Set if result is zero reset otherwise C Set if there is a carry from the 20 bit result reset otherwise V Set if the result of 2 positive operands is negative or if the result of 2 negative numbers is positive reset otherwise Mode Bits OSCOFF...

Страница 257: ...ll addressing modes are given Immediate mode Branch to label EDE located anywhere in the 20 bit address space or branch directly to address BRA EDE MOVA imm20 PC BRA 01AA04h Symbolic mode Branch to the 20 bit address contained in addresses EXEC LSBs and EXEC 2 MSBs EXEC is located at the address PC X where X is within 32 K Indirect addressing BRA EXEC MOVA z16 PC PC Note If the 16 bit index is not...

Страница 258: ...inter it can alter the program execution due to access to the next address in the table pointed to by R5 Indirect indirect R5 BRA R5 MOVA R5 PC R5 4 Indexed mode Branch to the 20 bit address contained in the address pointed to by register R5 X for example a table with addresses starting at X R5 X points to the LSBs R5 X 2 points to the MSBs of the address X is within R5 32 K Indirect indirect R5 X...

Страница 259: ... RETA Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Examples Examples for all addressing modes are given Immediate mode Call a subroutine at label EXEC or call directly an address CALLA EXEC Start address EXEC CALLA 01AA04h Start address 01AA04h Symbolic mode Call a subroutine at the 20 bit address contained in addresses EX...

Страница 260: ...erwards by 4 The next time the software flow uses R5 as a pointer it can alter the program execution due to access to the next word address in the table pointed to by R5 Indirect indirect R5 CALLA R5 Start address at R5 R5 4 Indexed mode Call a subroutine at the 20 bit address contained in the address pointed to by register R5 X for example a table with addresses starting at X R5 X points to the L...

Страница 261: ...ck Copyright 2012 2020 Texas Instruments Incorporated CPUX 4 6 4 4 CLRA CLRA Clear 20 bit destination register Syntax CLRA Rdst Operation 0 Rdst Emulation MOVA 0 Rdst Description The destination register is cleared Status Bits Status bits are not affected Example The 20 bit value in R10 is cleared CLRA R10 0 R10 ...

Страница 262: ...positive src dst Z Set if result is zero src dst reset otherwise src dst C Set if there is a carry from the MSB reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positive source operand from a negative destination operand delivers a positive result reset otherwise no overflow Mode Bits OSC...

Страница 263: ...ration Rdst 2 Rdst Emulation SUBA 2 Rdst Description The destination register is decremented by 2 The original contents are lost Status Bits N Set if result is negative reset if positive Z Set if Rdst contained 2 reset otherwise C Reset if Rdst contained 0 or 1 set otherwise V Set if an arithmetic overflow occurs otherwise reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 20 bit v...

Страница 264: ...egative reset if positive Z Set if Rdst contained 0FFFFEh reset otherwise Set if Rdst contained 0FFFEh reset otherwise Set if Rdst contained 0FEh reset otherwise C Set if Rdst contained 0FFFFEh or 0FFFFFh reset otherwise Set if Rdst contained 0FFFEh or 0FFFFh reset otherwise Set if Rdst contained 0FEh or 0FFh reset otherwise V Set if Rdst contained 07FFFEh or 07FFFFh reset otherwise Set if Rdst co...

Страница 265: ...atus Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Examples Copy 20 bit value in R9 to R8 MOVA R9 R8 R9 R8 Write 20 bit immediate value 12345h to R12 MOVA 12345h R12 12345h R12 Copy 20 bit value addressed by R9 100h to R8 Source operand in addresses R9 100h LSBs and R9 102h MSBs MOVA 100h R9 R8 Index 32 K 2 words transferred Move ...

Страница 266: ...sses R9 LSBs and R9 2 MSBs MOVA R9 R8 R9 R8 R9 4 2 words transferred Copy 20 bit value in R8 to destination addressed by R9 100h Destination operand in addresses R9 100h LSBs and R9 102h MSBs MOVA R8 100h R9 Index 32 K 2 words transferred Move 20 bit value in R13 to 20 bit absolute addresses EDE LSBs and EDE 2 MSBs MOVA R13 EDE R13 EDE 2 words transferred Move 20 bit value in R13 to 20 bit address...

Страница 267: ...LA instruction is restored to the PC The program continues at the address following the subroutine call The SR bits SR 11 0 are not affected This allows the transfer of information with these bits Status Bits N Not affected Z Not affected C Not affected V Not affected Mode Bits OSCOFF CPUOFF and GIE are not affected Example Call a subroutine SUBR from anywhere in the 20 bit address space and retur...

Страница 268: ...n to the destination register the source is not affected Status Bits N Set if result is negative src dst reset if positive src dst Z Set if result is zero src dst reset otherwise src dst C Set if there is a carry from the MSB Rdst 19 reset otherwise V Set if the subtraction of a negative source operand from a positive destination operand delivers a negative result or if the subtraction of a positi...

Страница 269: ...ed with zero The status bits are set according to the result The destination register is not affected Status Bits N Set if destination register is negative reset if positive Z Set if destination register contains zero reset otherwise C Set V Reset Mode Bits OSCOFF CPUOFF and GIE are not affected Example The 20 bit value in R7 is tested If it is negative continue at R7NEG if it is positive but not ...

Страница 270: ...it Hardware Multiplier MPY32 Chapter 5 SLAU367P October 2012 Revised April 2020 32 Bit Hardware Multiplier MPY32 This chapter describes the 32 bit hardware multiplier MPY32 The MPY32 module is implemented in all devices Topic Page 5 1 32 Bit Hardware Multiplier MPY32 Introduction 271 5 2 MPY32 Operation 273 5 3 MPY32 Registers 285 ...

Страница 271: ...ns its activities do not interfere with the CPU activities The multiplier registers are peripheral registers that are loaded and read with CPU instructions The MPY32 supports Unsigned multiply Signed multiply Unsigned multiply accumulate Signed multiply accumulate 8 bit 16 bit 24 bit and 32 bit operands Saturation Fractional numbers 8 bit and 16 bit operation compatible with 16 bit hardware multip...

Страница 272: ...S3 SUMEXT 31 0 15 16 31 0 32 bit Demultiplexer 32 bit Multiplexer 16 bit Multiplexer 16 bit Multiplexer OP1_32 OP2_32 MPYMx MPYSAT MPYFRAC MPYC 2 Control Logic OP1 low word 32 Bit Hardware Multiplier MPY32 Introduction www ti com 272 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated 32 Bit Hardware Multiplier MPY32 Figure 5 1 ...

Страница 273: ...ration is ready in three MCLK cycles and can be read with the next instruction after writing to OP2 except when using an indirect addressing mode to access the result When using indirect addressing for the result a NOP is required before the result is ready The result of a 24 bit or 32 bit operation can be read with successive instructions after writing OP2 or OP2H starting with RES0 except when u...

Страница 274: ...iply operand bits 0 up to 15 MPYS32H Signed multiply operand bits 16 up to 31 MAC32L Unsigned multiply accumulate operand bits 0 up to 15 MAC32H Unsigned multiply accumulate operand bits 16 up to 31 MACS32L Signed multiply accumulate operand bits 0 up to 15 MACS32H Signed multiply accumulate operand bits 16 up to 31 Writing the second operand to the OP2 initiates the multiply operation Writing OP2...

Страница 275: ...OP2L until the initiated operation is completed In addition to RES0 to RES3 for compatibility with the 16 16 hardware multiplier the 32 bit result of a 8 bit or 16 bit operation is accessible through RESLO RESHI and SUMEXT In this case the result low register RESLO holds the lower 16 bits of the calculation result and the result high register RESHI holds the upper 16 bits RES0 and RES1 are identic...

Страница 276: ... Examples Examples for all multiplier modes follow All 8 8 modes use the absolute address for the registers because the assembler does not allow B access to word registers when using the labels from the standard definitions file There is no sign extension necessary in software Accessing the multiplier with a byte instruction during a signed operation automatically causes a sign extension of the by...

Страница 277: ...h multiplication is that the product of two number in the range from 1 0 to 1 0 is always in that same range 5 2 4 1 Fractional Number Mode Multiplying two fractional numbers using the default multiplication mode with MPYFRAC 0 and MPYSAT 0 gives a result with two sign bits For example if two 16 bit Q15 numbers are multiplied a 32 bit result in Q30 format is obtained To convert the result into Q15...

Страница 278: ...ce mathematical artifacts in control systems on overflow and underflow conditions The saturation mode should only be enabled when required and disabled after use The actual content of the result registers is not modified when MPYSAT 1 When the result is accessed using software the value is automatically adjusted to provide the most positive or most negative result when an overflow or underflow has...

Страница 279: ... unshifted RES1 bit15 0 MPYFRAC 1 Unshifted RES1 bit 15 0 and bit 14 1 Unshifted RES1 bit 15 1 and bit 14 0 www ti com MPY32 Operation 279 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated 32 Bit Hardware Multiplier MPY32 Table 5 6 Result Availability in Saturation Mode MPYSAT 1 Operation OP1 OP2 Result Ready in MCLK Cycles Af...

Страница 280: ...RAC MPY32CTL0 Pre load result registers to demonstrate overflow MOV 0 RES3 MOV 0 RES2 MOV 07FFFh RES1 MOV 0FA60h RES0 MOV B 050h MACS_B 8 bit signed MAC operation MOV B 012h OP2_B Start 16x16 bit operation MOV RES0 R6 R6 0FFFFh MOV RES1 R7 R7 07FFFh The result is saturated because already the result not converted into a fractional number shows an overflow The multiplication of the two positive num...

Страница 281: ... 00000h RES1 00000h RES0 00000h Yes No Yes No MPYFRAC 1 non fractional 64 bit Saturation MPYSAT 1 Yes No Yes No Perform 16 16 MAC or MACS Operation Perform MAC or MACS Operation Perform MPY or MPYS Operation MAC or MACS 32 bit Saturation 64 bit Saturation Shift 64 bit result Calculate SUMEXT based on MPYC and bit 15 of unshifted RES3 www ti com MPY32 Operation 281 SLAU367P October 2012 Revised Apr...

Страница 282: ...HI R7 R7 07FFFh The second operation gives a saturated result because the 32 bit value used for the 16 16 bit MACS operation was already saturated when the operation was started the carry bit MPYC was 0 from the previous operation but the MSB in result register RES1 is set As one can see in the flow chart the content of the result registers are saturated for multiply and accumulate operations afte...

Страница 283: ...ond result register RES1 Access multiplier 32x16 results with indirect addressing MOV RES0 R5 RES0 address in R5 for indirect MOV OPER1L MPY32L Load low word of 1st operand MOV OPER1H MPY32H Load high word of 1st operand MOV OPER2 OP2 Load 2nd operand 16 bits NOP Need one cycle MOV R5 xxx Move RES0 NOP Need one additional cycle MOV R5 xxx Move RES1 No additional cycles required MOV R5 xxx Move RES...

Страница 284: ... high word PUSH MPY32L Save operand 1 low word PUSH OP2H Save operand 2 high word PUSH OP2L Save operand 2 low word Main part of ISR Using standard MPY routines POP OP2L Restore operand 2 low word POP OP2H Restore operand 2 high word Starts dummy multiplication but result is overwritten by following restore operations POP MPY32L Restore operand 1 low word POP MPY32H Restore operand 1 high word POP...

Страница 285: ...06h MACS 16 bit operand one signed multiply accumulate Read write Word Undefined 06h MACS_L Read write Byte Undefined 07h MACS_H Read write Byte Undefined 06h MACS_B 8 bit operand one signed multiply accumulate Read write Byte Undefined 08h OP2 16 bit operand two Read write Word Undefined 08h OP2_L Read write Byte Undefined 09h OP2_H Read write Byte Undefined 08h OP2_B 8 bit operand two Read write...

Страница 286: ...ite Byte Undefined 22h OP2H 32 bit operand 2 high word Read write Word Undefined 22h OP2H_L Read write Byte Undefined 23h OP2H_H Read write Byte Undefined 22h OP2H_B 24 bit operand 2 high byte Read write Byte Undefined 24h RES0 32x32 bit result 0 least significant word Read write Word Undefined 24h RES0_L Read write Byte Undefined 26h RES1 32x32 bit result 1 Read write Word Undefined 28h RES2 32x3...

Страница 287: ...write enable All writes to any MPY32 register are delayed until the 64 bit MPYDLY32 0 or 32 bit MPYDLY32 1 result is ready 0b Writes are not delayed 1b Writes are delayed 7 MPYOP2_32 RW 0h Multiplier bit width of operand 2 0b 16 bits 1b 32 bits 6 MPYOP1_32 RW 0h Multiplier bit width of operand 1 0b 16 bits 1b 32 bits 5 4 MPYMx RW 0h Multiplier mode 00b MPY Multiply 01b MPYS Signed multiply 10b MAC...

Страница 288: ... diagram in the device specific data sheet to determine the supported FRAM controller if FRCTL_A is not specifed in the block diagram the device supports FRCTL Table 6 1 FRAM Controller Overview Feature FRCTL FRCTL_A Wait state control Automatic wait state mode No Yes User wait state mode Yes Yes Control Bits NWAITS 2 0 Control Bits NWAITS 3 0 Timing violation interrupt ACCTEIFG bit and a reset PU...

Страница 289: ...er 2012 Revised April 2020 FRAM Controller FRCTL This chapter describes the operation of the FRAM controller Topic Page 7 1 FRAM Introduction 290 7 2 FRAM Organization 290 7 3 FRCTL Module Operation 290 7 4 Programming FRAM Devices 291 7 5 Wait State Control 291 7 6 FRAM ECC 292 7 7 FRAM Write Back 292 7 8 FRAM Power Control 292 7 9 FRAM Cache 293 7 10 FRCTL Registers 294 ...

Страница 290: ...ts by the Memory Protection Unit MPU See Chapter 9 Memory Protection Unit for details The address space is linear with the exception of the User Information Memory and the Device Descriptor Information TLV 7 3 FRCTL Module Operation The FRAM can be read in a similar fashion to SRAM and needs no special requirements Similarly any writes to unprotected segments can be written in the same fashion as ...

Страница 291: ...vice through any means available for example UART or SPI User developed software can receive the data and program the FRAM Because this type of solution is developed by the user it can be completely customized to fit the application needs for programming or updating the FRAM 7 5 Wait State Control The system clock for the CPU or DMA can exceed the FRAM access and cycle time requirements For these ...

Страница 292: ...table bit error has been detected in the FRAM error detection logic UBDRSTEN can be used to enable a power up clear PUC reset or UBDIE can be used to enable an NMI event UBDRSTEN and UBDIE are mutually exclusive and are not allowed to be set simultaneously For more information refer to the MSP430 FRAM Quality and Reliability application report 7 7 FRAM Write Back All reads from FRAM requires a wri...

Страница 293: ...r 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated FRAM Controller FRCTL Figure 7 2 FRAM Power Control Diagram 7 9 FRAM Cache The FRAM controller implements a read cache to provide a speed benefit when running the CPU at higher speeds than the FRAM supports without wait states The cache implemented is a 2 way associative cache with 4 cache li...

Страница 294: ...ssword triggers a PUC A write access to a register other than FRCTL while write access is not enabled causes a PUC NOTE All registers have word or byte register access For a generic registerANYREG the suffix _L ANYREG_L refers to the lower byte of the register bits 0 through 7 The suffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 Table 7 1 FRCTL Registers Offset Acronym...

Страница 295: ...ion Bit Field Type Reset Description 15 8 FRCTLPW RW 96h FRCTLPW password Always reads as 96h To enable write access to the FRCTL registers write A5h A word write of any other value causes a PUC After a correct password is written and register access is enabled write a wrong password in byte mode to disable the access In this case no PUC is generated 7 Reserved R 0h Reserved Always reads as 0 6 4 ...

Страница 296: ...ent if uncorrectable bit error detected The bits UBDRSTEN and UBDIE are mutual exclusive and are not allowed to be set simultaneously Only one error handling can be selected at one time 0b Uncorrectable bit detection interrupt disabled 1b Uncorrectable bit detection interrupt enabled Generates vector in SYSSNIV 5 CBDIE RW 0h Enable NMI event if correctable bit error detected 0b Correctable bit det...

Страница 297: ... NWAITS In the case it is not an FRAM access violation The ACCTEIFG bit does not trigger a PUC or change the SYSRSTIV register value The ACCTEIFG bit is cleared only by writing 0 It is recommended to use SYSRESTIV register to check FRAM access violation error to avoid confusion 2 UBDIFG RW 0h FRAM uncorrectable bit error flag This interrupt flag is set if an uncorrectable bit error has been detect...

Страница 298: ...apter describes the operation of the FRAM controller A FRCTL_A The FRCTL_A and FRCTL are almost identical in terms of the features that they support For a summary of the differences between the two modules see the FRAM Controller Overview chapter Topic Page 8 1 FRAM Controller A FRCTL_A Introduction 299 8 2 FRAM Controller A FRCTL_A Operation 299 8 3 FRAM ECC 302 8 4 FRAM Power Control 302 8 5 FRA...

Страница 299: ...nded write accesses see MSP430 FRAM Technology How To and Best Practices Figure 8 1 shows the block diagram of the FRCTL_A Figure 8 1 FRCTL_A Block Diagram 8 2 FRAM Controller A FRCTL_A Operation FRAM is a nonvolatile memory that eliminates the slow writing barrier of flash memory The read and write operations of FRAM is just like the way that the standard SRAM works The FRAM features SRAM like op...

Страница 300: ... 3 1 Write Protection The WPROT bit can be used to protect the contents of FRAM from being unintentionally modified When the WPROT is set reading is allowed but no writing to FRAM memory is allowed If a write access is attempted with WPROT 1 the WPIFG write protection flag bit is set In this case the error generates a system NMI SYSNMI if the WPIE write protection interrupt enable bit is set Note ...

Страница 301: ...er to configure NWAITS 3 0 bits The value written to NWAITS 3 0 has no influence in this mode In order to determine the wait state automatically the FRAM controller A FRCTL_A adds a delay so that no maximum FRAM access speed is reached and no timing violation is guaranteed See Table 8 1 for wait state numbers in automatic mode with different system frequencies Table 8 1 FRAM memory Access Speed Sy...

Страница 302: ...cess to FRAM the FRAM goes into INACTIVE mode so that the FRAM does not consume power INACTIVE mode can be used if FRAM access is not required for a significant amount of time For example short tasks can be executed from RAM so while CPU runs from RAM FRAM can be powered off When the FRAM is in the INACTIVE mode wake up is automatic An access to FRAM read or write wakes up the FRAM before performi...

Страница 303: ...s LPM0 LPM1 LPM2 LPM3 or LPM4 AM 1 No INACTIVE ACTIVE LPM0 LPM1 LPM2 LPM3 or LPM4 AM 0 No INACTIVE INACTIVE Figure 8 2 shows the flow of the FRAM power transitions Figure 8 2 FRAM Power Control Diagram 8 5 FRAM Cache The FRAM controller A FRCTL_A has a cache that contains four 64 bit lines One of the 64 bit lines is preloaded during one access cycle and the cache can keep up to 32 bytes 4 64 bit f...

Страница 304: ...wrong password triggers a PUC A write access to a register other than FRCTL0 while write access is not enabled causes a PUC Note 1 The correct password A5h is written to the FRCTLPW bits by the bootcode during the device boot up process therefore the FRCTL0 low byte GCCTL0 and GCCTL1 registers are unlocked after the device is powered up or reset BOR or after LPMx 5 wakeup Note 2 All registers have...

Страница 305: ...state generator access time control when AUTO 0 Each wait state adds a N integer multiple increase of the IFCLK period where N 0 through 15 N 0 implies no wait states When a timing violation is detected the Access Time Error Flag ACCTEIFG is set and the maximum wait state 15 is automatically applied to the NWAITS 3 0 to avoid further timing violation While the ACCTEIFG bit is set the NWAIS 3 0 can...

Страница 306: ...ler state machine 2 1 Reserved R 0h Reserved Always read 0 Reset type PUC 0 WPROT R W 0h Write Protection Enable This bit is set after BOR This bit must be cleared before accessing FRAM for write This bit does not block read operation Note that the WPROT bit protects the entire FRAM memory from unintended write so it should be used as temporary protection If it is desired to protect a portion of t...

Страница 307: ...le bit error detection flag 1h R W UBDRSTEN_1 PUC initiated on uncorrectable bit error detection flag Generates vector in SYSRSTIV Clear the UBDIE bit 6 UBDIE R W 0h Enable NMI event for the uncorrectable bit error detection flag UBDIFG The UBDRSTEN and UBDIE must be mutual exclusive The FRAM controller does not allow the status of both bits are being set Writing 1 to one of the bits will automati...

Страница 308: ... power The INACTIVE mode can be used if no FRAM access is required for a significant amount of time Once the FRAM memory is in the INACTIVE mode wake up is automatic An access to FRAM read or write will wake up the FRAM memory before performing the access In this case the FRPWR bit is set automatically by the FRAM controller When the device enters LPM0 1 2 3 4 modes the FRAM memory also enters INA...

Страница 309: ...wait state will be automatically applied to the NWAITS 3 0 to avoid further timing violation While the ACCTEIFG bit is set the NWAIS 3 0 cannot be overwritten and the FRAM memory write access is prohibited regardless of the WPROT bit The ACCTEIFG bit must be cleared prior to applying a new value to NWAITS 3 0 or writing access to the FRAM memory The timing violation ACCTEIFG can generate a system ...

Страница 310: ... error is detected and corrected in the FRAM memory error detection logic This bit can generate a system NMI if the CBDIE bit is set see the GCCTL0 register This bit can be cleared by software or by reading the system NMI vector word SYSSNIV if it is the highest pending interrupt flag This bit is write 0 only and write 1 has no effect Reset type BOR 0h R W CBDIFG_0 No interrupt is pending 1h R W C...

Страница 311: ...ober 2012 Revised April 2020 Memory Protection Unit MPU This chapter describes the operation of the Memory Protection Unit MPU The MPU is family specific Topic Page 9 1 Memory Protection Unit MPU Introduction 312 9 2 MPU Segments 313 9 3 MPU Access Management Settings 317 9 4 MPU Violations 318 9 5 MPU Lock 318 9 6 How to Enable MPU and IPE Segments 318 9 7 MPU Registers 321 ...

Страница 312: ...ration of main memory into three variable sized segments Access rights for each segment can be set independently Fixed size constant user information memory segment with selectable access rights Protection of MPU registers by password NOTE After BOR no segmentation is initiated and the main memory and information memory are accessible by read write and execute operations For important software des...

Страница 313: ...ze Figure 9 3 and Figure 9 4 show fixed bits of the segment register when memory size is 128KB and 256KB respectively The beginning of segment 1 is the lowest available address for the main memory as defined in the device specific data sheet The lower border B1 defines the end of segment 1 and the beginning of segment 2 The higher border B2 defines the end of segment 2 and beginning of segment 3 T...

Страница 314: ...PUIPSEGB1 15 0 and MPUIPSEGB2 15 0 respectively in the MPUIPSEGBx register The position of both borders follows the same mechanism as described in for the main segments The beginning of the IP encapsulation segment IPE segment IBL is defined by the lower value of either the MPUIPSEGB1 15 0 or MPUIPSEGB2 15 0 register The end of the IPE segment IBH is defined by the higher value of either the MPUIP...

Страница 315: ...d access rights as describe in Section 9 3 are applied NOTE Code fetch from the first 8 bytes in IPE segment does not enable data access The first 8 bytes within the IPE segment do not enable data access within the IPE segment if code is executed from that area The start of an IPE segment is reserved for a data structure describing the IPE segment boundaries shows the segmentation of the main memo...

Страница 316: ...h to 013FFFh Border Address MPUSEGBx 15 0 outside 0000h outside 03C0h 04000h 0400h 04400h 0440h 04800h 0480h 04C00h 04C0h 05000h 0500h 0F000h 0F00h 0F400h 0F40h 0F800h 0F80h 0FC00h 0FC0h 10000h 1000h 10400h 1040h 13000h 1300h 13400h 1340h 13800h 1380h 13C00h 13C0h 14000h top of memory 1400h outside 1440h outside 3F80h outside 3FC0h NOTE Depending on the memory size settings for MPUSEGBx 4 0 the ca...

Страница 317: ...E MPUSEGxWE and MPUSEGxRE Not all settings lead to a different memory protection For example as shown if the execution bit MPUSEGxXE is set to 1 read access is automatically allowed independent of the setting of MPUSEGxRE Also setting the MPUSEGxWE bit to 1 enables the read option NOTE Combinations that are not shown in Table 9 4 should be avoided because they may be used in future versions of the...

Страница 318: ...n rights a violation occurs 9 4 2 Violation Handling The handling of access rights violations can be selected for each segment with the MPUSEGxVS bit in the MPUSAM register By default MPUSEGxVS 0 any access right violation causes a nonmaskable interrupt NMI Setting MPUSEGxVS 1 causes a PUC to occur In either case the illegal instruction on a protected memory segment is not executed Upon an access ...

Страница 319: ...D IPE signature valid flag IPE Signature 2 0FF8Ah IPE_STR_PTR_SRC Source for pointer nibble address to MPU IPE structure 9 6 1 1 1 Trapdoor Mechanism for IP Structure Pointer Transfer The bootcode performs a sequence to ensure the integrity of the IPE structure pointer On bootcode execution a valid IPE Signature 1 triggers the transfer of the IPE Signature 2 IPE structure pointer source to a secur...

Страница 320: ...r of IP Encapsulation segment Value is written to MPUIPSEGB1 MPUCHECK 6h word Odd bit interleaved parity NOTE Although the user is free to select the location for the IPE Init Structure protection against unwanted modification is given only if the structure is placed inside of the protected area checked by the structure itself This allows a reconfiguration from within the protected area but preven...

Страница 321: ...r bits 8 through 15 Table 9 8 MPU Registers Offset Acronym Register Name Type Access Reset Section 00h MPUCTL0 Memory Protection Unit Control 0 Read write Word 9600h Section 9 7 1 00h MPUCTL0_L Read Write Byte 00h 01h MPUCTL0_H Read Write Byte 96h 02h MPUCTL1 Memory Protection Unit Control 1 Read write Word 0000h Section 9 7 2 02h MPUCTL1_L Read Write Byte 00h 03h MPUCTL1_H Read Write Byte 00h 04h...

Страница 322: ...PUC After a correct password is written and MPU register access is enabled a wrong password write in byte mode disables the access and no PUC is generated This behavior is independent from MPULOCK bit settings 7 5 Reserved R 0h Reserved Always read 0 4 MPUSEGIE RW 0h Enable NMI Event if a Segment violation is detected in any Segment 0b Segment violation interrupt disabled 1b Segment violation inte...

Страница 323: ...his bit is cleared by software or by reading the reset vector word SYSRSTIV if it is the highest pending interrupt flag This bit is write 0 only and write 1 has no effect 0b No interrupt pending 1b Interrupt pending 2 MPUSEG3IFG RW 0h Main Memory Segment 3 Violation Interrupt Flag This bit is set if an access violation in Main Memory Segment 3 is detected This bit is cleared by software or by read...

Страница 324: ... Border 2 address line equivalents FRAM size 128KB MPUSEGB2 15 14 MPU Segment Border 2 address line 19 18 equivalents Must be written as zero MPUSEGB2 13 6 MPU Segment Border 2 address lines 17 10 After BOR the bits are set to 0 if MPU is enabled and MPUSEGB1 is also 0 only Segment 3 is active MPUSEGB2 5 0 MPU Segment Border 2 address line 9 4 equivalents Must be written as zero 128KB FRAM size 25...

Страница 325: ... Border 1 address line equivalents FRAM size 128KB MPUSEGB1 15 14 MPU Segment Border 1 address line 19 18 equivalents Must be written as zero MPUSEGB1 13 6 MPU Segment Border 1 address lines 17 10 After BOR the bits are set to 0 if MPU is enabled and MPUSEGB2 is also 0 only Segment 3 is active MPUSEGB1 5 0 MPU Segment Border 1 address line 9 4 equivalents Must be written as zero 128KB FRAM size 25...

Страница 326: ...ation Memory Segment Write Enable If set this bit enables write access on User Information Memory 0b Write on User Information Memory causes a violation 1b Write on User Information Memory is allowed 12 MPUSEGIRE RW 1h MPU User Information Memory Segment Read Enable If set this bit enables read access on User Information Memory 0b Read on User Information Memory causes a violation if MPUSEGIWE MPU...

Страница 327: ...SEG2RE RW 1h MPU Main Memory Segment 2 Read Enable If set this bit enables read access on Main Memory segment 2 0b Read on Main Memory Segment 2 causes a violation if MPUSEG2WE MPUSEG2XE 0 1b Read on Main Memory Segment 2 is allowed 3 MPUSEG1VS RW 0h MPU Main Memory Segment 1 Violation Select This bit selects if additional to the interrupt flag a PUC must be executed illegal access to Main Memory ...

Страница 328: ...capsulation Lock If this bit is set access to MPUIPC0 and MPUIPSEGBx registers is locked and they are read only until a BOR occurs BOR sets the bit to 0 0b Open 1b Locked 6 MPUIPENA RW 0h MPU IP Encapsulation Enable This bit enables the MPU IP Encapsulation operation The enable bit can be set any time with word write and a correct password if MPUIPLOCK is not set 0b Disabled 1b Enabled 5 MPUIPVS R...

Страница 329: ...t Border 2 address line equivalents FRAM size 128KB MPUIPSEGB2 15 14 MPU IP Segment Border 2 address line 19 18 equivalents Must be written as zero MPUIPSEGB2 13 6 MPU IP Segment Border 2 address lines 17 10 After BOR the bits are set to 0 if MPU is enabled and MPUSEGB1 is also 0 only Segment 3 is active MPUIPSEGB2 5 0 MPU IP Segment Border 2 address line 9 4 equivalents Must be written as zero 12...

Страница 330: ...egment Border 1 address line equivalents FRAM size 128KB MPUIPSEGB1 15 14 MPU Segment Border 1 address line 19 18 equivalents Must be written as zero MPUIPSEGB1 13 6 MPU Segment Border 1 address lines 17 10 After BOR the bits are is set to 0 if MPU is enabled and MPUSEGB2 is also 0 only Segment 3 is active MPUIPSEGB1 5 0 MPU Segment Border 1 address line 9 4 equivalents Must be written as zero 128...

Страница 331: ...struments Incorporated RAM Controller RAMCTL Chapter 10 SLAU367P October 2012 Revised April 2020 RAM Controller RAMCTL The RAM controller RAMCTL allows control of the power down behavior of the RAM Topic Page 10 1 RAM Controller RAMCTL Introduction 332 10 2 RAMCTL Operation 332 10 3 RAMCTL Registers 334 ...

Страница 332: ...d completely undefined Any potentially required re initialization must be implemented in software The RCCTL0 register is protected with a key The RCCTL0 register content can be modified only if the correct key is written during a word write Byte write accesses or write accesses with a wrong key are ignored Figure 10 1 RAM Power Mode Transitions Into and Out of LPM3 or LPM4 10 2 1 Considerations fo...

Страница 333: ...x3FFF A instruction fetch access from CPU results in executing a jump instruction 0x3FFF A read or write access from CPU or DMA causes the DACCESSIFG bit to be set This conflict does not affect the access by the DTC The DACCESS interrupt can be enabled or disabled by the DACCESSIE bit If DACCESSIE 1 and DACCESSIFG 1 then a user NMI is generated DACCESSIFG See the device specific data sheet for the...

Страница 334: ... 10 1 lists the memory mapped registers for the RAMCTL All register offset addresses not listed in Table 10 1 should be considered as reserved locations and the register contents should not be modified Table 10 1 RAMCTL Registers Offset Acronym Register Name Type Reset Section 0h CTL0 RAM Controller Control 0 read write 6900h Section 10 3 1 2h CTL1 RAM Controller Control 1 read write 0h Section 10...

Страница 335: ...sector is lost after wakeup from LPM3 and LPM4 See the device specific data sheet to find the number of available sectors the address range and the size of each RAM sector 2h R W Turns off this RAM sector entering LPM3 and LPM4 the RAM sector remains off after wake up All data of this RAM sector is lost See the devicespecific data sheet to find the number of available sectors the address range and...

Страница 336: ...M sector entering LPM3 and LPM4 the RAM sector remains off after wake up All data of this RAM sector is lost See the devicespecific data sheet to find the number of available sectors the address range and the size of each RAM sector 1 0 RS0OFF R W 0h RAM controller RAM sector 0 off 0h R W Contents of this RAM sector are retained in LPM3 and LPM4 1h R W Turns off this RAM sector in LPM3 and LPM4 re...

Страница 337: ...SS Interrupt can be enabled or disabled by DACCESSIE bit If DACCESSIE 1 and DACCESSIFG 1 then an User NMI is generated See the device speicfic datasheet for details 0h R W Disable NMI for DACCESS Interrupt 1h R W Enable NMI for DACCESS Interrupt 7 1 Reserved R 0h Reserved 0 DACCESSIFG R W 0h DACCESS Interrupt Flag LEA RAM can be accessed by CPU DMA or DTC DTC has the highest priority If CPU or DMA...

Страница 338: ...hapter 11 SLAU367P October 2012 Revised April 2020 DMA Controller The direct memory access DMA controller module transfers data from one address to another without CPU intervention This chapter describes the operation of the DMA controller Topic Page 11 1 Direct Memory Access DMA Introduction 339 11 2 DMA Operation 341 11 3 DMA Registers 353 ...

Страница 339: ...chapter are not applicable to all devices See the device specific data sheet for the number of channels that are supported Using the DMA controller can increase the throughput of peripheral modules It can also reduce system power consumption by allowing the CPU to remain in a low power mode without having to awaken to move data to or from a peripheral DMA controller features include Up to eight in...

Страница 340: ...ace NMI Interrupt Request JTAG Active Halt Halt CPU ROUNDROBIN DMARMWDIS DMAnTSEL DMA0TRIG31 DMA0TRIG0 DMA0TSEL 5 DMA0TRIG1 00000 00001 11111 DMA1TRIG31 DMA1TRIG0 DMA1TSEL 5 DMA1TRIG1 00000 00001 11111 DMAnTRIG31 DMAnTRIG0 5 DMAnTRIG1 00000 00001 11111 DMA Priority and Control Direct Memory Access DMA Introduction www ti com 340 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedbac...

Страница 341: ...ple channel 0 may transfer between two fixed addresses while channel 1 transfers between two blocks of addresses The addressing modes are shown in Figure 11 2 The addressing modes are Fixed address to fixed address Fixed address to block of addresses Block of addresses to fixed address Block of addresses to block of addresses The addressing modes are configured with the DMASRCINCR and DMADSTINCR c...

Страница 342: ...d SRCBYTE fields The source and destination locations can be either byte or word data It is also possible to transfer byte to byte word to word or any combination Table 11 1 DMA Transfer Modes DMADT Transfer Mode Description 000 Single transfer Each transfer requires a trigger DMAEN is automatically cleared when DMAxSZ transfers have been made 001 Block transfer A complete block is transferred wit...

Страница 343: ...gger The single transfer state diagram is shown in Figure 11 3 The DMAxSZ register defines the number of transfers to be made The DMADSTINCR and DMASRCINCR bits select if the destination address and the source address are incremented or decremented after each transfer If DMAxSZ 0 no transfers occur The DMAxSA DMAxDA and DMAxSZ registers are copied into temporary registers The temporary values of D...

Страница 344: ...mented or decremented after each transfer of the block If DMAxSZ 0 no transfers occur The DMAxSA DMAxDA and DMAxSZ registers are copied into temporary registers The temporary values of DMAxSA and DMAxDA are incremented or decremented after each transfer in the block The DMAxSZ register is decremented after each transfer of the block and shows the number of transfers remaining in the block When the...

Страница 345: ...DMAxSZ 0 OR DMAEN 0 DMAxSZ T_Size DMAxSA T_SourceAdd DMAxDA T_DestAdd DMAREQ 0 T_Size DMAxSZ DMAxSA T_SourceAdd DMAxDA T_DestAdd DMADT 5 AND DMAxSZ 0 AND DMAEN 1 DMAEN 0 DMAEN 1 DMAEN 0 DMAREQ 0 T_Size DMAxSZ DMAABORT 1 2 MCLK DMAEN 0 www ti com DMA Operation 345 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated DMA Controller...

Страница 346: ...ss and the source address are incremented or decremented after each transfer of the block If DMAxSZ 0 no transfers occur The DMAxSA DMAxDA and DMAxSZ registers are copied into temporary registers The temporary values of DMAxSA and DMAxDA are incremented or decremented after each transfer in the block The DMAxSZ register is decremented after each transfer of the block and shows the number of transf...

Страница 347: ...ALEVEL 1 AND Trigger 0 DMADT 2 3 AND DMAxSZ 0 OR DMAEN 0 DMAxSZ T_Size DMAxSA T_SourceAdd DMAxDA T_DestAdd T_Size DMAxSA T_SourceAdd DMAxDA T_DestAdd DMAxSZ DMAEN 0 DMAEN 1 DMAxSZ 0 DMAxSZ 0 AND a multiple of 4 words bytes were transferred DMAxSZ 0 DMAEN 0 DMAREQ 0 T_Size DMAxSZ www ti com DMA Operation 347 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 ...

Страница 348: ...e transfer mode each transfer requires its own trigger When using block or burst block modes only one trigger is required to initiate the block or burst block transfer 11 2 3 2 Level Sensitive Triggers When DMALEVEL 1 level sensitive triggers are used For proper operation level sensitive triggers can only be used when external trigger DMAE0 is selected as the trigger DMA transfers are triggered as...

Страница 349: ...XIFG does not trigger a transfer A transfer is triggered when eUSCI_Ax is ready to transmit new data UCAxTXIFG is automatically reset when the transfer starts If UCAxTXIE is set the UCAxTXIFG does not trigger a transfer eUSCI_Bx A transfer is triggered when eUSCI_Bx receives new data UCBxRXIFG is automatically reset when the transfer starts If UCBxRXIE is set the UCBxRXIFG does not trigger a trans...

Страница 350: ... Transfer DMA Cycle Time CPU Operating Mode Clock Source Maximum DMA Cycle Time Active mode MCLK DCOCLK 4 MCLK cycles Active mode MCLK LFXT1CLK 4 MCLK cycles Low power mode LPM0 or LPM1 MCLK DCOCLK 5 MCLK cycles Low power mode LPM3 or LPM4 MCLK DCOCLK 5 MCLK cycles 5 µs 1 Low power mode LPM0 or LPM1 MCLK LFXT1CLK 5 MCLK cycles Low power mode LPM3 MCLK LFXT1CLK 5 MCLK cycles Low power mode LPM4 MCL...

Страница 351: ...n The software overhead for different interrupt sources includes interrupt latency and return from interrupt cycles but not the task handling itself Interrupt handler for DMAxIFG Cycles DMA_HND Interrupt latency 6 ADD DMAIV PC Add offset to Jump table 3 RETI Vector 0 No interrupt 5 JMP DMA0_HND Vector 2 DMA channel 0 2 JMP DMA1_HND Vector 4 DMA channel 1 2 JMP DMA2_HND Vector 6 DMA channel 2 2 JMP...

Страница 352: ...ed DMA controller can automatically move data from any ADC12MEMx register to another location DMA transfers are done without CPU intervention and independently of any low power modes The DMA controller increases throughput of the ADC12 module and enhances low power applications allowing the CPU to remain off while data transfers occur DMA transfers can be triggered from any ADC12IFG flag When CONS...

Страница 353: ... 1 Transfer Size Read write Word undefined Section 11 3 9 00h DMA2CTL DMA Channel 2 Control Read write Word 0000h Section 11 3 6 02h DMA2SA DMA Channel 2 Source Address Read write Word double word undefined Section 11 3 7 06h DMA2DA DMA Channel 2 Destination Address Read write Word double word undefined Section 11 3 8 0Ah DMA2SZ DMA Channel 2 Transfer Size Read write Word undefined Section 11 3 9 ...

Страница 354: ...ess Reset Section 0Ah DMA6SZ DMA Channel 6 Transfer Size Read write Word undefined Section 11 3 9 00h DMA7CTL DMA Channel 7 Control Read write Word 0000h Section 11 3 6 02h DMA7SA DMA Channel 7 Source Address Read write Word double word undefined Section 11 3 7 06h DMA7DA DMA Channel 7 Destination Address Read write Word double word undefined Section 11 3 8 0Ah DMA7SZ DMA Channel 7 Transfer Size R...

Страница 355: ... Bit Field Type Reset Description 15 13 Reserved R 0h Reserved Always reads as 0 12 8 DMA1TSEL RW 0h DMA trigger select These bits select the DMA transfer trigger See the device specific data sheet for number of channels and trigger assignment 00000b DMA1TRIG0 00001b DMA1TRIG1 00010b DMA1TRIG2 11110b DMA1TRIG30 11111b DMA1TRIG31 7 5 Reserved R 0h Reserved Always reads as 0 4 0 DMA0TSEL RW 0h DMA t...

Страница 356: ... Bit Field Type Reset Description 15 13 Reserved R 0h Reserved Always reads as 0 12 8 DMA3TSEL RW 0h DMA trigger select These bits select the DMA transfer trigger See the device specific data sheet for number of channels and trigger assignment 00000b DMA3TRIG0 00001b DMA3TRIG1 00010b DMA3TRIG2 11110b DMA3TRIG30 11111b DMA3TRIG31 7 5 Reserved R 0h Reserved Always reads as 0 4 0 DMA2TSEL RW 0h DMA t...

Страница 357: ... Bit Field Type Reset Description 15 13 Reserved R 0h Reserved Always reads as 0 12 8 DMA5TSEL RW 0h DMA trigger select These bits select the DMA transfer trigger See the device specific data sheet for number of channels and trigger assignment 00000b DMA5TRIG0 00001b DMA5TRIG1 00010b DMA5TRIG2 11110b DMA5TRIG30 11111b DMA5TRIG31 7 5 Reserved R 0h Reserved Always reads as 0 4 0 DMA4TSEL RW 0h DMA t...

Страница 358: ... Bit Field Type Reset Description 15 13 Reserved R 0h Reserved Always reads as 0 12 8 DMA7TSEL RW 0h DMA trigger select These bits select the DMA transfer trigger See the device specific data sheet for number of channels and trigger assignment 00000b DMA7TRIG0 00001b DMA7TRIG1 00010b DMA7TRIG2 11110b DMA7TRIG30 11111b DMA7TRIG31 7 5 Reserved R 0h Reserved Always reads as 0 4 0 DMA6TSEL RW 0h DMA t...

Страница 359: ...ify write disable When set this bit inhibits any DMA transfers from occurring during CPU read modify write operations 0b DMA transfers can occur during read modify write CPU operations 1b DMA transfers inhibited during read modify write CPU operations 1 ROUNDROBIN RW 0h Round robin This bit enables the round robin DMA channel priorities 0b DMA channel priority is DMA0 DMA1 DMA2 DMA7 1b DMA channel...

Страница 360: ...nation address increments or decrements by two The DMAxDA is copied into a temporary register and the temporary register is incremented or decremented DMAxDA is not incremented or decremented 00b Destination address is unchanged 01b Destination address is unchanged 10b Destination address is decremented 11b Destination address is incremented 9 8 DMASRCINCR RW 0h DMA source increment This bit selec...

Страница 361: ...ype Reset Description 3 DMAIFG RW 0h DMA interrupt flag 0b No interrupt pending 1b Interrupt pending 2 DMAIE RW 0h DMA interrupt enable 0b Disabled 1b Enabled 1 DMAABORT RW 0h DMA abort This bit indicates if a DMA transfer was interrupt by an NMI 0b DMA transfer not interrupted 1b DMA transfer interrupted by NMI 0 DMAREQ RW 0h DMA request Software controlled DMA start DMAREQ is reset automatically...

Страница 362: ...AxSA rw rw rw rw rw rw rw rw Table 11 11 DMAxSA Register Description Bit Field Type Reset Description 31 20 Reserved R 0h Reserved Always reads as 0 19 0 DMAxSA RW undefined DMA source address The source address register points to the DMA source address for single transfers or the first source address for block transfers The source address register remains unchanged during block and burst block tr...

Страница 363: ... rw rw rw rw rw rw Table 11 12 DMAxDA Register Description Bit Field Type Reset Description 31 20 Reserved R 0h Reserved Always reads as 0 19 0 DMAxDA RW undefined DMA destination address The destination address register points to the DMA destination address for single transfers or the first destination address for block transfers The destination address register remains unchanged during block and...

Страница 364: ...w rw rw rw rw rw rw Table 11 13 DMAxSZ Register Description Bit Field Type Reset Description 15 0 DMAxSZ RW undefined DMA size The DMA size register defines the number of byte or word data per block transfer DMAxSZ register decrements with each word or byte transfer When DMAxSZ decrements to 0 it is immediately and automatically reloaded with its previously initialized value 0000h Transfer is disa...

Страница 365: ...e Reset Description 15 0 DMAIV R 0h DMA interrupt vector value 00h No interrupt pending 02h Interrupt Source DMA channel 0 Interrupt Flag DMA0IFG Interrupt Priority Highest 04h Interrupt Source DMA channel 1 Interrupt Flag DMA1IFG 06h Interrupt Source DMA channel 2 Interrupt Flag DMA2IFG 08h Interrupt Source DMA channel 3 Interrupt Flag DMA3IFG 0Ah Interrupt Source DMA channel 4 Interrupt Flag DMA...

Страница 366: ...ruments Incorporated Digital I O Chapter 12 SLAU367P October 2012 Revised April 2020 Digital I O This chapter describes the operation of the digital I O ports in all devices Topic Page 12 1 Digital I O Introduction 367 12 2 Digital I O Operation 368 12 3 I O Configuration 371 12 4 Digital I O Registers 374 ...

Страница 367: ...tain their own respective interrupt vectors Individual ports can be accessed as byte wide ports or can be combined into word wide ports and accessed by word formats Port pairs P1 and P2 P3 and P4 P5 and P6 P7 and P8 and so on are associated with the names PA PB PC PD and so on respectively All port registers are handled in this manner with this naming convention except for the interrupt vector reg...

Страница 368: ...igured as I O function input direction and the pullup or pulldown resistor are enabled the corresponding bit in the PxOUT register selects pullup or pulldown Bit 0 Pin is pulled down Bit 1 Pin is pulled up 12 2 3 Direction Registers PxDIR Each bit in each PxDIR register selects the direction of the corresponding I O pin regardless of the selected function for the pin PxDIR bits for I O pins that a...

Страница 369: ...rpose I O to the tertiary module function residing on P1 0 Initially P1SEL1 00h and P1SEL0 00h To change the function it would be necessary to write both P1SEL1 01h and P1SEL0 01h This is not possible without first passing through an intermediate configuration and this configuration may not be desirable from an application standpoint The PxSELC complement register can be used to handle such situat...

Страница 370: ... following software example shows the recommended use of P1IV and the handling overhead The P1IV value is added to the PC to automatically jump to the appropriate routine The code to handle any other PxIV register is similar The numbers at the right margin show the number of CPU cycles that are required for each instruction The software overhead for different interrupt sources includes interrupt l...

Страница 371: ... pins including unused ones Section 12 3 2 as input high impedance input with pulldown input with pullup output high or output low according to the application needs by configuring PxDIR PxREN PxOUT and PxIES accordingly This initialization takes effect as soon as the LOCKLPM5 bit in the PM5CTL register described in the PMM chapter is cleared until then the I Os remain in their high impedance stat...

Страница 372: ...ieve the lowest possible power consumption in LPMx 5 and to prevent an uncontrolled input or output I O state in the application The application has complete control of the I O pin conditions that are necessary to prevent unwanted spurious activity upon entry and exit from LPMx 5 Before entering LPMx 5 the following operations are required for the I Os a Set all I Os to general purpose I Os PxSEL0...

Страница 373: ...N PxOUT and PxIES should be restored to the values before entering LPMx 5 The LOCKLPM5 bit can then be cleared which releases the I O pin conditions and I O interrupt configuration Any changes to the port configuration registers while LOCKLPM5 is set have no effect on the I O pins After enabling the I O interrupts by configuring PxIE the I O interrupt that caused the wakeup can be serviced as indi...

Страница 374: ... Byte 00h 3Eh P4IV Port 4 Interrupt Vector Read only Word 0000h Section 12 4 1 3Eh P4IV_L Read only Byte 00h 3Fh P4IV_H Read only Byte 00h 4Eh P5IV Port 5 Interrupt Vector Read only Word 0000h Section 12 4 1 4Eh P5IV_L Read only Byte 00h 4Fh P5IV_H Read only Byte 00h 5Eh P6IV Port 6 Interrupt Vector Read only Word 0000h Section 12 4 1 5Eh P6IV_L Read only Byte 00h 5Fh P6IV_H Read only Byte 00h 6Eh...

Страница 375: ... Digital I O Table 12 3 Digital I O Registers continued Offset Acronym Register Name Type Access Reset Section 18h P1IES or PAIES_L Port 1 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Ah P1IE or PAIE_L Port 1 Interrupt Enable Read write Byte 00h Section 12 4 10 1Ch P1IFG or PAIFG_L Port 1 Interrupt Flag Read write Byte 00h Section 12 4 11 ...

Страница 376: ...PAIES_H Port 2 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Bh P2IE or PAIE_H Port 2 Interrupt Enable Read write Byte 00h Section 12 4 10 1Dh P2IFG or PAIFG_H Port 2 Interrupt Flag Read write Byte 00h Section 12 4 11 00h P3IN or PBIN_L Port 3 Input Read only Byte undefined Section 12 4 2 02h P3OUT or PBOUT_L Port 3 Output Read write Byte undefined Section 12 4 3 04h P3DIR or PBD...

Страница 377: ...PBIES_H Port 4 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Bh P4IE or PBIE_H Port 4 Interrupt Enable Read write Byte 00h Section 12 4 10 1Dh P4IFG or PBIFG_H Port 4 Interrupt Flag Read write Byte 00h Section 12 4 11 00h P5IN or PCIN_L Port 5 Input Read only Byte undefined Section 12 4 2 02h P5OUT or PCOUT_L Port 5 Output Read write Byte undefined Section 12 4 3 04h P5DIR or PCD...

Страница 378: ...PCIES_H Port 6 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Bh P6IE or PCIE_H Port 6 Interrupt Enable Read write Byte 00h Section 12 4 10 1Dh P6IFG or PCIFG_H Port 6 Interrupt Flag Read write Byte 00h Section 12 4 11 00h P7IN or PDIN_L Port 7 Input Read only Byte undefined Section 12 4 2 02h P7OUT or PDOUT_L Port 7 Output Read write Byte undefined Section 12 4 3 04h P7DIR or PDD...

Страница 379: ...PDIES_H Port 8 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Bh P8IE or PDIE_H Port 8 Interrupt Enable Read write Byte 00h Section 12 4 10 1Dh P8IFG or PDIFG_H Port 8 Interrupt Flag Read write Byte 00h Section 12 4 11 00h P9IN or PEIN_L Port 9 Input Read only Byte undefined Section 12 4 2 02h P9OUT or PEOUT_L Port 9 Output Read write Byte undefined Section 12 4 3 04h P9DIR or PED...

Страница 380: ..._H Port 10 Interrupt Edge Select Read write Byte undefined Section 12 4 9 1Bh P10IE or PEIE_H Port 10 Interrupt Enable Read write Byte 00h Section 12 4 10 1Dh P10IFG or PEIFG_H Port 10 Interrupt Flag Read write Byte 00h Section 12 4 11 00h P11IN or PFIN_L Port 11 Input Read only Byte undefined Section 12 4 2 02h P11OUT or PFOUT_L Port 11 Output Read write Byte undefined Section 12 4 3 04h P11DIR o...

Страница 381: ...Port A Resistor Enable Read write Word 0000h 06h PAREN_L Read write Byte 00h 07h PAREN_H Read write Byte 00h 0Ah PASEL0 Port A Select 0 Read write Word 0000h 0Ah PASEL0_L Read write Byte 00h 0Bh PASEL0_H Read write Byte 00h 0Ch PASEL1 Port A Select 1 Read write Word 0000h 0Ch PASEL1_L Read write Byte 00h 0Dh PASEL1_H Read write Byte 00h 16h PASELC Port A Complement Select Read write Word 0000h 16h...

Страница 382: ...Port B Resistor Enable Read write Word 0000h 06h PBREN_L Read write Byte 00h 07h PBREN_H Read write Byte 00h 0Ah PBSEL0 Port B Select 0 Read write Word 0000h 0Ah PBSEL0_L Read write Byte 00h 0Bh PBSEL0_H Read write Byte 00h 0Ch PBSEL1 Port B Select 1 Read write Word 0000h 0Ch PBSEL1_L Read write Byte 00h 0Dh PBSEL1_H Read write Byte 00h 16h PBSELC Port B Complement Select Read write Word 0000h 16h...

Страница 383: ...Port C Resistor Enable Read write Word 0000h 06h PCREN_L Read write Byte 00h 07h PCREN_H Read write Byte 00h 0Ah PCSEL0 Port C Select 0 Read write Word 0000h 0Ah PCSEL0_L Read write Byte 00h 0Bh PCSEL0_H Read write Byte 00h 0Ch PCSEL1 Port C Select 1 Read write Word 0000h 0Ch PCSEL1_L Read write Byte 00h 0Dh PCSEL1_H Read write Byte 00h 16h PCSELC Port C Complement Select Read write Word 0000h 16h...

Страница 384: ...Port D Resistor Enable Read write Word 0000h 06h PDREN_L Read write Byte 00h 07h PDREN_H Read write Byte 00h 0Ah PDSEL0 Port D Select 0 Read write Word 0000h 0Ah PDSEL0_L Read write Byte 00h 0Bh PDSEL0_H Read write Byte 00h 0Ch PDSEL1 Port D Select 1 Read write Word 0000h 0Ch PDSEL1_L Read write Byte 00h 0Dh PDSEL1_H Read write Byte 00h 16h PDSELC Port D Complement Select Read write Word 0000h 16h...

Страница 385: ...Port E Resistor Enable Read write Word 0000h 06h PEREN_L Read write Byte 00h 07h PEREN_H Read write Byte 00h 0Ah PESEL0 Port E Select 0 Read write Word 0000h 0Ah PESEL0_L Read write Byte 00h 0Bh PESEL0_H Read write Byte 00h 0Ch PESEL1 Port E Select 1 Read write Word 0000h 0Ch PESEL1_L Read write Byte 00h 0Dh PESEL1_H Read write Byte 00h 16h PESELC Port E Complement Select Read write Word 0000h 16h...

Страница 386: ...Port F Resistor Enable Read write Word 0000h 06h PFREN_L Read write Byte 00h 07h PFREN_H Read write Byte 00h 0Ah PFSEL0 Port F Select 0 Read write Word 0000h 0Ah PFSEL0_L Read write Byte 00h 0Bh PFSEL0_H Read write Byte 00h 0Ch PFSEL1 Port F Select 1 Read write Word 0000h 0Ch PFSEL1_L Read write Byte 00h 0Dh PFSEL1_H Read write Byte 00h 16h PFSELC Port F Complement Select Read write Word 0000h 16h...

Страница 387: ... Read write Byte undefined 03h PJOUT_H Read write Byte undefined 04h PJDIR Port J Direction Read write Word 0000h 04h PJDIR_L Read write Byte 00h 05h PJDIR_H Read write Byte 00h 06h PJREN Port J Resistor Enable Read write Word 0000h 06h PJREN_L Read write Byte 00h 07h PJREN_H Read write Byte 00h 0Ah PJSEL0 Port J Select 0 Read write Word 0000h 0Ah PJSEL0_L Read write Byte 00h 0Bh PJSEL0_H Read wri...

Страница 388: ...cription Bit Field Type Reset Description 15 0 PxIV R 0h Port x interrupt vector value 00h No interrupt pending 02h Interrupt Source Port x 0 interrupt Interrupt Flag PxIFG 0 Interrupt Priority Highest 04h Interrupt Source Port x 1 interrupt Interrupt Flag PxIFG 1 06h Interrupt Source Port x 2 interrupt Interrupt Flag PxIFG 2 08h Interrupt Source Port x 3 interrupt Interrupt Flag PxIFG 3 0Ah Inter...

Страница 389: ...ter Figure 12 3 PxOUT Register 7 6 5 4 3 2 1 0 PxOUT rw rw rw rw rw rw rw rw Table 12 6 PxOUT Register Description Bit Field Type Reset Description 7 0 PxOUT RW Undefined Port x output When I O configured to output mode 0b Output is low 1b Output is high When I O configured to input mode and pullups pulldowns enabled 0b Pulldown selected 1b Pullup selected 12 4 4 PxDIR Register Port x Direction Re...

Страница 390: ...ion Bit Field Type Reset Description 7 0 PxSEL0 RW 0h Port function selection Each bit corresponds to one channel on Port x The values of each bit position in PxSEL1 and PxSEL0 are combined to specify the function For example if P1SEL1 5 1 and P1SEL0 5 0 then the secondary module function is selected for P1 5 See PxSEL1 for the definition of each value 12 4 7 PxSEL1 Register Port x Function Select...

Страница 391: ...rresponding bits in both PxSEL1 and PxSEL0 are both changed at the same time Always reads as 0 12 4 9 PxIES Register Port x Interrupt Edge Select Register Figure 12 9 PxIES Register 7 6 5 4 3 2 1 0 PxIES rw rw rw rw rw rw rw rw Table 12 12 PxIES Register Description Bit Field Type Reset Description 7 0 PxIES RW Undefined Port x interrupt edge select 0b PxIFG flag is set with a low to high transiti...

Страница 392: ...ments Incorporated Digital I O 12 4 11 PxIFG Register Port x Interrupt Flag Register Figure 12 11 PxIFG Register 7 6 5 4 3 2 1 0 PxIFG rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 12 14 PxIFG Register Description Bit Field Type Reset Description 7 0 PxIFG RW Undefined Port x interrupt flag 0b No interrupt is pending 1b Interrupt is pending ...

Страница 393: ...corporated Capacitive Touch I O Chapter 13 SLAU367P October 2012 Revised April 2020 Capacitive Touch I O This chapter describes the functionality of the Capacitive Touch I Os and related control Topic Page 13 1 Capacitive Touch I O Introduction 394 13 2 Capacitive Touch I O Operation 395 13 3 CapTouch Registers 396 ...

Страница 394: ... Instruments Incorporated Capacitive Touch I O 13 1 Capacitive Touch I O Introduction The Capacitive Touch I O module allows implementation of a simple capacitive touch sense application The module uses the integrated pullup and pulldown resistors and an external capacitor to form an oscillator by feeding back the inverted input voltage sensed by the input Schmitt triggers to the pullup and pulldo...

Страница 395: ...the Capacitive Touch I O module Figure 13 2 Capacitive Touch I O Block Diagram 13 2 Capacitive Touch I O Operation Enable the Capacitive Touch I O functionality with CAPTIOEN 1 and select a port pin using CAPTIOPOSELx and CAPTIOPISELx The selected port pin is switched into the Capacitive Touch state and the resulting oscillating signal is provided to be measured by a timer The connected timers are...

Страница 396: ...s of each Capacitive Touch I O module can be found in the device specific data sheet NOTE All registers have word or byte register access For a generic register ANYREG the suffix _L ANYREG_L refers to the lower byte of the register bits 0 through 7 The suffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 Table 13 1 CapTouch Registers Offset Acronym Register Name Type Acces...

Страница 397: ...abled 0b Current state 0 or Capacitive Touch I O is disabled 1b Current state 1 8 CAPTIOEN RW 0h Capacitive Touch I O enable 0b All Capacitive Touch I Os are disabled Signal toward timers is 0 1b Selected Capacitive Touch I O is enabled 7 4 CAPTIOPOSELx RW 0h Capacitive Touch I O port select Selects port Px Selecting a port pin that is not available on the device in use gives unpredictable results...

Страница 398: ...2012 Revised April 2020 AES256 Accelerator The AES256 accelerator module performs Advanced Encryption Standard AES encryption or decryption in hardware It supports key lengths of 128 bits 192 bits and 256 bits This chapter describes the AES256 accelerator Topic Page 14 1 AES Accelerator Introduction 399 14 2 AES Accelerator Operation 400 14 3 AES Accelerator Registers 417 ...

Страница 399: ...rding to the advanced encryption standard AES FIPS PUB 197 in hardware The AES accelerator features are AES encryption 128 bit in 168 cycles 192 bit in 204 cycles 256 bit in 234 cycles AES decryption 128 bit in 168 cycles 192 bit in 206 cycles 256 bit in 234 cycles On the fly key expansion for encryption and decryption Offline key generation for decryption Shadow register storing the initial key f...

Страница 400: ...ndkey decryption is performed 168 01 AES192 with last roundkey decryption is performed 206 10 AES256 with last roundkey decryption is performed 234 The execution time of the different modes of operation is shown in Table 14 1 While the AES module is operating the AESBUSY bit is 1 As soon as the operation has finished the AESRDYIFG bit is set Internally the AES algorithm s operations are performed ...

Страница 401: ...mplete module is reset except for AESRDYIE AESOPx and AESKLx 14 2 1 Load the Key 128 Bit 192 Bit or 256 Bit Key Length The key can be loaded by writing to the AESAKEY register or by setting AESKEYWR Depending on the selected key length AESKLx a different number of bits must be loaded If AESKLx 00 the 128 bit key must be loaded using either 16 byte writes or 8 word writes to AESAKEY If AESKLx 01 th...

Страница 402: ...writing the last byte or word of the state using AESAXIN does not start encryption or decryption 14 2 3 Read the Data 128 Bit State The state can be read if AESBUSY 0 using 16 byte reads or 8 word reads from AESADOUT When all 16 bytes are read the AESDOUTRD flag indicates completion 14 2 4 Trigger an Encryption or Decryption The AES module s encrypt or decrypt operations are triggered if the state...

Страница 403: ...1 Set AESOPx 00 to select encryption Changing the AESOPx bits clears the AESKEYWR flag and a new key must be loaded in the next step 2 Load the key as described in Section 14 2 1 3 Load the state data as described in Section 14 2 2 After the data is loaded the AES module starts the encryption 4 After the encryption is ready the result can be read from AESADOUT as described in Section 14 2 3 5 To e...

Страница 404: ...ded in the AESAKEY register Figure 14 4 AES Decryption Process Using AESOPx 01 for 128 Bit Key The steps to perform decryption are 1 Set AESOPx 01 to select decryption using the same key used for encryption Set AESOPx 11 if the first round key required for decryption the last roundkey is already generated and will be loaded in step 2 Changing the AESOPx bits clears the AESKEYWR flag and a new key ...

Страница 405: ... for 128 bit Key To generate the decryption key independent from the actual decryption 1 Set AESOPx 10 to select decryption key generation Changing the AESOPx bits clears the AESKEYWR flag and a new key must be loaded in step 2 2 Load the key as described in Section 14 2 1 The generation of the first round key required for decryption is started immediately 3 While the AES module is performing the ...

Страница 406: ...peration on the provided data An interrupt request is generated if AESRDYIE and GIE are also set AESRDYIFG is automatically reset if the AES interrupt is serviced if AESADOUT is read or if AESADIN or AESAKEY are written AESRDYIFG is reset after a PUC or with AESSWRST 1 AESRDYIE is reset after a PUC but is not reset by AESSWRST 1 14 2 11 DMA Operation and Implementing Block Cipher Modes DMA operati...

Страница 407: ...gger 1 was served the last time set again until 128 bit are written to AESAXDIN 11 CFB 00 encryption Set after encryption ready set again until 128 bit are written to AESAXIN Set after AES trigger 0 was served the last time set again until 128 bit are read from AESADOUT not set 01 or 11 decryption Set after decryption ready set again until 128 bit are written to AESAXIN Set after AES trigger 0 was...

Страница 408: ...on To implement the ECB encryption without CPU interaction two DMA channels are needed Static DMA priorities must be enabled The DMA triggers must be configured as level sensitive triggers Table 14 3 AES and DMA Configuration for ECB Encryption AES CMEN AES CMx AES OPx DMA_A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 1 00 00 Read ciphertext from AESADOUT Write plaintext to AESADIN...

Страница 409: ..._A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 1 00 01 or 11 Read plaintext from AESADOUT Write ciphertext to AESADIN which also triggers the next decryption The following pseudo code snippet shows the implementation of the ECB decryption in software ECB_Decryption key plaintext ciphertext num_blocks Pseudo Code Generate Decrypt Key Configure AES AESCMEN 0 AESOPx 10 Write key into ...

Страница 410: ...thout CPU interaction two DMA channels are needed Static DMA priorities must be enabled The DMA triggers must be configured as level sensitive triggers Table 14 5 AES and DMA Configuration for CBC Encryption AES CMEN AES CMx AES OPx DMA_A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 1 01 00 Read ciphertext from AESADOUT Write plaintext to AESAXDIN which also triggers the next encryp...

Страница 411: ...N AES CMx AES OPx DMA_A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 DMA_C Triggered by AES trigger 2 1 01 01 or 11 Write the previous ciphertext block to AESAXIN Read plaintext from AESADOUT Write next plaintext to AESADIN which also triggers the next decryption The following pseudo code snippet shows the implementation of the CBC decryption in software CBC_Decryption key IV plaint...

Страница 412: ...67P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated AES256 Accelerator Source ciphertext Destination AESAXIN Size num_blocks 1 8 words Single Transfer mode End of decryption DMA1IFG 1 ...

Страница 413: ...ption AES CMEN AES CMx AES OPx DMA_A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 DMA_C Triggered by AES trigger 2 1 10 00 Write the plaintext of the current block to AESAXIN Read ciphertext from AESADOUT Write the plaintext of the current block to AESAXDIN which also triggers the next encryption The following pseudo code snippet shows the implementation of the OFB encryption in sof...

Страница 414: ...S trigger 0 DMA_B Triggered by AES trigger 1 DMA_C Triggered by AES trigger 2 1 10 01 or 11 1 Write the ciphertext of the current block to AESAXIN Read plaintext from AESADOUT Write the ciphertext of the current block to AESAXDIN which also triggers the next encryption The following pseudo code snippet shows the implementation of the OFB decryption in software OFB_Decryption Key IV plaintext ciphe...

Страница 415: ...onfigured as level sensitive triggers Table 14 9 AES and DMA Configuration for CFB Encryption AES CMEN AES CMx AES OPx DMA_A Triggered by AES trigger 0 DMA_B Triggered by AES trigger 1 1 11 00 Write the plaintext of the current block to AESAXIN Read the ciphertext from AESADOUT which also triggers the next encryption The following pseudo code snippet shows the implementation of the CFB encryption ...

Страница 416: ...r 0 DMA_B Triggered by AES trigger 1 DMA_C Triggered by AES trigger 2 1 11 01 or 11 1 Write the ciphertext of the current block to AESAXIN Read the plaintext from AESADOUT Write the ciphertext of the current block to AESADIN which also triggers the next encryption The following pseudo code snippets shows the implementation of the CFB encryption and decryption in software CFB_Decryption Key IV plai...

Страница 417: ...ble 14 11 AES256 Registers Offset Acronym Register Name Type Access Reset Section 00h AESACTL0 AES accelerator control register 0 Read write Word 00h Section 14 3 1 02h AESACTL1 AES accelerator control register 1 Read write Word 00h Section 14 3 2 04h AESASTAT AES accelerator status register Read only Word 00h Section 14 3 3 06h AESAKEY AES accelerator key register Read write Word 00h Section 14 3...

Страница 418: ...G RW 0h AES error flag AESAKEY or AESADIN were written while an AES operation was in progress The bit must be cleared by software 0b No error 1b Error occurred 10 9 Reserved R 0h Reserved 8 AESRDYIFG RW 0h AES ready interrupt flag Set when the selected AES operation was completed and the result can be read from AESADOUT Automatically cleared when AESADOUT is read or AESAKEY or AESADIN is written 0...

Страница 419: ...Register Description continued Bit Field Type Reset Description 1 0 AESOPx RW 0h AES operation The AESOPx bits are not reset by AESSWRST 1 Writes are ignored when AESCMEN 1 and AESBLKCNTx 0 00b Encryption 01b Decryption The provided key is the same key used for encryption 10b Generate first round key required for decryption 11b Decryption The provided key is the first round key required for decryp...

Страница 420: ...r0 r0 r0 7 6 5 4 3 2 1 0 AESBLKCNTx rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Writes are ignored when AESCMEN 1 and AESBLKCNTx 0 Table 14 13 AESACTL1 Register Description Bit Field Type Reset Description 15 8 Reserved R 0h Reserved Always reads 0 7 0 AESBLKCNTx RW 0h Cipher Block Counter Number of blocks to be encrypted or decrypted with block cipher modes enabled AESCMEN 1 Ignored if AESCMEN 0 The ...

Страница 421: ...s were written 3 AESDOUTRD R 0h All 16 bytes read from AESADOUT AESDOUTRD is reset by PUC AESSWRST an error condition changing AESOPx changing AESKLx when the AES accelerator is busy and when the output data is read again 0 Not all bytes read 1 All bytes read 2 AESDINWR RW 0h All 16 bytes written to AESADIN AESAXDIN or AESAXIN Changing its state by software also resets the AESDINCNTx bits AESDINWR...

Страница 422: ...4 3 2 1 0 AESKEY0x w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 Table 14 15 AESAKEY Register Description Bit Field Type Reset Description 15 8 AESKEY1x W 0h AES key byte n 1 when AESAKEY is written as word Do not use these bits for byte access Do not mix word and byte access Always reads as zero The key is reset by PUC or by AESSWRST 1 7 0 AESKEY0x W 0h AES key byte n when AESAKEY is written as word AES next k...

Страница 423: ... 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 7 6 5 4 3 2 1 0 AESDIN0x w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 Table 14 16 AESADIN Register Description Bit Field Type Reset Description 15 8 AESDIN1x W 0h AES data in byte n 1 when AESADIN is written as word Do not use these bits for byte access Do not mix word and byte access Always reads as zero 7 0 AESDIN0x W 0h AES data in byte n when AESADIN is written as word AES ne...

Страница 424: ...2 11 10 9 8 AESDOUT1x r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 AESDOUT0x r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 Table 14 17 AESADOUT Register Description Bit Field Type Reset Description 15 8 AESDOUT1x R 0h AES data out byte n 1 when AESADOUT is read as word Do not use these bits for byte access Do not mix word and byte access 7 0 AESDOUT0x R 0h AES data out byte n when AESADOUT is read as word AE...

Страница 425: ...w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 7 6 5 4 3 2 1 0 AESXDIN0x w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 Table 14 18 AESAXDIN Register Description Bit Field Type Reset Description 15 8 AESXDIN1x W 0h AES data in byte n 1 when AESAXDIN is written as word Do not use these bits for byte access Do not mix word and byte access Always reads as zero 7 0 AESXDIN0x W 0h AES data in byte n when AESAXDIN is written as word...

Страница 426: ...ESXIN1x w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 7 6 5 4 3 2 1 0 AESXIN0x w 0 w 0 w 0 w 0 w 0 w 0 w 0 w 0 Table 14 19 AESAXIN Register Description Bit Field Type Reset Description 15 8 AESXIN1x W 0h AES data in byte n 1 when AESAXIN is written as word Do not use these bits for byte access Do not mix word and byte access Always reads as zero 7 0 AESXIN0x W 0h AES data in byte n when AESAXIN is written as wo...

Страница 427: ...67P October 2012 Revised April 2020 CRC Module The cyclic redundancy check CRC module provides a signature for a given data sequence This chapter describes the operation and use of the CRC module Topic Page 15 1 Cyclic Redundancy Check CRC Module Introduction 428 15 2 CRC Standard and Bit Order 428 15 3 CRC Checksum Generation 429 15 4 CRC Registers 432 ...

Страница 428: ... x5 1 10 Figure 15 1 LFSR Implementation of CRC CCITT Standard Bit 0 is the MSB of the Result Identical input data sequences result in identical signatures when the CRC is initialized with a fixed seed value whereas different sequences of input data in general result in different signatures 15 2 CRC Standard and Bit Order The definitions of the various CRC standards were done in the era of main fr...

Страница 429: ...tical behavior as the LFSR approach after 8 bits of data are shifted in when the LSB is shifted in first The generation of a signature calculation has to be started by writing a seed to the CRCINIRES register to initialize the register Software or hardware for example the DMA can transfer data to the CRCDI or CRCDIRB register for example from memory The value in CRCDI or CRCDIRB is then included i...

Страница 430: ...strates the operation of the on chip CRC Example 15 1 General Assembler Example PUSH R4 Save registers PUSH R5 MOV StartAddress R4 StartAddress EndAddress MOV EndAddress R5 MOV INIT CRCINIRES INIT to CRCINIRES L1 MOV R4 CRCDI Item to Data In register CMP R5 R4 End address reached JLO L1 No MOV Check_Sum CRCDI Yes Include checksum TST CRCINIRES Result 0 JNZ CRC_ERROR No CRCRES 0 error Yes CRCRES 0 ...

Страница 431: ... 03433h CRCDI 3 4 mov w 03635h CRCDI 5 6 mov w 03837h CRCDI 7 8 mov b 039h CRCDI_L 9 cmp 089F6h CRCINIRES compare result CRCRESR contains 06F91h jeq Success no error br Error to error handler mov 0FFFFh CRCINIRES initialize CRC mov b 00031h CRCDIRB_L 1 mov b 00032h CRCDIRB_L 2 mov b 00033h CRCDIRB_L 3 mov b 00034h CRCDIRB_L 4 mov b 00035h CRCDIRB_L 5 mov b 00036h CRCDIRB_L 6 mov b 00037h CRCDIRB_L...

Страница 432: ...ffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 Table 15 1 CRC Registers Offset Acronym Register Name Type Access Reset Section 00h CRCDI CRC Data In Read write Word 0000h Section 15 4 1 00h CRCDI_L Read write Byte 00h 01h CRCDI_H Read write Byte 00h 02h CRCDIRB CRC Data In Reverse Byte Read write Word 0000h Section 15 4 2 02h CRCDIRB_L Read write Byte 00h 03h CRCDIRB_H...

Страница 433: ... written to the CRCDI register is included to the present signature in the CRCINIRES register according to the CRC CCITT standard 15 4 2 CRCDIRB Register CRC Data In Reverse Register Figure 15 4 CRCDIRB Register 15 14 13 12 11 10 9 8 CRCDIRB rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 CRCDIRB rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 15 3 CRCDIRB Register Description Bit Field Type...

Страница 434: ...ister holds the current CRC result according to the CRC CCITT standard Writing to this register initializes the CRC calculation with the value written to it The value just written can be read from CRCINIRES register 15 4 4 CRCRESR Register CRC Reverse Result Register Figure 15 6 CRCRESR Register 15 14 13 12 11 10 9 8 CRCRESR r 1 r 1 r 1 r 1 r 1 r 1 r 1 r 1 7 6 5 4 3 2 1 0 CRCRESR r 1 r 1 r 1 r 1 r...

Страница 435: ...7P October 2012 Revised April 2020 CRC32 Module The 16 bit or 32 bit cyclic redundancy check CRC32 module provides a signature for a given data sequence This chapter describes the operation and use of the CRC32 module Topic Page 16 1 Cyclic Redundancy Check CRC32 Module Introduction 436 16 2 CRC Checksum Generation 436 16 3 CRC32 Register Descriptions 439 ...

Страница 436: ...10 x8 x7 x5 x4 x2 x 1 Figure 16 2 LFSR Implementation of CRC32 ISO3309 as Defined in Standard Bit 0 is MSB Identical input data sequences result in identical signatures when the CRC is initialized with a fixed seed value Different sequences of input data in general result in different signatures for a given CRC function The CRC32 module supports 16 bit and 32 bit CRC generation They are independen...

Страница 437: ... whole set of input bits is performed For this calculation the CPU or the DMA can write to the memory mapped data input registers After the last value is written to CRC16DI or CRC32DIRB the signature can be read from the CRC16INIRES or CRC32INIRES registers The CRC16 and CRC32 generators accept byte and word wide access to the input registers CRC16DI and CRC32DI For bit reversed conventions write ...

Страница 438: ... br Error to error handler mov 0FFFFh CRCINIRES initialize CRC mov w 03231h CRCDI 1 2 mov w 03433h CRCDI 3 4 mov w 03635h CRCDI 5 6 mov w 03837h CRCDI 7 8 mov b 039h CRCDI_L 9 cmp 089F6h CRCINIRES compare result CRCRESR contains 06F91h jeq Success no error br Error to error handler mov 0FFFFh CRCINIRES initialize CRC mov b 00031h CRCDIRB_L 1 mov b 00032h CRCDIRB_L 2 mov b 00033h CRCDIRB_L 3 mov b ...

Страница 439: ...DIRBB0 byte 00h 000Ah CRC32INIRESW1 CRC32 Initialization and Result read write word FFFFh Section 16 3 1 6 0008h CRC32INIRESW0 word FFFFh Section 16 3 1 5 000Bh CRC32RESB3 byte FFh 000Ah CRC32RESB2 byte FFh 0009h CRC32RESB1 byte FFh 0008h CRC32RESB0 byte FFh 000Ch CRC32RESRW1 CRC32 Result Reverse read write word FFFFh Section 16 3 1 8 000Eh CRC32RESRW0 word FFFFh Section 16 3 1 7 000Ch CRC32RESRB3...

Страница 440: ...on 15 0 CRC32DIW0 RW 0h CRC32 data in word 0 Data written to the CRC32DILW0 register is included to the present signature in the CRC32INIRES register according to the CRC32 ISO3309 standard 16 3 1 2 CRC32DIW1 Register Data Input Register Word_1 for 32 Bit CRCs Data written to this register is taken into CRC32 signature calculations This register can be accessed 8 bit wide and 16 bit wide Figure 16...

Страница 441: ...CRC32 data in word 0 as bit reversed pattern Data written to the CRC32DIRBW0 register is included to the present signature in the CRC32INIRES register according to the CRC32 ISO3309 standard 16 3 1 4 CRC32DIRBW1 Register Data In Register Word_1 with Reversed Bit Order for 32 Bit CRCs Data written to this register is taken into CRC32 signature calculations This register can be accessed 8 bit wide a...

Страница 442: ...ten to the CRC32INIRESW0 register is used as the seed for the CRC calculation according to the CRC32 ISO3309 standard Reading this register returns the current result of the CRC calculation 16 3 1 6 CRC32INIRESW1 Register Data Initialization and Result Register Word_1 for 32 Bit CRCs Data written to this register represents the seed for the CRC calculation This register always reflects the latest ...

Страница 443: ...ization and result word0 This register holds the current CRC32 result according to the CRC32 ISO3309 standard The order of bits is reverse to the order of bits in the CRC32INIRESW1 register 16 3 1 8 CRC32RESRW1 Register Data Result Register Word1 as Bit Reversed for 32 Bit CRCs Data written to this register represents the seed for the CRC calculation This register always reflects the latest signat...

Страница 444: ...to the CRC16DIW0 register is included to the present signature in the CRC16INIRES register according to the CRC16 CCITT standard 16 3 1 10 CRC16DIRBW0 Register Data In Register with Reversed Bit Order for 16 Bit CRCs Data written to this register is taken into CRC16 signature calculations This register can be accessed 8 bit wide and 16 bit wide Figure 16 12 CRC16DIRBW0 Register 15 14 13 12 11 10 9...

Страница 445: ...C16INIRESW0 RW FFh CRC16 initialization and result This register holds the current CRC16 result according to the CRC16 CCITT standard Writing to this register initializes the CRC16 calculation with the value written to it 16 3 1 12 CRC16RESRW0 Register Data Result Register with Reversed Bits for 16 Bit CRCs Data written to this register represents the seed for the CRC calculation This register alw...

Страница 446: ...r LEA for Signal Processing Chapter 17 SLAU367P October 2012 Revised April 2020 Low Energy Accelerator LEA for Signal Processing The LEA low energy accelerator module is an execution unit for vector based signal processing operations This chapter introduces the LEA Topic Page 17 1 LEA Introduction 447 17 2 LEA Operation 447 17 3 LEA Registers 449 ...

Страница 447: ...the CPU or other processors see Benchmarking the Signal Processing Capabilities of the Low Energy Accelerator on MSP430 MCUs Figure 17 1 LEA System Block Diagram 17 2 LEA Operation The LEA begins executing the selected operation when the CPU writes a LEA command to the LEA command register when the LEA is in idle mode Before writing the command the CPU must configure the LEA argument registers wit...

Страница 448: ... registers The Digital Signal Processing DSP Library for MSP Microcontrollers offers easy to use APIs that use the functions of the LEA and provide a high level environment to use the LEA in various applications The DSP Library is a set of highly optimized API functions to perform many common signal processing operations on fixed point numbers for MSP430 microcontrollers The APIs automatically ena...

Страница 449: ... Version Digital Signal Processing DSP Library for MSP Microcontrollers 1 20 00 xx or later MSP430Ware 3 60 or later 17 2 3 Where to Start 1 Read an introduction to LEA in Setting a new standard for MCU performance while minimizing energy consumption 2 See Low Energy Accelerator LEA Frequently Asked Questions FAQ for the questions about the LEA 3 See the DSP Library API Guide and DSP Library Examp...

Страница 450: ...ments Incorporated Ultrasonic Sensing Solution USS USS_A Chapter 18 SLAU367P October 2012 Revised April 2020 Ultrasonic Sensing Solution USS USS_A This chapter describes the operation of the USS and the USS_A module Topic Page 18 1 Introduction 451 18 2 Operation of the USS Module 452 18 3 Debug Features 457 ...

Страница 451: ...DHS for details The submodules have different roles and together they enable high precision data acquisition for ultrasonic technology in various applications The USS module has a dedicated power management module UUPS which generates operating voltage reference voltages and reference currents for other submodules The USS module also has a dedicated clock module HSPLL which generates a very low ji...

Страница 452: ...7P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Ultrasonic Sensing Solution USS USS_A Figure 18 1 USS and USS_A Block Diagram NOTE Naming convention for register names and bit fields ModuleName RegisterName or ModuleName RegisterName BitField 18 2 Operation of the USS Module This section describes how the USS submodules are connec...

Страница 453: ...RC 0 1 SDHS_PWR_UP DOWN SDHSCTL3 TRIGEN AUTO_START SDHS Sigma Delta ADC high speed UUPSCTL USSSWRST ASQ_LPBE UUPS_SWRST www ti com Operation of the USS Module 453 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Ultrasonic Sensing Solution USS USS_A Figure 18 2 USS and USS_A Submodule Connections NOTE In Figure 18 2 the contr...

Страница 454: ... 0 SAPHOSEL PCH0SEL 1 SAPHOSEL PCH1SEL 1 Drive output drivers to GND on mode changes SAPHOSEL PCH0SEL 0 SAPHOSEL PCH1SEL 0 SAPHBCTL ASQBSW 1 Tx bias Rx bias control on mode changes SAPHBCTL ASQBSW 0 SAPHPGCTL PGSEL 1 Select output channel in PPG on mode changes SAPHPGCTL PGSEL 0 SAPHPGCTL TRSEL 1 Trigger PPG on mode changes SAPHPGCTL TRSEL 0 SAPHICTL0 MUXCTL 1 Input channel selection on mode chang...

Страница 455: ... the all USS submodules are kept in reset state Set UUPSCTL SWRST 0 to release reset and put the module into operation mode The operation mode has to be selected before the USS is powered up For Auto mode and Register Mode set SAPGMCNF LPBE 0 To select Low Power Bias Mode set SAPHMCNF LPBE 1 SAPHMCNF LPBE shall only be changed while the PSQ is in OFF state USS_SWRST SW reset signal fo all USS subm...

Страница 456: ...d then stay in READY state Emergency measurement stop control signals While the USS module is active the current measurement sequence can be stopped at any time PSQ_STOP PSQ to ASQ to stop the current measurement immediately when UUPSCTL USSSTOP 1 or UUPSCTL USSPWRDN 1 ASQ_PPGSTOP ASQ to PPG to stop pulse generation if the PPG is active ASQ_SDHSSTOP ASQ to SDHS to stop the data conversion and turn...

Страница 457: ...r off PSQ_STOP 1 ASQ_PDREQ PSQ USS power down PSQ can receive a new USS_PWRREQ signal If SAPHASCTL1 ESOFF 1 and SAPHASCTL1 STDBY 0 when SDHS_ACQDONE 1 ASQ_STDBYREQ USS standby USS power down PSQ can receive a new USS_PWRREQ signal If SAPHASCTL1 ESOFF 1 and SAPHASCTL1 STDBY 1 when SDHS_ACQDONE 1 ASQ_ACQDONE PSQ can receive a new USS_PWRREQ signal SDHS_ACQDONE 1 SDHS SDHS_ACQDONE ASQ Signal to ASQ t...

Страница 458: ...y UUPS Chapter 19 SLAU367P October 2012 Revised April 2020 Universal USS Power Supply UUPS This chapter describes the operation of the UUPS module Topic Page 19 1 Introduction 459 19 2 USS Power up Sequence 460 19 3 USS Power States 461 19 4 Interface to the ASQ Acquisition Sequencer 463 19 5 Interrupts 466 19 6 Debug Mode 466 19 7 UUPS Registers 467 ...

Страница 459: ... UUPS 19 1 Introduction The Universal USS Power Supply UUPS is one of the submodules in the Ultrasonic Sensing Solution USS module The USS module is designed for ADC based ultrasonic sensing technology in various measurement applications Figure 19 2 shows the block diagram of the USS module Figure 19 1 USS USS_A Block Diagram The UUPS module consists of three blocks the power sequencer PSQ the ref...

Страница 460: ...from four different sources When UUPSCTL USSPWRUPSEL 0 writing 1 to UUPSCTL USSPWRUP generates the USS_PWRREQ signal and starts the USS power up sequences The other sources may or may not be available see the device specific data sheet for the internal signal sources search for UUPSCTL USSPWRUPSEL The power states of the USS module can be monitored by reading UUPSCTL UPSTATE The order of the USS p...

Страница 461: ...owing power states are supported by the UUPS module OFF The USS module is powered off UUPSCTL UPSTATE 0 TRANSITION The USS module is in transition state UUPSCTL UPSTATE 2 READY The USS module is fully powered up and ready UUPSCTL UPSTATE 3 STANDBY The USS module is powered off but the SREF remains on for fast wakeup UUPSCTL UPSTATE 1 TIMEOUT The power up sequence is taking more than expected time ...

Страница 462: ...ransitions Table 19 2 USS Power States and State Changes Current Power State Next State UUPSCTL UPSTATE Trigger Signal OFF READY 0 2 3 USS_PWREQ 0 1 READY STANDBY 3 2 1 ASQ_STDBYREQ 0 1 generated by ASQ READY OFF 3 2 0 ASQ_PDREQ 0 1 generated by ASQ READY OFF 3 2 0 UUPSCTL USSPWRDN 0 1 STANDBY OFF 1 2 0 UUPSCTL USSPWRDN 0 1 STANDBY READY 1 2 3 USS_PWRREQ 0 1 The USS power state and the device powe...

Страница 463: ...odule and generate PSQ_START to the ASQ if UUPSCTL ASQEN 1 Trigger one of the sources selected by UUPSCTL USSPWRUPSEL PSQ_START ASQ to start a new measurement process if SAPHASCTL0 TRIGSEL 1 UUPSCTL UPSTATE 0 2 3 and UUPSCTL ASQEN 1 PSQ_STOP ASQ to stop the current measurement process UUPSCTL USSSTOP 0 1 ASQ_ACQDONE Acknowledge PSQ that ASQ has completed the measurements The measurements have been...

Страница 464: ...triggered by writing 1 to SAPHASQTRIG ASQTRIG No UUPSCTL ASQEN 0 SAPHASCTL0 TRIGSEL 0 The ASQ is triggered by writing 1 to SAPHASQTRIG ASQTRIG 19 4 2 Stop Measurement Before Completion While the USS module is performing a measurement the PSQ can stop the current measurement process using any of these methods Write 1 to UUPSCTL USSSTOP The PSQ asserts the PSQ_STOP signal to the ASQ then the ASQ sta...

Страница 465: ...mum of four different sources see the device specific data sheet for implementation When UUPSCTL USSPWRUPSEL 0 UUPSCTL USSPWRUP is selected In the case writing 1 to UUPSCTL USSPWRUP asserts the USS_PWRREQ signal to the PSQ then the PSQ starts the power up sequences and then the PSQ can trigger the PSQ to perform new measurements if UUPSCTL ASQEN 1 and SAPHASCTL0 TRIGSEL 1 Writing 1 to UUPSCTL USSP...

Страница 466: ... takes more time than expected The USS module is powered off and the UUPSRIS PTMOUT is set to 1 PREQIG interrupt This interrupt is reported when a new USS_PWRREQ is detected before completing the previous measurement Two conditions of the USS_PWRREQ signal cannot be detected 1 After detecting a valid USS_PWRREQ signal another USS_PWRREQ is applied within 3 MODOSC clock cycles 2 After UUPSRIS PREQI...

Страница 467: ... Acronym Register Name Type Reset Section 0h UUPSIIDX Interrupt Index Register read only 0 Section 19 7 1 2h UUPSMIS Masked Interrupt Status Register read only 0h Section 19 7 2 4h UUPSRIS Raw Interrupt Status Register read only 0h Section 19 7 3 6h UUPSIMSC Interrupt Mask Register read write 0h Section 19 7 4 8h UUPSICR Interrupt Clear Register write only 0h Section 19 7 5 Ah UUPSISR Interrupt Fl...

Страница 468: ...es a value that can be used as address offset for fast interrupt service routine handling On each read only one interrupt is indicated On a read the current interrupt highest priority is automatically cleared by the hardware and the corresponding interrupt flag in RIS and MIS are cleared as well After a read from the CPU not from the debug interface the register must be updated with the next highe...

Страница 469: ...ter 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED STPBYDB PREQIG PTMOUT R 0h R 0h R 0h R 0h Table 19 9 UUPSMIS Register Field Descriptions Bit Field Type Reset Description 15 3 RESERVED R 0h Reserved 2 STPBYDB R 0h USS has been interrupted by debug mode Masked Interrupt Status bit Reset type PUC 0h R No interrupt pending 1h R Interrupt pending 1 PREQIG R 0h UUPS Power Request Ignore...

Страница 470: ...PSTATE 3 The interrupt indicates that any existing activity of USS will be or has been stopped due to entering debug halt If USS_BUSY 1 and STPBYDB 1 then USS is in the middle of stopping the exisitng activities If USS_BUSY 0 and STPBYDB 1 then USS is in idle state Reset type PUC 0h R USS has not been interrupted by debug halt mode 1h R USS has been interrupted by debug halt mode 1 PREQIG R 0h Pow...

Страница 471: ...mask Figure 19 8 UUPSIMSC Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED STPBYDB PREQIG PTMOUT R 0h R W 0h R W 0h R W 0h Table 19 11 UUPSIMSC Register Field Descriptions Bit Field Type Reset Description 15 3 RESERVED R 0h Reserved 2 STPBYDB R W 0h USS has been interrupted by debug mode Interrupt Mask bit Reset type PUC 0h R STPBYDB Interrupt is disabled 1h R STPBYDB Interrup...

Страница 472: ...lear the corresponding RIS bit Read as zero Figure 19 9 UUPSICR Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED STPBYDB PREQIG PTMOUT R 0h W 0h W 0h W 0h Table 19 12 UUPSICR Register Field Descriptions Bit Field Type Reset Description 15 3 RESERVED R 0h Reserved 2 STPBYDB W 0h USS has been interrupted by debug mode Interrupt Clear bit Reset type PUC 1 PREQIG W 0h Power Reques...

Страница 473: ...Register Read as zero Figure 19 10 UUPSISR Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED STPBYDB PREQIG PTMOUT R 0h W 0h W 0h W 0h Table 19 13 UUPSISR Register Field Descriptions Bit Field Type Reset Description 15 3 RESERVED R 0h Reserved 2 STPBYDB W 0h USS has been interrupted by debug mode Interrupt Set bit Reset type PUC 1 PREQIG W 0h Power Request Ignored Interrupt Set...

Страница 474: ...UUPS Descriptor Register L Figure 19 11 UUPSDESCLO Register 15 14 13 12 11 10 9 8 FEATUREVER INSTNUM R 0h R 1h 7 6 5 4 3 2 1 0 MAJREV MINREV R 1h R 0h Table 19 14 UUPSDESCLO Register Field Descriptions Bit Field Type Reset Description 15 12 FEATUREVER R 0h Feature Set for the module Reset type PUC 11 8 INSTNUM R 1h Instance Number within the device This will be a parameter to the RTL for modules t...

Страница 475: ...7 8 UUPSDESCHI Register Offset Eh reset BA10h UUPSDESCHI is shown in Figure 19 12 and described in Table 19 15 Return to Summary Table UUPS Descriptor Register H Figure 19 12 UUPSDESCHI Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 MODULEID R BA10h Table 19 15 UUPSDESCHI Register Field Descriptions Bit Field Type Reset Description 15 0 MODULEID R BA10h Module Identifier Reset type PUC ...

Страница 476: ...ed when the powerdown request has been completed Note that if this bit is set to 1 when the USS module is in OFF state it is cleared immediately Reset type PUC 0h R W No action 1h R W Stop the current measurement and power off the USS module 13 12 LBHDEL R W 0h Low power bias hold off delay These bits define the duration of the hold off delay for the low power bias mode SAPHMCNF LPBE 1 The hold of...

Страница 477: ...et state 6 4 RESERVED R 0h Reserved 3 USS_BUSY R 0h USS Busy bit Read Only This bit is set to 1 if one of the following conditions is met 1 CTL UPSTATE 2 2 ASQ is in the middl of performing a measurement process 3 SDHS CTL5 SDHS_LOCK 1 Reset type PUC 0h R The USS module is not busy 1h R The USS module is busy 2 1 UPSTATE R 0h USS Power state bits Read Only Note Due to the synchronization issue wit...

Страница 478: ...HSPLL Chapter 20 SLAU367P October 2012 Revised April 2020 High Speed PLL HSPLL This chapter describes the operation of the HSPLL module Topic Page 20 1 Introduction 479 20 2 OSC Control Register HSPLLUSSXTCTL 480 20 3 PLL Control CTL Register 481 20 4 Start up Sequence of the USSXT Oscillator 481 20 5 Interrupts 482 20 6 HSPLL Registers 483 ...

Страница 479: ...PLL is one of the submodules in the Ultrasonic Sensing Solution USS module The USS module is designed for analog to digital converter ADC based ultrasonic sensing technology in various measurement applications Figure 20 1 shows the block diagram of the USS module Figure 20 1 USS or USS_A Block Diagram The HSPLL module is the dedicated clock generation module for the USS module To measure the flow ...

Страница 480: ...ting 1 to HSPLLUSSXTCTL OSCEN Ceramic resonators have faster wake up time than crystal resonators For a crystal resonator TI recommends setting HSPLLUSSXTCTL OSCTYPE to 0 gating counter 4096 For a ceramic resonator TI recommends setting HSPLLUSSXTCTL OSCTYPE to 1 gating counter 512 20 2 3 OSCSTATE Bit The HSPLLUSSXTLCTL OSCSTATE bit is set after the predefined cycle count has been reached after th...

Страница 481: ...OCK bit indicates whether or not the PLL output clock is stable HSPLLCTL PLL_LOCK is set to 1 when the PLL output frequency reaches the desired frequency and becomes stable The lock signal is also used by the PSQ during its power up sequence When the PLL output is changed from locked to unlocked the PLL unlock interrupt bit HSPLLRIS PLLUNLOCK is set When the PLL unlock interrupt occurs TI recommen...

Страница 482: ...pacitance and inductance of the PCB traces and package as tank circuits and tend to oscillate on its harmonic frequencies during power up Increasing the value of the serial resistance between USSXTOUT and crystal or resonator prevents such oscillation conditions at those higher frequencies The maximum time for crystals and resonators is give in the data sheet USSXT_BOUT can be used to monitor USSX...

Страница 483: ... Interrupt Index Register read only 0 Section 20 6 1 2h HSPLLMIS Masked Interrupt Status Register read only 0h Section 20 6 2 4h HSPLLRIS Raw Interrupt Status Register read only 0h Section 20 6 3 6h HSPLLIMSC Interrupt Mask Register read write 0h Section 20 6 4 8h HSPLLICR Interrupt Flag Clear Register write only 0h Section 20 6 5 Ah HSPLLISR Interrupt Flag Set Register write only 0h Section 20 6 ...

Страница 484: ...lue Read only It generates a value that can be used as address offset for fast interrupt service routine handling On each read only one interrupt is indicated On a read the current interrupt highest priority is automatically cleared by the hardware and the corresponding interrupt flag in RIS and MISC are cleared as well After a read from the CPU not from the debug interface the register must be up...

Страница 485: ... Figure 20 4 and described in Table 20 3 Return to Summary Table Masked Interrupt Status Register Figure 20 4 HSPLLMIS Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED PLLUNLOCK R 0h R 0h Table 20 3 HSPLLMIS Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved 0 PLLUNLOCK R 0h HSPLL Unlock Masked Interrupt Status bit Reset type PUC 0h R No i...

Страница 486: ...terrupt as the interrupt does not need to be enabled Note that the HSPLLRIS flag can be cleared by writing to the MISC register bit even if the corresponding IM bit is not enabled Figure 20 5 HSPLLRIS Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED PLLUNLOCK R 0h R 0h Table 20 4 HSPLLRIS Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved ...

Страница 487: ...ble 20 5 Return to Summary Table Interrupt Mask Register Note writing 1 enables the corresponding interrupt Figure 20 6 HSPLLIMSC Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED PLLUNLOCK R 0h R W 0h Table 20 5 HSPLLIMSC Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved 0 PLLUNLOCK R W 0h PLL Unlock Interrupt Mask bit Reset type PUC 0h R...

Страница 488: ...hown in Figure 20 7 and described in Table 20 6 Return to Summary Table Interrupt Flag Clear Register Read as zero Figure 20 7 HSPLLICR Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED PLLUNLOCK R 0h W 0h Table 20 6 HSPLLICR Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved 0 PLLUNLOCK W 0h PLL Unlock Interrupt Clear bit Write 1 to clear ...

Страница 489: ...s shown in Figure 20 8 and described in Table 20 7 Return to Summary Table Interrupt Flag Set Register Read as zero Figure 20 8 HSPLLISR Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED PLLUNLOCK R 0h W 0h Table 20 7 HSPLLISR Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved 0 PLLUNLOCK W 0h PLL Unlock Interrupt Set bit Write 1 to set RIS...

Страница 490: ...Descriptor Register L Figure 20 9 HSPLLDESCLO Register 15 14 13 12 11 10 9 8 FEATUREVER INSTNUM R 0h R 1h 7 6 5 4 3 2 1 0 MAJREV MINREV R 1h R 0h Table 20 8 HSPLLDESCLO Register Field Descriptions Bit Field Type Reset Description 15 12 FEATUREVER R 0h Feature Set for the module Reset type PUC 11 8 INSTNUM R 1h Instance Number within the device This will be a parameter to the RTL for modules that c...

Страница 491: ...PLLDESCHI Register Offset Eh reset BD10h HSPLLDESCHI is shown in Figure 20 10 and described in Table 20 9 Return to Summary Table HSPLL Descriptor Register H Figure 20 10 HSPLLDESCHI Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 MODULEID R BD10h Table 20 9 HSPLLDESCHI Register Field Descriptions Bit Field Type Reset Description 15 0 MODULEID R BD10h Module Identifier Reset type PUC ...

Страница 492: ...e 16 Valid data range 16 39 The input clock to the PLL block must be 4MHz 8MHz Care needs to be taken to choose PLLM 5 0 value that the final output clock must be in range of 68MHz 80MHz Note that PLLM 5 0 needs to be configured with the desired value before powering up the USS module and must not be changed while the USS module is on 10h R W 16 11h R W 17 12h R W 18 13h R W 19 14h R W 20 15h R W ...

Страница 493: ...ble 20 10 HSPLLCTL Register Field Descriptions continued Bit Field Type Reset Description 0 PLL_LOCK R 0h PLL Lock Status Note When PLL output is changed from locked status to unlock status PLL Unlock Interrupt bit RIS PLLUNLOCK is set It is recommned to enable the interrupt while performing a measurement Reset type PUC 0h R PLL is not running or not locked 1h R PLL is locked ...

Страница 494: ...lock frequency to HSPLL 0h R XTAL Gating Counter Length 4096 It is recommended to use this configuration for crystal resonators Note the counter counts the oscillator clock so total time can be calculated as Time 4096 x 1 Oscillator Clock Frequency 1h R CERAMIC Gating Counter Length 512 It is recommended to use this configuration for ceramic resonators Note the counter counts the oscillator clock ...

Страница 495: ... Revised April 2020 Sequencer for Acquisition Programmable Pulse Generator and Physical Interface SAPH SAPH_A This chapter describes the operation of the SAPH module Topic Page 21 1 Introduction 496 21 2 Programmable Pulse Generator PPG or PPG_A Block 497 21 3 Physical Interface PHY Block 504 21 4 Acquisition Sequencer ASQ 510 21 5 Ultra Low Power Bias Mode 514 21 6 Interrupts Triggers 515 21 7 DM...

Страница 496: ...Y SAPH_A provides additional bias voltages for optional external signal conditioning like low noise amplifiers LNAs and booster amplifiers PPG or PPG_A block Generates pulses at different frequencies PHY block Controls output channels and input channels of the USS module ASQ block The entire measurement sequence can be controlled by user software called register mode or by ASQ without any CPU inte...

Страница 497: ... controlled Optional external signal handling Vout OSC PLL USSXTIN USSXTOUT USSXT_BOUT USSXT HSPLL SAPH or SAPH_A SDHS DTC RAM shared with LEA USS or USS_A module PLL_CLK Px y XPB0 XPB1 www ti com Programmable Pulse Generator PPG or PPG_A Block 497 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sequencer for Acquisition Pro...

Страница 498: ...ompared to the excitation pulses The PPG generates up to 127 excitation pulses and up to 15 stop pulses which are controlled by the SAPHPGC EPULS and SAPHPGC SPULS bits respectively The pulse polarity is programmable in the SAPHPGC PPOL bit The signal polarity for Pause can be programmed to be logical high logical low or high impedance through the SAPHPGC PLEV and SAPHPGC PHIZ bits The PPG can be ...

Страница 499: ... The stop pulses have same frequency as the regular excitation pulses The PPG generates up to 127 extra excitation pulses up to 127 regular excitation pulses and up to 15 stop pulses which are controlled by the SAPH_AXPGCTL XPULS SAPH_APGC EPULS and SAPH_APGC SPULS bits respectively The pulse polarity is programmable in the SAPH_APGC PPOL bit The signal polarity of Pause can be programmed to be lo...

Страница 500: ...terminate the trill The last regular excitation pulses are followed by stop pulses Then PPG_A goes to Pause phase again see Figure 21 8 and Figure 21 9 The stop pulses have a 180 phase shift compared to the last regular excitation pulses The stop pulses have same frequency as the last regular excitation pulses The PPG generates up to 127 extra excitation pulses up to 127 regular excitation pulses ...

Страница 501: ...efined set of Extra_Excitation and Regular_Excitation phases Stop and Pause again A state machine in PPG_A controls the flow Set SAPH_AXPGCTL XMOD 3 like for trill tone generation When the PPG_A is triggered it leaves the Pause phase generates extra excitation pulses with a frequency defined by SAPH_AXPGHPER SAPH_AXPGLPER then regular excitation pulses with a frequency defined by SAPH_APGHPER SAPH...

Страница 502: ...ts keep SAPH_APGCTL PPGEN 0 while preparing the PPG_A registers After the PPG_A registers are prepared write 1 to the SAPH_APGCTL PPGEN bit before triggering the PPG_A The SAPH_APGCTL PPGEN bit must be set before triggering the PPG_A The output channel is determined by the SAPH_APGCTL PPGCHSEL bit when SAPH_APGCTL PGSEL 0 register mode or by the acquisition sequencer ASQ when SAPH_APGCTL PGSEL 1 a...

Страница 503: ...hus Excitation pulse frequency HSPLL frequency SAPHPGHPER HPER SAPHPGLPER LPER 21 2 7 Extra Excitation Pulse Frequency on PPG_A The pulse frequency for the X Pulses is determined by the PPG_A clock frequency and the SAPH_AXPGLPER XLPER and SAPH_AXPGHPER XHPER bits The high duration of an extra excitation pulse and low duration of an extra excitation pulse are determined by SAPH_AXPGHPER XHPER 8 bi...

Страница 504: ... the input and output pins of the USS module The USS module has dedicated pins CH0_OUT CH0_IN CH1_OUT CH1_IN two PVSS and PVCC which are controlled by the USS module not by the digital I O module 21 3 1 Output Channels CH0_OUT and CH1_OUT Figure 21 12 shows the functional block diagram for the output channels CH0_OUT and CH1_OUT Figure 21 12 PHY Output Pins The output pins CH0_OUT and CH1_OUT can ...

Страница 505: ...onsists of PMOS and NMOS Thus three trim registers are offered for each channel see Table 21 1 for details During manufacturing optimal impedance of the drivers and termination switches are determined and their trim values are stored to the device boot data memory not user accessible The output impedance of DRV0 and DRV1 are trimmed to match each other with the lowest possible value and the termin...

Страница 506: ... LPBE 0 auto mode Register mode uses the SAPHOCTL0 SAPHOCTL1 SAPHOSEL and SAPHBCTL regiters to control the signal chain Auto mode uses the SAPHASCTL0 SAPHASCTL1 SAPHAPOL SAPHAPLEV and SAPHAHIZ registers to control the signal chain In Ultra Low Power Bias mode SAPHMCNF 1 both register sets are and the multiplexer selection is controlled by the ASQ The PGA has two input channels but one of the chann...

Страница 507: ...TL CPDA 0 default The charge pump is automatically off when data capture begins 300 µs SAPHBCTL CPDA 1 The charge pump remains on during data capture 300 µs 21 3 3 1 Tx Bias and Rx Bias During a measurement sequence bias voltages must be applied appropriately to the transmit signal and receive signal In auto mode the entire measurement sequence including applying appropriate bias voltages is fully...

Страница 508: ...entric signal PVcc 4 Bias centric Dummy Input SAPHMCNF CPEO Physical Interface PHY Block www ti com 508 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sequencer for Acquisition Programmable Pulse Generator and Physical Interface SAPH SAPH_A NOTE Excitation pulses are driven on CH0_OUT and CH0_IN is connected to the PGA dumm...

Страница 509: ... 1 1 from ASQ SAPHMCNF LPBE SAPHMCNF CPEO SAPHMCNF BIMP Rx Bias SAPHMCNF BIMP Ground centric signal TxBias centric signal RxBias centric signal PVcc 4 centric signal PVcc 2 centric signal PVcc 4 Bias centric Dummy Input www ti com Physical Interface PHY Block 509 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sequencer for ...

Страница 510: ...independently by SAPHBCTL EXCBIAS and SAPHBCTL PGABIAS respectively 21 3 4 External Bias XPB0 and XPB1 on SAPH_A The SAPH_A module features external bias terminals XPB0 and XPB1 Set SAPH_AICTL0 XPB0FEN 1 to enable the analog bias function on the XPB0 terminal Use SAPH_AICTL0 XPBSW0 to turn the bias switch on or off If SAPH_AICTL0 XPB0FEN 0 the terminal is used as a regular digital port pin On SAPH...

Страница 511: ...Timemark E Timemark F www ti com Acquisition Sequencer ASQ 511 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sequencer for Acquisition Programmable Pulse Generator and Physical Interface SAPH SAPH_A Figure 21 18 ASQ Block Diagram 21 4 1 Time Counter Figure 21 17 shows that the ASQ has a 20 bit time counter running at 1 16 ...

Страница 512: ...time mark events is determined by the counter values written to the SAPHATM_x registers Time mark event period PLL clock 1 16 value in the time mark registers for TMA TMB TMC and TMD TME event period PLL clock 1 16 value in the time mark register 16 TMF event period PLL clock 1 16 value in the time mark register 4 21 4 3 Triggering the ASQ There are two ways to start the ASQ One is user software t...

Страница 513: ... TxBias and RxBias impdance SAPHMCNF BIMP 0 1 2 3 SAPHMCNF BIMP SAPHMCNF BIMP 0 1 2 3 SAPHMCNF BIMP Drive output drivers to GND SAPHOSEL PCH0SEL 1 N A automatic SAPHOSEL PCH0SEL 0 SAPHOCTL0 CH0TERM SAPHOCTL0 CH1TERM Tx bias SAPHBCTL ASQBSW 1 N A automatic SAPHBCTL ASQBSW 0 SAPHBCTL CH0EBSW SAPHBCTL CH1EBSW Select output channel in PPG SAPHPGCTL PGSEL 1 SAPHASCTL0 ASQCHSEL SAPHASCTL1 CHTOG SAPHPGCT...

Страница 514: ...ircuits may show ringing due to power up and bias voltage enable The signals settle then At d the HSPLL generates a clock with almost no remaining phase variations Near TA the transducers have settled and the regular sequence is started by generating pulses At TB well before the arrival of the signal the SDHS and its clock is enabled At TD the data acquisition starts At e the sequence is completed...

Страница 515: ...odule supports four interrupts PNGDN interrupt The interrupt occurs when the PPG completes pulse generation SEQDN interrupt The interrupt occurs when ASQ completes all of the measurements programmed in SAPHASCTL0 PNGCNT For example when SAPHASCTL0 PNGCNT 3 four measurements are performed The interrupt indicates that all four measurements have been completed NOTE After ASQ is triggered if the curre...

Страница 516: ... write only 0h Section 21 8 9 12h SAPHOCTL0 SAPH_AOCTL0 Physical Interface Output Control 0 read write 0h Section 21 8 10 14h SAPHOCTL1 SAPH_AOCTL1 Physical Interface Output Control 1 read write 0h Section 21 8 11 16h SAPHOSEL SAPH_AOSEL Physical Interface Output Function Select read write 5h Section 21 8 12 20h SAPHCH0PUT SAPH_ACH0PUT Channel 0 Pull UpTrim Register read write 0h Section 21 8 13 2...

Страница 517: ...read write 0h Section 21 8 32 64h SAPHASQTRIG APH_AASQTRIG ASQ Software Trigger write only 0h Section 21 8 33 66h SAPHAPOL SAPH_AAPOL ASQ ping output polarity read write 0h Section 21 8 34 68h SAPHAPLEV SAPH_AAPLEV ASQ ping pause level read write 0h Section 21 8 35 6Ah SAPHAPHIZ SAPH_AAPHIZ ASQ ping pause impedance read write 0h Section 21 8 36 6Eh SAPHATM_A SAPH_AATM_A A SEQ start to 1st ping rea...

Страница 518: ...abled interrupt index Reset type PUC 0h R W NONE no interrupts pending 1h R W DATAERR This interrupt indicates that either WINHI interrupt or WINLO interrupt has occurred in SDHS 2h R W TMFTO This interrupt is valid when ASQ is activcve auto mode The interrupt indicates that the time counter in ASQ has reached to TIMEMARK_F timeout 3h R W SEQDN This interrupt is valid when ASQ is activcve auto mod...

Страница 519: ...set Description 15 4 RESERVED R 0h 3 PNGDN RH 0h This interrupt is valid when ASQ is active auto mode The interrupt occurs when ASQ completes one measurement sequence For example when SAPHASCTL0 PNGCNT 3 total four measurements are performed The interrupt indicates that one measurement has been completed Reset type PUC 2 SEQDN RH 0h This interrupt is valid when ASQ is activcve auto mode The interr...

Страница 520: ...14 DAV RH 0h This bit indicates a DMA access violation Reset type PUC 13 4 RESERVED R 0h 3 PNGDN RH 0h This interrupt is valid when ASQ is active auto mode The interrupt occurs when ASQ completes one measurement sequence For example when SAPHASCTL0 PNGCNT 3 total four measurements are performed The interrupt indicates that one measurement has been completed Reset type PUC 2 SEQDN RH 0h This interr...

Страница 521: ... 21 24 SAPHIMSC SAPH_AIMSC Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED DAV PNGDN SEQDN TMFTO DATAERR R W 0h RH 0h R W 0h R W 0h R W 0h R W 0h Table 21 9 SAPHIMSC SAPH_AIMSC Register Field Descriptions Bit Field Type Reset Description 15 5 RESERVED R W 0h 4 DAV RH 0h This bit indicates a DMA access violation Reset type PUC 3 PNGDN R W 0h This bit enables the PNGDN interr...

Страница 522: ... DAV RESERVED W 0h HW1C 0h W 0h 7 6 5 4 3 2 1 0 RESERVED PNGDN SEQDN TMFTO DATAERR W 0h HW1C 0h HW1C 0h HW1C 0h HW1C 0h Table 21 10 SAPHICR SAPH_AICR Register Field Descriptions Bit Field Type Reset Description 15 RESERVED W 0h 14 DAV HW1C 0h Writing one this bit to clear any previous DMA access violations 13 4 RESERVED W 0h 3 PNGDN HW1C 0h Writing one this bit to clear the pending PNGDN interrupt...

Страница 523: ...RVED W 0h HW1S 0h W 0h 7 6 5 4 3 2 1 0 RESERVED PNGDN SEQDN TMFTO DATAERR W 0h HW1S 0h HW1S 0h HW1S 0h HW1S 0h Table 21 11 SAPHISR SAPH_AISR Register Field Descriptions Bit Field Type Reset Description 15 RESERVED W 0h 14 DAV HW1S 0h Writing one this bit to set RIS DAV by software Reset type PUC 13 4 RESERVED W 0h 3 PNGDN HW1S 0h Writing one this bit to generate a PNGDN interrupt by software Reset...

Страница 524: ...eset 10h SAPHDESCLO SAPH_ADESCLO is shown in Figure 21 27 and described in Table 21 12 Return to Summary Table Module Descriptor Low Word Figure 21 27 SAPHDESCLO SAPH_ADESCLO Register 15 14 13 12 11 10 9 8 FEATUREVER INSTNUM R 0h R 0h 7 6 5 4 3 2 1 0 MAJREV MINREV R 1h R 0h Table 21 12 SAPHDESCLO SAPH_ADESCLO Register Field Descriptions Bit Field Type Reset Description 15 12 FEATUREVER R 0h Featur...

Страница 525: ... SAPH SAPH_A 21 8 8 SAPHDESCHI SAPH_ADESCHI Register Offset Eh reset 5553h SAPHDESCHI SAPH_ADESCHI is shown in Figure 21 28 and described in Table 21 13 Return to Summary Table Module Descriptor High Word Figure 21 28 SAPHDESCHI SAPH_ADESCHI Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 ModuleID R 5553h Table 21 13 SAPHDESCHI SAPH_ADESCHI Register Field Descriptions Bit Field Type Reset Descripti...

Страница 526: ...H_AKEY Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 KEY W 0h Table 21 14 SAPHKEY SAPH_AKEY Register Field Descriptions Bit Field Type Reset Description 15 0 KEY W 0h This field must be written with 0x454B using a word write to unlock the SAPH registers for write accesses Writing a value other than 0x454B locks the SAPH registers again The KEY register only locks unlocks the SAPH registers with o...

Страница 527: ...0 RESERVED R W 0h 9 CH1OUT R W 0h CH1_OUT Value When SAPHOSEL PCH1SEL 0 and SAPHOCTL0 CH1OE 1 this bit represents the logical value on the CH1 terminal 0 low 1 high Reset type PUC 0h R W Ch1 is set to low signal 1h R W Ch1 is set to high signal 8 CH0OUT R W 0h CH0_OUT Value When SAPHOSEL PCH0SEL 0 and SAPHOCTL0 CH0OE 1 this bit represents the logical value on the CH0 terminal 0 low 1 high Reset ty...

Страница 528: ...1 Output is set to normal strength 1h R W Ch1 Output is set to maximum strength 8 CH0FP R W 0h DRV0 output driver on the CH0_OUT full strength enable 0 The DRV0 output impedance is deterimed by SAPHCH0PUT and SAPHCH0PDT registers 1 The DRV0 has lowest output impedance Reset type PUC 0h R W Ch0 Output is set to normal strength 1h R W Ch0 Output is set to maximum strength 7 2 RESERVED R W 0h 1 CH1TE...

Страница 529: ...on 15 4 RESERVED R W 0h 3 2 PCH1SEL R W 1h Output functional select for CH0_OUT Reset type PUC 0h R W GPIO CH1_OUT is used as a GPO pin It is controlled by SAPHOCTL0 CH1OUT and SAPHOCTL0 CH1OE 1h R W PPGSE CH1_OUT is driven by the PPG 2h R W CH1_OUT is driven by the PPG as differential output along with CH0_OUT CH0_OUT and CH1_OUT are always opposite polarity 3h R W CH1_OUT is used as a GPO pin It...

Страница 530: ...1 33 and described in Table 21 18 Return to Summary Table DRV0 CH0_OUT driver Trim Register for pull up Figure 21 33 SAPHCH0PUT SAPH_ACH0PUT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH0PUT R W 0h R W 0h Table 21 18 SAPHCH0PUT SAPH_ACH0PUT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH0PUT R W 0h DRV0 pull up trim register Wri...

Страница 531: ...34 and described in Table 21 19 Return to Summary Table DRV0 CH0_OUT driver Trim Register for pull down Figure 21 34 SAPHCH0PDT SAPH_ACH0PDT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH0PDT R W 0h R W 0h Table 21 19 SAPHCH0PDT SAPH_ACH0PDT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH0PDT R W 0h DRV0 pull down trim register W...

Страница 532: ...ure 21 35 and described in Table 21 20 Return to Summary Table SWG0 CH0_OUT termination switch Trim Register Figure 21 35 SAPHCH0TT SAPH_ACH0TT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH0TT R W 0h R W 0h Table 21 20 SAPHCH0TT SAPH_ACH0TT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH0TT R W 0h SWG0 trim register Write access...

Страница 533: ...1 36 and described in Table 21 21 Return to Summary Table DRV1 CH1_OUT driver Trim Register for pull up Figure 21 36 SAPHCH1PUT SAPH_ACH1PUT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH1PUT R W 0h R W 0h Table 21 21 SAPHCH1PUT SAPH_ACH1PUT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH1PUT R W 0h DRV1 pull up trim register Wri...

Страница 534: ...37 and described in Table 21 22 Return to Summary Table DRV1 CH1_OUT driver Trim Register for pull down Figure 21 37 SAPHCH1PDT SAPH_ACH1PDT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH1PDT R W 0h R W 0h Table 21 22 SAPHCH1PDT SAPH_ACH1PDT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH1PDT R W 0h DRV1 pull down trim register W...

Страница 535: ...gure 21 38 and described in Table 21 23 Return to Summary Table SWG1 CH1_OUT termination switch Trim Register Figure 21 38 SAPHCH1TT SAPH_ACH1TT Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED CH1TT R W 0h R W 0h Table 21 23 SAPHCH1TT SAPH_ACH1TT Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 CH1TT R W 0h SWG1 trim register Write acces...

Страница 536: ... R W For manual bias mode and regular ASQ bias mode In this configuration the user controls by the ASQBSW has full control over the TxBias and RxBias switches 1h R W Low power bias mode In this mode the ASQ uses the CHxEBSW and PGABSW as auxiliary values to achieve faster channel setting on reactive input loads The ASQ has full controls over the bias switch multiplexer 10 9 RSV1 R W 0h Reserved fo...

Страница 537: ...n in Figure 21 40 and described in Table 21 25 Return to Summary Table Trim Access Control Register Figure 21 40 SAPHTACTL SAPH_ATACTL Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED RESERVED UNLOCK R W 0h R 0h R W 0h Table 21 25 SAPHTACTL SAPH_ATACTL Register Field Descriptions Bit Field Type Reset Description 15 3 RESERVED R W 0h 2 1 RESERVED R 0h Reserved 0 UNLOCK R W 0h...

Страница 538: ... 1 control only on SAPH_A Reset type PUC 0h R W External bias switch is open no bias driven 1h R W External bias switch is closed bias is driven 12 XPBSW0 R W 0h External PGA Bias Switch 0 control only on SAPH_A Reset type PUC 0h R W External bias switch is open no bias driven 1h R W External bias switch is closed bias is driven 11 10 RESERVED R W 0h 9 XPB1FEN R W 0h XPB1 Pin Function Enable only ...

Страница 539: ...ltiplexer Channel Select Reset type PUC 0h R W CH0IN Channel 0 is selected for input 1h R W CH1IN Channel 1 is selected for input 2h R W reserved for future channels 3h R W reserved for future channels 4h R W reserved for future channels 5h R W reserved for future channels 6h R W reserved for future channels 7h R W reserved for future channels 8h R W no channel is selected 9h R W no channel is sel...

Страница 540: ... Tx bias switch to CH1 is closed enabled 8 CH0EBSW R W 0h Channel 0 Tx bias Switch Control Note that the Tx bias voltage is determined by SAPHBCTL EXCBIAS Reset type PUC 0h R W Tx bias switch to CH0 is open 1h R W Tx bias switch to CH0 is closed enabled 7 6 PGABIAS R W 2h PGA bias Rx bias Voltage Select Reset type PUC 0h R W 0 75V nominal 1h R W 0 8V nominal 2h R W 0 9V nominal 3h R W 0 95V nomina...

Страница 541: ...ble Pulse Generator and Physical Interface SAPH SAPH_A Table 21 27 SAPHBCTL SAPH_ABCTL Register Field Descriptions continued Bit Field Type Reset Description 0 ASQBSC R W 1h Tx bias and Rx bias switches control source select Reset type PUC 0h R W Bias switches are controlled by SAPHBCTL CH0EBSW SAPHBCTL CH1EBSW SAPHBCTL PGABSW bits register mode 1h R W Bias switches are controlled by ASQ auto mode...

Страница 542: ... by SAPHPGC PLEV bit 1h R W PPG output is in Hi Z during inactive regardless of SAPHPGC PLEV bit 14 PLEV R W 0h PPG ouptut level during inactive This bit affects the status of PPG output before and after excitations Note that this bit is only valid when SAPHPGC PHIZ 0 Reset type PUC 0h R W PPG output is low during inactive 1h R W PPG output is high during inactive 13 PPOL R W 0h Pulse Polarity Thi...

Страница 543: ...is shown in Figure 21 44 and described in Table 21 29 Return to Summary Table PPG output pulse low period Figure 21 44 SAPHPGLPER SAPH_APGLPER Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 LPER R W 0h Table 21 29 SAPHPGLPER SAPH_APGLPER Register Field Descriptions Bit Field Type Reset Description 15 8 RESERVED R W 0h 7 0 LPER R W 0h Low phase period of PPG excitation pulses This v...

Страница 544: ...s shown in Figure 21 45 and described in Table 21 30 Return to Summary Table PPG output pulse high period Figure 21 45 SAPHPGHPER SAPH_APGHPER Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 HPER R W 0h Table 21 30 SAPHPGHPER SAPH_APGHPER Register Field Descriptions Bit Field Type Reset Description 15 8 RESERVED R W 0h 7 0 HPER R W 0h High phase period of PPG excitation pulses This ...

Страница 545: ...rsists while SAPHPGCTL TONE 1 SAPHPGCTL STOP 0 Either writing 0 to SAPHPGCTL TONE or writing 1 to SAPHPGCTL STOP stops tone generation Reset type PUC 0h R W ENABLE Test tone generation is enabled 13 PSCEN R W 0h Test feature Keep this bit zero for proper operation Reset type PUC 0h R W disabled 1h R W enabled PPG is clocked with 1 4 of PLL_CLK without phase control 12 RESERVED R W 0h 11 10 RESERVE...

Страница 546: ... Acquisition Programmable Pulse Generator and Physical Interface SAPH SAPH_A Table 21 31 SAPHPGCTL SAPH_APGCTL Register Field Descriptions continued Bit Field Type Reset Description 0 PGSEL R W 1h PPG output channel select source Reset type PUC 0h R W PPG output channel is selected by SAPHPGCTL PPGCHSEL bit register mode 1h R W PPG output channel is selected by ASQ auto mode ...

Страница 547: ...IG SAPH_APPGTRIG is shown in Figure 21 47 and described in Table 21 32 Return to Summary Table PPG Software Trigger Register Figure 21 47 SAPHPPGTRIG SAPH_APPGTRIG Register 15 14 13 12 11 10 9 8 RESERVED W 0h 7 6 5 4 3 2 1 0 RESERVED PPGTRIG W 0h W 0h Table 21 32 SAPHPPGTRIG SAPH_APPGTRIG Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED W 0h 0 PPGTRIG W 0h Writing 1 to th...

Страница 548: ...TY R W 0h Event type Selects the type of the event generated in SAPH_AXPGCTL XMOD 3 Reset type PUC 0h R W Timer count event 1h R W DMA trigger event 13 12 XMOD R W 0h Extended Mode Select Reset type PUC 0h R W Single tone generation Pause E S Pause 1h R W reserved 2h R W Dual Tone Generation Pause X E S Pause 3h R W Dual Tone Loop X E X E triggers events 11 10 RESERVED R W 0h 9 8 XSTAT RH 0h Phase...

Страница 549: ... 49 and described in Table 21 34 Return to Summary Table Extra Pulse Low Period Register Figure 21 49 SAPH_AXPGLPER Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 XLPER R W 0h Table 21 34 SAPH_AXPGLPER Register Field Descriptions Bit Field Type Reset Description 15 8 RESERVED R W 0h 7 0 XLPER R W 0h XLPER low phase period of the extra pulses This value defines the length of the low...

Страница 550: ...1 50 and described in Table 21 35 Return to Summary Table Extra Pulse High Period Register Figure 21 50 SAPH_AXPGHPER Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 XHPER R W 0h Table 21 35 SAPH_AXPGHPER Register Field Descriptions Bit Field Type Reset Description 15 8 RESERVED R W 0h 7 0 XHPER R W 0h XHPER high phase period of the extra pulses This value defines the length of the ...

Страница 551: ...e Note that it is not possible to resume the measurement from where it was stopped When ASQ is triggered again the measurement seqeunce starts from the beginning Reset type PUC 0h R W Continue the measurements until completion regardless of the DATAERR interrupt 1h R W Stop the ASQ upon the DATAERR interrupt 12 RESERVED R 0h Reserved 11 10 TRIGSEL R W 0h ASQ trigger select Reset type PUC 0h R W SW...

Страница 552: ...d SAPHASCTL1 CHTOG 1 then the channel selection would be CH0 CH1 CH0 CH1 If SAPHASCTL0 PNGCNT 3 and SAPHASCTL1 CHTOG 0 then the channel selection would be CH0 CH0 CH0 CH0 1h R W CH1 is selected to start with If SAPHASCTL0 PNGCNT 3 and SAPHASCTL1 CHTOG 0 then the channel selection would be CH1 CH1 CH1 CH1 If SAPHASCTL0 PNGCNT 3 and SAPHASCTL1 CHTOG 1 then the channel selection would be CH1 CH0 CH1 ...

Страница 553: ... Rx channel are not the same This is the typical configuration 1h R W Tx channel and Rx channel are identical 10 STDBY R W 0h ASQ can send a request sigal to the PSQ Power Sequencer of the USS module when the OFF request is received See SAPHASCTL1 ESOFF and the UUPS module Reset type PUC 0h R W PWROFF The ASQ sends a power down request to the PSQ Power Sequencer when the OFF request is received 1h...

Страница 554: ... Sequencer for Acquisition Programmable Pulse Generator and Physical Interface SAPH SAPH_A Table 21 37 SAPHASCTL1 SAPH_AASCTL1 Register Field Descriptions continued Bit Field Type Reset Description 0 CHTOG R W 0h Channel toggle enable at each PNGDN interrupt Reset type PUC 0h R W Channel toggle is disabled 1h R W Channel toggle is enabled at each PNGDN interrupt ...

Страница 555: ...fset 64h reset 0h SAPHASQTRIG SAPH_AASQTRIG is shown in Figure 21 53 and described in Table 21 38 Return to Summary Table ASQ Software Trigger Register Figure 21 53 SAPHASQTRIG SAPH_AASQTRIG Register 7 6 5 4 3 2 1 0 RESERVED ASQTRIG W 0h W 0h Table 21 38 SAPHASQTRIG SAPH_AASQTRIG Register Field Descriptions Bit Field Type Reset Description 7 1 RESERVED W 0h 0 ASQTRIG W 0h Writing 1 to this bit tri...

Страница 556: ...rolling the measurement Figure 21 54 SAPHAPOL SAPH_AAPOL Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED PCPOL R W 0h R W 0h Table 21 39 SAPHAPOL SAPH_AAPOL Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 PCPOL R W 0h Bit 0 defines the PPG pulse polarity for the first measurement Bit 1 defines the PPG pulse polarity for the second measu...

Страница 557: ...urement Figure 21 55 SAPHAPLEV SAPH_AAPLEV Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED PCPLEV R W 0h R W 0h Table 21 40 SAPHAPLEV SAPH_AAPLEV Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 PCPLEV R W 0h Bit 0 defines the PPG output level at pause for the first measurement when PCPHIZ bit 0 0 Bit 1 defines the PPG output level at pa...

Страница 558: ...easurement Figure 21 56 SAPHAPHIZ SAPH_AAPHIZ Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED PCPHIZ R W 0h R W 0h Table 21 41 SAPHAPHIZ SAPH_AAPHIZ Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R W 0h 3 0 PCPHIZ R W 0h Bit 0 defines the PPG output status at pause for the first measurement Bit 1 defines the PPG output status at pause for the sec...

Страница 559: ...e Count for the TIMEMARK A Event Figure 21 57 SAPHATM_A SAPH_AATM_A Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 TIMEMARK_A R W 0h Table 21 42 SAPHATM_A SAPH_AATM_A Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_A R W 0h This value is used to generate the TIMEMARK A event by comparing with the ASQ timer counter value TIMEMARK_A value 15 0 are compared to ASQ Timer Cou...

Страница 560: ...unt for the TIMEMARK B Event Figure 21 58 SAPHATM_B SAPH_AATM_B Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 TIMEMARK_B R W 0h Table 21 43 SAPHATM_B SAPH_AATM_B Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_B R W 0h This value is used to generate the TIMEMARK B event by comparing with the ASQ timer counter value TIMEMARK_B value 15 0 are compared to ASQ Timer Counter...

Страница 561: ...IMEMARK C Event Figure 21 59 SAPHATM_C SAPH_AATM_C Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 TIMEMARK_C R W 0h Table 21 44 SAPHATM_C SAPH_AATM_C Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_C R W 0h This value is used to generate the TIMEMARK C event by comparing with the ASQ timer counter value TIMEMARK_C value 15 0 are compared to ASQ Timer Counter 15 0 TIMEMAR...

Страница 562: ...le Count for the TIMEMARK D Event Figure 21 60 SAPHATM_D SAPH_AATM_D Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 TIMEMARK_D R W 0h Table 21 45 SAPHATM_D SAPH_AATM_D Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_D R W 0h This value is used to generate the TIMEMARK D event by comparing with the ASQ timer counter value TIMEMARK_D value 15 0 are compared to ASQ Timer Co...

Страница 563: ...d in Table 21 46 Return to Summary Table Count for the TIMEMARK E Event Figure 21 61 SAPHATM_E SAPH_AATM_E Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 TIMEMARK_E R W 0h Table 21 46 SAPHATM_E SAPH_AATM_E Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_E R W 0h This value is used to generate the TIMEMARK E event by comparing with the ASQ timer counter value TIMEMARK_E v...

Страница 564: ...0 9 8 7 6 5 4 3 2 1 0 TIMEMARK_F R W 0h Table 21 47 SAPHATM_F SAPH_AATM_F Register Field Descriptions Bit Field Type Reset Description 15 0 TIMEMARK_F R W 0h This value is used to generate the TIMEMARK F event by comparing with the ASQ timer counter value TIMEMARK_F value 15 0 are compared to ASQ Timer Counter 17 2 TIMEMARK F event is to check out if the measurement is completed within this time l...

Страница 565: ...ss 13 10 RESERVED R W 0h 9 RESERVED R 0h Reserved 8 RESERVED R 0h Reserved 7 4 PSSV R W 0h ASQ pre scaler shift The value written to the PSSV bits shifts the start point of the ASQ s pre scaler Note that the value only affects the first cycle of the pre scaler 0 No shift 1 The pre scaler starts 1 clock later 2 The pre scaler starts 2 clocks later 15 The pre scaler starts 15 clocks later Reset type...

Страница 566: ...AATIMLO Register Offset 7Ch reset 0h SAPHATIMLO SAPH_AATIMLO is shown in Figure 21 64 and described in Table 21 49 Return to Summary Table ASQ Time Counter Low Part 15 0 Figure 21 64 SAPHATIMLO SAPH_AATIMLO Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 ATIMLO R 0h Table 21 49 SAPHATIMLO SAPH_AATIMLO Register Field Descriptions Bit Field Type Reset Description 15 0 ATIMLO R 0h ASQ Timer Counter lo...

Страница 567: ...Eh reset 0h SAPHATIMHI SAPH_AATIMHI is shown in Figure 21 65 and described in Table 21 50 Return to Summary Table ASQ Time Counter High Part 19 16 Figure 21 65 SAPHATIMHI SAPH_AATIMHI Register 15 14 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED ATIMHI R 0h R 0h Table 21 50 SAPHATIMHI SAPH_AATIMHI Register Field Descriptions Bit Field Type Reset Description 15 4 RESERVED R 0h 3 0 ATIMHI R ...

Страница 568: ...ts Incorporated Sigma Delta High Speed SDHS Chapter 22 SLAU367P October 2012 Revised April 2020 Sigma Delta High Speed SDHS This chapter describes the operation of the SDHS module Topic Page 22 1 Introduction 569 22 2 SDHS Functional Operation 569 22 3 Interrupts 594 22 4 Debug Mode 594 22 5 SDHS Registers 595 ...

Страница 569: ... amplifier PGA the sigma delta high speed SDHS and the data transfer controller DTC see Figure 22 1 PGA block Applies a gain to the input signal before the SDHS SDHS block ADC converts that converts the input signal to digital data at the programmed sampling rate DTC block Transfers the output data from the SDHS to the LEA RAM for data processing NOTE Naming convention for register names and bit f...

Страница 570: ... The modulator performs oversampling up to 80 MHz against the analog input signal and feeds the digital filter a pulse code modulated PCM data stream The digital filter averages the bitstreams from the modulator over a given number of bits and generates output data at a reduced sampling rate specified by the oversampling rate OSR for further data processing Averaging can be used to increase the si...

Страница 571: ...gure 22 3 Sigma Delta Principle 22 2 3 Digital Output The SDHS digital filter processes the data stream from the modulator The filter consists of two stages The first stage is a 7th order CIC filter CIC7 which is always enabled and its decimation ratio is 10 The second stage filter is a 1st order CIC filter CIC1 which is automatically enabled when the OSR ratio is greater than 10 The second stage ...

Страница 572: ...ww ti com 572 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sigma Delta High Speed SDHS Figure 22 4 CIC7 Filter Structure The transfer function is described in the z domain by Equation 11 11 The transfer function is described in the frequency domain by Equation 12 where OSR The ratio of the modulator frequency fM to the sa...

Страница 573: ...cascading the CIC7 and CIC1 filters the OSR ratio can be 10 20 40 80 or 160 22 2 3 3 Digital Filter Output Figure 22 7 shows the block diagram of the SDHS digital filter The CIC7 is a 7th order CIC filter with decimation of 10 The CIC1 is a 1st order CIC filter with programmable decimation of 2 4 8 or 16 By cascading the two filters OSR of 10 20 40 80 or 160 is offered The OSR ratio is configured ...

Страница 574: ...ber 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sigma Delta High Speed SDHS Figure 22 8 SDHS Filter Frequency Response SDHSCTL1 OSR 20 Figure 22 9 shows the frequency response of cascading CIC7 and CIC1 within fs normalized when SDHSCTL1 OSR 20 Figure 22 9 SDHS Filter Frequency Response Within fs SDHSCTL1 OSR 20 Figure 22 10 shows the fr...

Страница 575: ...back Copyright 2012 2020 Texas Instruments Incorporated Sigma Delta High Speed SDHS Figure 22 10 SDHS Filter Frequency Response within fs SDHSCTL1 OSR 40 Figure 22 11 shows the frequency response of cascading CIC7 and CIC1 within fs normalized when SDHSCTL1 OSR 80 Figure 22 11 SDHS Filter Frequency Response within fs SDHSCTL1 OSR 80 Figure 22 12 shows the frequency response of cascading CIC7 and C...

Страница 576: ...BR bits Table 22 1 Data Format Format SDHSCTL0 DF MSEL Bit Alignment SDHSCTL0 DAL GN Bit Analog Input Data Output SDHSCTL0 OBR 0 12 Bit Data Output SDHSCTL0 OBR 1 13 Bit Data Output SDHSCTL0 OBR 2 14 Bit 2s Complement 0 Right Aligned 0 fs 2 0x7FF 0xFFF 0x1FFF 0 0 0 0 fs 2 0x800 0x1000 0x2000 Offset Binary 1 Right Aligned 0 fs 2 0xFFF 0x1FFF 0x3FFF 0 0x800 0x1000 0x2000 fs 2 0 0 0 The effective num...

Страница 577: ...1 10 0 4 8 12 1 5 3 2 6 9 7 13 11 10 OBR 1 SHIFT 0 DALGN 0 Filter Output SDHSDT Register 0 4 8 12 1 5 3 2 6 9 7 15 14 13 11 10 0 4 8 12 1 5 3 2 6 9 7 13 11 10 OBR 1 SHIFT 1 DALGN 0 Filter Output SDHSDT Register 0 4 8 12 1 5 3 2 6 9 7 15 14 13 11 10 0 4 8 12 1 5 3 2 6 9 7 13 11 10 OBR 2 SHIFT 0 DALGN 0 Filter Output SDHSDT Register www ti com SDHS Functional Operation 577 SLAU367P October 2012 Revi...

Страница 578: ...78 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sigma Delta High Speed SDHS Figure 22 14 Bits Selection From Filter to the Data Register SDHSCTL0 DALGN 1 22 2 4 Data Transfer Controller DTC and Internal Data Buffer The SDHS supports output data rates up to 8 Msps which is faster than the system DMA can support so the SDHS...

Страница 579: ...HSCTL0 DALGN and SDHSCTL0 OBR bits must not be changed The destination system memory is the LEA RAM which is part of system memory The DTC automatically recognize the base address of the LEA RAM in the target device Only offset address needs to be configured to SDHSDTCDA register Destination address LEA RAM base address offset address Offset address SDHSDTCDA register value x 2 for example if SDHS...

Страница 580: ...put gain can be adjusted by SDHSCTL6 PGA_GAIN 5 0 See Table 22 2 for the PGA gain table Table 22 2 PGA Gain Table SDHSCTL6 PGA_GAI N 5 0 Bits PGA Gain Typical dB Tolerance Shift Entire Table 00xxxxb 6 5 1 dB 1 dB 010000b 6 5 1 dB 1 dB 010001b 6 5 1 dB 1 dB 010010b 5 5 1 dB 1 dB 010011b 4 6 1 dB 1 dB 010100b 4 1 1 dB 1 dB 010101b 3 3 1 dB 1 dB 010110b 2 3 1 dB 1 dB 010111b 1 4 1 dB 1 dB 011000b 0 8...

Страница 581: ...0 1 dB 1 dB 101010b 13 9 1 dB 1 dB 101011b 14 9 1 dB 1 dB 101100b 15 5 1 dB 1 dB 101101b 16 3 1 dB 1 dB 101110b 17 2 1 dB 1 dB 101111b 18 2 1 dB 1 dB 110000b 18 8 1 dB 1 dB 110001b 19 6 1 dB 1 dB 110010b 20 5 1 dB 1 dB 110011b 21 5 1 dB 1 dB 110100b 22 0 1 dB 1 dB 110101b 22 8 1 dB 1 dB 110110b 23 6 1 dB 1 dB 110111b 24 6 1 dB 1 dB 111000b 25 0 1 dB 1 dB 111001b 25 8 1 dB 1 dB 111010b 26 7 1 dB 1 ...

Страница 582: ... Section 22 2 12 1 0 1 SDHSCTL4 SDH SON 0 1 SDHSCTL4 SDH SON 1 0 SDHSCTL5 SST ART 0 1 See Section 22 2 12 1 1 0 Not supported Not supported Not supported Not supported 1 1 1 ASQ_ACQARM 0 1 from ASQ ASQ_ACQARM 1 0 from ASQ ASQ_ACQTRIG 0 1 from ASQ See Section 22 2 12 0 x x Not supported Not supported Not supported Not supported 22 2 6 1 SDHS in Auto Mode and Register Mode The SDHS is one of the sub...

Страница 583: ...r See the following sequence for the correct SDHS configuration 1 Turn on the USS module and wait for UUPSCTL UPSTATE 3 2 Configure all registers except the SDHSCTL3 SDHSCTL4 and SDHSCTL5 registers no specific order is required SDHSCTL0 TRGSRC 0 3 Enable trigger sources Set SDHSCTL3 TRIGEN 1 4 Power up the SDHS Set SDHSCTL4 SDHSON 1 If SDHSCTL0 AUTOSSDIS 1 then the remaining steps are not required...

Страница 584: ...ion www ti com 584 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Sigma Delta High Speed SDHS Figure 22 18 SDHS Operation as Part of USS Measurement SDHSCTL0 TRGSRC 1 22 2 7 TRIGEN Bit and SDHS_LOCK Bit SDHSCTL3 TRIGEN has two functional roles The first role is to enable the SDHS to receive the power trigger and conversion ...

Страница 585: ...dating the PGA gain while SDHS is performing data conversion Expect a transition period before the new gain is applied see the device specific data sheet for the PGA gain settling time Table 22 5 SDHSCTL3 TRIGEN Bit and SDHSCTL5 SDHS_LOCK Bit Control Bit Type How to Set the Control Bit Registers Locked SDHSCTL3 TRIGEN Read Write Write 1 to SDHSCTL3 TRIGEN bit SDHSCTL0 SDHSCTL1 SDHSCTL2 SDHSCTL7 SD...

Страница 586: ... ACQDONE Interrupt SDHS is Power Off SDHS Settling Time First Sample Conversion Stop Last Sample Sample Sample SDHS Power Off ACQDONE Interrupt SSTRG Interrupt Conversion Start SSTRG Interrupt Conversion Conversion Conversion Conversion Conversion Conversion SDHS Functional Operation www ti com 586 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Ins...

Страница 587: ...Power On SDHSCTL0 AUTOSSDIS 1 and SDHSCTL2 SMPCTLOFF 1 SDHSCTL5 SDHS_LOCK bit Read Only SDHSCTL3 TRIGEN bit Conversion Start SSTRG Interrupt ACQDONE Interrupt Conversion Start SSTRG Interrupt SDHSCTL4 SDHSON or ASQ_ACQARM SDHSCTL5 SSTART or ASQ_ACQTRG Required Settling Time Conversion Conversion Conversion Conversion Conversion Conversion First Sample www ti com SDHS Functional Operation 587 SLAU3...

Страница 588: ...nversion start signal Auto conversion start enabled 0 SDHSCTL4 SD HSON 1 ASQ_ACQARM 1 from ASQ Not Required Not Required Data conversion automatically begins after power up The SDHS settling time is automatically applied When SDHSCTL0 AUTOSSDIS 0 automatic conversion start is enabled Conversion automatically starts after the SDHS is powered on During power up the SDHS settling time is monitored an...

Страница 589: ...ersion Start and Stop When SDHSCTL0 AUTOSSDIS 1 22 2 9 INTDLY Interrupt Delay bits After conversion start the position of the first output data to the internal data buffer and the first SDHSRIS DTRDY interrupt can be adjusted by the SDHSCTL0 INTDLY delay Any skipped data is permanently lost The delay is applied each time conversion starts The SDHSRIS OVF overflow interrupt is not enabled for the s...

Страница 590: ... 2 80 2nd sample 1 160 2nd sample 1 22 2 10 Total Sample Size The total number of samples that the SDHS generates can be predefined by SDHSCTL2 SMPSZ when SDHSCTL2 SMPCTLOFF 0 The value written to SDHSCTL2 SMPSZ includes the samples skipped by SDHSCTL0 INTDLY Total number of samples SDHS generates SMPSZ 1 when SDHSCTL2 SMPCTLOFF 0 The number of samples that can be read or transferred SMPSZ INTDLY ...

Страница 591: ...owered down 2 sample periods must pass before starting a new data conversion or turning SDHS on see Figure 22 24 and Figure 22 25 SDHS output sampling period SDHSCTL1 OSR PLL output clock frequency SDHS modulator sampling frequency SDHS output sampling frequency PLL output clock frequency SDHS modulator sampling frequency SDHSCTL1 OSR 22 2 11 Window Comparator The window comparator can monitor dat...

Страница 592: ...ange SDHS_ACQDONE to ASQ Assert SDHSRIS ACQDONE Assert Don t care Don t care 1 Not supported The ASQ stops the SDHS operation ACQ_SDHSSTOP 0 1 caused by UUPSCTL USSSTOP 0 1 UUPSCTL USSPWRDN 0 1 SAPHASCTL0 STOP 0 1 Enter debug mode while the SDHS is performing data conversion Don t care Don t care Don t care SDHS power No change Data conversion Stop SDHSRIS ISTOP Assert SDHS_ACQDONE to ASQ Assert S...

Страница 593: ...r No change Data conversion Stop SDHSRIS ISTOP Assert SDHS_ACQDONE to ASQ Assert SDHSRIS ACQDONE Assert 1 SDHS power No change Data conversion Stop SDHSRIS ISTOP No change SDHS_ACQDONE to ASQ Assert SDHSRIS ACQDONE Assert The stop conditions listed in Table 22 9 can occur when data conversion has already completed or has not started Table 22 10 summarizes how the SDHS responds to the signals when ...

Страница 594: ... in the SDHSWINHITH register SDHSRIS WINHL window low interrupt This bit is asserted when a new output data is lower than the value in the SDHSWINLOTH register In addition the SDHSRIS ISTOP incomplete stop status bit is asserted when the data conversion has been interrupted without completion This bit is not an interrupt flag It can be used as a status bit not an interrupt flag 22 3 1 IIDX Interru...

Страница 595: ...SDHS_PWR_UP signal should be de asserted first then SDHSCTL3 TRIGEN bit needs to be cleared to be zero Table 22 11 SDHS Registers Offset Acronym Register Name Type Reset Section 0h SDHSIIDX Interrupt Index Register read only 0h Section 22 5 1 2h SDHSMIS Masked Interrupt Status and Clear Register read only 0h Section 22 5 2 4h SDHSRIS Raw Interrupt Status Register read only 0h Section 22 5 3 6h SDH...

Страница 596: ...vice routine handling On each read only one interrupt is indicated On a read the current interrupt highest priority is automatically de asserted by the hardware and the corresponding bit in RIS and MISC are de asserted as well After a read from the CPU not from the debug interface the register is updated with the next highest priority interrupt if none are pending then it is read as zero If the in...

Страница 597: ... 6 Reserved R 0h Reserved Always reads as 0 5 WINLO R 0h SDHS Window Low Masked Interrupt Status bit Reset type PUC 0h R No interrupt pending 1h R Interrupt pending 4 WINHI R 0h SDHS Window High Masked Interrupt Status bit Reset type PUC 0h R No interrupt pending 1h R Interrupt pending 3 DTRDY R 0h SDHS Data Ready Masked Interrupt Status bit Reset type PUC 0h R No interrupt pending 1h R Interrupt ...

Страница 598: ...to SDHSICR ISTOP bit Reset type PUC 0h R No ISTOP event 1h R Conversion has been interrupted and stopped before completing the number of samples defined in SDHSCTL2 SAMPSZ 14 6 Reserved R 0h Reserved Always reads as 0 5 WINLO R 0h SDHS Window Low Raw Interrupt Status bit Read Only This bit is asserted when output data value is lower than the value in the SDHSWINLOTH register Note 1 The window comp...

Страница 599: ...Y event 1h R The data buffer has become empty 2 SSTRG R 0h SDHS Conversion Start Trigger Raw Interrupt Status bit Read Only Reset type PUC 0h R No SSTRG event 1h R Converson Start signal has been asserted 1 ACQDONE R 0h Acquisition Done Raw Interrupt Status bit Read Only This bit is not de asserted by hardware This bit is asserted when data conversion is ended either complete or incomplete If SDHS...

Страница 600: ... that this interrupt is always disabled No interrupt will be generated 14 6 Reserved R 0h Reserved Always reads as 0 5 WINLO R W 0h SDHS Window Low Interrupt Mask bit Reset type PUC 0h R W Interrupt is disabled 1h R W Interrupt is enabled 4 WINHI R W 0h SDHS Window High Interrupt Mask bit Reset type PUC 0h R W Interrupt is disabled 1h R W Interrupt is enabled 3 DTRDY R W 0h SDHS Data Ready Interru...

Страница 601: ...INHI DTRDY SSTRG ACQDONE OVF R 0h W 0h W 0h W1S 0h W 0h W 0h W 0h Table 22 16 SDHSICR Register Field Descriptions Bit Field Type Reset Description 15 ISTOP W 0h Incomplete Stop Interrupt Clear bit 14 6 Reserved R 0h Reserved Always reads as 0 5 WINLO W 0h SDHS Window Low Interrupt Clear bit 4 WINHI W 0h SDHS Window High Interrupt Clear bit Reset type PUC 3 DTRDY W1S 0h SDHS Data Ready Interrupt Cl...

Страница 602: ...S 0h W 0h W 0h W 0h Table 22 17 SDHSISR Register Field Descriptions Bit Field Type Reset Description 15 ISTOP W 0h Incomplete Stop Interrupt Set bit 14 6 Reserved R 0h Reserved Always reads as 0 5 WINLO W 0h SDHS Window Low Interrupt Set bit 4 WINHI W 0h SDHS Window High Interrupt Set bit Reset type PUC 3 DTRDY W1S 0h SDHS Data Ready Interrupt Set bit Write 1 to set SDHSRIS DTRDY bit Note This bit...

Страница 603: ...HS Descriptor Register L Figure 22 33 SDHSDESCLO Register 15 14 13 12 11 10 9 8 FEATUREVER INSTNUM R 0h R 1h 7 6 5 4 3 2 1 0 MAJREV MINREV R 1h R 0h Table 22 18 SDHSDESCLO Register Field Descriptions Bit Field Type Reset Description 15 12 FEATUREVER R 0h Feature Set for the module Reset type PUC 11 8 INSTNUM R 1h Instance Number within the device This will be a parameter to the RTL for modules tha...

Страница 604: ...8 SDHSDESCHI Register Offset Eh reset BB10h SDHSDESCHI is shown in Figure 22 34 and described in Table 22 19 Return to Summary Table SDHS Descriptor Register H Figure 22 34 SDHSDESCHI Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 MODULEID R BB10h Table 22 19 SDHSDESCHI Register Field Descriptions Bit Field Type Reset Description 15 0 MODULEID R BB10h Module Identifier Reset type PUC ...

Страница 605: ... control mode SDHSCTL4 SDHSON is the source of the SHDS_PWR_UP DOWN signal SDHSCTL5 SSTART is the source of the CONVERSION_START STOP signal 1h R W ASQ control mode The SDHS is controlled by the ASQ ASQ_ACQARM signal from the ASQ is the source of the SHDS_PWR_UP DOWN signal ASQ_ACQTRIG signal from the ASQ is the source of the CONVERSION_START STOP signal 14 Reserved R 0h Reserved Always reads as 0...

Страница 606: ...ple delay 2nd sample is the first interrupt 2h R W 2 samples delay 3rd sample is the first interrupt 3h R W 3 samples delay 4rd sample is the first interrupt 4h R W 4 samples delay 5th sample is the first interrupt 5h R W 5 samples delay 6th sample is the first interrupt 6h R W 6 samples delay 7th sample is the first interrupt 7h R W 7 samples delay 8th sample is the first interrupt 0 AUTOSSDIS R ...

Страница 607: ...SCTL3 TRGEN 1 or SDHSCTL5 SDHS_LOCK 1 this register is locked In that case an attempt to update this registers will be ignored Figure 22 36 SDHSCTL1 Register 15 14 13 12 11 10 9 8 Reserved R 0h 7 6 5 4 3 2 1 0 Reserved OSR R 0h R W 0h Table 22 21 SDHSCTL1 Register Field Descriptions Bit Field Type Reset Description 15 4 Reserved R 0h Reserved Always reads as 0 3 0 OSR R W 0h Over Sampling Rate Out...

Страница 608: ...ow interrupt flag SDHSRIS OVF will eventually be asserted 14 WINCMPEN R W 0h Window Comparator Enable Note For the samples skipped by SDHSCTL0 INTDLY window comparison is not applied Window comparison is performed with the latest conversion result before it is pushed to the internal buffer Window comparison is still functional when the internal buffer is full Reset type PUC 0h R W Window Comparato...

Страница 609: ... Trigger Source and lock SDHS registers Note This bit is used to inform SDHS that register configuration has been completed This bit must be written as 1 before applying SDHS_PWR_UP signal Once this bit is asserted SDHSCTL0 SDHSCTL1 SDHSCTL2 SDHSCTL7 SDHSWINHITH SDHSWINLOTH and SDHSDTCDA registers are locked not allowed to be modified This bit is locked once a SDHS_PWR_UP signal is applied See SDH...

Страница 610: ...1 0 RESERVED SDHSON R 0h R W 0h Table 22 24 SDHSCTL4 Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R 0h Reserved Always reads as 0 0 SDHSON R W 0h Turn on the SDHS module When SDHSCTL0 TRGSRC 0 SDHS Power up down bit Note When SDHSCTL0 AUTOSSDIS 0 and SDHSCTL0 TRGSRC 0 the SDHSON bit only powers up the SDHS does not start sampling When SDHSCTL0 AUTOSSDIS 1 and SDHSCTL0...

Страница 611: ...erted immediately In order to update SDHS registers clear SDHSCTL4 SDHSON first and then SDHSCTL3 TRIGEN needs to be cleared 2 When SDHSCTL0 TRGSRC 1 It takes up to 4 system clock cycles to assert SDHSCTL5 SDHS_LOCK after detecting the SDHS_PWR_UP signal ASQ_ACQARM from the ASQ In order to update SDHS registers the SDHS_PWR_UP signal should be de asserted first by the ASQ then SDHSCTL3 TRIGEN need...

Страница 612: ...t Description 0 SSTART R W 0h Start data conversion Note When SDHSCTL0 AUTOSSDIS 0 and SDHSCTL0 TRGSRC 0 the SDHSON powers up the SDHS the SSTART triggers data conversion It is very important to wait for the SDHS settling time 34 usec before asserting SSTART from the time of SDHSON 0 1 When SDHSCTL0 AUTOSSDIS 1 and SDHSCTL0 TRGSRC 0 this bit is invalid When SDHSCTL0 TRGSRC 1 this bit is invalid Re...

Страница 613: ...nd described in Table 22 26 Return to Summary Table SDHS Control Register 6 Figure 22 41 SDHSCTL6 Register 15 14 13 12 11 10 9 8 Reserved R 0h 7 6 5 4 3 2 1 0 Reserved PGA_GAIN R 0h R W 19h Table 22 26 SDHSCTL6 Register Field Descriptions Bit Field Type Reset Description 15 6 Reserved R 0h Reserved Always reads as 0 5 0 PGA_GAIN R W 19h PGA Gain Control bits These bits control the Gain range of th...

Страница 614: ... 13 12 11 10 9 8 RESERVED R 0h 7 6 5 4 3 2 1 0 RESERVED MODOPTI R 0h R W Fh Table 22 27 SDHSCTL7 Register Field Descriptions Bit Field Type Reset Description 15 5 RESERVED R 0h Reserved Always reads as 0 4 0 MODOPTI R W Fh SDHS Modulator Optimization bits In order to get the maximum performance of SDHS it is recommened to configure this bits based on the PLL output frequency See below for details ...

Страница 615: ...ed SDHS 22 5 17 SDHSDT Register Offset 22h reset 0h SDHSDT is shown in Figure 22 43 and described in Table 22 28 Return to Summary Table SDHS Data Converstion Register Figure 22 43 SDHSDT Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 SDHSDT R 0h Table 22 28 SDHSDT Register Field Descriptions Bit Field Type Reset Description 15 0 SDHSDT R 0h Conversion Data Reset type PUC ...

Страница 616: ...registers will be ignored Figure 22 44 SDHSWINHITH Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 WINHITH R W 0h Table 22 29 SDHSWINHITH Register Field Descriptions Bit Field Type Reset Description 15 0 WINHITH R W 0h SDHS Window Comparator High Threshold Register The user always needs to ensure that the values in this register is in the correct data format When the conversion data is higher than ...

Страница 617: ...is registers will be ignored Figure 22 45 SDHSWINLOTH Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 WINLOTH R W 0h Table 22 30 SDHSWINLOTH Register Field Descriptions Bit Field Type Reset Description 15 0 WINLOTH R W 0h SDHS Window Comparator Low Threshold Register The user always needs to ensure that the values in this register is in the correct data format When the conversion data is lower than...

Страница 618: ...n that case an attempt to update this registers will be ignored Figure 22 46 SDHSDTCDA Register 15 14 13 12 11 10 9 8 Reserved DTCDA R 0h R W 0h 7 6 5 4 3 2 1 0 DTCDA R W 0h Table 22 31 SDHSDTCDA Register Field Descriptions Bit Field Type Reset Description 15 Reserved R 0h Reserved Always reads as 0 14 0 DTCDA R W 0h DTC destination offset address Destination location base address DTCDA x 2 The ad...

Страница 619: ...nts Incorporated Metering Test Interface MTIF Chapter 23 SLAU367P October 2012 Revised April 2020 Metering Test Interface MTIF This chapter describes the MSP430 Metering Test Interface MTIF module Topic Page 23 1 MTIF Introduction 620 23 2 MTIF Operation 621 23 3 MTIF Block Diagram 624 23 4 MTIF Registers 625 ...

Страница 620: ... current consumption measured by the meter MTIF provides three independent password controlled access ports One for the pulse generator one for the pulse counter and one for configuration and maintenance Because all three passwords are different a clear software separation can be achieved Figure 23 1 shows an assumed software stack of a meter that is divided into smaller blocks thus allowing certi...

Страница 621: ... 17 17 17 pulses inside MTIF ouput enable MTIF output Consumption normalized to units 1 2 3 4 5 6 pulse grid frequency 0 www ti com MTIF Operation 621 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Metering Test Interface MTIF Figure 23 2 MTIF Pulse Diagram 23 2 MTIF Operation The MTIF module can be configured in active mod...

Страница 622: ...s before frame end 128 Hz 4 128 1 s 4 ms before frame end 256 Hz 5 256 500 ms 2 ms before frame end 512 Hz 6 512 250 ms 1 ms before frame end 1024 Hz 7 1024 125 ms 500 µs before frame end 2048 Hz Table 23 2 MTIF Initialization Order Required Comment 1 Configure and enable the RTC See RTC module chapter for details 2 Write to MTIFPGCNF PGPW 0x5A PGFS 5 PGCLR 1 PGEN 1 Set grid frequency to 256 Hz cl...

Страница 623: ...r is updated much faster than the pulse generator frame frequency the value read during the update time slot is used for the next frame 23 2 6 Various Resets During MTIF Operation The MTIF module provides immunity against most system reset types A power up clear PUC resets the watchdog timer WDT and password violation resets do not cause any changes in setting count and behavior of the MTIF settin...

Страница 624: ... generator is cleared when the pulse generator is disabled After the application enables MTIFPGCTL PGEN the pulse generation starts after 2 to 3 cycles with the LF clock at 32 kHz Even though the pulse counter may be cleared independent of MTIFPGCTL PCEN make sure that the counter is cleared either before or after 2 to 3 LFCLK cycles to avoid conflicts The pulse counter increments on high active p...

Страница 625: ...MTIFPGCNF Pulse Generator Configuration Register read write 6970h Section 23 4 1 2h MTIFPGKVAL Pulse Generator Value Register read write 6900h Section 23 4 2 4h MTIFPGCTL Pulse Generator Control Register read write 6900h Section 23 4 3 6h MTIFPGSR Pulse Generator Status Register read write 0h Section 23 4 4 8h MTIFPCCNF Pulse Counter Configuration Register read write 9600h Section 23 4 5 Ah MTIFPC...

Страница 626: ...rid frequency select This value determines at which time grid pulses are generated The pulse generator frame frequency is an 1 256th of this MTIFPGCNF PGEN has to be one to perform a change Reset type PUC 0h R W Pulse grid frequency is set to 8 Hz nominal 1h R W Pulse grid frequency is set to 16 Hz nominal 2h R W Pulse grid frequency is set to 32 Hz nominal 3h R W Pulse grid frequency is set to 64...

Страница 627: ...able 23 7 MTIFPGKVAL Register Field Descriptions Bit Field Type Reset Description 15 8 PGPW R W 69h PG password Always reads as 0x69 Must be written as 0x5A for register changes to be effective This password differs from the pin configuration and pulse counter passwords Reset type PUC 5Ah W PGPW Must be written as 0x5A for register changes to be effective 69h R PGPW_R Read value while locked 7 RES...

Страница 628: ...sword Always reads as 0x69 Must be written as 0x5A for register changes to be effective This password differs from the pin configuration and pulse counter passwords Reset type PUC 5Ah W PGPW Must be written as 0x5A for register changes to be effective 69h R PGPW_R Read value while locked 7 2 RESERVED R W 0h 1 PGUR RH W1S 0h Pulse Grid Frequency Update Request with password protection as in MTIFPGC...

Страница 629: ...ister Figure 23 8 MTIFPGSR Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED PGUA PKUA R W 0h RH W 0h RH W 0h Table 23 9 MTIFPGSR Register Field Descriptions Bit Field Type Reset Description 15 2 RESERVED R W 0h 1 PGUA RH W 0h Pulse Grid Frequency Update Acknowledge This acknowledges a MTIFPGSR PGUR 2 3 LFCLK cycles after the PGFS has been updated Reset type PUC 0 PKUA RH W 0...

Страница 630: ...96h Pulse counter password Always reads as 0x96 Must be written as 0xA5 for register changes to be effective This password differs from the pin configuration and pulse generator passwords Reset type PUC 96h R PCPW_R Read value while locked A5h W PCPW 0xA5 7 3 RESERVED R W 0h 2 PCCLR RH W1S 0h Pulse counter clear This bit allows to clear the pulse counter when set to one MTIFPCCNF PCEN has to be on...

Страница 631: ...gister Offset Ah reset 0h MTIFPCR is shown in Figure 23 10 and described in Table 23 11 Return to Summary Table Pulse Counter Value Register Figure 23 10 MTIFPCR Register 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 PCR RH Table 23 11 MTIFPCR Register Field Descriptions Bit Field Type Reset Description 15 0 PCR RH 0 Pulse Counter value register This register returns the count value from the pulse counter...

Страница 632: ...ure 23 11 and described in Table 23 12 Return to Summary Table Pulse Counter Control Register Figure 23 11 MTIFPCCTL Register 15 14 13 12 11 10 9 8 RESERVED R W 0h 7 6 5 4 3 2 1 0 RESERVED PCRR R W 0h RH W1S 0h Table 23 12 MTIFPCCTL Register Field Descriptions Bit Field Type Reset Description 15 1 RESERVED R W 0h 0 PCRR RH W1S 0h Pulse Counter Read Request Set this to request an update of MTIFPCR ...

Страница 633: ...H W 0h RH W 0h Table 23 13 MTIFPCSR Register Field Descriptions Bit Field Type Reset Description 15 2 RESERVED R W 0h 1 PCOFL RH W 0h Pulse counter overflow This bit indicates an overflow of the pulse counter when its value changes since the last read request procedure It is basically the 17th bit of the counter Reset type PUC 0 PCRA RH W 0h Pulse counter read acknowledge This acknowledges the upd...

Страница 634: ...e pulse generator and pulse counter passwords Reset type PUC 0Fh R TPPW_R Read value while locked C3h W TPPW 0xC3 7 4 RESERVED R W 0h 3 ACTIVATE R W 0h Test port terminal enable activation This value determines if the testport output is enabled solely by software or by software and hardware Reset type POR 0h R W The test port output is enabled solely by TPOE enabled if MTIFTPCTL TPOE 1 1h R W The ...

Страница 635: ...er 24 SLAU367P October 2012 Revised April 2020 Watchdog Timer WDT_A The watchdog timer is a 32 bit timer that can be used as a watchdog or as an interval timer This chapter describes the watchdog timer The enhanced watchdog timer WDT_A is implemented in all devices Topic Page 24 1 WDT_A Introduction 636 24 2 WDT_A Operation 638 24 3 WDT_A Registers 640 ...

Страница 636: ...e configured as an interval timer and can generate interrupts at selected time intervals Features of the watchdog timer module include Eight software selectable time intervals Watchdog mode Interval mode Password protected access to Watchdog Timer Control WDTCTL register Selectable clock source Can be stopped to conserve power Clock fail safe feature The watchdog timer block diagram is shown in Fi...

Страница 637: ...ulse Generator VLOCLK Clock Request Logic X_CLK request SMCLK request ACLK request VLOCLK request 10 11 Q9 Q13 Q15 Q19 Q23 Q27 Q31 X_CLK 11 10 01 00 11 10 01 00 0 1 16 bit Counter CLK 32 bit WDT extension www ti com WDT_A Introduction 637 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Watchdog Timer WDT_A Figure 24 1 Watchd...

Страница 638: ...nterval Timer Mode Setting the WDTTMSEL bit to 1 selects the interval timer mode This mode can be used to provide periodic interrupts In interval timer mode the WDTIFG flag is set at the expiration of the selected time interval A PUC is not generated in interval timer mode at expiration of the selected timer interval and the WDTIFG enable bit WDTIE remains unchanged When the WDTIE bit and the GIE ...

Страница 639: ...ilable in different low power modes The requirements of the application and the type of clocking that is used determine how the WDT_A should be configured For example the WDT_A should not be configured in watchdog mode with a clock source that is originally sourced from DCO XT1 in high frequency mode or XT2 sourcing SMCLK or ACLK if the user wants to use low power mode 3 In this case SMCLK or ACLK...

Страница 640: ...The watchdog timer module registers are listed in Table 24 1 The base address for the watchdog timer module registers and special function registers SFRs can be found in the device specific data sheets The address offset is given in Table 24 1 Table 24 1 WDT_A Registers Offset Acronym Register Name Type Access Reset Section 00h WDTCTL Watchdog Timer Control Read write Word 6904h Section 24 3 1 ...

Страница 641: ...imer is stopped 6 5 WDTSSEL RW 0h Watchdog timer clock source select 00b SMCLK 01b ACLK 10b VLOCLK 11b X_CLK same as VLOCLK if not defined differently in data sheet 4 WDTTMSEL RW 0h Watchdog timer mode select 0b Watchdog mode 1b Interval timer mode 3 WDTCNTCL RW 0h Watchdog timer counter clear Setting WDTCNTCL 1 clears the count value to 0000h WDTCNTCL is automatically reset 0b No action 1b WDTCNT...

Страница 642: ... 2012 Revised April 2020 Timer_A Timer_A is a 16 bit timer and counter with multiple capture compare registers There can be multiple Timer_A modules on a given device see the device specific data sheet This chapter describes the operation and use of the Timer_A module Topic Page 25 1 Timer_A Introduction 643 25 2 Timer_A Operation 645 25 3 Timer_A Registers 657 ...

Страница 643: ...nfigurable capture compare registers Configurable outputs with pulse width modulation PWM capability Asynchronous input and output latching Interrupt vector register for fast decoding of all Timer_A interrupts The block diagram of Timer_A is shown in Figure 25 1 NOTE Use of the word count Count is used throughout this chapter It means the counter must be in the process of counting for the action t...

Страница 644: ...mer Clock EQU0 Timer Clock Timer Clock TAxCCR6 SCCI Y A EN CCR1 POR TACLR CCR0 Timer Block 00 01 10 11 Set TAxCCR6 CCIFG CAP 1 0 1 0 CCR2 CCR3 ACLK SMCLK TAxCLK INCLK IDEX Divider 1 8 CCR4 CCR5 2 2 3 2 2 2 3 Copyright 2016 Texas Instruments Incorporated Timer_A Introduction www ti com 644 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments I...

Страница 645: ...ng and a majority vote taken in software to determine the correct reading Any write to TAxR takes effect immediately 25 2 1 1 Clock Source Select and Divider The timer clock can be sourced from ACLK SMCLK or externally from TAxCLK or INCLK The clock source is selected with the TASSEL bits The selected clock source may be passed directly to the timer or divided by 2 4 or 8 using the ID bits The sel...

Страница 646: ...Fh counts The timer repeatedly counts up to the value of compare register TAxCCR0 which defines the period see Figure 25 2 The number of timer counts in the period is TAxCCR0 1 When the timer value equals TAxCCR0 the timer restarts counting from zero If up mode is selected when the timer value is greater than TAxCCR0 the timer immediately restarts counting from zero Figure 25 2 Up Mode The TAxCCR0...

Страница 647: ...he TAIFG interrupt flag is set when the timer counts from 0FFFFh to zero Figure 25 5 shows the flag set cycle Figure 25 5 Continuous Mode Flag Setting 25 2 3 3 Use of Continuous Mode The continuous mode can be used to generate independent time intervals and output frequencies Each time an interval is completed an interrupt is generated The next time interval is added to the TAxCCRn register in the...

Страница 648: ...it was counting before it was stopped If this is not desired the TACLR bit must be set to clear the direction Setting TACLR also clears the TAR value and the clock divider counter logic the divider setting remains unchanged In up down mode the TAxCCR0 CCIFG interrupt flag and the TAIFG interrupt flag are set only once during a period separated by one half the timer period The TAxCCR0 CCIFG interru...

Страница 649: ...25 2 4 Capture Compare Blocks Up to seven identical capture compare blocks TAxCCRn where n 0 to 7 are present in Timer_A Any of the blocks may be used to capture the timer data or to generate time intervals 25 2 4 1 Capture Mode The capture mode is selected when CAP 1 Capture mode is used to record time events It can be used for speed computations or time measurements The capture inputs CCIxA and ...

Страница 650: ...ght 2012 2020 Texas Instruments Incorporated Timer_A Figure 25 10 Capture Signal SCS 1 NOTE Changing Capture Inputs Changing capture inputs while in capture mode may cause unintended capture events To avoid this scenario capture inputs should only be changed when capture mode is disabled CM 0 or CAP 0 Overflow logic is provided in each capture compare register to indicate if a second capture was p...

Страница 651: ...ignals such as PWM signals Each output unit has eight operating modes that generate signals based on the EQU0 and EQUn signals 25 2 5 1 Output Modes The output modes are defined by the OUTMOD bits and are described in Table 25 2 The OUTn signal is changed with the rising edge of the timer clock for all modes except mode 0 Output modes 2 3 6 and 7 are not useful for output unit 0 because EQUn EQU0 ...

Страница 652: ... Timer_A Operation www ti com 652 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Timer_A 25 2 5 1 1 Output Example Timer in Up Mode The OUTn signal is changed when the timer counts up to the TAxCCRn value and rolls from TAxCCR0 to zero depending on the output mode An example is shown in Figure 25 12 using TAxCCR0 and TAxCCR...

Страница 653: ...ww ti com Timer_A Operation 653 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Timer_A 25 2 5 1 2 Output Example Timer in Continuous Mode The OUTn signal is changed when the timer reaches the TAxCCRn and TAxCCR0 values depending on the output mode An example is shown in Figure 25 13 using TAxCCR0 and TAxCCR1 Figure 25 13 Ou...

Страница 654: ...Tn signal changes when the timer equals TAxCCRn in either count direction and when the timer equals TAxCCR0 depending on the output mode An example is shown in Figure 25 14 using TAxCCR0 and TAxCCR2 Figure 25 14 Output Example Timer in Up Down Mode NOTE Switching between output modes When switching between output modes one of the OUTMOD bits should remain set during the transition unless switching...

Страница 655: ... The TAxCCR0 CCIFG flag is automatically reset when the TAxCCR0 interrupt request is serviced Figure 25 15 Capture Compare TAxCCR0 Interrupt Flag 25 2 6 2 TAxIV Interrupt Vector Generator The TAxCCRy CCIFG flags and TAIFG flags are prioritized and combined to source a single interrupt vector The interrupt vector register TAxIV is used to determine which flag requested an interrupt The highest prio...

Страница 656: ...CCR6 16 cycles Timer overflow TA0IFG 14 cycles Interrupt handler for TA0CCR0 CCIFG Cycles CCIFG_0_HND Start of handler Interrupt latency 6 RETI 5 Interrupt handler for TA0IFG TA0CCR1 through TA0CCR6 CCIFG TA0_HND Interrupt latency 6 ADD TA0IV PC Add offset to Jump table 3 RETI Vector 0 No interrupt 5 JMP CCIFG_1_HND Vector 2 TA0CCR1 2 JMP CCIFG_2_HND Vector 4 TA0CCR2 2 JMP CCIFG_3_HND Vector 6 TA0...

Страница 657: ...h Section 25 3 3 0Ah TAxCCTL4 Timer_Ax Capture Compare Control 4 Read write Word 0000h Section 25 3 3 0Ch TAxCCTL5 Timer_Ax Capture Compare Control 5 Read write Word 0000h Section 25 3 3 0Eh TAxCCTL6 Timer_Ax Capture Compare Control 6 Read write Word 0000h Section 25 3 3 10h TAxR Timer_Ax Counter Read write Word 0000h Section 25 3 2 12h TAxCCR0 Timer_Ax Capture Compare 0 Read write Word 0000h Sect...

Страница 658: ...t divider These bits along with the TAIDEX bits select the divider for the input clock 00b 1 01b 2 10b 4 11b 8 5 4 MC RW 0h Mode control Setting MC 00h when Timer_A is not in use conserves power 00b Stop mode Timer is halted 01b Up mode Timer counts up to TAxCCR0 10b Continuous mode Timer counts up to 0FFFFh 11b Up down mode Timer counts up to TAxCCR0 then down to 0000h 3 Reserved RW 0h Reserved 2...

Страница 659: ... Timer_A 25 3 2 TAxR Register Timer_Ax Counter Register Figure 25 17 TAxR Register 15 14 13 12 11 10 9 8 TAxR rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 TAxR rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 25 5 TAxR Register Description Bit Field Type Reset Description 15 0 TAxR RW 0h Timer_A register The TAxR register is the count of Timer_A ...

Страница 660: ...ions 00b CCIxA 01b CCIxB 10b GND 11b VCC 11 SCS RW 0h Synchronize capture source This bit is used to synchronize the capture input signal with the timer clock 0b Asynchronous capture 1b Synchronous capture 10 SCCI RW 0h Synchronized capture compare input The selected CCI input signal is latched with the EQUx signal and can be read from this bit 9 Reserved R 0h Reserved Reads as 0 8 CAP RW 0h Captu...

Страница 661: ...ed Timer_A Table 25 6 TAxCCTLn Register Description continued Bit Field Type Reset Description 1 COV RW 0h Capture overflow This bit indicates a capture overflow occurred COV must be reset with software 0b No capture overflow occurred 1b Capture overflow occurred 0 CCIFG RW 0h Capture compare interrupt flag 0b No interrupt pending 1b Interrupt pending ...

Страница 662: ...ure is performed 25 3 5 TAxIV Register Timer_Ax Interrupt Vector Register Figure 25 20 TAxIV Register 15 14 13 12 11 10 9 8 TAIV r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 TAIV r0 r0 r0 r0 r 0 r 0 r 0 r0 Table 25 8 TAxIV Register Description Bit Field Type Reset Description 15 0 TAIV R 0h Timer_A interrupt vector value 00h No interrupt pending 02h Interrupt Source Capture compare 1 Interrupt Flag TAx...

Страница 663: ...mer divider logic Figure 25 21 TAxEX0 Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved TAIDEX 1 r0 r0 r0 r0 r0 rw 0 rw 0 rw 0 Table 25 9 TAxEX0 Register Description Bit Field Type Reset Description 15 3 Reserved R 0h Reserved Reads as 0 2 0 TAIDEX RW 0h Input divider expansion These bits along with the ID bits select the divider for the input clock 000b Divi...

Страница 664: ...er 2012 Revised April 2020 Timer_B Timer_B is a 16 bit timer counter with multiple capture compare registers There can be multiple Timer_B modules on a given device see the device specific data sheet This chapter describes the operation and use of the Timer_B module Topic Page 26 1 Timer_B Introduction 665 26 2 Timer_B Operation 667 26 3 Timer_B Registers 680 ...

Страница 665: ...er for fast decoding of all Timer_B interrupts The block diagram of Timer_B is shown in Figure 26 1 NOTE Use of the word count Count is used throughout this chapter It means the counter must be in the process of counting for the action to take place If a particular value is directly written to the counter an associated action does not take place NOTE Nomenclature There may be multiple instantiatio...

Страница 666: ...CCR6 RC 10 12 16 8 TBCLGRP CCR5 CCR4 CCR1 Group Load Logic Group Load Logic TBSSEL 00 01 10 11 GND VCC CCI6A CCI6B 00 01 10 11 CCIS 00 01 10 11 00 01 10 11 CAP 1 0 SCS 1 0 Set TBxCCR6 CCIFG Compare Latch TBxCL6 ACLK SMCLK TBxCLK INCLK Timer Clock Divider 1 2 4 8 ID IDEX Divider 1 8 2 2 3 2 2 2 2 2 2 3 Timer_B Introduction www ti com 666 SLAU367P October 2012 Revised April 2020 Submit Documentation...

Страница 667: ...figurable to operate as an 8 10 12 or 16 bit timer with the CNTL bits The maximum count value TBxR max for the selectable lengths is 0FFh 03FFh 0FFFh and 0FFFFh respectively Data written to the TBxR register in 8 10 and 12 bit mode is right justified with leading zeros 26 2 1 2 Clock Source Select and Divider The timer clock can be sourced from ACLK SMCLK or externally from TBxCLK or INCLK The clo...

Страница 668: ...erent from TBxR max counts The timer repeatedly counts up to the value of compare latch TBxCL0 which defines the period see Figure 26 2 The number of timer counts in the period is TBxCL0 1 When the timer value equals TBxCL0 the timer restarts counting from zero If up mode is selected when the timer value is greater than TBxCL0 the timer immediately restarts counting from zero Figure 26 2 Up Mode T...

Страница 669: ...Continuous Mode The TBIFG interrupt flag is set when the timer counts from TBxR max to zero Figure 26 5 shows the flag set cycle Figure 26 5 Continuous Mode Flag Setting 26 2 3 3 Use of Continuous Mode The continuous mode can be used to generate independent time intervals and output frequencies Each time an interval is completed an interrupt is generated The next time interval is added to the TBxC...

Страница 670: ... TBxCL0 TBxR max the counter operates as if it were configured for continuous mode It does not count down from TBxR max to zero Figure 26 7 Up Down Mode The count direction is latched This allows the timer to be stopped and then restarted in the same direction it was counting before it was stopped If this is not desired the TBCLR bit must be used to clear the direction Setting TBCLR also clears th...

Страница 671: ...In the example shown in Figure 26 9 the tdead is tdead ttimer TBxCL1 TBxCL3 Where tdead Time during which both outputs need to be inactive ttimer Cycle time of the timer clock TBxCLn Content of compare latch n The ability to simultaneously load grouped compare latches ensures the dead times Figure 26 9 Output Unit in Up Down Mode 26 2 4 Capture Compare Blocks Up to seven identical capture compare ...

Страница 672: ...on Setting the SCS bit synchronizes the capture with the next timer clock TI recommends setting the SCS bit to synchronize the capture signal with the timer clock see Figure 26 10 Figure 26 10 Capture Signal SCS 1 NOTE Changing Capture Inputs Changing capture inputs while in capture mode may cause unintended capture events To avoid this scenario capture inputs should only be changed when capture m...

Страница 673: ...n where n represents the specific capture compare latch Interrupt flag CCIFG is set Internal signal EQUn 1 EQUn affects the output according to the output mode 26 2 4 2 1 Compare Latch TBxCLn The TBxCCRn compare latch TBxCLn holds the data for the comparison to the timer value in compare mode TBxCLn is buffered by TBxCCRn The buffered compare latch gives the user control over when a compare period...

Страница 674: ...ion can be used to put all Timer_B outputs into a high impedance state When the TBOUTH pin function is selected for the pin corresponding PSEL bit is set and port configured as input and when the pin is pulled high all Timer_B outputs are in a high impedance state 26 2 5 1 Output Modes The output modes are defined by the OUTMOD bits and are described in Table 26 4 The OUTn signal is changed with t...

Страница 675: ...ts www ti com Timer_B Operation 675 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Timer_B 26 2 5 1 1 Output Example Timer in Up Mode The OUTn signal is changed when the timer counts up to the TBxCLn value and rolls from TBxCL0 to zero depending on the output mode An example is shown in Figure 26 12 using TBxCL0 and TBxCL1 ...

Страница 676: ... Timer_B Operation www ti com 676 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Timer_B 26 2 5 1 2 Output Example Timer in Continuous Mode The OUTn signal is changed when the timer reaches the TBxCLn and TBxCL0 values depending on the output mode An example is shown in Figure 26 13 using TBxCL0 and TBxCL1 Figure 26 13 Outp...

Страница 677: ... OUTn signal changes when the timer equals TBxCLn in either count direction and when the timer equals TBxCL0 depending on the output mode An example is shown in Figure 26 14 using TBxCL0 and TBxCL3 Figure 26 14 Output Example Timer in Up Down Mode NOTE Switching between output modes When switching between output modes one of the OUTMOD bits should remain set during the transition unless switching ...

Страница 678: ...o determine which flag requested an interrupt The highest priority enabled interrupt excluding TBxCCR0 CCIFG generates a number in the TBxIV register see register description This number can be evaluated or added to the program counter to automatically enter the appropriate software routine Disabled Timer_B interrupts do not affect the TBxIV value Any access read or write of the TBxIV register aut...

Страница 679: ...G_1_HND Vector 2 TB0CCR1 2 JMP CCIFG_2_HND Vector 4 TB0CCR2 2 JMP CCIFG_3_HND Vector 6 TB0CCR3 2 JMP CCIFG_4_HND Vector 8 TB0CCR4 2 JMP CCIFG_5_HND Vector 10 TB0CCR5 2 JMP CCIFG_6_HND Vector 12 TB0CCR6 2 TB0IFG_HND Vector 14 TB0IFG Flag Task starts here RETI 5 CCIFG_6_HND Vector 12 TB0CCR6 Task starts here RETI Back to main program 5 CCIFG_5_HND Vector 10 TB0CCR5 Task starts here RETI Back to main...

Страница 680: ...rd 0000h Section 26 3 3 0Ah TBxCCTL4 Timer_B Capture Compare Control 4 Read write Word 0000h Section 26 3 3 0Ch TBxCCTL5 Timer_B Capture Compare Control 5 Read write Word 0000h Section 26 3 3 0Eh TBxCCTL6 Timer_B Capture Compare Control 6 Read write Word 0000h Section 26 3 3 10h TBxR Timer_B Counter Read write Word 0000h Section 26 3 2 12h TBxCCR0 Timer_B Capture Compare 0 Read write Word 0000h Se...

Страница 681: ...ent 11b TBxCL0 TBxCL1 TBxCL2 TBxCL3 TBxCL4 TBxCL5 TBxCL6 TBxCCR1 CLLD bits control the update 12 11 CNTL RW 0h Counter length 00b 16 bit TBxR max 0FFFFh 01b 12 bit TBxR max 0FFFh 10b 10 bit TBxR max 03FFh 11b 8 bit TBxR max 0FFh 10 Reserved R 0h Reserved Always reads as 0 9 8 TBSSEL RW 0h Timer_B clock source select 00b TBxCLK 01b ACLK 10b SMCLK 11b INCLK 7 6 ID RW 0h Input divider These bits alon...

Страница 682: ... April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Timer_B Table 26 6 TBxCTL Register Description continued Bit Field Type Reset Description 0 TBIFG RW 0h Timer_B interrupt flag 0b No interrupt pending 1b Interrupt pending ...

Страница 683: ... Timer_B 26 3 2 TBxR Register Timer_B x Counter Register Figure 26 17 TBxR Register 15 14 13 12 11 10 9 8 TBxR rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 TBxR rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 26 7 TBxR Register Description Bit Field Type Reset Description 15 0 TBxR RW 0h Timer_B register The TBxR register is the count of Timer_B ...

Страница 684: ...CCIxB 10b GND 11b VCC 11 SCS RW 0h Synchronize capture source This bit is used to synchronize the capture input signal with the timer clock 0b Asynchronous capture 1b Synchronous capture 10 9 CLLD RW 0h Compare latch load These bits select the compare latch load event 00b TBxCLn loads on write to TBxCCRn 01b TBxCLn loads when TBxR counts to 0 10b TBxCLn loads when TBxR counts to 0 up or continuous...

Страница 685: ...ued Bit Field Type Reset Description 2 OUT RW 0h Output For output mode 0 this bit directly controls the state of the output 0b Output low 1b Output high 1 COV RW 0h Capture overflow This bit indicates a capture overflow occurred COV must be reset with software 0b No capture overflow occurred 1b Capture overflow occurred 0 CCIFG RW 0h Capture compare interrupt flag 0b No interrupt pending 1b Inter...

Страница 686: ...14 13 12 11 10 9 8 TBxCCRn rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 TBxCCRn rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 26 9 TBxCCRn Register Description Bit Field Type Reset Description 15 0 TBxCCRn RW 0h Timer_B capture compare register Compare mode TBxCCRn holds the data for the comparison to the timer value in the Timer_B Register TBR Capture mode The Timer_B Register TBR is c...

Страница 687: ...e Reset Description 15 0 TBIV R 0h Timer_B interrupt vector value 00h No interrupt pending 02h Interrupt Source Capture compare 1 Interrupt Flag TBxCCR1 CCIFG Interrupt Priority Highest 04h Interrupt Source Capture compare 2 Interrupt Flag TBxCCR2 CCIFG 06h Interrupt Source Capture compare 3 Interrupt Flag TBxCCR3 CCIFG 08h Interrupt Source Capture compare 4 Interrupt Flag TBxCCR4 CCIFG 0Ah Interr...

Страница 688: ... divider logic Figure 26 21 TBxEX0 Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved TBIDEX 1 r0 r0 r0 r0 r0 rw 0 rw 0 rw 0 Table 26 11 TBxEX0 Register Description Bit Field Type Reset Description 15 3 Reserved R 0h Reserved Always reads as 0 2 0 TBIDEX RW 0h Input divider expansion These bits along with the ID bits select the divider for the input clock 000b...

Страница 689: ...Programmable Alarms Yes Yes Password Protected Calendar Registers No Yes Input Clocks 32 kHz crystal oscillator 32 kHz crystal oscillator LPM3 5 Support Yes Yes Offset Calibration Register Yes Yes Temperature Compensation Register No Yes Frequency Adjustment Range 2 17 ppm 59 128 ppm 4 34 ppm 59 256 ppm 240 ppm 240 ppm 2 Frequency Adjustment Steps 2 17 ppm 4 34 ppm 1 ppm 1 ppm Temperature Compensa...

Страница 690: ...al time clock RTC_B module provides clock counters with calendar mode a flexible programmable alarm and calibration Note that the RTC_B supports only calendar mode and not counter mode The RTC_B also support operation in LPM3 5 See the device specific data sheet for the supported features This chapter describes the RTC_B module Topic Page 28 1 Real Time Clock RTC_B Introduction 691 28 2 RTC_B Oper...

Страница 691: ...urs day of week day of month month and year including leap year correction Note that only the calendar mode is supported by RTC_B the counter mode that is available in some other RTC modules is not supported Interrupt capability Selectable BCD or binary format Programmable alarms Calibration logic for time offset correction Operation in LPM3 5 The RTC_B block diagram for devices supporting LPM3 5 ...

Страница 692: ...0 011 010 001 000 3 RT0IP RTCHOLD Keepout Logic Set_RTCRDYIFG Calibration Logic 5 RTCCALS RTCCAL Q0 Q1 Q2 Q3 Q4 Q5 Q6 Q7 111 hour changed midnight noon RTCHOUR RTCMIN RTCSEC 110 101 100 011 010 001 000 111 from 32kHz Crystal Osc Real Time Clock RTC_B Introduction www ti com 692 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated...

Страница 693: ...15 00 01 15 00 02 15 00 etc This is possible by setting RTCAMIN to 15 By setting the AE bit of the RTCAMIN and clearing all other AE bits of the alarm registers the alarm is enabled When enabled the RTCAIFG is set when the count transitions from 00 14 59 to 00 15 00 01 14 59 to 01 15 00 02 14 59 to 02 15 00 and so on Example 2 A user wishes to set an alarm every day at 04 00 00 This is possible by...

Страница 694: ... transition The RTCRDYIFG flag is reset automatically when the interrupt is serviced or it can be reset with software NOTE Reading or writing real time clock registers When the counter clock is asynchronous to the CPU clock any read from any RTCSEC RTCMIN RTCHOUR RTCDOW RTCDAY RTCMON or RTCYEAR register while the RTCRDY is reset may result in invalid data being read To safely read the counting reg...

Страница 695: ... 2 Hz 1 Hz or 0 5 Hz are possible Setting the RT1PSIE bit enables the interrupt NOTE Changing RT0IP or RT1IP Changing the settings of the interrupt interval bits RT0IP or RT1IP while the corresponding prescaler is running or is stopped in a non zero state can result in setting the corresponding interrupt flags The RTCOFIFG bit flags a failure of the 32 kHz crystal oscillator Its main purpose is to...

Страница 696: ... causes either 256 LF crystal clock cycles to be added every 60 minutes or 512 LF crystal clock cycles to be subtracted every 60 minutes giving a frequency adjustment of approximately 2 ppm or 4 ppm respectively To calibrate the frequency the RTCCLK output signal is available at a pin RTCCALF bits can be used to select the frequency rate of the output signal either no signal 512 Hz 256 Hz or 1 Hz ...

Страница 697: ...sters and clearing LOCKLPM5 the interrupts can be serviced as usual The detailed flow is as follows 1 Set all I Os to general purpose I Os and configure as needed Optionally configure input interrupt pins for wake up Configure RTC_B interrupts for wake up set RTCTEVIE RTCAIE RT1PSIE or RTCOFIE If the alarm interrupt is also used as wake up event the alarm registers must be configured as needed 2 E...

Страница 698: ...2h RTCCTL2 Real Time Clock Control 2 Read write Byte 00h retained or RTCCTL23_L 03h RTCCTL3 Real Time Clock Control 3 Read write Byte 00h retained or RTCCTL23_H 08h RTCPS0CTL Real Time Prescale Timer 0 Control Read write Word 0000h not retained 08h RTCPS0CTLL Read write Byte 00h not retained or RTCPS0CTL_L 09h RTCPS0CTLH Read write Byte 00h not retained or RTCPS0CTL_H 0Ah RTCPS1CTL Real Time Presc...

Страница 699: ...RTCYEAR Real Time Clock Year 1 Read write Word undefined retained 18h RTCAMINHR Real Time Clock Minutes Hour Alarm Read write Word undefined retained 18h RTCAMIN Real Time Clock Minutes Alarm Read write Byte undefined retained or RTCAMINHR_L 19h RTCAHOUR Real Time Clock Hours Alarm Read write Byte undefined retained or RTCAMINHR_H 1Ah RTCADOWDAY Real Time Clock Day of Week Day of Month Alarm Read ...

Страница 700: ... can be used as LPMx 5 wake up event 0b Interrupt not enabled 1b Interrupt enabled LPMx 5 wake up enabled 5 RTCAIE RW 0h Real time clock alarm interrupt enable In modules supporting LPMx 5 this interrupt can be used as LPMx 5 wake up event 0b Interrupt not enabled 1b Interrupt enabled LPMx 5 wake up enabled 4 RTCRDYIE RW 0h Real time clock ready interrupt enable 0b Interrupt not enabled 1b Interru...

Страница 701: ...CTL1 Register Description Bit Field Type Reset Description 7 RTCBCD RW 0h Real time clock BCD select Selects BCD counting for real time clock 0b Binary hexadecimal code selected 1b BCD Binary coded decimal BCD code selected 6 RTCHOLD RW 1h Real time clock hold 0b Real time clock is operational 1b The calendar is stopped as well as the prescale counters RT0PS and RT1PS 5 Reserved R 1h Reserved Alwa...

Страница 702: ...6 Reserved R 0h Reserved Always read as 0 5 0 RTCCALx RW 0h Real time clock calibration Each LSB represents approximately 4 ppm RTCCALS 1 or a 2 ppm RTCCALS 0 adjustment in frequency 28 3 4 RTCCTL3 Register Real Time Clock Control 3 Register Figure 28 5 RTCCTL3 Register 7 6 5 4 3 2 1 0 Reserved RTCCALFx r0 r0 r0 r0 r0 r0 rw 0 rw 0 Table 28 5 RTCCTL3 Register Description Bit Field Type Reset Descri...

Страница 703: ...ster Description Bit Field Type Reset Description 7 6 0 R 0h Always reads as 0 5 0 Seconds RW undefined Seconds Valid values are 0 to 59 28 3 6 RTCSEC Register BCD Format Real Time Clock Seconds Register BCD Format Figure 28 7 RTCSEC Register 7 6 5 4 3 2 1 0 0 Seconds high digit Seconds low digit r 0 rw rw rw rw rw rw rw Table 28 7 RTCSEC Register Description Bit Field Type Reset Description 7 0 R...

Страница 704: ...ster Description Bit Field Type Reset Description 7 6 0 R 0h Always reads as 0 5 0 Minutes RW undefined Minutes Valid values are 0 to 59 28 3 8 RTCMIN Register BCD Format Real Time Clock Minutes Register BCD Format Figure 28 9 RTCMIN Register 7 6 5 4 3 2 1 0 0 Minutes high digit Minutes low digit r 0 rw rw rw rw rw rw rw Table 28 9 RTCMIN Register Description Bit Field Type Reset Description 7 0 R...

Страница 705: ... Register Description Bit Field Type Reset Description 7 5 0 R 0h Always reads as 0 4 0 Hours RW undefined Hours Valid values are 0 to 23 28 3 10 RTCHOUR Register BCD Format Real Time Clock Hours Register BCD Format Figure 28 11 RTCHOUR Register 7 6 5 4 3 2 1 0 0 0 Hours high digit Hours low digit r 0 r 0 rw rw rw rw rw rw Table 28 11 RTCHOUR Register Description Bit Field Type Reset Description 7...

Страница 706: ... Register Hexadecimal Format Figure 28 13 RTCDAY Register 7 6 5 4 3 2 1 0 0 0 0 Day of month r 0 r 0 r 0 rw rw rw rw rw Table 28 13 RTCDAY Register Description Bit Field Type Reset Description 7 5 0 R 0h Always reads as 0 4 0 Day of month RW undefined Day of month Valid values are 1 to 31 28 3 13 RTCDAY Register BCD Format Real Time Clock Day of Month Register BCD Format Figure 28 14 RTCDAY Regist...

Страница 707: ... RTCMON Register Description Bit Field Type Reset Description 7 4 0 R 0h Always reads as 0 3 0 Month RW undefined Month Valid values are 1 to 12 28 3 15 RTCMON Register BCD Format Real Time Clock Month Register Figure 28 16 RTCMON Register 7 6 5 4 3 2 1 0 0 0 0 Month high digit Month low digit r 0 r 0 r 0 rw rw rw rw rw Table 28 16 RTCMON Register Description Bit Field Type Reset Description 7 5 0...

Страница 708: ... Valid values of Year are 0 to 4095 7 0 Year low byte RW undefined Year low byte Valid values of Year are 0 to 4095 28 3 17 RTCYEAR Register BCD Format Real Time Clock Year Register BCD Format Figure 28 18 RTCYEAR Register 15 14 13 12 11 10 9 8 0 Century high digit Century low digit r 0 rw rw rw rw rw rw rw 7 6 5 4 3 2 1 0 Decade Year lowest digit rw rw rw rw rw rw rw rw Table 28 18 RTCYEAR Regist...

Страница 709: ...is alarm register is disabled 1b This alarm register is enabled 6 0 R 0h Always reads as 0 5 0 Minutes RW undefined Minutes Valid values are 0 to 59 28 3 19 RTCAMIN Register BCD Format Real Time Clock Minutes Alarm Register BCD Format Figure 28 20 RTCAMIN Register 7 6 5 4 3 2 1 0 AE Minutes high digit Minutes low digit rw rw rw rw rw rw rw rw Table 28 20 RTCAMIN Register Description Bit Field Type...

Страница 710: ...m register is disabled 1b This alarm register is enabled 6 5 0 R 0h Always reads as 0 4 0 Hours RW undefined Hours Valid values are 0 to 23 28 3 21 RTCAHOUR Register BCD Format Real Time Clock Hours Alarm Register BCD Format Figure 28 22 RTCAHOUR Register 7 6 5 4 3 2 1 0 AE 0 Hours high digit Hours low digit rw r 0 rw rw rw rw rw rw Table 28 22 RTCAHOUR Register Description Bit Field Type Reset De...

Страница 711: ...al Time Clock Day of Week Alarm Register Figure 28 23 RTCADOW Register 7 6 5 4 3 2 1 0 AE 0 0 0 0 Day of week rw r 0 r 0 r 0 r 0 rw rw rw Table 28 23 RTCADOW Register Description Bit Field Type Reset Description 7 AE RW undefined Alarm enable 0b This alarm register is disabled 1b This alarm register is enabled 6 3 0 R 0h Always reads as 0 2 0 Day of week RW undefined Day of week Valid values are 0...

Страница 712: ... This alarm register is enabled 6 5 0 R 0h Always reads as 0 4 0 Day of month RW undefined Day of month Valid values are 1 to 31 28 3 24 RTCADAY Register BCD Format Real Time Clock Day of Month Alarm Register BCD Format Figure 28 25 RTCADAY Register 7 6 5 4 3 2 1 0 AE 0 Day of month high digit Day of month low digit rw r 0 rw rw rw rw rw rw Table 28 25 RTCADAY Register Description Bit Field Type R...

Страница 713: ...26 RTCPS0CTL Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved RT0IPx 1 RT0PSIE RT0PSIFG r0 r0 r0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 28 26 RTCPS0CTL Register Description Bit Field Type Reset Description 15 5 Reserved R 0h Reserved Always reads as 0 4 2 RT0IPx RW 0h Prescale timer 0 interrupt interval 000b Divide by 2 001b Divide by 4 010b Divide by 8 011b Divide ...

Страница 714: ...ed r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved RT1IPx 1 RT1PSIE 1 RT1PSIFG r0 r0 r0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 28 27 RTCPS1CTL Register Description Bit Field Type Reset Description 15 5 Reserved R 0h Reserved Always reads as 0 4 2 RT1IPx RW 0h Prescale timer 1 interrupt interval 000b Divide by 2 001b Divide by 4 010b Divide by 8 011b Divide by 16 100b Divide by 32 101b Divide by 64 110b D...

Страница 715: ... RTCPS0 Register 7 6 5 4 3 2 1 0 RT0PS rw rw rw rw rw rw rw rw Table 28 28 RTCPS0 Register Description Bit Field Type Reset Description 7 0 RT0PS RW undefined Prescale timer 0 counter value 28 3 28 RTCPS1 Register Real Time Clock Prescale Timer 1 Counter Register Figure 28 29 RTCPS1 Register 7 6 5 4 3 2 1 0 RT1PS rw rw rw rw rw rw rw rw Table 28 29 RTCPS1 Register Description Bit Field Type Reset ...

Страница 716: ...8 30 RTCIV Register Description Bit Field Type Reset Description 15 0 RTCIVx R 0h Real time clock interrupt vector value 00h No interrupt pending 02h Interrupt Source RTC ready Interrupt Flag RTCRDYIFG Interrupt Priority Highest 04h Interrupt Source RTC interval timer Interrupt Flag RTCTEVIFG 06h Interrupt Source RTC user alarm Interrupt Flag RTCAIFG 08h Interrupt Source RTC prescaler 0 Interrupt ...

Страница 717: ...BCD Register Description Bit Field Type Reset Description 15 0 BIN2BCDx RW 0h Read 16 bit BCD conversion of previously written 12 bit binary number Write 12 bit binary number to be converted 28 3 31 BCD2BIN Register BCD to Binary Conversion Register Figure 28 32 BCD2BIN Register 15 14 13 12 11 10 9 8 BCD2BINx rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 BCD2BINx rw 0 rw 0 rw 0 rw 0 rw 0...

Страница 718: ...C RTC_C The Real Time Clock C RTC_C module provides clock counters with calendar mode a flexible programmable alarm offset calibration and a provision for temperature compensation The RTC_C also supports operation in LPM3 5 This chapter describes the RTC_C module Topic Page 29 1 Real Time Clock RTC_C Introduction 719 29 2 RTC_C Operation 721 29 3 RTC_C Operation Device Dependent Features 729 29 4 ...

Страница 719: ...ility Selectable BCD or binary format Programmable alarms Real time clock calibration for crystal offset error Real time clock compensation for crystal temperature drift Operation in LPM3 5 The RTC_C module can provide the following device dependent features Refer to the device specific data sheet to determine if these features are available in a particular device General purpose counter mode see ...

Страница 720: ...t_RTCRDYIFG Q0 Q1 Q2 Q3 Q4 Q5 Q6 Q7 111 hour changed midnight noon RTCHOUR RTCMIN RTCSEC 110 101 100 011 010 001 000 111 RTCOCALS RTCOCAL EN Calibration Logic 8 RTCTCMPS RTCTCMP 8 RTCHOLD From 32 kHz Crystal Oscillator Copyright 2016 Texas Instruments Incorporated Real Time Clock RTC_C Introduction www ti com 720 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012...

Страница 721: ...rm that can be programmed based on the settings contained in the alarm registers for minutes hours day of week and day of month Each alarm register contains an alarm enable AE bit that can be used to enable the respective alarm register By setting AE bits of the various alarm registers a variety of alarm events can be generated Example 1 A user wishes to set an alarm every hour at 15 minutes past ...

Страница 722: ...ule Some predefined registers of RTC_C are key protected for write access The control registers clock registers calendar register prescale timer registers and offset error calibration registers are protected RTC_C alarm function registers prescale timer control registers interrupt vector register and temperature compensation registers are not protected RTC_C registers that are not protected can be...

Страница 723: ...multiple times and a majority vote taken in software to determine the correct reading Any write to any counting register takes effect immediately However the clock is stopped during the write In addition RT0PS and RT1PS registers are reset This could result in losing up to 1 second during a write Writing of data outside the legal ranges or invalid time stamp combinations results in unpredictable b...

Страница 724: ... and RTC_C is accessible only when SVSH is enabled 29 2 6 1 RTCIV Software Example The following software example shows the recommended use of RTCIV and the handling overhead The RTCIV value is added to the PC to automatically jump to the appropriate routine The numbers at the right margin show the necessary CPU cycles for each instruction The software overhead for different interrupt sources incl...

Страница 725: ...ly 240 ppm Software must make sure to write legal values into this register A read from RTCOCAL always returns the value that was written by software Real time clock offset error calibration is inactive when RTC_C is not enabled RTCHOLD 0 or when RTCOCALx bits are zero RTCOCAL should only be written when RTCHOLD 1 Writing RTCOCAL resets temperature compensation to zero In RTC_C the offset error ca...

Страница 726: ...libration value and the resulting value is taken into account from next calibration cycle onwards The ongoing calibration cycle is not affected by writes into the RTCTCMP register The maximum frequency error that can be corrected to account for both offset error and temperature variation is 240 ppm This means the sign addition of offset error value and temperature compensation value should not exc...

Страница 727: ...ay wish to perform temperature measurement once every few seconds or once every minute or once in several minutes Writing to RTCTCMP register for temperature compensation is effective always once in one minute This means that if the user performs temperature measurement every minute and updates RTCTCMP register with the frequency error compensation would immediately work fine But if software perfo...

Страница 728: ...C interrupts for wake up set RTCTEVIE RTCAIE RT1PSIE or RTCOFIE If the alarm interrupt is also used as wake up event the alarm registers must be configured as needed 2 Enter LPM3 5 with LPM3 5 entry sequence bic RTCHOLD RTCCTL13 bis PMMKEY REGOFF PMMCTL0 bis LPM4 SR 3 LOCKLPM5 is automatically set by hardware upon entering LPM3 5 the core voltage regulator is disabled and all clocks are disabled e...

Страница 729: ...r 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Real Time Clock C RTC_C 29 3 RTC_C Operation Device Dependent Features 29 3 1 Counter Mode NOTE This feature is available only on selected devices See the device specific data sheet to determine if this feature is available The RTC_C module can be configured as a real time clock with calendar...

Страница 730: ...utput can also be used as a clock source input to the 32 bit counter Four individual 8 bit counters are cascaded to provide the 32 bit counter This provides 8 bit 16 bit 24 bit or 32 bit overflow intervals of the counter clock The RTCTEV bits select the respective trigger event An RTCTEV event can trigger an interrupt by setting the RTCTEVIE bit Each counter RTCNT1 through RTCNT4 is individually a...

Страница 731: ...he interrupt RT1PSIFG can be used to generate interrupt intervals selectable by the RT1IP bits In counter mode RT1PS is sourced with low frequency oscillator clock or the output of RT0PS so divide ratios of 2 4 8 16 32 64 128 and 256 of the respective clock source are possible Setting the RT1PSIE bit enables the interrupt In Counter Mode the RTC_C module provides for an interval timer that sources...

Страница 732: ... cleared by the user The CAPES bit in the RTCCAPxCTL register sets the event edge for the corresponding RTCCAPx pin Bit 0 CAPEV flag is set with a low to high transition Bit 1 CAPEV flag is set with a high to low transition NOTE Writing to CAPESx Writing to CAPES can result in setting the corresponding interrupt flags CAPESx RTCCAPx RTCCAPIFG 0 1 0 May be set 0 1 1 Unchanged 1 0 0 Unchanged 1 0 1 ...

Страница 733: ...ion Interrupts With the event or tamper detection feature one additional interrupt sources is available RTCCAPIFG This flag is prioritized and combined with the other interrupt flags to source a single interrupt vector The interrupt vector register RTCIV is used to determine which flag requested an interrupt The RTCCAPIFG bit flags the occurrence of a tamper event The exact source of the interrupt...

Страница 734: ... the upper byte of the register bits 8 through 15 1 Some bits in this register are retained See the register description to determine which bits are retained Table 29 2 RTC_C Registers Offset Acronym Register Name Type Access Reset Key Protected LPM3 5 Retention 00h RTCCTL0 Real Time Clock Control 0 Read write Word 9600h yes not retained 1 00h RTCCTL0_L Real Time Clock Control 0 Low Read write Byt...

Страница 735: ...OUR Real Time Clock Hour Read write Byte undefined yes retained or RTCTIM1_L 13h RTCDOW Real Time Clock Day of Week Read write Byte undefined yes retained or RTCTIM1_H 14h RTCDATE Real Time Clock Date Read write Word undefined yes retained 14h RTCDAY Real Time Clock Day of Month Read write Byte undefined yes retained or RTCDATE_L 15h RTCMON Real Time Clock Month Read write Byte undefined yes retai...

Страница 736: ...al Time Clock Months Backup Register 0 Read write Byte 00h yes retained 36h RTCYEARBAK0 Real Time Clock year Backup Register 0 Read write Word 00h yes retained 38h RTCSECBAK1 Real Time Clock Seconds Backup Register 1 Read write Byte 00h yes retained 39h RTCMINBAK1 Real Time Clock Minutes Backup Register 1 Read write Byte 00h yes retained 3Ah RTCHOURBAK1 Real Time Clock Hours Backup Register 1 Read...

Страница 737: ...errupt can be used as LPM3 5 wake up event 0b Interrupt not enabled 1b Interrupt enabled LPM3 5 wake up enabled 5 RTCAIE RW 0h Real time clock alarm interrupt enable In modules supporting LPM3 5 this interrupt can be used as LPM3 5 wake up event 0b Interrupt not enabled 1b Interrupt enabled LPM3 5 wake up enabled 4 RTCRDYIE RW 0h Real time clock ready interrupt enable 0b Interrupt not enabled 1b I...

Страница 738: ...r Real Time Clock Control 0 High Register Figure 29 5 RTCCTL0_H Register 7 6 5 4 3 2 1 0 RTCKEY rw 1 rw 0 rw 0 rw 1 rw 0 rw 1 rw 1 rw 0 Table 29 6 RTCCTL0_H Register Description Bit Field Type Reset Description 7 0 RTCKEY RW 96h Real time clock key This register should be written with A5h to unlock RTC_C A write with a value other than A5h locks the module A read from this register always returns ...

Страница 739: ...r is stopped as well as the prescale counters RT0PS and RT1PS RT0PSHOLD and RT1PSHOLD are don t care 5 RTCMODE RW 1h Real time clock mode In RTC_C modules without counter mode support this bit is read only and always reads 1 0b 32 bit counter mode 1b Calendar mode Switching between counter and calendar mode does not reset the real time clock counter registers These registers must be configured by ...

Страница 740: ...he RTCCALF bits are don t care 00b No frequency output to RTCCLK pin 01b 512 Hz 10b 256 Hz 11b 1 Hz 29 4 5 RTCOCAL Register Real Time Clock Offset Calibration Register 1 These bits are not reset on POR Figure 29 8 RTCOCAL Register 15 14 13 12 11 10 9 8 RTCOCALS 1 Reserved rw 0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 RTCOCALx 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table 29 9 RTCOCAL Register Descri...

Страница 741: ...the sign of temperature compensation 1 0b Down calibration Frequency adjusted down 1b Up calibration Frequency adjusted up 14 RTCTCRDY R 1h Real time clock temperature compensation ready This is a read only bit that indicates when the RTCTCMPx can be written Write to RTCTCMPx should be avoided when RTCTCRDY is reset 13 RTCTCOK R 0h Real time clock temperature compensation write OK This is a read o...

Страница 742: ...r 7 6 5 4 3 2 1 0 RTCNT2 rw rw rw rw rw rw rw rw Table 29 12 RTCNT2 Register Description Bit Field Type Reset Description 7 0 RTCNT2 RW undefined The RTCNT2 register is the count of RTCNT2 29 4 9 RTCNT3 Register Real Time Clock Counter 3 Register Counter Mode Figure 29 12 RTCNT3 Register 7 6 5 4 3 2 1 0 RTCNT3 rw rw rw rw rw rw rw rw Table 29 13 RTCNT3 Register Description Bit Field Type Reset Des...

Страница 743: ... rw rw rw Table 29 15 RTCSEC Register Description Bit Field Type Reset Description 7 6 0 R 0h Always 0 5 0 Seconds RW undefined Seconds 0 to 59 29 4 12 RTCSEC Register Calendar Mode With BCD Format Real Time Clock Seconds Register Calendar Mode With BCD Format Figure 29 15 RTCSEC Register 7 6 5 4 3 2 1 0 0 Seconds high digit Seconds low digit r 0 rw rw rw rw rw rw rw Table 29 16 RTCSEC Register De...

Страница 744: ... rw rw rw Table 29 17 RTCMIN Register Description Bit Field Type Reset Description 7 6 0 R 0h Always 0 5 0 Minutes RW undefined Minutes 0 to 59 29 4 14 RTCMIN Register Calendar Mode With BCD Format Real Time Clock Minutes Register Calendar Mode With BCD Format Figure 29 17 RTCMIN Register 7 6 5 4 3 2 1 0 0 Minutes high digit Minutes low digit r 0 rw rw rw rw rw rw rw Table 29 18 RTCMIN Register De...

Страница 745: ...rw rw rw rw rw Table 29 19 RTCHOUR Register Description Bit Field Type Reset Description 7 5 0 R 0h Always 0 4 0 Hours RW undefined Hours 0 to 23 29 4 16 RTCHOUR Register Calendar Mode With BCD Format Real Time Clock Hours Register Calendar Mode With BCD Format Figure 29 19 RTCHOUR Register 7 6 5 4 3 2 1 0 0 Hours high digit Hours low digit r 0 r 0 rw rw rw rw rw rw Table 29 20 RTCHOUR Register De...

Страница 746: ...ock Day of Month Register Calendar Mode With Hexadecimal Format Figure 29 21 RTCDAY Register 7 6 5 4 3 2 1 0 0 Day of month r 0 r 0 r 0 rw rw rw rw rw Table 29 22 RTCDAY Register Description Bit Field Type Reset Description 7 5 0 R 0h Always 0 4 0 Day of month RW undefined Day of month 1 to 28 29 30 31 29 4 19 RTCDAY Register Calendar Mode With BCD Format Real Time Clock Day of Month Register Cale...

Страница 747: ... r 0 rw rw rw rw Table 29 24 RTCMON Register Description Bit Field Type Reset Description 7 4 0 R 0h Always 0 3 0 Month RW undefined Month 1 to 12 29 4 21 RTCMON Register Calendar Mode With BCD Format Real Time Clock Month Register Calendar Mode With BCD Format Figure 29 24 RTCMON Register 7 6 5 4 3 2 1 0 0 Month high digit Month low digit r 0 r 0 r 0 rw rw rw rw rw Table 29 25 RTCMON Register Des...

Страница 748: ...te RW undefined Year high byte Valid values for Year are 0 to 4095 7 0 Year low byte RW undefined Year low byte Valid values for Year are 0 to 4095 29 4 23 RTCYEAR Register Calendar Mode With BCD Format Real Time Clock Year Low Byte Register Calendar Mode With BCD Format Figure 29 26 RTCYEAR Register 15 14 13 12 11 10 9 8 0 Century high digit Century low digit r 0 rw rw rw rw rw rw rw 7 6 5 4 3 2 ...

Страница 749: ...W undefined Alarm enable 0b This alarm register is disabled 1b This alarm register is enabled 6 0 R 0h Always 0 5 0 Minutes RW undefined Minutes 0 to 59 29 4 25 RTCAMIN Register Calendar Mode With BCD Format Real Time Clock Minutes Alarm Register Calendar Mode With BCD Format Figure 29 28 RTCAMIN Register 7 6 5 4 3 2 1 0 AE Minutes high digit Minutes low digit rw rw rw rw rw rw rw rw Table 29 29 R...

Страница 750: ...e 0b This alarm register is disabled 1b This alarm register is enabled 6 5 0 R 0h Always 0 4 0 Hours RW undefined Hours 0 to 23 29 4 27 RTCAHOUR Register Calendar Mode With BCD Format Real Time Clock Hours Alarm Register Calendar Mode With BCD Format Figure 29 30 RTCAHOUR Register 7 6 5 4 3 2 1 0 AE 0 Hours high digit Hours low digit rw r 0 rw rw rw rw rw rw Table 29 31 RTCAHOUR Register Descripti...

Страница 751: ...Calendar Mode Real Time Clock Day of Week Alarm Register Calendar Mode Figure 29 31 RTCADOW Register 7 6 5 4 3 2 1 0 AE 0 Day of week rw r 0 r 0 r 0 r 0 rw rw rw Table 29 32 RTCADOW Register Description Bit Field Type Reset Description 7 AE RW undefined Alarm enable 0b This alarm register is disabled 1b This alarm register is enabled 6 3 0 R 0h Always 0 2 0 Day of week RW undefined Day of week 0 t...

Страница 752: ...alarm register is disabled 1b This alarm register is enabled 6 5 0 R 0h Always 0 4 0 Day of month RW undefined Day of month 1 to 28 29 30 31 29 4 30 RTCADAY Register Calendar Mode With BCD Format Real Time Clock Day of Month Alarm Register Calendar Mode With BCD Format Figure 29 33 RTCADAY Register 7 6 5 4 3 2 1 0 AE 0 Day of month high digit Day of month low digit rw r 0 rw rw rw rw rw rw Table 2...

Страница 753: ... clock divide These bits control the divide ratio of the RT0PS counter In real time clock calendar mode these bits are don t care for RT0PS and RT1PS RT0PS clock output is automatically set to 256 RT1PS clock output is automatically set to 128 000b Divide by 2 001b Divide by 4 010b Divide by 8 011b Divide by 16 100b Divide by 32 101b Divide by 64 110b Divide by 128 111b Divide by 256 10 9 Reserved...

Страница 754: ...atically set to the output of RT0PS 00b 32 kHz crystal oscillator clock 01b 32 kHz crystal oscillator clock 10b Output from RT0PS 11b Output from RT0PS 13 11 RT1PSDIVx RW 0h Prescale timer 1 clock divide These bits control the divide ratio of the RT0PS counter In real time clock calendar mode these bits are don t care for RT0PS and RT1PS RT0PS clock output is automatically set to 256 RT1PS clock o...

Страница 755: ...yright 2012 2020 Texas Instruments Incorporated Real Time Clock C RTC_C Table 29 36 RTCPS1CTL Register Description continued Bit Field Type Reset Description 0 RT1PSIFG RW 0h Prescale timer 1 interrupt flag This interrupt can be used as LPMx 5 wake up event 0b No time event occurred 1b Time event occurred ...

Страница 756: ... RTCPS0 Register 7 6 5 4 3 2 1 0 RT0PS rw rw rw rw rw rw rw rw Table 29 37 RTCPS0 Register Description Bit Field Type Reset Description 7 0 RT0PS RW undefined Prescale timer 0 counter value 29 4 34 RTCPS1 Register Real Time Clock Prescale Timer 1 Counter Register Figure 29 37 RTCPS1 Register 7 6 5 4 3 2 1 0 RT1PS rw rw rw rw rw rw rw rw Table 29 38 RTCPS1 Register Description Bit Field Type Reset ...

Страница 757: ...ready Interrupt Flag RTCRDYIFG 06h Interrupt Source RTC interval timer Interrupt Flag RTCTEVIFG 08h Interrupt Source RTC user alarm Interrupt Flag RTCAIFG 0Ah Interrupt Source RTC prescaler 0 Interrupt Flag RT0PSIFG 0Ch Interrupt Source RTC prescaler 1 Interrupt Flag RT1PSIFG 0Eh Reserved 10h Reserved Interrupt Priority Lowest With Event Tamper Detection implemented 00h No interrupt pending 02h In...

Страница 758: ...BCD Register Description Bit Field Type Reset Description 15 0 BIN2BCDx RW 0h Read 16 bit BCD conversion of previously written 12 bit binary number Write 12 bit binary number to be converted 29 4 37 BCD2BIN Register BCD to Binary Conversion Register Figure 29 40 BCD2BIN Register 15 14 13 12 11 10 9 8 BCD2BINx rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 BCD2BINx rw 0 rw 0 rw 0 rw 0 rw 0...

Страница 759: ...2 RTCSECBAKx Register Description Bit Field Type Reset Description 7 6 0 RW 0h Always 0 5 0 Seconds RW 0h Seconds Valid values are 0 to 59 29 4 39 RTCSECBAKx Register BCD Format Real Time Clock Seconds Backup Register BCD Format 1 These bits are not reset on POR Figure 29 42 RTCSECBAKx Register 7 6 5 4 3 2 1 0 0 Seconds high digit 1 Seconds low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table...

Страница 760: ...4 RTCMINBAKx Register Description Bit Field Type Reset Description 7 6 0 RW 0h Always 0 5 0 Minutes RW 0h Minutes Valid values are 0 to 59 29 4 41 RTCMINBAKx Register BCD Format Real Time Clock Minutes Backup Register BCD Format 1 These bits are not reset on POR Figure 29 44 RTCMINBAKx Register 7 6 5 4 3 2 1 0 0 Minutes high digit 1 Minutes low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table...

Страница 761: ... 29 46 RTCHOURBAKx Register Description Bit Field Type Reset Description 7 5 0 RW 0h Always 0 4 0 Hours RW 0h Hours Valid values are 0 to 23 29 4 43 RTCHOURBAKx Register BCD Format Real Time Clock Hours Backup Register BCD Format 1 These bits are not reset on POR Figure 29 46 RTCHOURBAKx Register 7 6 5 4 3 2 1 0 0 0 Hours high digit 1 Hours low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table...

Страница 762: ...er Description Bit Field Type Reset Description 7 5 0 RW 0h Always 0 4 0 Day of month RW 0h Day of month Valid values are 1 to 31 29 4 45 RTCDAYBAKx Register BCD Format Real Time Clock Day of Month Backup Register BCD Format 1 These bits are not reset on POR Figure 29 48 RTCDAYBAKx Register 7 6 5 4 3 2 1 0 0 0 Day of month high digit 1 Day of month low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw...

Страница 763: ...le 29 50 RTCMONBAKx Register Description Bit Field Type Reset Description 7 4 0 RW 0h Always 0 3 0 Month RW 0h Month Valid values are 1 to 12 29 4 47 RTCMONBAKx Register BCD Format Real Time Clock Month Backup Register BCD Format 1 These bits are not reset on POR Figure 29 50 RTCMONBAKx Register 7 6 5 4 3 2 1 0 0 0 Month high digit 1 Month low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Table ...

Страница 764: ... high byte Valid values of Year are 0 to 4095 7 0 Year low byte RW 0h Year low byte Valid values of Year are 0 to 4095 29 4 49 RTCYEARBAKx Register BCD Format Real Time Clock Year Low Byte Backup Register BCD Format 1 These bits are not reset on POR Figure 29 52 RTCYEARBAKx Register 15 14 13 12 11 10 9 8 0 Century high digit 1 Century low digit 1 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2...

Страница 765: ...amper detection with time stamp 0b Tamper detection with time stamp disabled 1b Tamper detection with time stamp enabled 29 4 51 RTCTCCTL1 Register Real Time Clock Time Capture Control Register 1 Figure 29 54 RTCTCCTL1 Register 7 6 5 4 3 2 1 0 Reserved RTCCAPIE RTCCAPIFG r 0 r 0 r 0 r 0 r 0 r 0 rw 0 rw 0 Table 29 55 RTCTCCTL1 Register Description Bit Field Type Reset Description 7 2 Reserved R 0h ...

Страница 766: ...lways reads as 0 6 OUT RW 0h RTCCAPx output 0b Output low 1b Output high 5 DIR RW 0h RTCCAPx pin direction 0b RTCCAPx pin configured as input 1b RTCCAPx pin configured as output 4 IN R 0h RTCCAPx input The external input on RTCCAPx pin can be read by this bit 0b Input is low 1b Input is high 3 REN RW 0h RTCCAPx pin pullup or pulldown resistor enable When respective pin is configured as input setti...

Страница 767: ...Universal Serial Communication Interface eUSCI UART Mode The enhanced universal serial communication interface A eUSCI_A supports multiple serial communication modes with one hardware module This chapter discusses the operation of the asynchronous UART mode Topic Page 30 1 Enhanced Universal Serial Communication Interface A eUSCI_A Overview 768 30 2 eUSCI_A Introduction UART Mode 768 30 3 eUSCI_A ...

Страница 768: ...nd UCAxTXD UART mode is selected when the UCSYNC bit is cleared UART mode features include 7 bit or 8 bit data with odd even or no parity Independent transmit and receive shift registers Separate transmit and receive buffer registers LSB first or MSB first data transmit and receive Built in idle line and address bit communication protocols for multiprocessor systems Receiver start edge detection f...

Страница 769: ...DA Decoder UCIRRXFE UCIRRXFLx 6 Transmit Buffer UCAxTXBUF Transmit State Machine UCTXADDR UCTXBRK Transmit Shift Register UCPEN UCPAR UCMSB UC7BIT UCIREN UCIRTXPLx 6 0 1 IrDA Encoder UCAxTXD Transmit Clock Receive Clock BRCLK UCMODEx 2 UCSPB UCRXEIE UCRXBRKIE Set UCRXIFG Set UCTXIFG Set RXIFG www ti com eUSCI_A Introduction UART Mode 769 SLAU367P October 2012 Revised April 2020 Submit Documentatio...

Страница 770: ...mmended eUSCI_A initialization reconfiguration process is 1 Set UCSWRST BIS B UCSWRST UCAxCTL1 2 Initialize all eUSCI_A registers with UCSWRST 1 including UCAxCTL1 3 Configure ports 4 Clear UCSWRST through software BIC B UCSWRST UCAxCTL1 5 Enable interrupts optional through UCRXIE or UCTXIE 30 3 2 Character Format The UART character format see Figure 30 2 consists of a start bit seven or eight dat...

Страница 771: ...re can validate the address and must reset UCDORM to continue receiving data If UCDORM remains set only address characters are received When UCDORM is cleared during the reception of a character the receive interrupt flag is set after the reception completed The UCDORM bit is not modified automatically by the eUSCI_A hardware For address transmission in idle line multiprocessor format a precise id...

Страница 772: ...s bit is received but has a framing error or parity error the character is not transferred into UCAxRXBUF and UCRXIFG is not set If an address is received user software can validate the address and must reset UCDORM to continue receiving data If UCDORM remains set only address characters with address bit 1 are received The UCDORM bit is not modified by the eUSCI_A hardware automatically When UCDOR...

Страница 773: ...le time the synch timeout error flag UCSTOE is set The result can be read after the receive interrupt flag UCRXIFG is set Figure 30 6 Auto Baud Rate Detection Synch Field The UCDORM bit is used to control data reception in this mode When UCDORM is set all characters are received but not transferred into the UCAxRXBUF and interrupts are not generated When a break synch field is detected the UCBRK f...

Страница 774: ...ardware bit shaping for IrDA communication 30 3 5 1 IrDA Encoding The encoder sends a pulse for every zero bit in the transmit bitstream coming from the UART see Figure 30 7 The pulse duration is defined by UCIRTXPLx bits specifying the number of one half clock periods of the clock selected by UCIRTXCLK Figure 30 7 UART vs IrDA Data Format To set the pulse time of 3 16 bit period required by the I...

Страница 775: ...or UCPE A parity error is a mismatch between the number of 1s in a character and the value of the parity bit When an address bit is included in the character it is included in the parity calculation When a parity error is detected the UCPE bit is set Receive overrun UCOE An overrun error occurs when a character is loaded into UCAxRXBUF before the prior character has been read When an overrun occur...

Страница 776: ...eUSCI_A from being accidentally started Any glitch on UCAxRXD shorter than the deglitch time tt is ignored by the eUSCI_A and further action is initiated as shown in Figure 30 8 see the device specific data sheet for parameters The deglitch time tt can be set to four different values using the UCGLITx bits Figure 30 8 Glitch Suppression eUSCI_A Receive Not Started When a glitch is longer than tt o...

Страница 777: ...th higher frequencies and higher prescaler settings causes the majority votes to be taken in an increasingly smaller window and thus decrease the benefit of the majority vote In low frequency mode the baud rate generator uses one prescaler and one modulator to generate bit clock timing This combination supports fractional divisors for baud rate generation In this mode the maximum eUSCI_A baud rate...

Страница 778: ... the maximum eUSCI_A baud rate is 1 16 the UART source clock frequency BRCLK Modulation for BITCLK16 is based on the UCBRFx setting see Table 30 3 A 1 in the table indicates that the corresponding BITCLK16 period is one BRCLK period longer than the periods m 0 The modulation restarts with each new bit timing Modulation for BITCLK is based on the UCBRSx setting as previously described Table 30 3 BI...

Страница 779: ...can be used as a lookup table for finding the correct UCBRSx modulation pattern for the corresponding fractional part of N The values there are optimized for transmitting 1 The UCBRSx setting in one row is valid from the fractional portion given in that row until the one in the next row Table 30 4 UCBRSx Settings for Fractional Portion of N fBRCLK Baud Rate Fractional Portion of N UCBRSx 1 Fractio...

Страница 780: ...RSx settings Tbit TX i 1 fBRCLK UCBRx mUCBRSx i Where mUCBRSx i Modulation of bit i of UCBRSx 30 3 11 2 Oversampling Baud Rate Mode Bit Timing In oversampling baud rate mode calculation of the length of bit i Tbit TX i is based on the baud rate generator UCBRx UCBRFx and UCBRSx settings Where Sum of ones from the corresponding row in Table 30 3 mUCBRSx i Modulation of bit i of UCBRSx This results ...

Страница 781: ...e real sampling time tbit RX i is equal to the sum of all previous bits according to the formulas shown in the transmit timing section plus one half BITCLK for the current bit i plus the synchronization error tSYNC This results in the following tbit RX i for the low frequency baud rate mode Where Tbit RX i 1 fBRCLK UCBRx mUCBRSx i mUCBRSx i Modulation of bit i of UCBRSx For the oversampling baud r...

Страница 782: ... 1000000 9600 1 6 8 0x20 0 48 0 64 1 04 1 04 1000000 19200 1 3 4 0x2 0 8 0 96 1 84 1 84 1000000 38400 1 1 10 0x0 0 1 76 0 3 44 1000000 57600 0 17 0x4A 2 72 2 56 3 76 7 28 1000000 115200 0 8 0xD6 7 36 5 6 17 04 6 96 1048576 9600 1 6 13 0x22 0 46 0 42 0 48 1 23 1048576 19200 1 3 6 0xAD 0 88 0 83 2 36 1 18 1048576 38400 1 1 11 0x25 2 29 2 25 2 56 5 35 1048576 57600 0 18 0x11 2 3 37 5 31 5 55 1048576 ...

Страница 783: ... 57600 1 18 3 0x44 0 16 0 15 0 2 0 45 16777216 115200 1 9 1 0xB5 0 31 0 31 0 53 0 78 16777216 230400 1 4 8 0xEE 0 75 0 74 2 0 87 16777216 460800 1 2 4 0x92 1 62 1 37 3 56 2 06 20000000 9600 1 130 3 0x25 0 02 0 03 0 0 07 20000000 19200 1 65 1 0xD6 0 06 0 03 0 1 0 1 20000000 38400 1 32 8 0xEE 0 1 0 13 0 27 0 14 20000000 57600 1 21 11 0x22 0 16 0 13 0 16 0 38 20000000 115200 1 10 13 0xAD 0 29 0 26 0 ...

Страница 784: ...reak condition sets the UCBRK bit and the UCRXIFG flag 30 3 15 3 UART State Change Interrupt Operation Table 30 6 describes the UART state change interrupt flags Table 30 6 UART State Change Interrupt Flags Interrupt Flag Interrupt Condition UCSTTIFG START byte received interrupt This flag is set when the UART module receives a START byte This flag can be cleared by writing 0 to it UCTXCPTIFG Tran...

Страница 785: ...Vector 6 UCSTTIFG break case 0x08 Vector 8 UCTXCPTIFG break default break 30 3 16 DMA Operation In devices with a DMA controller the eUSCI module can trigger DMA transfers when the transmit buffer UCAxTXBUF is empty or when data was received in the UCAxRXBUF buffer The DMA trigger signals correspond to the UCTXIFG transmit interrupt flag and the UCRXIFG receive interrupt flag respectively The inte...

Страница 786: ... Control Word 1 Read write Word 0003h Section 30 4 2 06h UCAxBRW eUSCI_Ax Baud Rate Control Word Read write Word 0000h Section 30 4 3 06h UCAxBR0 1 eUSCI_Ax Baud Rate Control 0 Read write Byte 00h 07h UCAxBR1 eUSCI_Ax Baud Rate Control 1 Read write Byte 00h 08h UCAxMCTLW eUSCI_Ax Modulation Control Word Read write Word 00h Section 30 4 4 0Ah UCAxSTATW eUSCI_Ax Status Read write Word 00h Section 30...

Страница 787: ...ed when parity is disabled 0b Odd parity 1b Even parity 13 UCMSB RW 0h MSB first select Controls the direction of the receive and transmit shift register 0b LSB first 1b MSB first 12 UC7BIT RW 0h Character length Selects 7 bit or 8 bit character length 0b 8 bit data 1b 7 bit data 11 UCSPB RW 0h Stop bit select Number of stop bits 0b One stop bit 1b Two stop bits 10 9 UCMODEx RW 0h eUSCI_A mode The...

Страница 788: ...t frame transmitted is an address 1 UCTXBRK RW 0h Transmit break Transmits a break with the next write to the transmit buffer In UART mode with automatic baud rate detection 055h must be written into UCAxTXBUF to generate the required break synch fields Otherwise 0h must be written into the transmit buffer 0b Next frame transmitted is not a break 1b Next frame transmitted is a break or a break syn...

Страница 789: ...aud rate generator 30 4 4 UCAxMCTLW Register eUSCI_Ax Modulation Control Word Register Figure 30 15 UCAxMCTLW Register 15 14 13 12 11 10 9 8 UCBRSx rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 UCBRFx Reserved UCOS16 rw 0 rw 0 rw 0 rw 0 r0 r0 r0 rw 0 Can be modified only when UCSWRST 1 Table 30 11 UCAxMCTLW Register Description Bit Field Type Reset Description 15 8 UCBRSx RW 0h Second mo...

Страница 790: ...OE is cleared automatically when UCxRXBUF is read and must not be cleared by software Otherwise it does not function correctly 0b No error 1b Overrun error occurred 4 UCPE RW 0h Parity error flag When UCPEN 0 UCPE is read as 0 UCPE is cleared when UCAxRXBUF is read 0b No error 1b Character received with parity error 3 UCBRK RW 0h Break detect flag UCBRK is cleared when UCAxRXBUF is read 0b No brea...

Страница 791: ...the last received character from the receive shift register Reading UCAxRXBUF resets the receive error bits the UCADDR or UCIDLE bit and UCRXIFG In 7 bit data mode UCAxRXBUF is LSB justified and the MSB is always reset 30 4 7 UCAxTXBUF Register eUSCI_Ax Transmit Buffer Register Figure 30 18 UCAxTXBUF Register 15 14 13 12 11 10 9 8 Reserved r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 UCTXBUFx r...

Страница 792: ...nly when UCSWRST 1 Table 30 15 UCAxABCTL Register Description Bit Field Type Reset Description 15 6 Reserved R 0h Reserved 5 4 UCDELIMx RW 0h Break synch delimiter length 00b 1 bit time 01b 2 bit times 10b 3 bit times 11b 4 bit times 3 UCSTOE RW 0h Synch field time out error 0b No error 1b Length of synch field exceeded measurable time 2 UCBTOE RW 0h Break time out error 0b No error 1b Length of b...

Страница 793: ...gister Description Bit Field Type Reset Description 15 10 UCIRRXFLx RW 0h Receive filter length The minimum pulse length for receive is given by tMIN UCIRRXFLx 4 2 fIRTXCLK 9 UCIRRXPL RW 0h IrDA receive input UCAxRXD polarity 0b IrDA transceiver delivers a high pulse when a light pulse is seen 1b IrDA transceiver delivers a low pulse when a light pulse is seen 8 UCIRRXFE RW 0h IrDA receive filter ...

Страница 794: ...0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 Reserved UCTXCPTIE UCSTTIE UCTXIE UCRXIE r 0 r 0 r 0 r 0 rw 0 rw 0 rw 0 rw 0 Table 30 17 UCAxIE Register Description Bit Field Type Reset Description 15 4 Reserved R 0h Reserved 3 UCTXCPTIE RW 0h Transmit complete interrupt enable 0b Interrupt disabled 1b Interrupt enabled 2 UCSTTIE RW 0h Start bit interrupt enable 0b Interrupt disabled 1b Interrupt enabled 1 UCTX...

Страница 795: ...FG Register Description Bit Field Type Reset Description 15 4 Reserved R 0h Reserved 3 UCTXCPTIFG RW 0h Transmit complete interrupt flag UCTXCPTIFG is set when the entire byte in the internal shift register got shifted out and UCAxTXBUF is empty 0b No interrupt pending 1b Interrupt pending 2 UCSTTIFG RW 0h Start bit interrupt flag UCSTTIFG is set after a Start bit was received 0b No interrupt pend...

Страница 796: ... UCIVx r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCIVx r0 r0 r0 r0 r 0 r 0 r 0 r0 Table 30 19 UCAxIV Register Description Bit Field Type Reset Description 15 0 UCIVx R 0h eUSCI_A interrupt vector value 00h No interrupt pending 02h Interrupt Source Receive buffer full Interrupt Flag UCRXIFG Interrupt Priority Highest 04h Interrupt Source Transmit buffer empty Interrupt Flag UCTXIFG 06h Interrupt Sour...

Страница 797: ... Interface eUSCI SPI Mode The enhanced universal serial communication interfaces eUSCI_A and eUSCI_B support multiple serial communication modes with one hardware module This chapter discusses the operation of the synchronous peripheral interface SPI mode Topic Page 31 1 Enhanced Universal Serial Communication Interfaces eUSCI_A eUSCI_B Overview 798 31 2 eUSCI Introduction SPI Mode 798 31 3 eUSCI ...

Страница 798: ...ce to an external system through three or four pins UCxSIMO UCxSOMI UCxCLK and UCxSTE SPI mode is selected when the UCSYNC bit is set and SPI mode 3 pin or 4 pin is selected with the UCMODEx bits SPI mode features include 7 bit or 8 bit data length LSB first or MSB first data transmit and receive 3 pin and 4 pin SPI operation Master or slave modes Independent transmit and receive shift registers S...

Страница 799: ...r UCMSB UC7BIT BRCLK Set UCxRXIFG Set UCxTXIFG 0 1 UCLISTEN Clock Direction Phase and Polarity UCCKPH UCCKPL UCxSIMO UCxCLK Set UCOE Transmit Enable Control UCSTEM UCxSTE Set UCFE 2 UCMODEx www ti com eUSCI Introduction SPI Mode 799 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Enhanced Universal Serial Communication Inter...

Страница 800: ...UCxSTE operation Table 31 1 UCxSTE Operation UCMODEx UCxSTE Active State UCxSTE Slave Master 01 High 0 Inactive Active 1 Active Inactive 10 Low 0 Active Inactive 1 Inactive Active 31 3 1 eUSCI Initialization and Reset The eUSCI is reset by a PUC or by the UCSWRST bit After a PUC the UCSWRST bit is automatically set keeping the eUSCI in a reset condition When set the UCSWRST bit resets the UCRXIE U...

Страница 801: ...as a master in both 3 pin and 4 pin configurations The eUSCI initiates data transfer when data is moved to the transmit data buffer UCxTXBUF The UCxTXBUF data is moved to the transmit TX shift register when the TX shift register is empty initiating data transfer on UCxSIMO starting with either the MSB or LSB depending on the UCMSB setting Data on UCxSOMI is shifted into the receive shift register ...

Страница 802: ...ritten into UCxTXBUF to be transferred when UCxSTE transitions back to the master active state The UCxSTE input signal is not used in 3 pin master mode 31 3 3 2 4 Pin SPI Master Mode UCSTEM 1 If UCSTEM 1 in 4 pin master mode UCxSTE is a digital output In this mode the slave enable signal for a single slave is automatically generated on UCxSTE The corresponding behavior can be seen in Figure 31 4 I...

Страница 803: ...clock and in 4 pin mode when the UCxSTE is in the slave active state 31 3 5 2 Receive Enable The SPI receives data when a transmission is active Receive and transmit operations operate concurrently 31 3 6 Serial Clock Control UCxCLK is provided by the master on the SPI bus When UCMST 1 the bit clock is provided by the eUSCI bit clock generator on the UCxCLK pin The clock used to generate the bit c...

Страница 804: ...se the clock is provided by the external master It is possible to operate the eUSCI in SPI slave mode while the device is in LPM4 and all clock sources are disabled The receive or transmit interrupt can wake up the CPU from any low power mode 31 3 8 eUSCI Interrupts in SPI Mode The eUSCI has only one interrupt vector that is shared for transmission and for reception eUSCI_Ax and eUSCI_Bx do not sh...

Страница 805: ...ram counter PC to automatically enter the appropriate software routine Disabled interrupts do not affect the UCxIV value Any access read or write of the UCxIV register automatically resets the highest pending interrupt flag If another interrupt flag is set another interrupt is immediately generated after servicing the initial interrupt 31 3 8 3 1 UCxIV Software Example The following software examp...

Страница 806: ...Word 0001h Section 31 4 1 00h UCAxCTL1 eUSCI_Ax Control 1 Read write Byte 01h 01h UCAxCTL0 eUSCI_Ax Control 0 Read write Byte 00h 06h UCAxBRW eUSCI_Ax Bit Rate Control Word Read write Word 0000h Section 31 4 2 06h UCAxBR0 eUSCI_Ax Bit Rate Control 0 Read write Byte 00h 07h UCAxBR1 eUSCI_Ax Bit Rate Control 1 Read write Byte 00h 0Ah UCAxSTATW eUSCI_Ax Status Read write Word 00h Section 31 4 3 0Ch U...

Страница 807: ...shift register 0b LSB first 1b MSB first 12 UC7BIT RW 0h Character length Selects 7 bit or 8 bit character length 0b 8 bit data 1b 7 bit data 11 UCMST RW 0h Master mode select 0b Slave mode 1b Master mode 10 9 UCMODEx RW 0h eUSCI mode The UCMODEx bits select the synchronous mode when UCSYNC 1 00b 3 pin SPI 01b 4 pin SPI with UCxSTE active high Slave enabled when UCxSTE 1 10b 4 pin SPI with UCxSTE ...

Страница 808: ...e eUSCI SPI Mode 31 4 2 UCAxBRW Register eUSCI_Ax Bit Rate Control Register 1 Figure 31 6 UCAxBRW Register 15 14 13 12 11 10 9 8 UCBRx rw rw rw rw rw rw rw rw 7 6 5 4 3 2 1 0 UCBRx rw rw rw rw rw rw rw rw Can be modified only when UCSWRST 1 Table 31 4 UCAxBRW Register Description Bit Field Type Reset Description 15 0 UCBRx RW 0h Bit clock prescaler setting fBitClock fBRCLK UCBRx If UCBRx 0 fBitClo...

Страница 809: ...TEN RW 0h Listen enable The UCLISTEN bit selects loopback mode 0b Disabled 1b Enabled The transmitter output is internally fed back to the receiver 6 UCFE RW 0h Framing error flag This bit indicates a bus conflict in 4 wire master mode UCFE is not used in 3 wire master or any slave mode 0b No error 1b Bus conflict occurred 5 UCOE RW 0h Overrun error flag This bit is set when a character is transfe...

Страница 810: ... 8 UCAxRXBUF Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCRXBUFx rw rw rw rw rw rw rw rw Table 31 6 UCAxRXBUF Register Description Bit Field Type Reset Description 15 8 Reserved R 0h Reserved 7 0 UCRXBUFx R 0h The receive data buffer is user accessible and contains the last received character from the receive shift register Reading UCxRXBUF resets the receive e...

Страница 811: ...31 9 UCAxTXBUF Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCTXBUFx rw rw rw rw rw rw rw rw Table 31 7 UCAxTXBUF Register Description Bit Field Type Reset Description 15 8 Reserved R 0h Reserved 7 0 UCTXBUFx RW 0h The transmit data buffer is user accessible and holds the data waiting to be moved into the transmit shift register and transmitted Writing to the tra...

Страница 812: ..._Ax Interrupt Enable Register Figure 31 10 UCAxIE Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved UCTXIE UCRXIE r 0 r 0 r 0 r 0 r 0 r 0 rw 0 rw 0 Table 31 8 UCAxIE Register Description Bit Field Type Reset Description 15 2 Reserved R 0h Reserved 1 UCTXIE RW 0h Transmit interrupt enable 0b Interrupt disabled 1b Interrupt enabled 0 UCRXIE RW 0h Receive interr...

Страница 813: ...gister 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved UCTXIFG UCRXIFG r 0 r 0 r 0 r 0 r 0 r 0 rw 1 rw 0 Table 31 9 UCAxIFG Register Description Bit Field Type Reset Description 15 2 Reserved R 0h Reserved 1 UCTXIFG RW 1h Transmit interrupt flag UCTXIFG is set when UCxxTXBUF empty 0b No interrupt pending 1b Interrupt pending 0 UCRXIFG RW 0h Receive interrupt flag UC...

Страница 814: ...ector Register Figure 31 12 UCAxIV Register 15 14 13 12 11 10 9 8 UCIVx r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCIVx r0 r0 r0 r 0 r 0 r 0 r 0 r0 Table 31 10 UCAxIV Register Description Bit Field Type Reset Description 15 0 UCIVx R 0h eUSCI interrupt vector value 000h No interrupt pending 002h Interrupt Source Data received Interrupt Flag UCRXIFG Interrupt Priority Highest 004h Interrupt Source Tr...

Страница 815: ... Word 01C1h Section 31 5 1 00h UCBxCTL1 eUSCI_Bx Control 1 Read write Byte C1h 01h UCBxCTL0 eUSCI_Bx Control 0 Read write Byte 01h 06h UCBxBRW eUSCI_Bx Bit Rate Control Word Read write Word 0000h Section 31 5 2 06h UCBxBR0 eUSCI_Bx Bit Rate Control 0 Read write Byte 00h 07h UCBxBR1 eUSCI_Bx Bit Rate Control 1 Read write Byte 00h 08h UCBxSTATW eUSCI_Bx Status Read write Word 00h Section 31 5 3 0Ch ...

Страница 816: ...t shift register 0b LSB first 1b MSB first 12 UC7BIT RW 0h Character length Selects 7 bit or 8 bit character length 0b 8 bit data 1b 7 bit data 11 UCMST RW 0h Master mode select 0b Slave mode 1b Master mode 10 9 UCMODEx RW 0h eUSCI mode The UCMODEx bits select the synchronous mode when UCSYNC 1 00b 3 pin SPI 01b 4 pin SPI with UCxSTE active high Slave enabled when UCxSTE 1 10b 4 pin SPI with UCxST...

Страница 817: ... Reserved UCBUSY rw 0 rw 0 rw 0 r0 r0 r0 r0 r 0 Can be modified only when UCSWRST 1 Table 31 14 UCBxSTATW Register Description Bit Field Type Reset Description 15 8 Reserved R 0h Reserved 7 UCLISTEN RW 0h Listen enable The UCLISTEN bit selects loopback mode 0b Disabled 1b Enabled The transmitter output is internally fed back to the receiver 6 UCFE RW 0h Framing error flag This bit indicates a bus ...

Страница 818: ...ccessible and contains the last received character from the receive shift register Reading UCxRXBUF resets the receive error bits and UCRXIFG In 7 bit data mode UCxRXBUF is LSB justified and the MSB is always reset 31 5 5 UCBxTXBUF Register eUSCI_Bx Transmit Buffer Register Figure 31 17 UCBxTXBUF Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCTXBUFx rw rw rw rw r...

Страница 819: ...IE RW 0h Transmit interrupt enable 0b Interrupt disabled 1b Interrupt enabled 0 UCRXIE RW 0h Receive interrupt enable 0b Interrupt disabled 1b Interrupt enabled 31 5 7 UCBxIFG Register eUSCI_Bx Interrupt Flag Register Figure 31 19 UCBxIFG Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 Reserved UCTXIFG UCRXIFG r 0 r 0 r 0 r 0 r 0 r 0 rw 1 rw 0 Table 31 18 UCBxIFG Re...

Страница 820: ...ctor Register Figure 31 20 UCBxIV Register 15 14 13 12 11 10 9 8 UCIVx r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCIVx r0 r0 r0 r 0 r 0 r 0 r 0 r0 Table 31 19 UCBxIV Register Description Bit Field Type Reset Description 15 0 UCIVx R 0h eUSCI interrupt vector value 0000h No interrupt pending 0002h Interrupt Source Data received Interrupt Flag UCRXIFG Interrupt Priority Highest 0004h Interrupt Source ...

Страница 821: ...hanced Universal Serial Communication Interface eUSCI I2 C Mode The enhanced universal serial communication interface B eUSCI_B supports multiple serial communication modes with one hardware module This chapter discusses the operation of the I2 C mode Topic Page 32 1 Enhanced Universal Serial Communication Interface B eUSCI_B Overview 822 32 2 eUSCI_B Introduction I2 C Mode 822 32 3 eUSCI_B Operat...

Страница 822: ...ices connected by the two wire I2 C serial bus External components attached to the I2 C bus serially transmit or receive serial data to or from the eUSCI_B module through the 2 wire I2 C interface The eUSCI_B I2 C mode features include 7 bit and 10 bit device addressing modes General call START RESTART STOP Multi master transmitter or receiver mode Slave receiver or transmitter mode Standard mode ...

Страница 823: ...2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Enhanced Universal Serial Communication Interface eUSCI I2 C Mode Figure 32 1 eUSCI_B Block Diagram I2 C Mode 32 3 eUSCI_B Operation I2 C Mode The I2 C mode supports any slave or master I2 C compatible device Figure 32 2 shows an example of an I2 C bus Each I2 C device is recognized by a unique address and can op...

Страница 824: ...re the eUSCI_B module only when UCSWRST is set Setting UCSWRST in I2 C mode has the following effects I2 C communication stops SDA and SCL are high impedance UCBxSTAT bits 15 8 and 6 4 are cleared Registers UCBxIE and UCBxIFG are cleared All other bits and registers remain unchanged NOTE Initializing or reconfiguring the eUSCI_B module The recommended eUSCI_B initialization reconfiguration process...

Страница 825: ...ter a STOP Data on SDA must be stable during the high period of SCL see Figure 32 4 The high and low state of SDA can change only when SCL is low otherwise START or STOP conditions are generated Figure 32 4 Bit Transfer on I2 C Bus 32 3 3 I2 C Addressing Modes The I2 C mode supports 7 bit and 10 bit addressing modes 32 3 3 1 7 Bit Addressing In the 7 bit addressing format see Figure 32 5 the first...

Страница 826: ... web under Code Examples To set up the eUSCI_B as a master transmitter that transmits to a slave with the address 0x12h only a few steps are needed see Example 32 1 Example 32 1 Master TX With 7 Bit Address UCBxCTL1 UCSWRST put eUSCI_B in reset state UCBxCTLW0 UCMODE_3 UCMST I2C master mode UCBxBRW 0x0008 baud rate SMCLK 8 UCBxCTLW1 UCASTP_2 automatic STOP assertion UCBxTBCNT 0x07 TX 7 bytes of da...

Страница 827: ...d transmit requests the according bits in UCBxIE and at the end GIE need to be set Finally the ports must be configured This step is device dependent see the data sheet for the pins that are used The RX interrupt service routine is called for every byte received by a master device The TX interrupt service routine is executed each time the master requests a byte The recommended structure of the int...

Страница 828: ...d in UCBxI2COA0 The UCSTTIFG flag is set when address received matches the eUSCI_B slave address 32 3 5 1 1 I2 C Slave Transmitter Mode Slave transmitter mode is entered when the slave address transmitted by the master is identical to its own address with a set R W bit The slave transmitter shifts the serial data out on SDA with the clock pulses that are generated by the master device The slave de...

Страница 829: ... the clock pulses that are generated by the master device The slave device does not generate the clock but it can hold SCL low if intervention of the CPU is required after a byte has been received If the slave receives data from the master the eUSCI_B module is automatically configured as a receiver and UCTR is cleared After the first data byte is received the receive interrupt flag UCRXIFG0 is se...

Страница 830: ...right 2012 2020 Texas Instruments Incorporated Enhanced Universal Serial Communication Interface eUSCI I2 C Mode If the master generates a repeated START condition the eUSCI_B I2 C state machine returns to its address reception state Figure 32 10 shows the I2 C slave receiver operation Figure 32 10 I2 C Slave Receiver Mode 32 3 5 1 3 I2 C Slave 10 Bit Addressing Mode The 10 bit addressing mode is ...

Страница 831: ...ode 32 3 5 2 Master Mode The eUSCI_B module is configured as an I2 C master by selecting the I2 C mode with UCMODEx 11 and UCSYNC 1 and setting the UCMST bit When the master is part of a multi master system UCMM must be set and its own address must be programmed into the UCBxI2COA0 register Support for multiple slave addresses is explained in Section 32 3 9 When UCA10 0 7 bit addressing is selecte...

Страница 832: ... UCTXSTT bit is not set Setting UCTXSTP generates a STOP condition after the next acknowledge from the slave If UCTXSTP is set during the transmission of the slave address or while the eUSCI_B module waits for data to be written into UCBxTXBUF a STOP condition is generated even if no data was transmitted to the slave In this case the UCSTPIFG is set When transmitting a single byte of data the UCTX...

Страница 833: ...continues A UCALIFG 1 UCMST 0 UCTR 0 Receiver UCSTTIFG 1 UCGC 1 if general call USCI continues as Slave Receiver Not acknowledge received after a data byte UCTXSTT 0 UCTXSTP 0 UCTXSTP 0 UCALIFG 1 UCMST 0 Bus stalled SCL held low until data available Write data to UCBxTXBUF 1 UCTR 1 Transmitter 2 UCTXSTT 1 UCTXIFG 1 UCBxTXBUF discarded UCTXSTT 0 UCNACKIFG 1 UCBxTXBUF discarded UCTXIFG 1 UCBxTXBUF d...

Страница 834: ...IFG is set If UCBxRXBUF is not read the master holds the bus during reception of the last data bit and until the UCBxRXBUF is read If the slave does not acknowledge the transmitted address the not acknowledge interrupt flag UCNACKIFG is set The master must react with either a STOP condition or a repeated START condition A STOP condition is either generated by the automatic STOP generation or by se...

Страница 835: ...R 0 Receiver 2 UCTXSTT 1 Arbitration lost in slave address or data byte A Other master continues UCALIFG 1 UCMST 0 Arbitration lost and addressed as slave Other master continues A UCALIFG 1 UCMST 0 UCTR 1 Transmitter UCSTTIFG 1 UCTXIFG 1 USCI continues as Slave Transmitter A A A UCTXSTT 0 UCTXSTP 0 UCTXIFG 1 UCALIFG 1 UCMST 0 UCTXSTP 1 UCTXSTP 0 www ti com eUSCI_B Operation I2 C Mode 835 SLAU367P ...

Страница 836: ...ion on the bus an arbitration procedure is invoked Figure 32 15 shows the arbitration procedure between two devices The arbitration procedure uses the data presented on SDA by the competing transmitters The first master transmitter that generates a logic high is overruled by the opposing master generating a logic low The arbitration procedure gives priority to the device that transmits the serial ...

Страница 837: ...he eUSCI_B clock source BRCLK The maximum bit clock that can be used in single master mode is fBRCLK 4 In multi master mode the maximum bit clock is fBRCLK 8 The BITCLK frequency is given by fBitClock fBRCLK UCBRx The minimum high and low periods of the generated SCL are tLOW MIN tHIGH MIN UCBRx 2 fBRCLK when UCBRx is even tLOW MIN tHIGH MIN UCBRx 1 2 fBRCLK when UCBRx is odd The eUSCI_B clock sou...

Страница 838: ...k is stretched by the eUSCI_B under the following conditions The internal shift register is expecting data but the TXIFG is still pending The internal shift register is full but the RXIFG is still pending The arbitration lost interrupt is pending UCSWACK is selected and UCBxI2COA0 did cause a match To avoid clock stretching all of these situations for clock stretch either need to be avoided or the...

Страница 839: ...er is also incremented at the second bit position if an arbitration lost occurs during the first bit of data 32 3 8 1 Byte Counter Interrupt If UCASTPx 01 or 10 the UCBCNTIFG is set when the byte counter threshold value UCBxTBCNT is reached in both master and slave mode Writing zero to UCBxTBCNT does not generate an interrupt Because the UCBCNTIFG has a lower interrupt priority than the UCBTXIFG a...

Страница 840: ...ASK the eUSCI_B module considers the received address as its own address If UCSWACK 0 the module sends an acknowledge automatically If UCSWACK 1 the user software must evaluate the received address in register UCBxADDRX after the UCSTTIFG is set To acknowledge the received address the software must set UCTXACK to 1 The eUSCI_B module also automatically acknowledges a slave address that is seen on ...

Страница 841: ...UCASTPx 10 the UCTXIFG0 is set as many times as defined in UCBxTBCNT An interrupt request is generated if UCTXIEx and GIE are also set UCTXIFGx is automatically reset if a write to UCBxTXBUF occurs or if the UCALIFG is cleared UCTXIFGx is set when Master mode UCTXSTT was set by the user Slave mode own address was received UCETXINT 0 or START was received UCETXINT 1 UCTXIEx is reset after a PUC or ...

Страница 842: ...Byte counter interrupt This flag is set when the byte counter value reaches the value defined in UCBxTBCNT and UCASTPx 01 or 10 This bit allows to organize following communications especially if a RESTART will be issued UCSTTIFG START condition detected interrupt This flag is set when the I2 C module detects a START condition together with its own address 1 UCSTTIFG is used in slave mode only UCST...

Страница 843: ...0x1e case 0x00 Vector 0 No interrupts break case 0x02 Vector 2 ALIFG break case 0x04 Vector 4 NACKIFG break case 0x06 Vector 6 STTIFG break case 0x08 Vector 8 STPIFG break case 0x0a Vector 10 RXIFG3 break case 0x0c Vector 12 TXIFG3 break case 0x0e Vector 14 RXIFG2 break case 0x10 Vector 16 TXIFG2 break case 0x12 Vector 18 RXIFG1 break case 0x14 Vector 20 TXIFG1 break case 0x16 Vector 22 RXIFG0 bre...

Страница 844: ... eUSCI_Bx Status Word Read Word 0000h Section 32 4 4 08h UCBxSTAT eUSCI_Bx Status Read Byte 00h 09h UCBxBCNT eUSCI_Bx Byte Counter Register Read Byte 00h 0Ah UCBxTBCNT eUSCI_Bx Byte Counter Threshold Register Read Write Word 00h Section 32 4 5 0Ch UCBxRXBUF eUSCI_Bx Receive Buffer Read write Word 00h Section 32 4 6 0Eh UCBxTXBUF eUSCI_Bx Transmit Buffer Read write Word 00h Section 32 4 7 14h UCBxI...

Страница 845: ...master in the system The address compare unit is disabled 1b Multi master environment 12 Reserved R 0h Reserved 11 UCMST RW 0h Master mode select When a master loses arbitration in a multi master environment UCMM 1 the UCMST bit is automatically cleared and the module acts as slave 0b Slave mode 1b Master mode 10 9 UCMODEx RW 0h eUSCI_B mode The UCMODEx bits select the synchronous mode when UCSYNC...

Страница 846: ...h Transmit STOP condition in master mode Ignored in slave mode In master receiver mode the STOP condition is preceded by a NACK UCTXSTP is automatically cleared after STOP is generated This bit is a don t care if automatic UCASTPx is different from 01 or 10 0b No STOP generated 1b Generate STOP 1 UCTXSTT RW 0h Transmit START condition in master mode Ignored in slave mode In master receiver mode a ...

Страница 847: ...b 165000 MODCLK cycles approximately 34 ms 5 UCSTPNACK RW 0h The UCSTPNACK bit allows to make the eUSCI_B master acknowledge the last byte in master receiver mode as well This does not conform to the I2C specification and should only be used for slaves that automatically release the SDA after a fixed packet length Modify only when UCSWRST 1 0b Send a not acknowledge before the STOP condition as a ...

Страница 848: ...tation Feedback Copyright 2012 2020 Texas Instruments Incorporated Enhanced Universal Serial Communication Interface eUSCI I2 C Mode Table 32 5 UCBxCTLW1 Register Description continued Bit Field Type Reset Description 1 0 UCGLITx RW 0h Deglitch time 00b 50 ns 01b 25 ns 10b 12 5 ns 11b 6 25 ns ...

Страница 849: ...er 15 14 13 12 11 10 9 8 UCBCNTx r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 Reserved UCSCLLOW UCGC UCBBUSY Reserved r0 r 0 r 0 r 0 r 0 r0 r0 r0 Table 32 7 UCBxSTATW Register Description Bit Field Type Reset Description 15 8 UCBCNTx R 0h Hardware byte counter value Reading this register returns the number of bytes received or transmitted on the I2C Bus since the last START or RESTART There is ...

Страница 850: ...NT Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCTBCNTx rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 Can be modified only when UCSWRST 1 Table 32 8 UCBxTBCNT Register Description Bit Field Type Reset Description 15 8 Reserved R 0h Reserved 7 0 UCTBCNTx RW 0h The byte counter threshold value is used to set the number of I2C data bytes after which the automatic STOP or...

Страница 851: ...ved R 0h Reserved 7 0 UCRXBUFx R 0h The receive data buffer is user accessible and contains the last received character from the receive shift register Reading UCBxRXBUF resets the UCRXIFGx flags 32 4 7 UCBxTXBUF eUSCI_Bx Transmit Buffer Register Figure 32 23 UCBxTXBUF Register 15 14 13 12 11 10 9 8 Reserved r0 r0 r0 r0 r0 r0 r0 r0 7 6 5 4 3 2 1 0 UCTXBUFx rw rw rw rw rw rw rw rw Table 32 10 UCBxT...

Страница 852: ...ption 15 UCGCEN RW 0h General call response enable This bit is only available in UCBxI2COA0 Modify only when UCSWRST 1 0b Do not respond to a general call 1b Respond to a general call 14 11 Reserved R 0h Reserved 10 UCOAEN RW 0h Own Address enable register With this register it can be selected if the I2C slave address related to this register UCBxI2COA0 is evaluated or not Modify only when UCSWRST...

Страница 853: ...local address of the eUSCIx_B I2C controller The address is right justified In 7 bit addressing mode bit 6 is the MSB and bits 9 7 are ignored In 10 bit addressing mode bit 9 is the MSB Modify only when UCSWRST 1 32 4 10 UCBxI2COA2 Register eUSCI_Bx I2C Own Address 2 Register Figure 32 26 UCBxI2COA2 Register 15 14 13 12 11 10 9 8 Reserved UCOAEN I2COA2 rw 0 r0 r0 r0 r0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1...

Страница 854: ...ot Modify only when UCSWRST 1 0b The slave address defined in I2COA3 is disabled 1b The slave address defined in I2COA3 is enabled 9 0 I2COA3 RW 0h I2C own address The I2COA3 bits contain the local address of the eUSCIx_B I2C controller The address is right justified In 7 bit addressing mode bit 6 is the MSB and bits 9 7 are ignored In 10 bit addressing mode bit 9 is the MSB Modify only when UCSWR...

Страница 855: ...bit is a don t care when comparing the address on the bus to the own address Using this method it is possible to react on more than one slave address When all bits of ADDMASKx are set the address mask feature is deactivated Modify only when UCSWRST 1 32 4 14 UCBxI2CSA Register eUSCI_Bx I2C Slave Address Register Figure 32 30 UCBxI2CSA Register 15 14 13 12 11 10 9 8 Reserved I2CSAx r 0 r0 r0 r0 r0 ...

Страница 856: ... 0h Transmit interrupt enable 3 0b Interrupt disabled 1b Interrupt enabled 12 UCRXIE3 RW 0h Receive interrupt enable 3 0b Interrupt disabled 1b Interrupt enabled 11 UCTXIE2 RW 0h Transmit interrupt enable 2 0b Interrupt disabled 1b Interrupt enabled 10 UCRXIE2 RW 0h Receive interrupt enable 2 0b Interrupt disabled 1b Interrupt enabled 9 UCTXIE1 RW 0h Transmit interrupt enable 1 0b Interrupt disabl...

Страница 857: ...Communication Interface eUSCI I2 C Mode Table 32 18 UCBxIE Register Description continued Bit Field Type Reset Description 2 UCSTTIE RW 0h START condition interrupt enable 0b Interrupt disabled 1b Interrupt enabled 1 UCTXIE0 RW 0h Transmit interrupt enable 0 0b Interrupt disabled 1b Interrupt enabled 0 UCRXIE0 RW 0h Receive interrupt enable 0 0b Interrupt disabled 1b Interrupt enabled ...

Страница 858: ...s defined in UCBxI2COA3 was on the bus in the same frame 0b No interrupt pending 1b Interrupt pending 11 UCTXIFG2 RW 0h eUSCI_B transmit interrupt flag 2 UCTXIFG2 is set when UCBxTXBUF is empty in slave mode if the slave address defined in UCBxI2COA2 was on the bus in the same frame 0b No interrupt pending 1b Interrupt pending 10 UCRXIFG2 RW 0h Receive interrupt flag 2 UCRXIFG2 is set when UCBxRXB...

Страница 859: ...upt pending 1b Interrupt pending 3 UCSTPIFG RW 0h STOP condition interrupt flag 0b No interrupt pending 1b Interrupt pending 2 UCSTTIFG RW 0h START condition interrupt flag 0b No interrupt pending 1b Interrupt pending 1 UCTXIFG0 RW 0h eUSCI_B transmit interrupt flag 0 UCTXIFG0 is set when UCBxTXBUF is empty in master mode or in slave mode if the slave address defined in UCBxI2COA0 was on the bus i...

Страница 860: ...rrupt Priority Highest 04h Interrupt Source Not acknowledgment Interrupt Flag UCNACKIFG 06h Interrupt Source Start condition received Interrupt Flag UCSTTIFG 08h Interrupt Source Stop condition received Interrupt Flag UCSTPIFG 0Ah Interrupt Source Slave 3 Data received Interrupt Flag UCRXIFG3 0Ch Interrupt Source Slave 3 Transmit buffer empty Interrupt Flag UCTXIFG3 0Eh Interrupt Source Slave 2 Da...

Страница 861: ... Revised April 2020 REF_A The REF_A module is a general purpose reference system that generates the voltage references required for other subsystems such as digital to analog converters analog to digital converters or comparators This chapter describes the REF_A module Topic Page 33 1 REF_A Introduction 862 33 2 Principle of Operation 863 33 3 REF_A Registers 865 ...

Страница 862: ...es that can be used by various analog peripherals in a given device The heart of the reference system is the bandgap from which all other references are derived by unity or noninverting gain stages The REFGEN subsystem consists of the bandgap the bandgap bias and the noninverting buffer stage which generates the three primary voltage reference available in the system 1 2 V 2 0 V and 2 5 V In addit...

Страница 863: ...module requests sampled mode For example any module using the gray box in the block diagram requests static mode and causes all other modules to use static mode In other words static mode always has higher priority than sampled mode 33 2 2 Reference System Requests There are three basic reference system requests that are used by the reference system Each module can use these requests to obtain the...

Страница 864: ... is using the reference and that no changes should be made to the reference settings For example during an active ADC12_B conversion the reference voltage level should not be changed REFGENBUSY is asserted when there is an active ADC12_B conversion ADC12BUSY 1 REFGENBUSY when asserted write protects the REFCTL register This prevents the reference from being disabled or its level changed during any...

Страница 865: ...e address offset is listed in Table 33 1 NOTE All registers have word or byte register access For a generic registerANYREG the suffix _L ANYREG_L refers to the lower byte of the register bits 0 through 7 The suffix _H ANYREG_H refers to the upper byte of the register bits 8 through 15 Table 33 1 REF_A Registers Offset Acronym Register Name Type Access Reset Section 00h REFCTL0 REFCTL0 Read write W...

Страница 866: ...to be used 1b Reference voltage output is ready to be used 11 BGMODE R 0h Bandgap mode Read only 0b Static mode 1b Sampled mode 10 REFGENBUSY R 0h Reference generator busy Read only 0b Reference generator not busy 1b Reference generator busy 9 REFBGACT R 0h Reference bandgap active Read only 0b Reference bandgap buffer not active 1b Reference bandgap buffer active 8 REFGENACT R 0h Reference genera...

Страница 867: ...dependent of this control bit Can be modified only when REFGENBUSY 0 0b Temperature sensor enabled 1b Temperature sensor disabled to save power 2 Reserved R 0h Reserved Always reads as 0 1 REFOUT RW 0h Reference output buffer On devices with an ADC10_A this bit must be written with 0 Can be modified only when REFGENBUSY 0 0b Reference output not available externally 1b Reference output available e...

Страница 868: ...Incorporated ADC12_B Chapter 34 SLAU367P October 2012 Revised April 2020 ADC12_B The ADC12_B module is a high performance 12 bit analog to digital converter ADC This chapter describes the operation of the ADC12_B module Topic Page 34 1 ADC12_B Introduction 869 34 2 ADC12_B Operation 871 34 3 ADC12_B Registers 887 ...

Страница 869: ...reference voltage generation 1 2 V 2 0 V or 2 5 V with option to make available externally Software selectable internal or external reference Up to 32 individually configurable external input channels with single ended or differential input selection available Internal conversion channels for internal temperature sensor and 1 2 AVCC and four more internal channels available on select devices see t...

Страница 870: ...ternal A31 external A27 external A29 external A28 external A30 AVSS Reference Voltage Select Internal 3 Internal 2 Internal 0 BUF_INT REFOUT Internal 1 REFOUT and ADC12VRSEL bit 0 1 REFOUT 0 ADC12VRSEL bits 1 3 external A26 1 0 ADC12CH3MAP 1 0 ADC12CH2MAP 1 0 ADC12CH1MAP 1 0 ADC12CH0MAP 1 0 ADC12TCMAP 1 0 ADC12BATMAP A31 A30 A29 A28 A27 A26 000 001 111 11110 11101 11100 11011 11010 Copyright 2017 ...

Страница 871: ...voltage at which the ADC output saturates for differential mode where VR Vin VR VR Vin VR 16 Four control registers configure the ADC12_B core ADC12CTL0 ADC12CTL1 ADC12CTL2 and ADC12CTL3 The ADC12ON bit enables or disables the core The ADC12_B can be turned off when it is not in use to save power If the ADC12ON bit is set to 0 during a conversion the conversion is abruptly exited and the module is...

Страница 872: ...e redistribution method When the inputs are internally switched the switching action may cause transients on the input signal These transients decay and settle before causing errant conversion Figure 34 2 Analog Multiplexer T Switch 34 2 2 1 Analog Port Selection The ADC12_B inputs are multiplexed with digital port pins When analog signals are applied to digital gates parasitic current can flow fr...

Страница 873: ...he ADC12ISSH bit The SHSx bits select the source for SHI and include the following ADC12SC bit Up to seven other sources that may include timer output see to the device specific data sheet for available sources The ADC12_B supports 8 bit 10 bit and 12 bit resolution modes and the ADC12RES bits select the current mode The analog to digital conversion requires 10 12 and 14 ADC12CLK cycles respective...

Страница 874: ...ample Mode With Internal Reference in 12 Bit Mode 34 2 6 2 Pulse Sample Mode ADC12SHP 1 selects the pulse sample mode The SHI signal triggers the sampling timer The ADC12SHT0x and ADC12SHT1x bits in ADC12CTL0 control the interval of the sampling timer that defines the SAMPCON sample period tsample The sampling timer keeps SAMPCON high while waiting for reference and ADC local reference buffer to s...

Страница 875: ...w ti com ADC12_B Operation 875 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated ADC12_B Figure 34 5 Pulse Sample Mode First Conversion or Where ADC12MSC 0 in 12 Bit Mode Figure 34 6 Pulse Sample Mode Subsequent Conversions in 12 Bit Mode 34 2 6 3 Sample Timing Considerations When SAMPCON 0 all Ax inputs are high impedance Whe...

Страница 876: ...The sequence continues until an ADC12EOS bit in ADC12MCTLx is processed this is the last control byte processed When conversion results are written to a selected ADC12MEMx the corresponding flag in the ADC12IFGRx register is set There are two formats available to read the conversion result from ADC12MEMx When ADC12DF 0 the conversion is right justified and unsigned For ADC12DF 0 with ADC12DIF 0 an...

Страница 877: ...lected by the CONSEQx bits All state diagrams assume a 12 bit resolution setting Table 34 2 Conversion Mode Summary ADC12CONSEQx Mode Operation 00 Single channel single conversion A single channel is converted once 01 Sequence of channels autoscan A sequence of channels is converted once 10 Repeat single channel A single channel is converted repeatedly 11 Repeat sequence of channels repeated autos...

Страница 878: ... ADC12_B 34 2 8 1 Single Channel Single Conversion Mode A single channel is sampled and converted once The ADC result is written to the ADC12MEMx that is defined by the CSTARTADDx bits Figure 34 8 shows the flow of the single channel single conversion mode when RES 0x2 for 12 bit mode When ADC12SC triggers a conversion the ADC12SC bit can trigger successive conversions When any other trigger sourc...

Страница 879: ...B 34 2 8 2 Sequence of Channels Mode Autoscan Mode In sequence of channels mode also called autoscan mode a sequence of channels is sampled and converted once The ADC results are written to the conversion memories starting with the ADC12MEMx that is defined by the CSTARTADDx bits The sequence stops after the measurement of the channel with a set ADC12EOS bit Figure 34 9 shows the sequence of chann...

Страница 880: ...B Operation www ti com 880 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated ADC12_B 34 2 8 3 Repeat Single Channel Mode In repeat single channel mode a single channel is sampled and converted continuously The ADC results are written to the ADC12MEMx defined by the CSTARTADDx bits It is necessary to read the result after the c...

Страница 881: ...C12ENC ADC12ENC x pointer to ADC12MCTLx www ti com ADC12_B Operation 881 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated ADC12_B 34 2 8 4 Repeat Sequence of Channels Mode Repeated Autoscan Mode In repeat sequence of channels mode a sequence of channels is sampled and converted repeatedly This mode is also called repeated aut...

Страница 882: ...he end of the current conversion Reset ADC12ENC during a sequence or repeat sequence mode to stop the converter at the end of the current conversion Stop any conversion mode immediately by setting the CONSEQx 0 and resetting the ADC12ENC and ADC12ON bit Conversion data are unreliable NOTE No ADC12EOS bit set for sequence If no ADC12EOS bit is set and a sequence mode is selected resetting the ADC12...

Страница 883: ...egrated Temperature Sensor To use the on chip temperature sensor the user must enable the temperature sensor input channel by setting the ADC12TCMAP bit equal to 1 in the ADC12CTL3 register The user must then select the analog input channel ADC12INCHx 0x1E for the temperature sensor Any other configuration is done as if an external channel were selected including reference selection conversion mem...

Страница 884: ...ed to eliminate ground loops unwanted parasitic effects and noise Ground loops are formed when return current from the ADC flows through paths that are common with other analog or digital circuitry If care is not taken this current can generate small unwanted offset voltages that can add to or subtract from the reference or input voltages of the ADC The connections shown in Figure 34 13 prevent th...

Страница 885: ...ode See Section 11 2 11 for additional details The ADC12RDYIFG is set after the sample trigger is asserted when the ADC12_B local reference buffer is ready Note the ADC12RDYIFG will be set even when the ADC12B does not select the buffered reference It can be used during extended sample mode instead of adding the max ADC12_B local reference buffer settle time to the sample signal time 34 2 14 1 ADC...

Страница 886: ...ther ADC12_B interrupt is pending Interrupt handler for ADC12 INT_ADC12 Enter Interrupt Service Routine ADD ADC12IV PC Add offset to PC RETI Vector 0 No interrupt JMP ADOV Vector 2 ADC overflow JMP ADTOV Vector 4 ADC timing overflow JMP ADHI Vector 6 ADC12HIIFG JMP ADLO Vector 8 ADC12LOIFG JMP ADIN Vector A ADC12INIFG JMP ADM0 Vector C ADC12IFG0 Vectors E 70 JMP ADM30 Vector 72 ADC12IFG30 JMP ADRD...

Страница 887: ...C12CTL2_H Read write Byte 00h 06h ADC12CTL3 ADC12_B Control 3 Read write Byte 0000h Section 34 3 4 06h ADC12CTL3_L Read write Byte 00h 07h ADC12CTL3_H Read write 00h 08h ADC12LO ADC12_B Window Comparator Low Threshold Register Read write Word 0000h Section 34 3 8 08h ADC12LO_L Read write Byte 00h 09h ADC12LO_H Read write Byte 00h 0Ah ADC12HI ADC12_B Window Comparator High Threshold Register Read w...

Страница 888: ...L5 ADC12_B Memory Control 5 Read write Word 0000h Section 34 3 6 2Ah ADC12MCTL5_L Read write Byte 00h 2Bh ADC12MCTL5_H Read write Byte 00h 2Ch ADC12MCTL6 ADC12_B Memory Control 6 Read write Word 0000h Section 34 3 6 2Ch ADC12MCTL6_L Read write Byte 00h 2Dh ADC12MCTL6_H Read write Byte 00h 2Eh ADC12MCTL7 ADC12_B Memory Control 7 Read write Word 0000h Section 34 3 6 2Eh ADC12MCTL7_L Read write Byte ...

Страница 889: ... ADC12MCTL20 ADC12_B Memory Control 20 Read write Word 0000h Section 34 3 6 48h ADC12MCTL20_L Read write Byte 00h 49h ADC12MCTL20_H Read write Byte 00h 4Ah ADC12MCTL21 ADC12_B Memory Control 21 Read write Word 0000h Section 34 3 6 4Ah ADC12MCTL21_L Read write Byte 00h 4Bh ADC12MCTL21_H Read write Byte 00h 4Ch ADC12MCTL22 ADC12_B Memory Control 22 Read write Word 0000h Section 34 3 6 4Ch ADC12MCTL2...

Страница 890: ...EM3 ADC12_B Memory 3 Read write Word undefined Section 34 3 5 66h ADC12MEM3_L Read write Byte undefined 67h ADC12MEM3_H Read write Byte undefined 68h ADC12MEM4 ADC12_B Memory 4 Read write Word undefined Section 34 3 5 68h ADC12MEM4_L Read write Byte undefined 69h ADC12MEM4_H Read write Byte undefined 6Ah ADC12MEM5 ADC12_B Memory 5 Read write Word undefined Section 34 3 5 6Ah ADC12MEM5_L Read write...

Страница 891: ...EM18 ADC12_B Memory 18 Read write Word undefined Section 34 3 5 84h ADC12MEM18_L Read write Byte undefined 85h ADC12MEM18_H Read write Byte undefined 86h ADC12MEM19 ADC12_B Memory 19 Read write Word undefined Section 34 3 5 86h ADC12MEM19_L Read write Byte undefined 87h ADC12MEM19_H Read write Byte undefined 88h ADC12MEM20 ADC12_B Memory 20 Read write Word undefined Section 34 3 5 88h ADC12MEM20_L...

Страница 892: ...EM28 ADC12_B Memory 28 Read write Word undefined Section 34 3 5 98h ADC12MEM28_L Read write Byte undefined 99h ADC12MEM28_H Read write Byte undefined 9Ah ADC12MEM29 ADC12_B Memory 29 Read write Word undefined Section 34 3 5 9Ah ADC12MEM29_L Read write Byte undefined 9Bh ADC12MEM29_H Read write Byte undefined 9Ch ADC12MEM30 ADC12_B Memory 30 Read write Word undefined Section 34 3 5 9Ch ADC12MEM30_L...

Страница 893: ...nly when ADC12ENC 0 0000b 4 ADC12CLK cycles 0001b 8 ADC12CLK cycles 0010b 16 ADC12CLK cycles 0011b 32 ADC12CLK cycles 0100b 64 ADC12CLK cycles 0101b 96 ADC12CLK cycles 0110b 128 ADC12CLK cycles 0111b 192 ADC12CLK cycles 1000b 256 ADC12CLK cycles 1001b 384 ADC12CLK cycles 1010b 512 ADC12CLK cycles 1011b Reserved 1100b Reserved 1101b Reserved 1110b Reserved 1111b Reserved 11 8 ADC12SHT0x RW 0 ADC12_...

Страница 894: ...idence of the first rising edge of the SHI signal triggers the sampling timer but further sample and conversions are performed automatically as soon as the prior conversion is completed 6 5 Reserved R 0 Reserved Always reads as 0 4 ADC12ON RW 0 ADC12_B on Can be modified only when ADC12ENC 0 0b ADC12_B off 1b ADC12_B on 3 2 Reserved R 0 Reserved Always reads as 0 1 ADC12ENC RW 0 ADC12_B enable con...

Страница 895: ...le and hold source select 000b ADC12SC bit 001b see the device specific data sheet for source 010b see the device specific data sheet for source 011b see the device specific data sheet for source 100b see the device specific data sheet for source 101b see the device specific data sheet for source 110b see the device specific data sheet for source 111b see the device specific data sheet for source ...

Страница 896: ...EQx RW 0h ADC12_B conversion sequence mode select This bit should only be modified when ADC12ENC 0 except to stop a conversion immediately by setting ADC12CONSEQx 00 when ADC12ENC 1 00b Single channel single conversion 01b Sequence of channels 10b Repeat single channel 11b Repeat sequence of channels 0 ADC12BUSY R 0h ADC12_B busy This bit indicates an active sample or conversion operation 0b No op...

Страница 897: ...1b 10 bit 12 clock cycle conversion time 10b 12 bit 14 clock cycle conversion time 11b Reserved 3 ADC12DF RW 0h ADC12_B data read back format Data is always stored in the binary unsigned format 0b Binary unsigned Theoretically for ADC12DIF 0 and 12 bit mode the analog input voltage VREF results in 0000h the analog input voltage VREF results in 0FFFh 1b Signed binary 2s complement left aligned Theo...

Страница 898: ...r availability 9 ADC12ICH1MAP RW 0h Controls internal channel 1 selection to ADC input channel A28 Can be modified only when ADC12ENC 0 0b external pin is selected for ADC input channel A28 1b ADC input channel internal 1 is selected for ADC input channel A28 see device specific data sheet for availability 8 ADC12ICH0MAP RW 0h Controls internal channel 0 selection to ADC input channel A29 Can be m...

Страница 899: ...version Results RW undefined If ADC12DF 0 The 12 bit conversion results are right justified Bit 11 is the MSB Bits 15 12 are 0 in 12 bit mode bits 15 10 are 0 in 10 bit mode and bits 15 8 are 0 in 8 bit mode If the user writes to the conversion memory registers the results are corrupted If ADC12DF 1 The 12 bit conversion results are left justified 2s complement format Bit 15 is the MSB Bits 3 0 ar...

Страница 900: ...ifferential mode Can be modified only when ADC12ENC 0 0b Single ended mode enabled 1b Differential mode enabled 12 Reserved R 0h Reserved Always reads as 0 11 8 ADC12VRSEL RW 0h Selects combinations of VR and VR sources as well as the buffer selection Note there is only one buffer so it can be used for either VR or VR but not both Can be modified only when ADC12ENC 0 0000b VR AVCC VR AVSS 0001b VR...

Страница 901: ... Ain A10 Ain A11 01011b If ADC12DIF 0 A11 If ADC12DIF 1 Ain A10 Ain A11 01100b If ADC12DIF 0 A12 If ADC12DIF 1 Ain A12 Ain A13 01101b If ADC12DIF 0 A13 If ADC12DIF 1 Ain A12 Ain A13 01110b If ADC12DIF 0 A14 If ADC12DIF 1 Ain A14 Ain A15 01111b If ADC12DIF 0 A15 If ADC12DIF 1 Ain A14 Ain A15 10000b If ADC12DIF 0 A16 If ADC12DIF 1 Ain A16 Ain A17 10001b If ADC12DIF 0 A17 If ADC12DIF 1 Ain A16 Ain A1...

Страница 902: ...2 bit threshold value is left justified when ADC12DF 1 2s complement format Bit 15 is the MSB Bits 3 0 are 0 in 12 bit mode bits 5 0 are 0 in 10 bit mode and bits 7 0 are 0 in 8 bit mode 34 3 8 ADC12LO Register offset 08h reset 0000h ADC12_B Window Comparator Low Threshold Register Figure 34 21 ADC12LO Register 15 14 13 12 11 10 9 8 Low Threshold rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2...

Страница 903: ...upt request for ADC12IFG12 bit 0b Interrupt disabled 1b Interrupt enabled 11 ADC12IE11 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG11 bit 0b Interrupt disabled 1b Interrupt enabled 10 ADC12IE10 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG10 bit 0b Interrupt disabled 1b Interrupt enabled 9 ADC12IE9 RW 0h Interrupt enable Enables or d...

Страница 904: ...e Reset Description 2 ADC12IE2 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG2 bit 0b Interrupt disabled 1b Interrupt enabled 1 ADC12IE1 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG1 bit 0b Interrupt disabled 1b Interrupt enabled 0 ADC12IE0 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG0 bit 0b Interrupt...

Страница 905: ...t request for ADC12IFG28 bit 0b Interrupt disabled 1b Interrupt enabled 11 ADC12IE27 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG27 bit 0b Interrupt disabled 1b Interrupt enabled 10 ADC12IE26 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG26 bit 0b Interrupt disabled 1b Interrupt enabled 9 ADC12IE25 RW 0h Interrupt enable Enables or di...

Страница 906: ...eset Description 2 ADC12IE18 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG18 bit 0b Interrupt disabled 1b Interrupt enabled 1 ADC12IE17 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG17 bit 0b Interrupt disabled 1b Interrupt enabled 0 ADC12IE16 RW 0h Interrupt enable Enables or disables the interrupt request for ADC12IFG16 bit 0b Interr...

Страница 907: ...nterrupt enable The GIE bit must also be set to enable the interrupt 0b Interrupt disabled 1b Interrupt enabled 4 ADC12OVIE RW 0h ADC12MEMx overflow interrupt enable The GIE bit must also be set to enable the interrupt 0b Interrupt disabled 1b Interrupt enabled 3 ADC12HIIE RW 0h Interrupt enable for the exceeding the upper limit interrupt of the window comparator for ADC12MEMx result register The ...

Страница 908: ...when ADC12MEM13 is loaded with a conversion result The ADC12IFG13 bit is reset if ADC12MEM13 is accessed or it can be reset with software 0b No interrupt pending 1b Interrupt pending 12 ADC12IFG12 RW 0h ADC12MEM12 interrupt flag This bit is set when ADC12MEM12 is loaded with a conversion result The ADC12IFG12 bit is reset if ADC12MEM12 is accessed or it can be reset with software 0b No interrupt p...

Страница 909: ...W 0h ADC12MEM4 interrupt flag This bit is set when ADC12MEM4 is loaded with a conversion result The ADC12IFG4 bit is reset if ADC12MEM4 is accessed or it can be reset with software 0b No interrupt pending 1b Interrupt pending 3 ADC12IFG3 RW 0h ADC12MEM3 interrupt flag This bit is set when ADC12MEM3 is loaded with a conversion result The ADC12IFG3 bit is reset if ADC12MEM3 is accessed or it can be ...

Страница 910: ...when ADC12MEM29 is loaded with a conversion result The ADC12IFG29 bit is reset if ADC12MEM29 is accessed or it can be reset with software 0b No interrupt pending 1b Interrupt pending 12 ADC12IFG28 RW 0h ADC12MEM28 interrupt flag This bit is set when ADC12MEM28 is loaded with a conversion result The ADC12IFG28 bit is reset if ADC12MEM28 is accessed or it can be reset with software 0b No interrupt p...

Страница 911: ... ADC12MEM20 interrupt flag This bit is set when ADC12MEM20 is loaded with a conversion result The ADC12IFG20 bit is reset if ADC12MEM20 is accessed or it can be reset with software 0b No interrupt pending 1b Interrupt pending 3 ADC12IFG19 RW 0h ADC12MEM19 interrupt flag This bit is set when ADC12MEM19 is loaded with a conversion result The ADC12IFG19 bit is reset if ADC12MEM19 is accessed or it ca...

Страница 912: ...f the sample trigger has not been asserted 0b No interrupt pending 1b Interrupt pending 5 ADC12TOVIFG RW 0h ADC12_B conversion time overflow interrupt flag 0b No interrupt pending 1b Interrupt pending 4 ADC12OVIFG RW 0h ADC12MEMx overflow interrupt flag 0b No interrupt pending 1b Interrupt pending 3 ADC12HIIFG RW 0h Interrupt flag for exceeding the upper limit interrupt of the window comparator fo...

Страница 913: ...0Eh Interrupt Source ADC12MEM1 interrupt flag Interrupt Flag ADC12IFG1 010h Interrupt Source ADC12MEM2 interrupt flag Interrupt Flag ADC12IFG2 012h Interrupt Source ADC12MEM3 interrupt flag Interrupt Flag ADC12IFG3 014h Interrupt Source ADC12MEM4 interrupt flag Interrupt Flag ADC12IFG4 016h Interrupt Source ADC12MEM5 interrupt flag Interrupt Flag ADC12IFG5 018h Interrupt Source ADC12MEM6 interrupt...

Страница 914: ...2 03Ah Interrupt Source ADC12MEM23 interrupt flag Interrupt Flag ADC12IFG23 03Ch Interrupt Source ADC12MEM24 interrupt flag Interrupt Flag ADC12IFG24 03Eh Interrupt Source ADC12MEM25 interrupt flag Interrupt Flag ADC12IFG25 040h Interrupt Source ADC12MEM26 interrupt flag Interrupt Flag ADC12IFG26 042h Interrupt Source ADC12MEM27 interrupt flag Interrupt Flag ADC12IFG27 044h Interrupt Source ADC12M...

Страница 915: ...P_E Module Chapter 35 SLAU367P October 2012 Revised April 2020 Comparator E COMP_E Module Comparator_E is an analog voltage comparator This chapter describes the Comparator_E Comparator_E supports general comparator functionality for up to 16 channels Topic Page 35 1 COMP_E Introduction 916 35 2 COMP_E Operation 917 35 3 COMP_E Registers 923 ...

Страница 916: ... module supports precision slope analog to digital conversions supply voltage supervision and monitoring of external analog signals Features of COMP_E include Inverting and noninverting terminal input multiplexer Software selectable RC filter for the comparator output Output provided to Timer_A capture input Software control of the port input buffer Interrupt capability Selectable reference voltag...

Страница 917: ...ins using the CEIPSELx and CEIMSELx bits The comparator terminal inputs can be controlled individually The CEIPSELx and CEIMSELx bits allow Application of an external signal to the V and V terminals of the comparator Application of an external current source for example a resistor to the V or V terminal of the comparator Mapping of both terminals of the internal multiplexer to the outside Internal...

Страница 918: ...u should be used as a sampling time With 3 Tau the sampling capacitor is charged to approximately 95 of the input signal s voltage level with 5 Tau it is charged to more than 99 and with 10 Tau the sampled voltage is sufficient for 12 bit accuracy 35 2 5 Output Filter The output of the comparator can be used with or without internal filtering When control bit CEF is set the output is filtered with...

Страница 919: ...ncorporated Comparator E COMP_E Module Figure 35 3 RC Filter Response at the Output of the Comparator 35 2 6 Reference Voltage Generator Figure 35 4 shows the Comparator_E reference generator block diagram Figure 35 4 Reference Generator Block Diagram The interrupt flags of the comparator and the comparator output are unchanged while the reference voltage from the shared reference is settling If C...

Страница 920: ... the input voltage is near the transition level of the gate Disabling the port pin buffer eliminates the parasitic current flow and therefore reduces overall current consumption The CEPDx bits when set disable the corresponding Px y input buffer see Figure 35 5 When current consumption is critical any Px y pin connected to analog signals should be disabled with the associated CEPDx bits Selecting ...

Страница 921: ...charges and discharges the capacitor through Rref One output discharges capacitor through Rmeas The terminal is connected to the positive terminal of the capacitor The terminal is connected to a reference level for example 0 25 VCC The output filter should be used to minimize switching noise CEOUT is used to gate a timer capturing capacitor discharge time More than one resistive element can be mea...

Страница 922: ... ref Vref1 VCC Nmeas Nref Rmeas Rref R R meas ref Nmeas Nref COMP_E Operation www ti com 922 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Comparator E COMP_E Module ...

Страница 923: ...e 35 1 COMP_E Registers Offset Acronym Register Name Type Access Reset Section 00h CECTL0 Comparator_E control register 0 Read write Word 0000h Section 35 3 1 02h CECTL1 Comparator_E control register 1 Read write Word 0000h Section 35 3 2 04h CECTL2 Comparator_E control register 2 Read write Word 0000h Section 35 3 3 06h CECTL3 Comparator_E control register 3 Read write Word 0000h Section 35 3 4 0...

Страница 924: ... enable for the terminal of the comparator 0b Selected analog input channel for V terminal is disabled 1b Selected analog input channel for V terminal is enabled The internal reference voltage is disabled for this channel 14 12 Reserved R 0h Reserved Reads as 0 11 8 CEIMSEL RW 0h Channel input selected for the terminal of the comparator if CEIMEN is set to 1 7 CEIPEN RW 0h Channel input enable for...

Страница 925: ...consumes no power 0b Off 1b On 9 8 CEPWRMD RW 0h Power mode 00b High speed mode 01b Normal mode 10b Ultra low power mode 11b Reserved 7 6 CEFDLY RW 0h Filter delay The filter delay can be selected in four steps See the device specific data sheet for details 00b Typical filter delay of approximately 450 ns 01b Typical filter delay of approximately 900 ns 10b Typical filter delay of approximately 18...

Страница 926: ...hared reference voltage input 10b 2 0 V is selected as shared reference voltage input 11b 2 5 V is selected as shared reference voltage input 12 8 CEREF1 RW 0h Reference resistor tap 1 This register defines the tap of the resistor string while CEOUT 1 7 6 CERS RW 0h Reference source This bit define if the reference voltage is derived from VCC or from the precise shared reference 00b No current is ...

Страница 927: ...is disabled 12 CEPD12 RW 0h Port disable These bits individually disable the input buffer for the pins of the port associated with Comparator_E The bit CEPD12 disables the port of the comparator channel 12 0b The input buffer is enabled 1b The input buffer is disabled 11 CEPD11 RW 0h Port disable These bits individually disable the input buffer for the pins of the port associated with Comparator_E...

Страница 928: ...ables the port of the comparator channel 4 0b The input buffer is enabled 1b The input buffer is disabled 3 CEPD3 RW 0h Port disable These bits individually disable the input buffer for the pins of the port associated with Comparator_E The bit CEPD3 disables the port of the comparator channel 3 0b The input buffer is enabled 1b The input buffer is disabled 2 CEPD2 RW 0h Port disable These bits ind...

Страница 929: ... Reserved Reads as 0 9 CEIIE RW 0h Comparator_E output interrupt enable inverted polarity 0b Interrupt is disabled 1b Interrupt is enabled 8 CEIE RW 0h Comparator_E output interrupt enable 0b Interrupt is disabled 1b Interrupt is enabled 7 5 Reserved R 0h Reserved Reads as 0 4 CERDYIFG RW 0h Comparator_E ready interrupt flag This bit is set if the Comparator_E reference sources are settled and the...

Страница 930: ...EIV Register Description Bit Field Type Reset Description 15 0 CEIV R 0h Comparator_E interrupt vector word register The interrupt vector register reflects only interrupt flags whose interrupt enable bit are set Reading the CEIV register clears the pending interrupt flag with the highest priority 00h No interrupt pending 02h Interrupt Source CEOUT interrupt Interrupt Flag CEIFG Interrupt Priority ...

Страница 931: ...ontroller Chapter 36 SLAU367P October 2012 Revised April 2020 LCD_C Controller The LCD_C controller drives static and 2 mux to 8 mux LCDs This chapter describes the LCD_C controller The differences between LCD_B and LCD_C are listed in Table 36 1 Topic Page 36 1 LCD_C Introduction 932 36 2 LCD_C Operation 934 36 3 LCD_C Registers 950 ...

Страница 932: ... V typical Contrast control by software Support for the following types of LCDs Static 2 mux 1 2 bias or 1 3 bias 3 mux 1 2 bias or 1 3 bias 4 mux 1 2 bias or 1 3 bias 5 mux 1 3 bias 6 mux 1 3 bias 7 mux 1 3 bias 8 mux 1 3 bias The differences between LCD_B and LCD_C are listed in Table 36 1 Table 36 1 Differences Between LCD_B and LCD_C Feature LCD_B LCD_C Supported types of LCDs Static 2 3 4 mux...

Страница 933: ...ing Memory Registers LCDBMx only static 2 to 4 mux LCD Memory Registers LCDMx 0 1 ACLK VLOCLK Analog Voltage Multiplexer V1 V2 V3 V4 VD VC VB VA V5 LCDDIVx LCDBLKPREx LCDBLKDIVx LCDSx LCDSON LCDLP LCDBLKMODx Blinking and Display Control Blinking Frequency Divider BLKCLK Timing Generator LCDDISP LCDCLRBM LCDCLRM LCDSSEL LCD EXTBIAS www ti com LCD_C Introduction 933 SLAU367P October 2012 Revised Apr...

Страница 934: ...eration of the LCD controller is discussed in the following sections 36 2 1 LCD Memory The LCD memory organization differs slightly depending on the mode Each memory bit corresponds to one LCD segment or is not used depending on the mode To turn on an LCD segment its corresponding memory bit is set The memory can also be accessed word wise using the even addresses starting at LCDM1 LCDM3 Setting t...

Страница 935: ...with 160 segments Figure 36 3 LCD Memory for 5 Mux to 8 Mux Mode Example for 160 Segments 36 2 2 LCD Timing Generation The LCD_C controller uses the fLCD signal from the integrated clock divider to generate the timing for common and segment lines With the LCDSSEL bit ACLK with a frequency between 30 kHz and 40 kHz or VLOCLK can be selected as clock source into the divider The fLCD frequency is sel...

Страница 936: ... not used depending on the multiplexing mode LCDMXx To enable blinking for a LCD segment its corresponding memory bit is set The blinking memory can also be accessed word wise using the even addresses starting at LCDBM1 LCDBM3 Setting the bit LCDCLRBM clears all blinking memory registers at the next frame boundary It is automatically reset after the registers are cleared 36 2 4 2 Blinking Frequenc...

Страница 937: ...the internal charge pump is used a 4 7 µF or larger capacitor must be connected between the LCDCAP pin and ground If no capacitor is connected and the charge pump is enabled the LCDNOCAPIFG interrupt flag is set and the charge pump is disabled to prevent damage to the device To reduce system noise the charge pump can be temporarily disabled It is disabled when LCDCPEN 0 and re enabled when LCDCPEN...

Страница 938: ...CD_C Operation www ti com 938 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 5 2 LCD Bias Generation The fractional LCD biasing voltages V2 to V5 can be generated internally or externally independent of the source for VLCD The bias generation block diagram for LCD_C static and 2 mux to 8 mux modes is s...

Страница 939: ...as shown in the left part of Figure 36 4 When using an external resistor divider R33 may serve as a switched VLCD output when VLCDEXT 0 This allows the power to the resistor ladder to be turned off which eliminates current consumption when the LCD is not used When VLCDEXT 1 R33 serves as a VLCD input The bias generator supports 1 2 biasing when LCD2B 1 and 1 3 biasing when LCD2B 0 In static mode t...

Страница 940: ...V2 V4 V5 0 333 0 471 1 414 A typical approach to determine the required VLCD is by equating VRMS OFF with a LCD threshold voltage provided by the LCD manufacturer for example when the LCD exhibits approximately 10 contrast Vth 10 VRMS OFF Vth 10 Using the values for VRMS OFF VLCD provided in the table results in VLCD Vth 10 VRMS OFF VLCD In the static mode a suitable choice is VLCD greater than or...

Страница 941: ...nterrupt is immediately generated after servicing the initial interrupt A write access to the LCDCIV register automatically resets all pending interrupt flags In addition all flags can be cleared by software The LCDNOCAPIFG indicates that no capacitor is present at the LCDCAP pin when the charge pump is enabled Setting the LCDNOCAPIE bit enables the interrupt The LCDBLKONIFG bit is set on the risi...

Страница 942: ...are overhead for different interrupt sources includes interrupt latency and return from interrupt cycles but not the task handling itself Interrupt handler for LCD_B interrupt flags LCDB_HND Interrupt latency 6 ADD LCDBIV PC Add offset to Jump table 3 RETI Vector 0 No interrupt 5 JMP LCDNOCAP_HND Vector 2 LCDNOCAPIFG 2 JMP LCDBLKON_HND Vector 4 LCDBLKONIFG 2 JMP LCDBLKOFF_HND Vector 6 LCDBLKOFFIFG...

Страница 943: ...n 943 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 8 Static Mode In static mode each MSP430 segment pin drives one LCD segment and one common line COM0 is used Figure 36 5 shows some example static waveforms Figure 36 5 Example Static Waveforms ...

Страница 944: ... ti com 944 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 9 2 Mux Mode In 2 mux mode each MSP430 segment pin drives two LCD segments and two common lines COM0 and COM1 are used Figure 36 6 shows some example 2 mux 1 2 bias waveforms Figure 36 6 Example 2 Mux Waveforms ...

Страница 945: ... Operation 945 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 10 3 Mux Mode In 3 mux mode each MSP430 segment pin drives three LCD segments and three common lines COM0 COM1 and COM2 are used Figure 36 7 shows some example 3 mux 1 3 bias waveforms Figure 36 7 Example 3 Mux Waveforms ...

Страница 946: ... www ti com 946 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 11 4 Mux Mode In 4 mux mode each MSP430 segment pin drives four LCD segments and four common lines COM0 COM1 COM2 and COM3 are used Figure 36 8 shows some example 4 mux 1 3 bias waveforms Figure 36 8 Example 4 Mux Waveforms ...

Страница 947: ..._C Operation 947 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 12 6 Mux Mode In 6 mux mode each MSP430 segment pin drives six LCD segments and six common lines COM0 COM1 COM2 COM3 COM4 and COM5 are used Figure 36 9 shows some example 6 mux 1 3 bias waveforms Figure 36 9 Example 6 Mux Waveforms ...

Страница 948: ...ion www ti com 948 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller 36 2 13 8 Mux Mode In 8 mux mode each MSP430 segment pin drives eight LCD segments and eight common lines COM0 through COM7 are used Figure 36 10 shows some example 8 mux 1 3 bias waveforms Figure 36 10 Example 8 Mux 1 3 Bias Waveforms LCDLP ...

Страница 949: ...pril 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller Figure 36 11 shows some example 8 mux 1 3 bias waveforms with LCDLP 1 With LCDLP 1 the voltage sequence compared to the non low power waveform is reshuffled that is all of the timeslots marked with in Figure 36 10 are grouped together The same principle applies to all mux modes Figure 36 11 ...

Страница 950: ...h Section 36 3 1 002h LCDCCTL1 LCD_C control 1 Read write 0000h Section 36 3 2 004h LCDCBLKCTL LCD_C blinking control Read write 0000h Section 36 3 3 006h LCDCMEMCTL LCD_C memory control Read write 0000h Section 36 3 4 008h LCDCVCTL LCD_C voltage control Read write 0000h Section 36 3 5 00Ah LCDCPCTL0 LCD_C port control 0 Read write 0000h Section 36 3 6 00Ch LCDCPCTL1 LCD_C port control 1 Read writ...

Страница 951: ...17 S16 Read write Unchanged 029h LCDM10 LCD memory 10 S19 S18 Read write Unchanged 02Ah LCDM11 LCD memory 11 S21 S20 Read write Unchanged 02Bh LCDM12 LCD memory 12 S23 S22 Read write Unchanged 02Ch LCDM13 LCD memory 13 S25 S24 Read write Unchanged 02Dh LCDM14 LCD memory 14 S27 S26 Read write Unchanged 02Eh LCDM15 LCD memory 15 S29 S28 Read write Unchanged 02Fh LCDM16 LCD memory 16 S31 S30 Read wri...

Страница 952: ...emory 9 Read write Unchanged 049h LCDBM10 LCD blinking memory 10 Read write Unchanged 04Ah LCDBM11 LCD blinking memory 11 Read write Unchanged 04Bh LCDBM12 LCD blinking memory 12 Read write Unchanged 04Ch LCDBM13 LCD blinking memory 13 Read write Unchanged 04Dh LCDBM14 LCD blinking memory 14 Read write Unchanged 04Eh LCDBM15 LCD blinking memory 15 Read write Unchanged 04Fh LCDBM16 LCD blinking mem...

Страница 953: ...LCD memory 17 S16 Read write Unchanged 031h LCDM18 LCD memory 18 S17 Read write Unchanged 032h LCDM19 LCD memory 19 S18 Read write Unchanged 033h LCDM20 LCD memory 20 S19 Read write Unchanged 034h LCDM21 LCD memory 21 S20 Read write Unchanged 035h LCDM22 LCD memory 22 S21 Read write Unchanged 036h LCDM23 LCD memory 23 S22 Read write Unchanged 037h LCDM24 LCD memory 24 S23 Read write Unchanged 038h...

Страница 954: ...6 S45 Read write Unchanged 04Eh LCDM47 LCD memory 47 S46 Read write Unchanged 04Fh LCDM48 LCD memory 48 S47 Read write Unchanged 050h LCDM49 LCD memory 49 S48 Read write Unchanged 051h LCDM50 LCD memory 50 S49 Read write Unchanged 052h LCDM51 LCD memory 51 S50 Read write Unchanged 053h LCDM52 LCD memory 52 S51 Read write Unchanged 054h Reserved 055h Reserved 056h Reserved 057h Reserved 058h Reserv...

Страница 955: ...h LCD frequency pre scaler Together with LCDDIVx the LCD frequency fLCD is calculated as fLCD fACLK VLO LCDDIVx 1 2LCDPREx 000b Divide by 1 001b Divide by 2 010b Divide by 4 011b Divide by 8 100b Divide by 16 101b Divide by 32 110b Reserved defaults to divide by 32 111b Reserved defaults to divide by 32 7 LCDSSEL RW 0h Clock source select for LCD and blinking frequency 0b ACLK 30 kHz to 40 kHz 1b ...

Страница 956: ...t Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated LCD_C Controller Table 36 8 LCDCCTL0 Register Description continued Bit Field Type Reset Description 0 LCDON RW 0h LCD on This bit turns the LCD_C module on or off 0b LCD_C module off 1b LCD_C module on ...

Страница 957: ...isabled 1b Interrupt enabled 9 LCDBLKOFFIE RW 0h LCD blinking interrupt enable segments switched off 0b Interrupt disabled 1b Interrupt enabled 8 LCDFRMIE RW 0h LCD frame interrupt enable 0b Interrupt disabled 1b Interrupt enabled 7 4 Reserved R 0h Reserved 3 LCDNOCAPIFG RW 0h No capacitance connected interrupt flag Set when charge pump is enabled but no capacitance is connected to LCDCAP pin 0b N...

Страница 958: ... fACLK VLO LCDBLKDIVx 1 29 LCDBLKPREx NOTE Should only be changed while LCDBLKMODx 00 000b Divide by 1 001b Divide by 2 010b Divide by 3 011b Divide by 4 100b Divide by 5 101b Divide by 6 110b Divide by 7 111b Divide by 8 4 2 LCDBLKPREx RW 0h Clock pre scaler for blinking frequency Together with LCDBLKDIVx the blinking frequency fBLINK is calculated as fBLINK fACLK VLO LCDBLKDIVx 1 29 LCDBLKPREx N...

Страница 959: ... has in 5 mux mode and above has no effect It s immediately reset again 0b Contents of blinking memory registers LCDBMx remain unchanged 1b Clear content of all blinking memory registers LCDBMx 1 LCDCLRM RW 0h Clear LCD memory Clears all LCD memory registers LCDMx The bit is automatically reset when the LCD memory is cleared 0b Contents of LCD memory registers LCDMx remain unchanged 1b Clear conte...

Страница 960: ... 2 17 VREF VLCDx 1 0 05 VREF 1111b If VLCDREFx 00 or 10 VLCD 2 60 V 15 1 0 06 V 3 44 V If VLCDREFx 01 or 11 VLCD 2 17 VREF 15 1 0 05 VREF 2 87 VREF 8 Reserved R 0h Reserved 7 LCDREXT RW 0h V2 to V4 voltage on external Rx3 pins This bit selects the external connections for voltages V2 to V4 with internal bias generation LCDEXTBIAS 0 The bit is don t care if external biasing is selected LCDEXTBIAS 1...

Страница 961: ...nally VLCDEXT 0 and VLCDx 0 or VLCDREFx 0 2 1 VLCDREFx RW 0h Charge pump reference select If LCDEXTBIAS 1 or LCDREXT 1 settings 01 10 and 11 are not supported the internal reference voltage is used instead NOTE Should be changed only while LCDON 0 00b Internal reference voltage 01b External reference voltage 10b Internal reference voltage switched to external pin LCDREF R13 11b Reserved defaults t...

Страница 962: ...anged only while LCDON 0 0b Multiplexed pins are port functions 1b Pins are LCD functions 36 3 7 LCDCPCTL1 Register LCD_C Port Control Register 1 NOTE Settings for LCDSx should be changed only while LCDON 0 Figure 36 18 LCDCPCTL1 Register 15 14 13 12 11 10 9 8 LCDS31 LCDS30 LCDS29 LCDS28 LCDS27 LCDS26 LCDS25 LCDS24 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 rw 0 7 6 5 4 3 2 1 0 LCDS23 LCDS22 LCDS21 LCDS20...

Страница 963: ...upporting a maximum of 320 segments LCDS47 is reserved if COM7 to COM1 are shared with segments If COM7 to COM1 are not shared with segments LCDS40 to LCDS47 are reserved This bit affects only pins with multiplexed functions Dedicated LCD pins are always LCD function NOTE Settings for LCDSx should be changed only while LCDON 0 0b Multiplexed pins are port functions 1b Pins are LCD functions 36 3 9...

Страница 964: ... 0b Synchronization disabled 1b Synchronization enabled 14 8 Reserved R 0h Reserved 7 0 LCDCPDISx RW 0h LCD charge pump disable number of implemented bits and connected function is device specific 0b Connected function cannot disable charge pump 1b Connected function can disable charge pump 36 3 11 LCDCIV Register LCD_C Interrupt Vector Register Figure 36 22 LCDCIV Register 15 14 13 12 11 10 9 8 L...

Страница 965: ... Interface ESI Chapter 37 SLAU367P October 2012 Revised April 2020 Extended Scan Interface ESI The Extended Scan Interface ESI peripheral automatically scans sensors and measures linear or rotational motion This document describes the Extended Scan interface Topic Page 37 1 ESI Introduction 966 37 2 ESI Operation 967 37 3 ESI Registers 993 ...

Страница 966: ...e machine TSM and the Timer_A Output Stage The analog front end stimulates the sensors senses the signal levels and converts them into their digital representation The digital representations of a measurement sequence are stored in the preprocessing unit The stored digital signals are passed into the processing state machine The processing state machine is used to analyze and count rotation or mot...

Страница 967: ...o analog front ends available in the ESI The analog front end AFE1 provides sensor excitation and sample and hold circuit for measurements The analog front end is automatically controlled by the timing state machine TSM according to the information in the timing state machine table Figure 37 2 shows the analog front end block diagram NOTE Timing State Machine Signals Throughout this chapter signal...

Страница 968: ...el is 00b Selected input channel is 01b Selected input channel is 10b Selected input channel is 11b or test cycle is in progress Hysteresis programmable with the two registers Hysteresis programmable with the two registers Hysteresis programmable with the two registers Hysteresis programmable with the two registers AVCC 8 MSB 4 LSB en en ESI Operation www ti com 968 SLAU367P October 2012 Revised A...

Страница 969: ...istor dividers The excitation circuitry is shown in Figure 37 4 for one LC sensor connected When the ESITEN bit is set and the ESISH bit is cleared the excitation circuitry is enabled and the sample and hold circuitry is disabled When the ESIEX tsm signal from the timing state machine is high the ESICHx input of the selected channel is connected to ground ESIDVSS pin and the ESICOM input is connec...

Страница 970: ...tage Generator The mid voltage generator is on when ESIVMIDEN 1 and allows the LC sensors to oscillate freely The mid voltage generator requires a maximum of 6 ms to settle and requires ACLK to be active and operating at 32768 Hz 37 2 1 3 Sample And Hold Note that the sample and hold circuit is only available in the analog front end AFE1 The sample and hold is used to sample the sensor voltage to ...

Страница 971: ...log Input Equivalent Circuit The resistance of the source RS and Ri ESICHx affect tsample Equation 18 can be used to calculate the minimum sampling time tsample for a 12 bit conversion tsample RS RiESICHx ln 213 CSHC ESICHx 18 Substituting the values for RiESICHx and CSHC ESICHx given above the equation becomes tsample RS 3k 9 011 9 pF 19 For example if RS is 10 kΩ tsamplemust be greater than 1054...

Страница 972: ...bit is ESITCHOUT1 When AFE1 s ESICA1X 1 the ESICSEL and ESICI3 bits select between the ESICIx channels and the ESICI input allowing storage of the comparator output for one input signal into the four output bits ESIOUT0 to ESIOUT3 This can be used to observe the envelope function of sensors The output logic is enabled by the ESIRSON tsm signal When a comparator output is high while ESIRSON 1 an in...

Страница 973: ...C tsm control bits For each input there are two DAC registers to set the reference level as listed in Table 37 3 Together with the last stored output of the comparator ESIOUTx the two levels can be used as an analog hysteresis as shown in Figure 37 7 The individual settings for the four inputs can be used to compensate for mismatches between the sensors Table 37 3 Selected DAC Registers Analog Fro...

Страница 974: ...ements see device specific data sheet ESICA 1 ESICAAZ 1 ESITSM7 ESICA TSM_State7 normal comparator operation settle comparator ESICA 1 ESICAAZ 0 ESITSM8 ESICA TSM_State8 normal comparator operation processing of comparator output signal ESICA 1 ESICAAZ 0 37 2 2 ESI Timing State Machine The TSM is a sequential state machine that cycles through the ESITSMx registers and controls the analog front end...

Страница 975: ... ESICLK SMCLK ESITSM1 ESITSM30 ESIEN ESITSMRP ESIHFSEL SMCLK ESIOSC ESICNT3 Out Enable ESILFCLK ESIHFCLK ESICLKGON ESIHFSEL ESIDIV2x ESIDIV1x 0 1 Divider 1 2 4 8 Divider 1 2 4 8 ESIDIV3Ax Divider 2 450 3 3 6 ESICLKFQx ESITSMTRG 00 01 10 11 0 ESISTART ESIOSCCLK ACLK TSM clock 0 1 request TSM sequence is in progress rst As Ds www ti com ESI Operation 975 SLAU367P October 2012 Revised April 2020 Subm...

Страница 976: ...trol registers ESITSM2 to ESITSM31 The ESISTOP tsm control bit ensures that a user defined TSM sequence is terminated and the TSM progressing is switching into idle mode awaiting the next start trigger 37 2 2 2 TSM Idle Condition Selectable With ESITSM0 ESITSM0 register is used for two different tasks First by definition ESITSM0 register is always the first ESITSMx register within a TSM sequence T...

Страница 977: ...or parameters The TSM internal oscillator frequency can be measured with ACLK When ESIHFSEL 1 and ESICLKGON 1 ESICNT3 is reset and beginning with the next rising edge of ACLK ESICNT3 counts the clock cycles of the internal oscillator ESICNT3 counts the internal oscillator cycles for one ACLK period Reading ESICNT3 while it is counting will result in reading 01h The ACLK is automatically turned on ...

Страница 978: ... Incorporated Extended Scan Interface ESI Figure 37 9 Test Cycle Insertion 37 2 2 8 TSM Example Figure 37 10 shows an example for a TSM sequence The TSMx register values for the example are shown in Table 37 6 ACLK and ESIHFCLK are not drawn to scale The TSM sequence starts with ESITSM0 and ends with a set ESISTOP bit in ESITSM9 Only the ESITSM5 to ESITSM9 states are shown Table 37 6 TSM Example R...

Страница 979: ...er than configured by the ESIREPEATx bits Figure 37 10 Timing State Machine Example 37 2 3 ESI Pre Processing and State Storage The Pre Processing Unit PPU stores the measurement results of a TSM sequence Beside this it also allows to select up to three signals that are processed by the Processing State Machine PSM Up to four regular measurements and two test insertion measurements could sequentia...

Страница 980: ...t 37 2 4 TimerA Output Stage The comparator output of the analog front end AFE1 the ESIEX tsm signal and two preprocessing unit outputs PPUS1 and PPUS2 are connected to a Timer_A s capture inputs through the ESI s Timer_A output stage shown in Figure 37 12 There are two different modes that are selected by the ESICS bit The Timer_A Output Stage provides the ESIOx signals to one of the device s Tim...

Страница 981: ...1 the ESIEX tsm signal and the output bits PPUS1 and PPUS2 from the PPU can be selected as inputs to Timer_A This can be used to measure the duty cycle of PPUS1 or PPUS2 37 2 5 ESI Processing State Machine The PSM is a programmable state machine used to determine rotation and direction with its state table stored within the ESI memory ESI RAM The processing state machine measures rotation and cont...

Страница 982: ... single TSM sequence 37 2 5 2 ESI RAM The purpose of the ESI RAM is to store the user defined PSM table The ESI RAM can be accessed by PSM or CPU CPU write and read access to ESI RAM is only possible when ESI is disabled ESIEN 0 Any CPU write access to ESI RAM is ignored while ESI is active ESIEN 1 A CPU read access to ESI RAM is not possible while ESI is active in this case the CPU would read a 0...

Страница 983: ... a state where bit Q1 is set In case both bits Q1 and Q2 are set on a state transition ESICNT1 does not increment or decrement ESICNT2 decrements based on Q2 When ESICNT2EN 1 ESICNT2 decrements on a transition to a state where bit Q2 is set On the first count after a reset ESICNT2 will roll over from zero to 65535 0FFFFh When the next state is calculated to be the same state as the current state t...

Страница 984: ...state table Figure 37 14 Simplest PSM State Diagram ESIV2SEL 1 Simplest State Machine Example SIMPLEST_PSM db 000h State 00 State Table Index 0 db 000h State 01 State Table Index 1 db 000h State 10 State Table Index 2 db 002h State 11 State Table Index 3 If the PSM is in state 01 of the simplest state machine and the PSM has loaded the corresponding byte at index 01h of the state table Q7 Q6 Q5 Q4...

Страница 985: ...T3 outputs selected with the ESIIFGSET1x bits ESIIFG1 ESIIFG1 is set by the rising edge of the ESISTOP tsm signal ESIIFG2 ESIIFG2 is set at the start of a TSM sequence ESIIFG3 ESIIFG3 is set at different count intervals of the ESICNT1 counter selected with the ESITHR1 and ESITHR2 registers ESIIFG4 ESIIFG4 is set at different count intervals of the ESICNT2 counter selected with the ESIIS2x bits ESI...

Страница 986: ...nitial interrupt For example if the ESICNT1 ESIIFG3 and ESICNT2 ESIIFG4 interrupt flags are set when the interrupt service routine accesses the ESIIV register ESIIFG3 is reset automatically After the RETI instruction of the interrupt service routine is executed the ESIIFG4 interrupt flag generates another interrupt A write access to the ESIIV register clears all pending ESI interrupt flags 37 2 8 ...

Страница 987: ... above a reference level The DAC is used to set the reference level for the comparator and the comparator detects if the LC sensor oscillations are above or below the reference level If the oscillations are above the reference level the comparator will output a pulse train corresponding to the oscillations and the selected AFE output bit will 1 The measurement timing and reference level depend on ...

Страница 988: ...he DAC is used to set the reference level for the comparator and the comparator detects if the oscillation envelop is above or below the reference level The comparator and AFE outputs are connected to Timer_A and the capture compare registers for Timer_A are used to time the decay of the oscillation envelope The PSM is not used for the envelope test When the sensors are connected to the individual...

Страница 989: ...0 nF ESICOM ESICH1 ESICH0 ESICH2 ESICH3 ESIDVCC 0 1k www ti com ESI Operation 989 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Extended Scan Interface ESI Figure 37 18 LC Sensor Connections For the Envelope Test ...

Страница 990: ...otation is measured with resistive sensors by connecting the resistor dividers to ground for a short time allowing current flow through the dividers The resistors are affected by the rotating disc creating different divider voltages The divider voltages are sampled with the sample and hold circuits After the signals have settled the dividers may be switched off to prevent current flow and reduce p...

Страница 991: ...s and a quadrature encoded signal waveform Figure 37 20 Sensor Position and Quadrature Signals S1 PPUS1 S2 PPUS2 Quadrature decoding requires knowing the previous quadrature pair S1 PPUS1 and S2 PPUS2 as well as the current pair Comparing these two pairs will tell the direction of the rotation For example if the current pair is 00 it can change to 01 or 10 depending on direction Any other change i...

Страница 992: ... 1 Current Quadrature Pair 00 00 No Rotation 0 0 0 0 0 000h 00 01 Turns right 1 0 0 1 0 1 003h 00 10 Turns left 1 0 1 0 1 0 00Ch 00 11 Error 1 0 0 1 1 049h 01 00 Turns left 0 0 0 0 0 000h 01 01 No rotation 0 0 0 0 1 001h 01 10 Error 1 0 0 1 0 048h 01 11 Turns right 0 0 0 1 1 009h 10 00 Turns right 0 0 0 0 0 000h 10 01 Error 1 0 0 0 1 041h 10 10 No rotation 0 0 0 1 0 008h 10 11 Turns left 0 0 0 1 1...

Страница 993: ...rved 1Ah ESIIV ESI interrupt vector Read Word Reset with PUC 1Ch ESIINT1 ESI interrupt register 1 Read Write Word Reset with PUC 1Eh ESIINT2 ESI interrupt register 2 Read Write Word Reset with PUC 20h ESIAFE ESI AFE control register Read Write Word Reset with PUC 22h ESIPPU ESI PPU control register Read Write Word Reset with PUC 24h ESITSM ESI TSM control register Read Write Word Reset with PUC 26...

Страница 994: ... Register Extended Scan Interface Debug Register 2 Figure 37 23 ESIDEBUG2 Register 15 14 13 12 11 10 9 8 Unused TSM_Index r r r r r r r r 7 6 5 4 3 2 1 0 PSM_Bits r r r r r r r r Table 37 11 ESIDEBUG2 Register Description Bit Field Type Reset Description 15 13 Unused R 0h Unused These bits are always read as zero 12 8 TSM_Index R 0h These bits show the TSM register pointer index 7 0 PSM_Bits R 0h ...

Страница 995: ... zero 14 12 DAC1_Register R 0h These bits show which DAC1 register is currently selected to control the DAC1 11 0 DAC1_Data R 0h These bits show value of the currently selected DAC1 register 37 3 5 ESIDEBUG5 Register Extended Scan Interface Debug Register 5 Figure 37 26 ESIDEBUG5 Register 15 14 13 12 11 10 9 8 Unused DAC2_Register DAC2_Data r r r r r r r r 7 6 5 4 3 2 1 0 DAC2_Data r r r r r r r r...

Страница 996: ...r 0 Table 37 15 ESICNT0 Register Description Bit Field Type Reset Description 15 0 ESICNT0x R 0h ESICNT0 These bits are the ESICNT0 counter ESICNT0 is reset when ESIEN 0 or when ESICNT0RST 1 37 3 7 ESICNT1 Register Extended Scan Interface Counter 1 Register Figure 37 28 ESICNT1 Register 15 14 13 12 11 10 9 8 ESICNT1x r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 ESICNT1x r 0 r 0 r 0 r 0 r 0 r 0 ...

Страница 997: ...Description 15 0 ESICNT2x R 0h ESICNT2 These bits are the ESICNT2 counter ESICNT2 is reset when ESIEN 0 or when ESICNT2RST 1 37 3 9 ESICNT3 Register Extended Scan Interface Oscillator Counter Register Figure 37 30 ESICNT3 Register 15 14 13 12 11 10 9 8 ESICNT3x r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 7 6 5 4 3 2 1 0 ESICNT3x r 0 r 0 r 0 r 0 r 0 r 0 r 0 r 0 Table 37 18 ESICNT3 Register Description Bit Fiel...

Страница 998: ...source Writing to this register clears all pending Extended Scan Interface interrupt flags 00h No interrupt pending 02h Interrupt Source Rising edge of the ESISTOP tsm signal Interrupt Flag ESIIFG1 Interrupt Priority Highest 04h Interrupt Source ESIOUT0 to ESIOUT3 conditions selected by ESIIFGSETx bits Interrupt Flag ESIIFG0 06h Interrupt Source ESIOUT4 to ESIOUT7 conditions selected by ESIIFGSET2...

Страница 999: ...G0 is set when ESIOUT1 is set 011b ESIIFG0 is set when ESIOUT1 is reset 100b ESIIFG0 is set when ESIOUT2 is set 101b ESIIFG0 is set when ESIOUT2 is reset 110b ESIIFG0 is set when ESIOUT3 is set 111b ESIIFG0 is set when ESIOUT3 is reset 9 Reserved R 0h Reserved This bit is always read as zero and when written does not affect the bit setting 8 ESIIE8 RW 0h Interrupt enable These bits enable or disab...

Страница 1000: ... the ESIIFG3 bit descriptions see control register ESIINT2 0b Interrupt disabled 1b Interrupt enabled 2 ESIIE2 RW 0h Interrupt enable These bits enable or disable the interrupt request for the ESIIFG2 bit Details about the interrupt functionality can be found in the ESIIFG2 bit descriptions see control register ESIINT2 0b Interrupt disabled 1b Interrupt enabled 1 ESIIE1 RW 0h Interrupt enable Thes...

Страница 1001: ...4 0 10b ESIIFG7 is set if ESICNT0 modulo 256 0 11b ESIIFG7 is set when ESICNT0 increments from FFFFh to 00h 9 Reserved R 0h Reserved This bit is always read as zero and when written does not affect the bit setting 8 ESIIFG8 RW 0h ESIIFG8 is set by one of the AFE2 s ESIOUTx outputs selected with the ESIIFGSET2x bits 0b No interrupt pending 1b Interrupt pending 7 ESIIFG7 RW 0h ESI interrupt flag 7 E...

Страница 1002: ...enerated by the divided ACLK A TSM sequence started with ESISTART bit does not set ESIIFG2 ESIIFG2 must be reset with software 0b No interrupt pending 1b Interrupt pending 1 ESIIFG1 RW 0h ESI interrupt flag 1 This bit is set by the rising edge of the ESISTOP tsm signal ESIIFG1 must be reset with software 0b No interrupt pending 1b Interrupt pending 0 ESIIFG0 RW 0h ESI interrupt flag 0 This bit is ...

Страница 1003: ...trolled by ESICA tsm bit 9 ESICA2INV RW 0h Invert AFE2 s comparator output 0b Comparator output in AFE2 is not inverted 1b Comparator output in AFE2 is inverted 8 ESICA1INV RW 0h Invert AFE1 s comparator output 0b Comparator output in AFE1 is not inverted 1b Comparator output in AFE1 is inverted 7 ESICA2X RW 0h AFE2 s comparator input select This bit selects groups of signals for the comparator in...

Страница 1004: ...d to ESIVMIDEN to avoid confusion with supply pin naming 3 ESISHTSM 1 RW 0h Sample and hold ESIDVSS select 0b The ground connection of the sample capacitor is connected to ESIDVSS regardless of the TSM control 1b The ground connection of the sample capacitor is controlled by the TSM 2 ESIVMIDEN 2 RW 0h Mid voltage generator 0b AVCC 2 generator is off 1b AVCC 2 generator is on if ESISH 0 1 ESISH RW...

Страница 1005: ...ays read as zero and when written do not affect the bit setting 9 ESITCHOUT1 R 0h Latched AFE1 comparator output for test channel 1 8 ESITCHOUT0 R 0h Latched AFE1 comparator output for test channel 0 7 ESIOUT7 R 0h Latched AFE2 comparator output when ESICH3 input is selected 6 ESIOUT6 R 0h Latched AFE2 comparator output when ESICH2 input is selected 5 ESIOUT5 R 0h Latched AFE2 comparator output wh...

Страница 1006: ...trigger 10b Software trigger for TSM When ESISTART bit is set by software a TSM start trigger is generated Note that for this setting an ACLK synchronization sequence is performed that takes up to 2 5 ACLK cycles 11b Either the ACLK divider ESIDIV3Ax and ESIDIV3Bx or the ESISTART bit is used for TSM start trigger 11 ESISTART RW 0h TSM software start trigger In case the ESISTART bit is selected for...

Страница 1007: ...ivision for the TSM 00b 1 01b 2 10b 4 11b 8 Table 37 25 TSM Start Trigger ACLK Divider ACLK Divider ESIDIV3Bx ESIDIV3Ax ACLK Divider ESIDIV3Bx ESIDIV3Ax 2 000 000 126 011 100 6 000 001 130 010 110 10 000 010 150 010 111 14 000 011 154 011 101 18 000 100 162 100 100 22 000 101 182 011 110 26 000 110 198 100 101 30 000 111 210 011 111 42 001 011 234 100 110 50 010 010 242 101 101 54 001 100 270 100 ...

Страница 1008: ... Reserved These bits are always read as zero and when written do not affect the bit setting 9 8 ESITEST4SEL RW 0h Output signal selection for ESITEST4 pin 00b Q2 signal from PSM table 01b Q1 signal from PSM table 10b TSM clock signal from Timing State Machine 11b AFE1 s comparator output signal ESIC1OUT 7 ESIV2SEL RW 1h Source Selection for V2 bit of Next State Latch 0b PPUS3 signal is used for V2...

Страница 1009: ...hese bits are used to adjust the internal oscillator frequency Each increase or decrease of the ESICLKFQx bits increases or decreases the internal oscillator frequency by approximately 3 000000b Minimum frequency 100000b Nominal frequency 111111b Maximum frequency 7 2 Reserved R 0h Reserved These bits are always read as zero and when written do not affect the bit setting 1 ESICLKGON RW 0h Internal...

Страница 1010: ...S2SELx RW 0h PPUS2 source select These bits select the PPUS2 source for the PSM 000b ESIOUT0 is the PPUS2 source 001b ESIOUT1 is the PPUS2 source 010b ESIOUT2 is the PPUS2 source 011b ESIOUT3 is the PPUS2 source 100b ESIOUT4 is the PPUS2 source 101b ESIOUT5 is the PPUS2 source 110b ESIOUT6 is the PPUS2 source 111b ESIOUT7 is the PPUS2 source 9 7 ESIS1SELx RW 0h PPUS1 source select These bits selec...

Страница 1011: ...3 when ESICAX 1 2 ESICS RW 0h Comparator output ir Timer_A input selection 0b The ESIEX tsm signal and the comparator output are connected to the TACCRx inputs 1b The ESIEX tsm signal and the ESIOUTx outputs are connected to the TACCRx inputs selected with the ESIS1SELx and ESIS2SELx bits PPUS1 and PPUS2 signals 1 ESITESTD RW 0h Test cycle insertion Setting this bit inserts a test cycle between TS...

Страница 1012: ... 15 0 Threshold1 RW 0h Threshold for ESICNT1 counter The interrupt flag ESIIFG3 is set when ESICNT1 content and Threshold 1 is equal for example used to detect a certain increase of ESICNT1 37 3 20 ESITHR2 Register ESI PSM Counter Threshold 2 Register Figure 37 41 ESITHR2 Register 15 14 13 12 11 10 9 8 Threshold2 rw 1 rw 1 rw 1 rw 1 rw 1 rw 1 rw 1 rw 1 7 6 5 4 3 2 1 0 Threshold2 rw 1 rw 1 rw 1 rw ...

Страница 1013: ...escription Bit Field Type Reset Description 15 12 Reserved R 0h Reserved These bits are always read as zero and when written do not affect the bit setting 11 0 DAC_Data RW 0h 12 bit DAC data 37 3 22 ESIDAC2Rx Register x 0 to 7 Extended Scan Interface Digital To Analog Converter 2 Register x x 0 to 7 Figure 37 43 ESIDAC2Rx Register 15 14 13 12 11 10 9 8 Reserved DAC_Data r0 r0 r0 r0 rw rw rw rw 7 6...

Страница 1014: ...ycles for this state The number of clock cycles ESIREPEATx 1 Note that all ESIREPEATx bits should be cleared within the ESITSMx state that generates the end of sequence ESISTOP bit is set 10 ESICLK RW 0h This bit selects the clock source for the TSM 0b The TSM clock source is the high frequency source selected by the ESIHFSEL bit 1b The TSM clock source is ACLK 9 ESISTOP RW 0h This bit indicates t...

Страница 1015: ...utozero The length for autozero is adjusted by the selected clock ESICLK and the programmed repeat cycles ESIREPEATx See device specific data sheet for appropriate timing requirements 4 ESICA RW 0h TSM comparator on Setting this bit turns the AFE1 comparator and optionally the AFE2 comparator on for this state 0b AFE1 comparator and AFE2 comparator are off during this state 1b AFE1 comparator is o...

Страница 1016: ...ry Description Bit Field Type Reset Description 7 Q7 When Q7 1 ESIIFG6 will be set When ESIQ6EN 1 and ESIQ7EN 1 and Q7 1 the PSM proceeds to the next state immediately regardless of the ESISTOP tsm signal and Q7 is used in the next state calculation 6 Q6 When Q6 1 ESIIFG5 will be set When ESIQ6EN 1 Q6 will be used in the next state calculation 5 Q5 Bit 5 of the next state 4 Q4 Bit 4 of the next st...

Страница 1017: ... Embedded Emulation Module EEM Chapter 38 SLAU367P October 2012 Revised April 2020 Embedded Emulation Module EEM This chapter describes the embedded emulation module EEM that is implemented in all devices Topic Page 38 1 Embedded Emulation Module EEM Introduction 1018 38 2 EEM Building Blocks 1020 38 3 EEM Configurations 1021 ...

Страница 1018: ...ddress bus MAB or memory data bus MDB Up to two device dependent hardware triggers or breakpoints on CPU register write accesses MAB MDB and CPU register access triggers can be combined to form up to ten device dependent complex triggers or breakpoints Up to two device dependent cycle counters Trigger sequencing device dependent Storage of internal bus and control signals using an integrated trace...

Страница 1019: ... 5 6 7 8 9 Start or Stop Cycle Counter Start or Stop State Storage OR OR OR www ti com Embedded Emulation Module EEM Introduction 1019 SLAU367P October 2012 Revised April 2020 Submit Documentation Feedback Copyright 2012 2020 Texas Instruments Incorporated Embedded Emulation Module EEM Figure 38 1 Large Implementation of EEM ...

Страница 1020: ...e what is written into a selected register with a given value The observed register can be selected for each trigger independently The comparison can be or The comparison can also be limited to certain bits with the use of a bit mask Both types of triggers can be combined to form more complex triggers For example a complex trigger can signal when a particular value is written into a user specified...

Страница 1021: ...e debug mode the entry and wakeup times to and from low power modes may be different compared to normal operation application mode NOTE Pay careful attention to the real time behavior when using low power modes with the device connected to a development tool There are two different debug modes available the default debug mode and a ultra low power debug mode See Code Composer Studio IDE for MSP430...

Страница 1022: ...e 3 Four upper addr bits All 16 or 20 bits CPU register write triggers 0 1 1 2 Combination triggers 2 4 6 10 Sequencer No No Yes Yes State storage No No No Yes Cycle counter 1 1 1 2 including triggered start or stop In general the following features can be found on any device At least two MAB or MDB triggers supporting Distinction between CPU DMA read and write accesses or comparison in XS only At...

Страница 1023: ... description sections with Section 12 4 1 PxIV Register 388 Updated a link and description in Section 17 2 3 Where to Start 449 Removed WDTCTL_L and WDTCTL_H registers because any read or write access must use word instructions 640 Changed the offset of the WDTCTL register in Table 24 1 WDT_A Registers to match base address in data sheets 640 Changed the step Adjust the frequency the example that ...

Страница 1024: ...se resources are subject to change without notice TI grants you permission to use these resources only for development of an application that uses the TI products described in the resource Other reproduction and display of these resources is prohibited No license is granted to any other TI intellectual property right or to any third party intellectual property right TI disclaims responsibility for...

Отзывы:

Нет отзывов

Похожие инструкции для MSP430FR58 Series

Lantronix xPico 110 User Manual preview
xPico 110
Бренд: Lantronix Страницы: 17
Rohm BD7682FJ-LB-EVK-302 Quick Start Manual preview
BD7682FJ-LB-EVK-302
Бренд: Rohm Страницы: 5
JETWAY P4X400DM User Manual preview
P4X400DM
Бренд: JETWAY Страницы: 48
QMTECH XILINX SPARTAN-7 User Manual preview
XILINX SPARTAN-7
Бренд: QMTECH Страницы: 15
Diamond Systems Athena II User Manual preview
Athena II
Бренд: Diamond Systems Страницы: 112
Texas Instruments DAC63204EVM User Manual preview
DAC63204EVM
Бренд: Texas Instruments Страницы: 25
IEI Technology tKINO-AL-E1-R10 Quick Installation Manual preview
tKINO-AL-E1-R10
Бренд: IEI Technology Страницы: 12
ON Semiconductor NCV891234 User Manual preview
NCV891234
Бренд: ON Semiconductor Страницы: 8
JETWAY K8T8AS - REV 3.0 User Manual preview
K8T8AS - REV 3.0
Бренд: JETWAY Страницы: 26
Texas Instruments bq76925EVM User Manual preview
bq76925EVM
Бренд: Texas Instruments Страницы: 44
ASROCK IMB-390-D Settings Manual preview
IMB-390-D
Бренд: ASROCK Страницы: 2
Commell LE-37F User Manual preview
LE-37F
Бренд: Commell Страницы: 29
Intel EMB-H61A Manual preview
EMB-H61A
Бренд: Intel Страницы: 91
Supermicro MBD-X11SCH-F-O User Manual preview
MBD-X11SCH-F-O
Бренд: Supermicro Страницы: 119
AOpen MX46-800L Easy Installation Manual preview
MX46-800L
Бренд: AOpen Страницы: 8
TYAN S2505 User Manual preview
S2505
Бренд: TYAN Страницы: 54
TYAN S2498 Manual preview
S2498
Бренд: TYAN Страницы: 62
ASROCK PHANTOM GAMING B650E PG-ITX WiFi User Manual preview
PHANTOM GAMING B650E PG-ITX WiFi
Бренд: ASROCK Страницы: 62

Бренды по названию

Популярные бренды

Загрузить еще бренды