Mitsubishi MELFA CR1D Скачать руководство пользователя страница 128 | Manualshive

Страница: 128 / 458

background image

4-115

MELFA-BASIC V functions

4MELFA-BASIC V

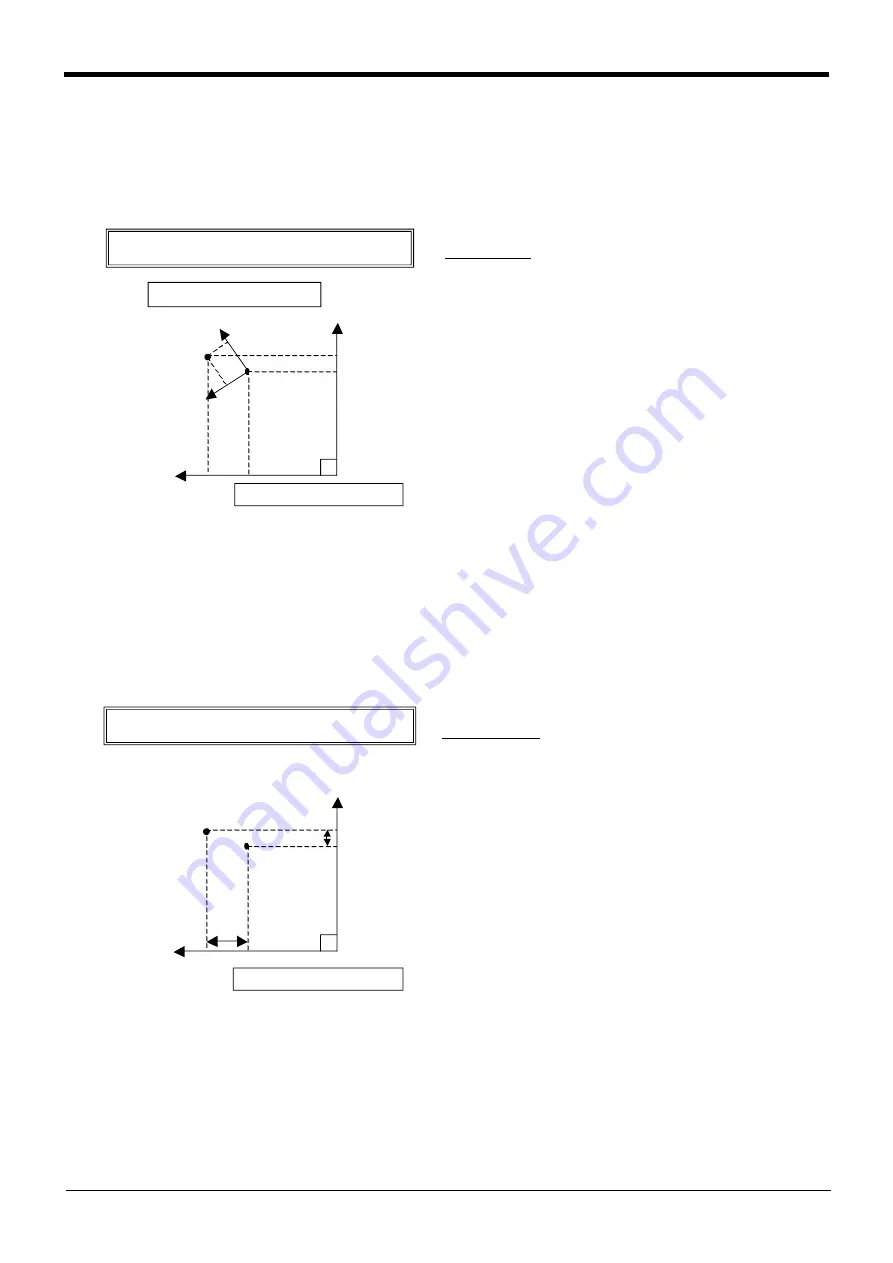
(2) Relative calculation of position data (multiplication)

Numerical variables are calculated by the usual four arithmetic operations. The calculation of position vari-
ables involves coordinate conversions, however, not just the four basic arithmetic operations. This is
explained using simple examples.

An example of relative calculation (multiplication)
1 P2=(10,5,0,0,0,0)(0,0)
2 P100=P1*P2
3 Mov P1
4 Mvs P100
P1=(200,150,100,0,0,45)(4,0)

In this example, the hand tip is moved relatively within the
P1 tool coordinate system at teaching position P1. The
values of the X and Y coordinates of P2 become the
amount of movement within the tool coordinate system.
The relative calculation is given by multiplication of the P
variables. Be aware that the result becomes different if the
order of multiplication is different. The variable that speci-
fies the amount of relative movement (P2) should be
entered lastly.
If the posture axis parts of P2 (A, B, and C) are 0, the pos-
ture of P1 is used as is. If there are non-zero values avail-
able, the new posture is determined by rotating the hand
around the Z, Y, and X axes (in the order of C, B, and A)
relative to the posture of P1. Multiplication corresponds to
addition within the tool coordinate system, while division
corresponds to subtraction within the tool coordinate sys-
tem.

(3) Relative calculation of position data (Addition)

An example of relative calculation(Addition)

1 P2=(5,10,0,0,0,0)(0,0)
2 P100=P1+P2
3 Mov P1
4 Mvs P100
P1=(200,150,100,0,0,45)(4,0)

In this example, the hand is moved relatively within the
robot coordinate system at teaching position P1. The val-
ues of the X and Y coordinates of P2 become the amount
of movement within the robot coordinate system. The rela-
tive calculation is given by addition of the P variables.
If a value is entered for the C-axis coordinate of P2, it is
possible to change the C-axis coordinate of P100. The
resulting value will be the sum of the C-axis coordinate of
P1 and the C-axis coordinate of P2.

CAUTION)
In the example above, the explanation is made in two dimensions for the sake of simplicity. In actuality, the
calculation is made in three dimensions. In addition, the tool coordinate system changes depending on the
posture.

X

Y

X1

Y1

P1

5mm

10mm

P100

M ultip lication b etween P variab les

(relative calculation in the tool coord inate system )

Tool coord inate system at P1

Rob ot coord inate system

X

Y

P1

P100

10mm

5mm

Ad d ition of P variab les

(relative calculation in the rob ot coord inate system )

Rob ot coord inate system

«
...
126
127
128
129
130
...
»

Содержание MELFA CR1D

Страница 1: ...Mitsubishi Industrial Robot CR1D CR2D CR3D Controller INSTRUCTION MANUAL Detailed explanations of functions and operations BFP A8661 A ...

Страница 2: ......

Страница 3: ...s on the start switch etc This also applies to maintenance work with the power source turned ON Indication of teaching work in progress Provide a fence or enclosure during operation to prevent contact of the operator and robot Installation of safety fence Establish a set signaling method to the related operators for starting work and follow this method Signaling of operation start As a principle t...

Страница 4: ...e this could lead to malfunctioning by noise or to electric shock accidents Indicate the operation state during robot operation Failure to indicate the state could lead to operators approaching the robot or to incorrect operation When carrying out teaching work in the robot s movement range always secure the priority right for the robot control Failure to observe this could lead to personal injuri...

Страница 5: ...y interfere with the peripheral device by drop or move by inertia of the arm Do not turn off the main power to the robot controller while rewriting the internal information of the robot controller such as the program or parameters If the main power to the robot controller is turned off while in automatic operation or rewriting the program or parameters the internal information of the robot control...

Страница 6: ...ies Please install the earth leakage breaker in the primary side supply power supply of the controller because of leakage protection 注意保護アース端子 PE 電源端子台漏電遮断器 NV 端子カバー端子カバーアース接続ネジコントローラ Controller Cover Cover earth leakage breaker Terminal Earth screw ...

Страница 7: ... pattern of the sequencer link was added The I O function of the sequencer link was added The connection method of display equipment GOT was added The communications parameter COMDEV etc and the communication setup were changed Continuing function was corrected parameter CTN The initial value of TB override operation rights parameter OvrdTB was changed The initial value of the dedicated I O parame...

Страница 8: ...3 23 3 2 9 Impact Detection during Jog Operation 3 24 1 Impact Detection Level Adjustment during Jog Operation 3 25 3 3 Opening Closing the Hands 3 26 3 4 Aligning the Hand 3 27 3 5 Programming 3 29 3 5 1 Creating a program 3 29 1 Opening the program edit screen 3 29 2 Creating a program 3 30 3 Completion of program creation and saving programs 3 32 4 Correcting a program 3 33 5 Registering the cu...

Страница 9: ...ke screen 3 76 1 Oorigin 3 76 2 Brake 3 76 3 16 Operation of setup initialization screen 3 78 1 Initialize the program 3 78 2 Initialize the parameter 3 79 3 Initialize the battery 3 80 4 Operation 3 81 5 Time setup 3 81 6 Version 3 82 3 17 Operation of the initial setting screen 3 83 1 Set the display language 3 83 2 Adjustment of contrast 3 85 4 MELFA BASIC V 4 87 4 1 MELFA BASIC V functions 4 8...

Страница 10: ...ultitask program 4 121 1 Starting the multitask 4 121 2 Display of operation status 4 121 4 2 6 Example of using multitask 4 122 1 Robot work details 4 122 2 Procedures to multitask execution 4 123 4 2 7 Program capacity 4 124 1 Program save area 4 124 2 Program edit area 4 124 3 Program execution area 4 124 4 3 Detailed specifications of MELFA BASIC V 4 126 1 Program name 4 126 2 Command statemen...

Страница 11: ...ority level of operations 4 151 4 9 Depth of program s control structure 4 151 4 10 Reserved words 4 151 4 11 Detailed explanation of command words 4 152 4 11 1 How to read the described items 4 152 4 11 2 Explanation of each command word 4 152 4 12 Detailed explanation of Robot Status Variable 4 264 4 12 1 How to Read Described items 4 264 4 12 2 Explanation of Each Robot Status Variable 4 264 4 ...

Страница 12: ...09 2 Robot CPU parameter setting 6 409 6 2 2 CPU shared memory and robot I O signal compatibility 6 411 6 2 3 Sequence ladder example 6 411 6 2 4 Assignment of the dedicated I O signal at factory shipping 6 413 6 2 5 Comparison of the I O point of the CRnQ700 and the CRn500 series 6 415 6 3 Dedicated input output 6 416 6 4 Enable disable status of signals 6 423 6 5 External signal timing chart 6 4...

Страница 13: ...Version P1 or later T B Version 1 0 or later No part of this manual may be reproduced by any means or in any form without prior consent from Mitsubishi The details of this manual are subject to change without notice An effort has been made to make full descriptions in this manual However if any discrepancies or unclear points are found please contact your dealer The information contained in this d...

Страница 14: ...re also explained Explains the procedures required to operate the robot arm unpacking transportation installation confirmation of operation and the maintenance and inspection procedures Explains the procedures required to operate the controller unpacking transportation installation confirmation of operation basic operation from creating the program to automatic operation and the maintenance and in...

Страница 15: ...s observe these precautions to safely use the robot Precaution indicating cases where operator could be subject to injury or physical damage could occur if handling is mistaken Always observe these precautions to safely use the robot JOG If a word is enclosed in brackets or a box in the text this refers to a key on the teaching pendant RESET EXE A B This indicates to press the B key while holding ...

Страница 16: ...ng work This also applies to maintenance work with the power source turned ON Setting of emergency stop switch During teaching work place a sign indicating that teaching work is in progress on the start switch etc This also applies to maintenance work with the power source turned ON Indication of teaching work in progress Provide a fence or enclosure during operation to prevent contact of the oper...

Страница 17: ...juries or damage if the object comes off or flies off during operation Securely ground the robot and controller Failure to observe this could lead to malfunctioning by noise or to electric shock accidents Indicate the operation state during robot operation Failure to indicate the state could lead to operators approaching the robot or to incorrect operation When carrying out teaching work in the ro...

Страница 18: ...tic operation or rewriting the program or parameters the internal information of the robot controller may be damaged When the SSCNETIII cable is removed install the cap in the connector If the cap is not installed there is a possibility of malfunctioning by adhesion of the dust etc Don t remove the SSCNETIII cable when the power supply of the robot controller is turned on Don t face squarely the l...

Страница 19: ...ay panel The alarm No program No override value etc are displayed MODE key switch This changes the robot s operation mode AUTOMATIC operations from the controller or external equipment are valid Operations for which the operation mode must be at the external device or T B are not possible It is necessary to set the parameter for the rights of operation to connection between the operation panel and...

Страница 20: ...e right of operation Opeertion panel External signal Teaching pendant No right of operation DOWN UP Maker information Mecha name Serial number S W version Battery remaining time Temperature Maker message DOWN UP 1 1 The user message displays the character string alphanumeric character of a maximum of the 32 characters set as USERMEG It can be used as the name and version name of the application pr...

Страница 21: ... status displays The various states are indicated by the character at left end Override Program name Battery remaining time Temperature High level error Low level error Warning O P operation rights If the operation panel has the right of operation the upper left dot turns on ...

Страница 22: ...OP key This stops the program and decelerates the robot to a stop 9 OVRD OVRD key Change moving speed Speed goes up by OVRD key Speed goes down by OVRD key 10 JOG operation key Move the robot according to jog mode And input the numerical value 11 SERVO key Press this key with holding AA key lightly then servo power will turn on 12 MONITOR key It becomes monitor mode and display the monitor menu 13...

Страница 23: ...MANUAL Operation rights T B X X XNote 2 Controller operation panel Note 1 X XNote 2 X Personal computer Note 1 X XNote 2 X External signal Note 1 X XNote 2 X Class Operation rights Operation Operation Servo ON X Servo OFF Program stop cycle stop X Slot initialization program reset Error reset X Override change Note this is always possible from the T B Override read X Program No change Program No l...

Страница 24: ...tion Support The position restoration support function calculates the correction values of OP data tools and the robot base by only correcting a maximum of several 10 points if a deviation in the joint axis motor replacement hand deformation or a deviation in the robot base occurs and corrects position deviation This function is implemented by optional Personal Computer Support software Use option...

Страница 25: ...tion This function calculates the positions of workpieces arranged in the grid and glass circuit boards in the cassette It helps to reduce the required teaching amount The positions can be given in row by column format single row format or arc format Page 98 4 1 2 Pallet operation Page 189 Def Plt Define pal let Page 236 Plt Pallet User defined area func tion With this function it is possible to s...

Страница 26: ... 1 Mov P1 2 Mov P2 3 Mov P3 4 Mov P4 TEACH 123 DELETE EDIT INSERT POS JNT 100 P1 X 128 56 A 180 00 Y 0 00 B 90 00 Z 845 23 C 180 00 L1 L2 FL1 7 FL2 0 Next 123 TEACH MOVE Prev PROGRAM COPY SRC NAME 1 DSR NAME CLOSE 123 PROGRAM RENAME SRC NAME 1 DST NAME CLOSE 123 MELFA CRnD 7xx Ver P2T RV 6SDL COPYRIGHT C 2008 MITSUBISHI ELEC TRIC CORPORATION ALL RIGHTS RESE RVED PROGRAM DELETE NAME 1 CLOSE 123 PRO...

Страница 27: ...KE 1 ORIGIN 2 BRAKE CLOSE 123 ORIGIN 1 DATA 2 MECH 3 TOOL 4 ABS 5 USER CLOSE 123 ORIGIN DATA D Z1K85K J1 01ag 4 J2 F 15K0 J3 01E27C J4 A 5g 4 J5 05H 30 J6 81 DA9 J7 J8 CLOSE 123 ORIGIN MECH COMPLETED J1 0 J2 0 J3 0 J4 0 J5 0 J6 0 J7 0 J8 0 CLOSE 123 ORIGIN TOOL COMPLETED J1 0 J2 0 J3 0 J4 0 J5 0 J6 0 J7 0 J8 0 CLOSE 123 Ａ 2 Run menu screen 3 Parameter screen 4 Origin Brake screen Check screen Test...

Страница 28: ...3 BATTERY CLOSE 123 HOURE DATA POWER ON TIME 18 Hr BATTERY ACC 14089 Hr CLOSE 123 CLOCK DATE 08 05 07 TIME 16 04 50 CLOSE 123 VERSION R C Ver P2T T B Ver 1 2 1 CLOSE 123 1 Initialize screen 2 Operating time screen 3 Clock screen 4 Version screen CURRENT JOINT 50 M1 TO J1 0 00 J5 0 00 J2 0 01 J6 0 00 J3 0 03 J4 0 00 JOG TOOL XYZ 3軸直交 Jog screen JOG key HAND C HAND1 Z HAND4 B HAND2 Y HAND5 A HAND3 X...

Страница 29: ...d Press the CHARACTER key and in the condition that ABC is displayed on the screen lower side press the character key Whenever the key as which two or more characters are displayed presses the key it changes the input character Ex The ABC key A B C a b c It repeats If it continues and inputs the character currently displayed on the same key once press the key and advance the cursor Ex If it inputs...

Страница 30: ...the arrow keys and move the cursor to 1 Management edit and then press the EXE key The Management edit screen will appear The same operations can be used on the other menu screens NEW PROGRAM PROGRAM NAME CLOSE ABC Correction of the input character CLEAR MNO WXYZ WXYZ WXYZ NEW PROGRAM PROGRAM NAME ABY CLOSE ABC Display the MENU screen from the title screen MODE MANUAL AUTOMATIC Down ENABLE Lightin...

Страница 31: ...age of the screen in the white character These are assigned to F1 F2 F3 and F4 key sequentially from the left The menu currently displayed by pressing the corresponding function key can be selected And if is displayed at the right end of the menu it is shown that there is still the menu other than the current display and whenever it presses the FUNCTION key the display menu changes 3 XYZ CURRENT J...

Страница 32: ...is necessary to specify the tool length in advance using the MEXTL parameter The Tool coordinate system in which the hand tip position is defined depends on the type of robot In the case of a vertical multi joint type robot the direction from the mechanical inter face plane to the hand tip is Z In the case of a horizontal multi joint type robot the upward direction from the mechanical interface pl...

Страница 33: ...eed is displayed on the screen To change these values press either the OVRD OVRD key The following types of jog feed speed are available OVRD key OVRD key LOW and HIGH are fixed dimension feed In fixed dimension feed the robot moves a fixed amount every time the key is pressed The amount of movement depends on the individual robot Table 3 2 Fixed dimension of RV 6SD 3 2 3 JOINT jog Adjusts the coo...

Страница 34: ...Y and Z axis coordinates are adjusted in mm units The A B and C axis coordinates are adjusted in angle units 3 2 5 XYZ jog Adjusts the axis coordinates along the direction of the robot coordinate system The X Y and Z axis coordinates are adjusted in mm units The A B and C axis coordinates are adjusted in angle units Z Y X ＡＣＢＣＢＡＺＹＸＡＡＢＢＣＣ ...

Страница 35: ...sted in mm units The J4 J5 and J6 axis coordinates are adjusted in angle units 3 2 7 CYLNDER jog Adjusting the X axis coordinate moves the hand in the radial direction away from the robot s origin Adjust ing the Y axis coordinate rotates the arm around the J1 axis Adjusting the Z axis coordinate moves the hand in the Z direction of the robot coordinate system Adjusting coordinates of the A B and C...

Страница 36: ... during teaching does not match the tool number during operation To move the robot while switching tool data during the step operation of the program exercise caution as the robot moves to an unexpected direction if the tool data at the time of teaching does not match the tool number during step operation MODE MANUAL AUTOMATIC Down ENABLE Lighting Up DISABLE Rear of T B TOOL SELECT TOOL 0 0 00 0 0...

Страница 37: ...peration including position jump and step feed RV SQ SD series 0 0 1 Detection level during jog operation COLLVLJG Integer 8 Set the detection level sensitivity during jog operation including pause status for each joint axis Unit Make the setting value smaller to increase the detection level sensitivity If an impact error occurs even when no impact occurs during jog operation increase a numeric va...

Страница 38: ...eral devices Operation after Impact If the servo is turned ON while the hand and or arm is interfering with peripheral devices the impact detection state occurs again preventing the servo from being turned ON If an error persists even after repeatedly turning ON the servo release the arm by a brake release operation once and then turn ON the servo again Or release the arm by turning ON the servo a...

Страница 39: ...ss Y key Close Press Y key Opening and closing hand 6 Open Press X key Close Press X key It is possible to mount various tools on the robot s hand area In the case of pneumatic control where the solenoid valve at double solenoid is used two bits of the hand signal is controlled by the open close oper ation of the hand For more information about the hand signal please refer to Page 372 5 12 About t...

Страница 40: ...ment procedure is as follows 1 Push the ENABLE switch of T B and enable T B 2 Press down the enabling switch 3 position switch press the SERVO key and carry out servo on 3 Press the HAND key and display the hand screen 4 Pressing the function key currently assigned to alignment is kept with the enabling switch 3 position switch pressed down While keeping pushing the robot does hand alignment movem...

Страница 41: ...t definition instruction Def Plt and the same posture component values include both 180 degrees and 180 degrees the hand will rotate and move in unexpected ways because the pallet operation calculates positions by dividing the distance between 180 degrees and 180 degrees When using position data whose posture component values include 180 degrees for pallet definitions use either or consistently fo...

Страница 42: ...u screen 2 Press the function key corresponding to new Display the program name input screen 3 Input the program name Display the command edit screen Open the existing program if the existing program name is inputted Input details Function Step No and command statement Example 10 Mov P1 Input as one line of the program Only step No Example 10 Deletes designated line from program Only command state...

Страница 43: ...e CHARACTER key set it in the character input mode Press the MNO M MNO o 3 times and TUV v 3 times in order 4 Input P1 Press the SP space PQRS P Press the CHARACTER key set it in the number input mode and press the 1 key For the instruction word and the data which accompanies the command the space is required Step insertion F3 PROGRAM 1 50 TEACH 123 DELETE EDIT INSERT PROGRAM 1 Ins CLOSE 123 PROGR...

Страница 44: ...e cursor to the next line press the key and select Displaying a specific line Press the FUNCTION key and change the function display and press the F2 key The display changes to the JUNP screen The specification line can be displayed if the step number to display in the parenthesis is inputted and the EXE key is pressed The step number can be omitted when inserting It is inserted in the next of the...

Страница 45: ...rogram F4 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54 1851 COPY 123 POSI EDIT NEW Precautions when saving programs Make sure to perform the operation above The edited data will not be updated if the power is turned off without doing so after modifying a program on the program edit screen Moreover as much as possible try...

Страница 46: ...key 3 times Move the cursor to o Press the CLEAR key twice and delete ov Leave M Press the TUV key 3 times input v the key the PQRS key 4 times input s Then 5 step is Mvs P5 Press the EXE key and reg ister step 5 PROGRAM 1 50 1 Mov P1 2 Mov P2 3 Mov P3 4 Mov P4 TEACH 123 DELETE EDIT INSERT PROGRAM 1 50 1 Mov P1 2 Mov P2 3 Mov P3 4 Mov P4 BWD 123 JUMP FWD PROGRAM 1 50 STEP 5 CLOSE 123 Call the step...

Страница 47: ...nded for closing is pressed in the middle of correction Correction of the character Move the cursor to up to the mistaken character and input the correct character after pressing the CLEAR key and deleting leftward If the program is corrected If the program is corrected certainly save Function key F4 which correspond for closing are pushed or push the ENABLE switch on the back of T B and disable T...

Страница 48: ...ion Press the function key corresponding to Teach F4 then the confirmation screen is displayed 3 Press the function key corresponding to Yes then the robot s current position data will be taught to P5 and display will return to the original command edit screen The teaching can be canceled if the function key corresponding to No is pressed The teaching of the current position was completed above Ca...

Страница 49: ...en The teaching can be canceled if the function key corresponding to No is pressed The teaching of the current position was completed above PROGRAM 1 1 Mov P1 2 Mov P2 3 Mov P3 4 Mov P4 CLOSE 123 CHANGE DIRECT Display the current position F2 POS JNT 50 P1 X 0 00 A 0 00 Y 0 00 B 0 00 Z 0 00 C 0 00 L1 0 00 L2 0 00 FL1 0 FL2 0 Prev 123 TEACH MOVE Next POS JNT 50 P1 X 0 00 A 0 00 Y 0 00 B 0 00 Z 0 00 ...

Страница 50: ...ed one by one by Prev F3 and Next F4 Usually although it is the call of only the position variable change the function key and the call can do the joint variable by the name F2 After calling the joint variable the joint variable of order can be called one by one by Prev F3 and If it displays to the head or the last by the joint variable it will return to the position variable by the next display P...

Страница 51: ...UNCTION key is pressed 4 Deletion of the position variable Press the function key corresponding to Yes then the position variable is deleted Display the position edit screen F2 PROGRAM 1 1 Mov P1 2 Mov P2 3 Mov P3 4 Mov P4 CLOSE 123 CHANGE DIRECT POS JNT 50 P1 X 0 00 A 0 00 Y 0 00 B 0 00 Z 0 00 C 0 00 L1 0 00 L2 0 00 FL1 0 FL2 0 Prev 123 TEACH MOVE Next Call the position 55 F3 F4 POS JNT 50 P55 X ...

Страница 52: ...ached or it presses down still more strongly servo off will be carried out and the robot will stop The robot moves by this operation When the robot moves confirm not interfering with peripheral equipment etc beforehand We recommend you to lower speed at first And also important to predicting the trajectory of the robot by moving mode the joint the XYZ of operation Name Movement method Joint mode T...

Страница 53: ...Display the position edit screen Press the function key corresponding to Cange and display the position edit screen 2 Input 50 00 into Z axis element Press the key twice and move the cursor to the Z axis Press the CLEAR key and delete 0 00 currently displayed Press 5 0 and the EXE key As for the position variable P50 only the value of the Z axis is registered as the 50mm Display the position edit ...

Страница 54: ...the screen If F1 FWD is released during this step the robot will stop And detach the enabling switch 3 posi tion switch or push in still more strongly thing servo off can be carried out and execution can be stopped During execution the lamp on the controller s START switch will light If execution of the one step is completed LED of the START switch will go out and LED of the STOP switch will turn ...

Страница 55: ...the front step Supplement If it does step return after carrying out the step feed of the following program to Step 4 and step return is further done after returning to P1 it will return to the position at the time of the start which did step feed The position at the time of the start is the position which began to execute Step 1 Take special care to the robot movements during automatic operation I...

Страница 56: ...e EXE key Immediately stopping the robot during operation Press the EMG STOP emergency stop switch The servo will turn OFF and the moving robot will immediately stop To resume operation reset the alarm turn the servo ON and start step operation Release or for cibly press the enable switch The servo will turn OFF and the moving robot will immediately stop To resume operation lightly press the enabl...

Страница 57: ...is detached the cursor of the T B screen will move to the following step Take special care to the robot movements during automatic operation If any abnormality occurs press the EMG STOP switch and immediately stop the robot 4 Step jump It is possible to change the currently displayed step or line The operation in the case of doing step operation from Step 5 as an example is shown 1 Call Step 5 Pre...

Страница 58: ...ion key corresponding to FWD is pressed step feed can be done from Step 5 Take special care to the robot movements during automatic operation If any abnormality occurs press the EMG STOP switch and immediately stop the robot PROGRAM 1 50 4 Mov P4 5 Mov P5 6 Mov P6 7 End BWD 123 Jump FWD PROGRAM 1 50 4 Mov P4 5 Mov P5 6 Mov P6 7 End BWD 123 Jump FWD CAUTION ...

Страница 59: ... HIGH 3 5 10 30 50 70 100 The speed will decrease in reverse each time the OVRD keys are pressed 2 Selecting the program No 1 Set the T B ENABLE switch to DIS ABLE 2 Set the controller MODE switch to AUTOMATIC 3 Press the CHNG DISP switch and dis play PROGRAM NO on the STATUS NUMBER display When the UP switch is pressed the registered program Nos will scroll up and then the DOWN switch is pressed ...

Страница 60: ... B ENABLE switch to DISABLE 2 Set the controller MODE switch to AUTO MATIC 3 Push the SVO ON switch of the controller and servo power turn on 4 Automatic operation will start when the controller START switch is pressed Continuous operation If the END switch is pressed during the continuous operation the program will stop after one cycle The LED blinks during the cycle stop Before starting automati...

Страница 61: ...tors cannot enter unintentionally Make sure that there are no unnecessary items such as tools inside the robot operation range Make sure that the workpiece is correctly placed at the designated position Confirm that the program operates correctly with step operation 1 Set the T B ENABLE switch to DISABLE 2 Set the controller MODE switch to AUTOMATIC 3 Automatic operation will start when the contro...

Страница 62: ...ENABLE 3 Press the EXE key while holding down the RESET key The execution line will return to the head and the program will be reset RESET CHNG DISP Reset T B disable Controller enable Execute of program reset DisplaytheprogramNo MODE MANUAL AUTOMATIC Down ENABLE Lighting Up DISABLE Rear of T B Program reset RESET EXE Execute of program reset T B enable Controller disable Down ENABLE Lighting Up D...

Страница 63: ...perating with the controller 1 Set the T B ENABLE switch to DISABLE 2 Set the controller MODE switch to AUTO MATIC 3 When the SVO ON switch is pressed the servo will turn ON and the SVO ON lamp will light 4 When the SVO OFF switch is pressed the servo will turn OFF and the SVO OFF lamp will light Execute servo ON T B enable Controller disable Prepare the T B Servo ON operation SERVO Down ENABLE Li...

Страница 64: ...used to cancel such errors temporarily For instance if the axes are outside the movement range perform a jog operation to adjust the axes while the error is canceled temporarily Operation to cancel errors temporarily from the T B 1 Set the Mode selection switch on the front of the controller to MANUAL 2 Set the T B ENABLE switch to ENABLE 3 Hold the enabling switch lightly hold down the SERVO key ...

Страница 65: ... menu Press the 1 key in the menu screen 1 Management and edit are selected and display the list of the programs Same operation can be done even if the cursor is moved to 1 management and edit by the or key and it presses the EXE key And the program which is the target of each operation can also be selected The menu Edit Position New Copy corresponding to the function key is displayed under the sc...

Страница 66: ...put the program name copied in the parenthesis of the copy destination and press the EXE key PROGRAM COPY SRC NAME 1 DSR NAME CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54 1851 COPY 123 POSI EDIT NEW PROGRAM COPY SRC NAME 1 DSR NAME 21 CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 5...

Страница 67: ...e 1 If it changes move the cursor by the arrow key Into the parenthesis of the renaming destination input the new program name and press the EXE key PROGRAM RENAME SRC NAME 1 DST NAME CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54 1851 COPY 123 POSI EDIT NEW FILE EDIT 1 20 Rem 136320 2 08 04 24 14 56 08 694 3 08 ...

Страница 68: ...l return to the program list display If it does not delete press the function key corresponding to No It returns to the deletion screen PROGRAM DELETE NAME 1 CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54 1851 RENAME DELETE PRTCT CLOSE 123 PROGRAM DELETE 31 DELETE OK No 123 Yes PROGRAM DELETE NAME 31 CLOSE 123 FI...

Страница 69: ...ding to Data If the function key corresponding to ON is pressed it will be set up for protecting If the function key corresponding to OFF is pressed it will be set up for not protecting PROTECT NAME 1 protect COMMAND OFF DATE OFF CLOSE 123 DATA CMD FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54 1851 RENAME DELETE PRTCT CLO...

Страница 70: ...eration In initialization operation protection information is disregarded and execute initialization About data protection It is the function which protects the variable from the substitution to each variable by registration of the position data based on the operation mistake change and the mistaken execution of the program Protection information is not copied in copy operation In initialization o...

Страница 71: ...t and the robot will start moving If F1 FWD is released during this step the robot will stop And detach the enabling switch 3 position switch or push in still more strongly thing servo off can be carried out and execution can be stopped During execution the lamp on the controller s START switch will light 1 If execution of the one step is completed LED of the START switch will go out and LED of th...

Страница 72: ...e to the robot movements during automatic operation If any abnormality occurs press the EMG STOP switch and immediately stop the robot About step operation Step operation executes the program line by line The operation speed is slow and the robot stops after each line so the program and operation position can be confirmed During execution the lamp on the controller s START switch will light Execut...

Страница 73: ...immediately stop To resume operation reset the alarm turn the servo ON and start step operation Release or for cibly press the enable switch The servo will turn OFF and the moving robot will immediately stop To resume operation lightly press the enable switch and start step operation Release the F1 FWD key The step execution will be stopped The servo will not turn OFF To resume operation press the...

Страница 74: ...switch and immediately stop the robot 4 Step feed in another slot When checking a multitask program it is possible to perform step feed in the confirmation screen of the operation menu not in the edit screen Refer to Page 43 3 Step feed in another slot for operation method 5 Finishing of the confirmation screen 1 Press the function key corresponding to Close and return to the operation menu screen...

Страница 75: ...eration menu screen MENU 1 FILE EDIT 2 RUN 3 PARAM 4 ORIGIN BRK 5 SET INIT CLOSE 123 RUN 1 CHECK 2 TEST RUN CLOSE 123 TEST RUN 1 Mov P1 PROG NAME 1 STEP 1 MODE CONT CLOSE 123 CSTOP RUN 1 CHECK 2 TEST RUN CLOSE 123 TEST RUN 1 Mov P1 PROG NAME 1 STEP 1 MODE CYCLE CLOSE 123 CSTOP TEST RUN 1 Mov P1 PROG NAME 1 STEP 1 MODE CONT CLOSE 123 CSTOP RUN 1 CHECK 2 TEST RUN CLOSE 123 TEST RUN 1 Mov P1 PROG NAM...

Страница 76: ...r 1 Press the 1 key in the monitor menu screen and display the input signal screen The input signal of the 32 points can be monitored on the one screen The case where the state of the input signals 8 15 is confirmed is shown in the following 2 Press the function key corresponding to Number Set 8 as the start number MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 ...

Страница 77: ... 40 71 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 56 1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 NUMBER CLOSE 123 Next Prev INPUT 3 2 1 0 9 8 7 6 5 4 3 2 1 0 9 8 23 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 8 39 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 24 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 NUMBER CLOSE 123 Next Prev INPUT 3 2 1 0 9 8 7 6 5 4 3 2 1 0 9 8 23 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 8 39 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 24 9 8 7 6 5 4 3 ...

Страница 78: ... indicates ON and white indicates OFF Press the function key corresponding to Next then display the next output signal screen Press the function key corresponding to Prev then display the previous output screen OUTPUT 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 15 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 0 31 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 16 1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 NUMBER CLOSE 123 Next Prev MONITOR 1 INPUT ...

Страница 79: ...sponding to Close and return to the monitor menu screen OUTPUT START No 8_ 5432109876543210 OUT VALUE 0000000000000000 CLOSE 123 OUTPUT OUTPUT 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 15 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 0 31 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 16 1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 NUMBER CLOSE 123 Next Prev OUTPUT 1 Mov P1 START No 8_ 3210987654321098 OUT VALUE 0000000000000001 CLOSE 123 OUTPUT OU...

Страница 80: ... at the head for the input register No 8000 Press the function key corresponding to Next then display the next input register screen Press the function key corresponding to Prev then display the previous input register screen MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 ...

Страница 81: ...red on the one screen The case where the state of the output register 8000 is confirmed is shown in the following INPUT REGISTER 8000 0 0 0000 8001 0 0 0000 8002 0 0 0000 8003 0 0 0000 CLOSE 123 NUMBER Prev Next MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 FILE EDIT 1 20 Rem 136...

Страница 82: ... to the output value by the arrow key and input 10 The unnecessary character should press and erase the CLEAR key If it sets up by the hexadecimal number move the cursor to 0x by the arrow key and input C The unnecessary character should press and erase the CLEAR key Press the function key F1 corresponding to the Output then will actually output the set up value 5 Press the function key correspond...

Страница 83: ... menu screen OUTPUT REGISTER 6000 0 0 0000 6001 0 0 0000 6002 0 0 0000 6003 0 0 0000 CLOSE 123 NUMBER Prev Next MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24 14 56 08 694 A1 08 04 24 13 05 54 2208 B1 08 04 24 13 05 54...

Страница 84: ...e Name and input the variable name to monitor 4 Display the value of the numeric variable M1 on the screen The variable which will be monitored if the cursor is moved to the line which is vacant in the arrow key and operation of the above 3 is repeated can be added The variable which can be monitored simultaneously is to the three pieces MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE...

Страница 85: ...ABLE NAME DATA M1 1 CLOSE 123 VARIABLE SLOT 1 5 M1 8 P1 595 40 0 00 829 C1 CLOSE 123 VALUE SLOT NAME VARIABLE SLOT 1 5 M1 8 P1 595 40 0 00 829 C1 CLOSE 123 VALUE SLOT NAME MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 FILE EDIT 1 20 Rem 136320 1 08 04 24 17 20 32 22490 2 08 04 24...

Страница 86: ...arrow key MONITOR 1 INPUT 2 OUTPUT 3 INPUT REG 4 OUTPUT REG 5 VARIABLE 6 ERROR LOG CLOSE 123 ERROR LOG No 0001 H0120 08 05 08 16 51 00 Instantaneous power failure CLOSE 123 ERROR LOG No 0002 L1826 08 05 08 16 49 22 Pos data disagree Check origin CLOSE 123 ERROR LOG No 0001 H0120 08 05 08 16 51 00 Instantaneous power failure CLOSE 123 The right of operation is unnecessary It operates even when T B ...

Страница 87: ...cessary number by the CLEAR key If the EXE key is pressed the buzzer will sound the value will be fixed and it will return to the screen of the parameter If the function key corresponding to the Close is pressed also after inputting the new preset value change can be canceled and it can return to the parameter screen And press the function key corresponding to Next will display the next parameter ...

Страница 88: ...v PARAMETER NAME MEXTL1 ELE DATA 0 00 0 00 0 00 0 00 0 00 0 00 CLOSE 123 Next DATA Prev PARAMETER NAME MEXTL ELE DATA 0 00 0 00 100 00 0 00 0 00 0 00 CLOSE 123 Next DATA Prev F3 F2 PARAMETER NAME MEXTL ELE 3 DATA 0 00 0 00 0 00 0 00 0 00 0 00 CLOSE 123 Next DATA Prev PARAMETER MEXTL 0 00 0 00 100 00 0 00 0 00 0 00 CLOSE 123 Next DATA Prev Power must be turned ON again The changed parameter will be...

Страница 89: ...ays assign an operator other than the T B operator to prevent the arm from dropping This operation must be carried out with the T B operator giving signals Refer to Table 3 6 and accurately designate the axis for which the brakes are to be released Table 3 6 The brake release axis unit classified by type Note mark means that brake release with the independent axis is possible The operation method ...

Страница 90: ...t with the T B operator giving signals Refer to Table 3 6 and accurately designate the axis for which the brakes are to be released 4 Press function key continuously coresponding to Relese to release the brake of the specified axis only while the keys are pressed The brakes will activate when the function key or enabling switch is released BRAKE J1 0 J2 0 J3 1 J4 0 J5 0 J6 0 J7 0 J8 0 CLOSE 123 RE...

Страница 91: ...tial screen 1 Initialize the program Delete all the programs 1 Press the 1 key in the set initial screen and display the initial menu screen 2 Press the 1 key in the initial menu screen and select the program Display the screen of confirmation 3 If it initializes press the function key corresponding to Yes If it does not initialize press the function key corresponding to no The screen returns to i...

Страница 92: ...corresponding to Yes If it does not initialize press the function key corresponding to no The screen returns to initiali menu screen INITIALIZE 1 DATA 2 PARAMETER 3 BATTERY CLOSE 123 SET INITIALIZE 1 INITIALIZE 2 POWER 3 CLOCK 4 VERSION CLOSE 123 Executed even when protected The program will be initialized even if the program protection or variable protection is set to ON SET INITIALIZE 1 INITIALI...

Страница 93: ...e press the function key corresponding to no The screen returns to initiali menu screen 4 Press the function key corresponding to Close and return to the set initial screen INITIALIZE 1 DATA 2 PARAMETER 3 BATTERY CLOSE 123 SET INITIALIZE 1 INITIALIZE 2 POWER 3 CLOCK 4 VERSION CLOSE 123 SET INITIALIZE 1 INITIALIZE 2 POWER 3 CLOCK 4 VERSION CLOSE 123 INITIALIZE 1 DATA 2 PARAMETER 3 BATTERY CLOSE 123...

Страница 94: ...lated in the controller and a caution message is displayed when the battery is spent Always initialize the battery consumption time after replacing the battery to ensure that the caution message is displayed correctly If this initialization is carried out when the battery has not been replaced the display timing of the caution message will deviate Thus carry this step out only when the battery has...

Страница 95: ... in the set initial screen and display the version screen 2 Press the function key corresponding to Close and return to the set initial screen CLOCK DATE 08 05 07 TIME 16 35 20 CLOSE 123 SET INITIALIZE 1 INITIALIZE 2 POWER 3 CLOCK 4 VERSION CLOSE 123 SET INITIALIZE 1 INITIALIZE 2 POWER 3 CLOCK 4 VERSION CLOSE 123 VERSION R C Ver P2T T B Ver 1 2 1 CLOSE 123 VERSION R C Ver P2T T B Ver 1 2 1 CLOSE 1...

Страница 96: ...of F1 key and F3 key of T B 1 Set the display language The character displayed on the T B can be set to either Japanese or English 1 Press the F1 key in the initial setting screen and select 1 Configuration 2 Press the F1 key and select 1 Default Language 3 Display the JPN by F1 or F2 key then language is set as Japanese And display the ENG then language is set as English EXE 1 F1 2 F2 キ 1 Configu...

Страница 97: ...pressed 7 T B starts in the language set up when the EXE key was pressed Japanese English Default Language 002 JPN UP DWN Back Default Language 001 ENG UP DWN Back 1 Default Language 2 Contrast 1 2 Next 1 Save and Exit 2 Exit without Save 1 2 Prev 1 Default Language 2 Contrast 1 2 Next 1 Save and Exit 2 Exit without Save 1 2 Prev 1 Configuration 2 Com Information 1 2 Rset 1 Configuration 2 Com Inf...

Страница 98: ... bright the F1 key is pressed if it makes it dark press the F2 key and set it as the good brightness It becomes so bright that the numerical value is large 5 Press the EXE key and fix it 6 Press the EXE key and display finish screen 1 Configuration 2 Com Information 1 2 Rset 1 Default Language 2 Contrast 1 2 Next Contrast 012 UP DWN Back 1 Default Language 2 Contrast 1 2 Next 1 Default Language 2 ...

Страница 99: ...tting screen And the setup can be done over again if the EXE key is pressed 8 T B starts in the contrast set up when the EXE key was pressed 1 Save and Exit 2 Exit without Save 1 2 Prev 1 Configuration 2 Com Information 1 2 Rset 1 Configuration 2 Com Information 1 2 Rset MELFA RV 12SQ SZ Ver 1 0 CRnQ 7xx COPYRIGHT C 2007 MITSUBISHI ELEC TRIC CORPORATION ALL RIGHTS RESE RVED ...

Страница 100: ...Mvc 4 4 Continuous movement Cnt 5 5 Acceleration deceleration time and speed control Accel Oadl 6 6 Confirming that the target position is reached Fine Mov and Dly 7 7 High path accuracy control Prec 8 8 Hand and tool control HOpen HClose Tool 9 4 1 2Pallet operation Def Plt Plt 10 4 1 3Program control 1 Unconditional branching conditional branching waiting GoTo If Then Else Wait etc 11 2 Repetiti...

Страница 101: ... P2 50 1 2 Moves from P2 to a position retracted 50mm in the hand direction 3 Mov P2 3 Moves to P2 4 Mov P3 100 Wth M_Out 17 1 4 Starts movement from P3 to a position retracted 100mm in the hand direction and turns ON output signal bit 17 5 Mov P3 5 Moves to P3 6 Mov P3 100 1 6 Returns from P3 to a position retracted 100mm in the hand direction 7 End Ends the program Function Explanation page Desi...

Страница 102: ...ion 3 Mvs 50 1 3 Moves with linear interpolation from the current position P1 to a position retracted 50mm in the hand direction 4 Mvs P2 100 Wth M_Out 17 1 1 4 Output signal bit 17 is turned on at the same time as the robot starts moving 5 Mvs P2 5 Moves with linear interpolation to P2 6 Mvs 100 1 6 Moves with linear interpolation from the current position P2 to a position retracted 50mm in the h...

Страница 103: ...le from the start point to the end point is 0 deg fan angle 180 deg It is possible to specify the interpolation form using the TYPE instruction An appended statement Wth or WthIf can be designated Mvc Designates the start point end point transit point 1 and transit point 2 and moves the robot with circular interpolation in order of the start point transit point 1 transit point 2 end point An appen...

Страница 104: ... the circumference on which the center point P8 start point P7 and end point P9 are designated 5 Mvc P9 P10 P11 5 Moves between P9 P10 P11 P9 as an arc The robot current position before movement is separated from the start point so first the robot will move with linear operation to the start point 1 cycle operation 6 End Ends the program Function Explanation page Designate the movement speed Page ...

Страница 105: ...ovement 8 Cnt 0 Invalidates the continuous movement 9 End Ends the program Function Explanation page Designate the movement speed Page 93 5 Acceleration deceleration time and speed control Designate the acceleration deceleration time Page 93 5 Acceleration deceleration time and speed control Confirm that the target position is reached Page 95 6 Confirming that the target position is reached Move w...

Страница 106: ...ether the optimum acceleration deceleration function should be enabled or disabled Statement example Explanation Accel Sets both the acceleration and deceleration to 100 Accel 60 80 Sets the acceleration to 60 and the deceleration to 80 For maximum acceleration deceleration is 0 2 sec acceleration 0 2 0 6 0 33 sec deceleration 0 2 0 8 0 25 sec Ovrd 50 Sets the joint interpolation linear interpolat...

Страница 107: ...l 70 70 Sets the acceleration and deceleration to 70 of the maximum speed 9 Mvs P3 4 Moves linearly to P3 with the end speed 120mm s 10 Spd M_NSpd Returns the end speed to the default value 11 JOvrd 70 Sets the speed for joint interpolation to 70 12 Accel Returns both the acceleration and deceleration to the maximum speed 13 Mvs 50 1 5 Moves linearly with the default speed for linear movement from...

Страница 108: ...complete pulse count is 50 or less 6 M_Out 17 1 4 Turns output signal 17 ON when positioning finish pulse reaches 50 pulses 7 Fine 1000 Sets positioning finish pulse to 1000 8 Mvs P3 100 1 5 Moves linearly from P3 to position retracted 100mm in hand direction 9 Mvs P3 6 Moves with linear interpolation to P3 10 Dly 0 1 Performs the positioning by the timer 11 M_Out 17 0 7 Turns output signal 17 off...

Страница 109: ...erpolation from P1 to position retracted 50mm in hand direction 2 Ovrd 50 Sets the movement speed to half of the maximum speed 3 Mvs P1 2 Moves with linear interpolation to P1 4 Prec On The high path accuracy mode is enabled 5 Mvs P2 3 Moves the robot from P1 to P2 with high path accuracy 6 Mvs P3 4 Moves the robot from P2 to P3 with high path accuracy 7 Mvs P4 5 Moves the robot from P3 to P4 with...

Страница 110: ...Mvs 50 1 4 Moves linearly from current position P1 to position retracted 50mm in hand direction Lifts up workpiece 10 Mvs P2 50 1 5 Moves with joint interpolation from P2 to position retracted 50mm in hand direction 11 Ovrd 50 Sets movement speed to half of the maximum speed 12 Mvs P2 6 Moves with linear interpolation to P2 Goes to place workpiece 13 Dly 0 5 Wait for the 0 5 seconds for the comple...

Страница 111: ...o operate pallet No 1 with a start point P1 end point A P2 end point B P3 and diagonal point P4 a total of 12 work positions quantity A 4 quantity B 3 and a pallet pattern 1 Zigzag Def Plt 2 P1 P2 P3 8 5 2 Defines to operate pallet No 2 with a start point P1 end point A P2 and end point B P3 a total of 40 work positions quantity A 8 quantity B 5 and a pallet pattern 2 Same direction Def Plt 3 P1 P...

Страница 112: ... change the sign of 179 degrees to add 360 degrees and correct the value to 181 degrees Program example 1 shows an example where the posture components of the end points P3 and P4 and diagonal point P5 are adjusted according to the start point P2 when the hand direction is the same in all grid points of a pallet values of the A B and C axes are identical line numbers 10 to 90 Program exam ple 2 sh...

Страница 113: ...nd B and the diagonal point of the pallet definition The value of the start position of the pallet definition is employed for the multi rotation flag of grid points FL2 of position data as well If position data with different multi rotation flags are used for each point of the pallet definition the hand will rotate and move in unexpected ways depending on the robot positions the pallet operation g...

Страница 114: ...ble M1 M1 is used as a counter 12 LOOP Designates label LOOP at the jump destination 13 Mov P1 50 1 Moves with joint interpolation from P1 to a position retracted 50mm in hand direction 14 Ovrd 50 Sets movement speed to half of the maximum speed 15 Mvs P1 Moves linearly to P1 Goes to grasp workpiece 16 HClose 1 Closes hand 1 Grasps workpiece 17 Dly 0 5 Waits 0 5 seconds 18 Ovrd 100 Sets movement s...

Страница 115: ... P3 P4 P5 3 5 2 Defines the pallet Pallet No 1 start point P2 end point A P3 end point B P4 diagonal point P5 quantity A 3 quantity B 5 pallet pattern 2 Same direction 12 M1 1 Substitutes value 1 in numeric variable M1 M1 is used as a counter 13 LOOP Designates label LOOP at the jump destination 14 Mov P1 50 1 Moves with joint interpolation from P1 to a position retracted 50mm in hand direction 15...

Страница 116: ... V functions 4MELFA BASIC V Related functions Function Explanation page Substitute operation Page 113 4 1 6 Expressions and operations Condition branching Page 104 1 Unconditional branching conditional branching waiting ...

Страница 117: ... and the designated conditions of that value The value conditions can be designated randomly Multiple types of conditions can be designated per command statement Wait Waits for the variable to reach the designated value Statement example Explanation GoTo 200 Jumps unconditionally to step 200 GoTo FN Jumps unconditionally to the label FIN step ON M1 GoTo L1 L2 L3 If the numeric variable M1 value is...

Страница 118: ...IC V functions 4MELFA BASIC V Related functions Function Explanation page Repetition Page 106 2 Repetition Interrupt Page 107 3 Interrupt Subroutine Page 108 4 Subroutine External signal input Page 111 1 Input signals ...

Страница 119: ... Next Repeat between For statement and Next statement 10 times The initial numeric variable M1 value is 1 and is incremented by one with each repetition For M1 0 To 10 Step 2 Next Repeat between For statement and Next statement 6 times The initial numeric variable M1 value is 0 and is incremented by two with each repetition While M1 1 And M1 10 WEnd Repeat between While statement and WEnd statemen...

Страница 120: ...eration time depends on the Accel and Ovrd instructions Def Act 2 M_In 11 1 GoSub SUB2 L If input signal bit 11 is turned on for interrupt number 2 the subroutine on step SUB2 is defined to be called after the statement currently being executed is completed Def Act 3 M_In 12 1 GoSub SUB3 S If input signal bit 12 is turned on for interrupt number 3 the subroutine on step SUB3 is defined to be calle...

Страница 121: ...d program as an argument FPrm An argument is transferred with the program called with the CallP command Statement example Explanation GoSub Calls the subroutine from step On GoSub Calls the subroutine from label GET ON M1 GoSub L1 L2 L3 If the numeric variable M1 value is 1 calls the subroutine at step L1 if 2 calls the subroutine at step L2 and if 3 calls the subroutine at step L3 If the value do...

Страница 122: ...s at a designated time width Command word Statement example Related functions Command word Explanation Dly Functions as a designated time timer Statement example Explanation Dly 0 05 Waits for only 0 05 seconds M_Out 10 1 Dly 0 5 Turns on output signal bit 10 for only 0 5 seconds Function Explanation page Pulse signal output Page 111 1 Input signals ...

Страница 123: ... program In continuous operation the program is executed again from the start step upon the execution of the End instruction In cycle operation the program ends upon the execution of the End instruction when the cycle is stopped Statement example Explanation Hlt Interrupt execution of the program If M_In 20 1 Then Hlt Pauses the program if input signal bit 20 is turned on Mov P1 WthIf M_In 18 1 Hl...

Страница 124: ... reach the designated state Statement example Explanation Wait M_In 1 1 Waits for the input signal bit 1 to turn ON M1 M_Inb 20 Substitutes the input signal bit 20 to 27 as an 8 bit state in numeric variable M1 M1 M_Inw 5 Substitutes the input signal bit 5 to 20 as an 16 bit state in numeric variable M1 Function Explanation page Signal output Page 111 2 Output signals Branching with input signal P...

Страница 125: ... When X 123 7 Y 238 9 Z 33 1 A 19 3 B 0 C 0 FL1 1 FL2 0 Print 1 M5 P5 Outputs the numeric variable M5 value and position variable coordinate value to file No 1 M5 and P5 are separated with a comma hexadecimal 2C Output data example 8 123 7 238 9 33 1 19 3 0 0 1 0 CR When M5 8 P5 X 123 7 Y 238 9 Z 33 1 A 19 3 B 0 C 0 FL1 1 FL2 0 Input 1 M3 Converts the input data into a value and substitutes it in ...

Страница 126: ...ide the numeric variable M1 value by 2 Exponential operation M1 M1 2 Square the numeric variable M1 value Integer division M1 M1 3 Divide the numeric variable M1 value by 3 and make an integer round down MOD Remainder operation M1 M1 Mod 3 Divide the numeric variable M1 value by 3 and leave redundant Sign reversal P1 P1 M1 M1 Reverse the sign for each coordinate element in position variable P1 Rev...

Страница 127: ...put the numeric variable M1 value to output signal bit 20 to 27 Output bit signal 27 is always ON at this time Not NOT operation M1 Not M_Inw 1 Reverse the status of input signal bit 1 to 16 to create a value and substitute in numeric variable M1 Xor Exclusive OR operation N2 M1 Xor M_Inw 1 Obtain the exclusive OR of the states of M1 and the input signal bits 1 to 16 convert into a value and subst...

Страница 128: ... A relative to the posture of P1 Multiplication corresponds to addition within the tool coordinate system while division corresponds to subtraction within the tool coordinate sys tem 3 Relative calculation of position data Addition An example of relative calculation Addition 1 P2 5 10 0 0 0 0 0 0 2 P100 P1 P2 3 Mov P1 4 Mvs P100 P1 200 150 100 0 0 45 4 0 In this example the hand is moved relativel...

Страница 129: ...ns output signal bit 20 ON simultaneously with the start of movement to P1 Mov P1 WITHIF M_In 20 1 Hlt Stops if the input signal bit 20 turns ON during movement to P1 Mov P1 WthIf M_In 19 1 Skip Stops movement to P1 if the input signal bit 19 turns ON during movement to P1 and then proceeds to the next step Function Explanation page Joint interpolation movement Page 88 1 Joint interpolation moveme...

Страница 130: ...y activating it from the operation panel or by a dedicated input signal or by executing an instruction related to multitask operation The execution environment for multitasking is shown in Fig 4 1 Fig 4 1 Multitask slot environment User base program Multitask slot environment External variables user defined external variables Slot 1 XRUN XLOAD XRST XSTP Program Slot 2 Slot n Program Program XCLR E...

Страница 131: ...pe depending on the setting of the information of the SLT parameter the start operation starts concurrent execution or con stant concurrent execution or starts concurrent execution at error occur rence It is necessary to set the SLT parameter in advance This method does not rely on the program flow and is effective for carry ing out simultaneous execution with a preset format or for sequential exe...

Страница 132: ...ram eters for details 3 Starting conditions START START Execution of a pro gram using the START but ton on the operation panel or the I O START signal Select START when it is desired to start normally Note1 Note1 The start operation conducted from the operation panel or by sending the dedicated input signal START will start the execution of programs of all the task slots whose start conditions are...

Страница 133: ...ecified in task slot 1 that the signal is turned on by means of the external vari able M_00 4 Confirmation of operating status of programs via robot status variables The status of the program running with multitask can be referred to from any slot using the robot status vari ables M_Run M_Wai M ERR Example M1 M_Run 2 The operation status of slot 2 is obtained Refer to Page 140 4 3 26 Robot status ...

Страница 134: ...ted output signal START turns on If all the pro grams stop the LED of the STOP switch is lit and the dedicated output signal STOP turns on The dedicated output signals S1START to S32START and S1STOP to S32STOP output the operation sta tus for each of the task slots If it is necessary to know the individual operation status signal numbers can be assigned to the dedicated input output parameters and...

Страница 135: ...e position data lead in program Process flow P1 Workpiece pickup position Vacuum timer Dly 0 05 P2 Workpiece placing position Release timer Dly 0 05 P3 Vision pre position Do not stop at penetration point Cnt P4 Vision shutter position Do not stop at penetration point Cnt P_01 Vision compensation data P20 Position obtained by adding P2 to vision compensation data relative operation Workpiece picku...

Страница 136: ...ng position 24 M_Out 10 1 Place workpiece 25 Dly 0 05 Timer 0 05 second 26 Mov P20 10 Move to 10mm above P20 27 Cnt 0 Invalidate path connected movement 28 End End one cycle 2 Position data lead in program Program name 2 1 R 2 If M_01 0 Then GoTo R Wait for interlock variable M_01 to reach 1 3 Open COM1 AS 1 Open RS 232 C line 4 Dly M_03 Hypothetical process timer 0 05 second 5 Print 1 SENS Transm...

Страница 137: ...ea cannot be increased by mounting expansion memory 3 Program execution area The program execution area is used when operating a program automatically The capacity of the program execution area is 184 Kbytes The total capacity of programs loaded into the execution area at the same time via user base programs for multitasking purposes or by XRun and CallP instructions must be 184 Kbytes or less The...

Страница 138: ...4 125 Multitask function 4MELFA BASIC IV Total 220 KB 179KB Program edit area Program save area file system Program execution area Total 184KB Capacity in the case of standard memory ...

Страница 139: ... use an external output signal to select a program to be exe cuted the program name should be specified using the numbers If a program is executed as a sub pro gram via the CallP instruction more than four alphabetic characters may be used However such programs may not be selected from the operation panel 2 Command statement Example of constructing a statement 1 Mov P1 Wth M_Out 17 1 1 2 3 4 1 STE...

Страница 140: ...moves to the position saved in variable name J1 A numeric value integer real value etc is saved The variable name starts with M Example M1 1 The value 1 is substituted in variable name M1 A character string is saved A is added to the end of the variable name Example C1 ERROR the character string ERROR is substituted in variable name C1 Note 1 Each variable is categorized into the following classes...

Страница 141: ...is stored in the memory it is stored in the order of the step Nos Step Nos can be any integer from 1 to 32767 4 3 5 Label A label is a user defined name used as a marker for branching A label can be created by inserting an asterisk followed by uppercase or lowercase alphanumeric char acters after the step No The head of the label must be an alphabetic character and the entire label must be within ...

Страница 142: ...s Class Available characters Program name Variable name Label name Alphabetic characters A B C D E F G H I J K L M N O P Q R S T U V W X Y Z O O O a b c d e f g h i j k l m n o p q r s t u v w x y z X Note1 Note1 Alphanumerics in variable names and label names in the program are automatically converted into uppercase characters Note 1 Numerals 0 1 2 3 4 5 6 7 8 9 O Note2 Note2 Only alphabetical ch...

Страница 143: ...statement Example 1 Mov P1 GET GET will be set as the comment 2 GET PARTS This is the same as 150 Rem GET PARTS 4 Asterisk The asterisk is placed in front of label names used as the branch destination Example 2 CHECK 5 Comma The comma is used as a delimiter when there are several parameters or suffixes Example P1 200 150 6 Period The period is used for obtaining certain components out of multiple ...

Страница 144: ... following characteris tics 1 Decimal number Example 1 1 7 10 5 1 2E 5 Exponential notation Valid range 1 7976931348623157e 308 to 1 7976931348623157e 308 2 Hexadecimal number Example H0001 HFFFF Valid range H0000 to HFFFF 3 Binary number Example B0010 B1111 Valid range B0000000000000000 to B1111111111111111 4 Types of constant The types of constants are specified by putting symbols after constant...

Страница 145: ...n and calculation in the program 2 Meaning of structure flag data type and meanings Format FL1 FL2 Meaning FL1 Posture data It indicates the robot arm posture in the XYZ coordinates FL2 Multiple rotation data It includes information of the rotational angle of each joint axis at the position XYZ and posture ABC expressed as XYZ coordinates Default value 0 The range is 0 to 4294967295 Information fo...

Страница 146: ... the J3 axis of a horizontal multi joint type robot is a direct driven axis 900 540 180 0 180 540 900 2 E 1 F 0 1 2 Value of multiple rotation data Angle of each axis Value of multiple rotation data Designation of axis No 1 There is no need to describe the coordinate and posture data for all eight axes However if omitted the following axis data will be processed as undefined For a 4 axis robot X Y...

Страница 147: ... and user defined external variable valid over programs The user defined external variable has a _ for the second character of the variable name Refer to Page 137 4 3 22 External variables for details Use of variables in joint element data The axis data is called the joint element data A variable cannot be contained in the joint constant data that configures the joint constant Note 1 Numeric value...

Страница 148: ...ed during a single precision double precision execution an error will occur Table 4 5 Range of numeric value variable data 4 3 17 Character string variables A character string variable should start with C and end with If it is defined by the Def Char instruction it is possible to specify a name beginning with a character other than C Example C1 ABC CS C1 Def Char MOJI MOJI MOJIMOJI 4 3 18 Position...

Страница 149: ...osition variables and joint variables can all be used in arrays Designate the array elements at the subscript section of the variables Array variables should be declared with the Dim instruction It is possible to use arrays of up to three dimensions Example Example of definition of an array variable Dim M1 10 Single precision real number type Dim M2 10 Integer type Dim M3 10 Single precision real ...

Страница 150: ...rogram P_GENTEN M_MACHI Robot status variables System status variables The robot status variables are controlled by the system and their usage is determined in advance M_In M_Out P_Curr M_PI etc Data type Variable name Qty Remarks Position P_00 to P_19 P_20 to P_39 Note 20 20 Position array No of elements 10 P_100 to P_104 P_105 to P_109 Note 5 5 Use the array element in the first dimensions Joint...

Страница 151: ...am in which they will be used It is not necessary to declare local variables variables valid only within programs again Example Example of using user defined external variables On the main program program name 1 side On the user base program program name UBP side Procedure before using user defined external variables 1 First write a user base program Use _ for the second character of the variables...

Страница 152: ...y the Instructions check box is checked 4 When the copy operation is complete perform the operation in step 3 above again Uncheck the Instructions check box and check the Position Variables check box this time and then execute 5 Write a user base program in the robot controller first when deleting a program and then register it again in the program management window as well What is a user base pro...

Страница 153: ... 1 to 3 Currently designated base conversion data R Position type 302 12 P_NTool Mechanism No 1 to 3 System default value tool conversion data R Position type 306 13 P_NBase Mechanism No 1 to 3 System default value base conversion data R Position type 302 14 M_Tool Mechanism No 1 to 3 Tool No 1 to 4 RW Integer type 295 15 J_ColMxl Mechanism No 1 to 3 Difference between estimated torque and actual ...

Страница 154: ...r type 290 39 M_Wai Slot No 1to 32 Pause status 1 Pausing 0 Not pausing R Integer type 298 40 M_Psa Slot No 1to 32 Specifies whether or not the program selection is possible in the specified task slot 1 Selection possible 0 Selection not possible in pause status R Integer type 289 41 M_Cys Slot No 1to 32 Cycle operation status 1 Cycle operation 0 Non cycle operation R Integer type 277 42 M_Cstp No...

Страница 155: ...nput No from 6000 CC Link s remote register Input register R Integer type 278 60 M_DOut Output No from 6000 CC Link s remote register output register RW Integer type 278 61 M_HndCq Input No 1 to 8 Returns a hand check input signal R Integer type 281 62 P_Safe Mechanism No 1 to 3 Returns an safe point position R Position type 305 63 J_Origin Mechanism No 1 to 3 Returns the joint coordinate data whe...

Страница 156: ...TO Ext 1 2 3 R Integer type 285 Note1 Mechanism No 1 to 3 Specifies a mechanism number corresponding to the multitask processing function Slot No 1 to 32 Specifies a slot number corresponding to the multitask function Input No 0 to 32767 theoretical values Specifies a bit number of an input signal Output No 0 to 32767 theoretical values Specifies a bit number of an output signal Note2 R Only readi...

Страница 157: ...s into an integer 313 Deg Numeric expression radian Converts the angle unit from radian rad to degree deg 316 Exp Numeric expression Calculates the value of the expression s exponential function 317 Fix Numeric expression Produces an integer section 318 Int Numeric expression Produces the largest integer that does not exceed the value in the expression 320 Len Character string expression Produces ...

Страница 158: ...alue Position vari ables Dist Position Position Obtains the distance between two points 317 Position Fram Position 1 Position 2 Position 3 Calculates the coordinate system designated with three points Position 1 is the plane origin position 2 is the point on the X axis and position 3 is the point on the Y axis direction plane The plane origin point and posture are obtained from the XYZ coordinates...

Страница 159: ...thin the movement range 327 Numeric value PosMid Position1 Position2 Numeric value1 Numeric value2 Calculates the middle position between position 1 and position 2 328 Position CalArc Position 1 Position 2 Position 3 Numeric value1 Numeric value2 Numeric value3 Position 4 Returns information of an arc created from position 1 position 2 and position 3 312 Numeric value SetJnt J1 axis J2 axis J3 axi...

Страница 160: ...sition Tool Specification of compliance in the Tool coordinate system 167 Cmp Off Composition OFF Compliance setting invalid 169 CmpG Composition Gain Compliance gain specification 170 Oadl Optimal Acceleration Optimum acceleration deceleration rate specification 229 Loadset Load Set Hand s optional condition specification 213 Prec Precision High accuracy mode specification 237 Torq Torque Torque ...

Страница 161: ...t definition 179 Act Act Starts or ends interrupt monitoring 155 Def Arch Define arch Definition of arch shape for arch motion 182 Def Jnt Define Joint Joint type position variable definition 188 Def Pos Define Position XYZ type position variable definition 191 Def Inte Def Long Def Float Def Double Define Integer Long Float Double Integer or real number variable definition 185 Def Char Define Cha...

Страница 162: ...4 149 List of Instructions 4MELFA BASIC IV 5 Others Command Explanation Page ChrSrch Character search Searches the character string out of the character array 160 Get Pos Get Position Reserved ...

Страница 163: ...Integer Integer Addition Substract Multiplication Division Integer division Remainder MOD Exponent Substitution Comparison Compari son operators Logic Logic operators Integer Integer Integer Integer Integer Integer Integer Integer Integer Integer Real number Real number Real number Real number Integer Integer Integer Integer Integer Integer Real number Addition Substract Multiplication Division In...

Страница 164: ...l deeper Each command has a limit to the depth of the control structure Exceeding these limits will cause an error Table 4 13 Limit to control structure depth 4 10 Reserved words Reserved words are those that are already used for the system A name that is the same as one of the reserved words cannot be used in the program Instructions functions and system status variables etc are considered reserv...

Страница 165: ...s that a space is required Terminology Indicates the meaning and range etc of the argument Reference Program Indicates a program example Explanation Indicates detailed functions and cautions etc The available robot type Indicates the available robot type Related parameter Indicates the related parameter Related system variables Indicates the related system variables Related instructions Indicates ...

Страница 166: ...te when moving upward in an arch motion due to the Mva instruction Adefaultvalueof100issetiftheargumentisomitted Itispossibletospecifytheargument either by a constant or variable Acceleration Deceleration rate when moving downward Specifytheacceleration decelerationratewhenmovingdownwardinanarchmotiondue to the Mva instruction Adefaultvalueof100issetiftheargumentisomitted Itispossibletospecifythea...

Страница 167: ...the acceleration deceleration time is set to more than 100 it may affect the lifespan of the machine In addition speed over errors and overload errors may tend to occur Therefore be extra careful when you are setting it to more than 100 4 The smooth operation when Cnt is valid will have a different locus according to the acceleration speed or operation speed To move smoothly at a constant speed se...

Страница 168: ... When the input signal 1 turns on set to 1 while moving from P1 to P2 it loops until that signal is set to 0 1 Def Act 1 M_In 1 1 GoSub INTR Assign input signal 1 to the interrupt 1 condition 2 Mov P1 3 Act 1 1 Enable interrupt 1 4 Mov P2 5 Act 1 0 Disable interrupt 1 10 INTR 11 IF M_In 1 1 GoTo 110 Loops until the M_In 1 signal becomes 0 12 Return 0 2 When the input signal 1 turns on set to 1 whi...

Страница 169: ...e done by describing either RETURN 0 or RETURN 1 How ever when returning from interruption processing to the next step by RETURN1 execute the statement to disable the interrupt When that is not so if interruption conditions have been satisfied because interrup tion processing will be executed again and it will return to the next step the step may be skipped 5 Even if the robot is in the middle of ...

Страница 170: ... Distance to move parallel to Y axis Z Distance to move parallel to Z axis A Angle to turn toward the X axis B Angle to turn toward the Y axis C Angle to turn toward the Z axis L1 Movement amount of additional axis 1 L2 Movement amount of additional axis 2 1 For A B and C the clockwise direction looking from the front of the origin of the coordinate used as the center of rotation is the forward ro...

Страница 171: ... 1 When passing the argument to the program to call Main program 1 M1 0 2 CallP 10 M1 P1 P2 3 M1 1 4 CallP 10 M1 P1 P2 10 CallP 10 M2 P3 P4 15 End 100 sub program side 100 FPrm M01 P01 P02 101 If M01 0 Then GoTo LBL1 102 Mov P01 103 LBL1 104 Mvs P02 105 End Return to the main program at this point When step 2 and 4 of the main program are executed M1 P1 and P2 are set in M01 P01 and P02 of the sub...

Страница 172: ...Plt and Dim instructions executed in the main program are invalid in a program called by the CallP instruction They become valid when the control is returned to the main program from the program called by the CallP instruction again 6 Speed and tool data are all valid in a sub program Values of Accel and Spd are invalid The mode of Oadl is valid 7 Another sub program can be executed by calling Cal...

Страница 173: ...ables and the element number of the completely matched character string array is set in search result storage destination Partially matched character strings are not searched Even if ChrSrch C1 1 ROBO M1 are described in the above statement example the matched character string is not searched 2 If the character string to be searched is not found 0 is set in search result storage destination 3 Char...

Страница 174: ...ushed The data left in the buffer will be processed as follows when the file is closed Table 4 14 Processing of each buffer when the file is closed 2 Executing an End statement will also close a file 3 If the file number is omitted all files will be closed Related instructions Open Open Print Print Input Input Close File No File No Buffer types Processing when the file is closed Communication line...

Страница 175: ...susedintheprogramarecleared to zero 3 Clears all external numerical variables External system variables and user defined external variables andexternalnumericalarrayvariables settingthemto0 External position variables are not cleared Reference Program 1 The general purpose output signal is output based on the output reset pattern 1 Clr 1 2 The local numeric variables and numeric array variables in...

Страница 176: ...ow do not function if this servo free equivalent behavior is in use 3 The soft state is maintained even after the robot program execution is stopped To cancel the soft status execute the Cmp Off command or turn Off the power 4 When pressing in the soft state the robot cannot move to positions that exceed the operation limit of each joint axis 5 If the amount of difference between the original targ...

Страница 177: ...e is used the robot may operate in a direction different from the expected moving direction because the directions of the coordinate systems con trolled by the jog operation and the compliance mode differ When performing the teaching of a position while in the compliance mode perform servo OFF first Be careful that if teaching operation is performed with Servo ON the original com mand position is ...

Страница 178: ... of the command position and actual position can be read with M_CmpDst The success failure of pin insertion can be checked using this variable 6 If the amount of difference between the original target position and the actual robot position becomes greater than 200 mm by pushing the hand etc the robot will not move any further and the operation shifts to the next step of the program 7 It is not pos...

Страница 179: ...Cmp Pos instruction use the XYZ jog mode If any other jog mode is used the robot may operate in a direction different from the expected moving direction because the directions of the coordinate systems con trolled by the jog operation and the compliance mode differ When performing the teaching of a position while in the compliance mode perform servo OFF first Be careful that if teaching operation ...

Страница 180: ... the power 5 When pressing in the soft state the robot cannot move to positions that exceed the operation limit of each joint axis 6 The deviation of the command position and actual position can be read with M_CmpDst The success fail ure of pin insertion can be checked using this variable 7 If the amount of difference between the original target position and the actual robot position becomes great...

Страница 181: ... or the power is turned off Exercise caution when changing the executable program number or operating the jog To execute a jog operation after setting the compliance mode with the Cmp Tool instruction use the Tool jog mode If any other jog mode is used the robot may operate in a direction different from the expected moving direction because the directions of the coordinate systems con trolled by t...

Страница 182: ...tion 5 M_Out 10 1 Instructs to close the chuck for positioning 6 Dly 1 0 Waits for the completion of chuck closing 1 sec 7 HOpen 1 Open the hand 8 Mvs 100 Retreats 100 mm in the Z direction of the Tool coordinate sys tem 9 Cmp Off Return to normal state Explanation 1 This instruction cancels the compliance mode started by the Cmp Tool Cmp Pos or Cmp Jnt instruction 2 In order to cancel jog operati...

Страница 183: ...be generated in proportion to the deviation of the command position and actual position CmpG designates that spring constant 4 The deviation of the command position and actual position can be read with M_CmpDst The success failure of pin insertion can be checked using this variable 5 If a small gain is set and the soft state is entered with the Cmp Pos Cmp Tool and Cmp Jnt commands the robot posit...

Страница 184: ...inuous movement 5 Cnt 1 100 200 Continuous operation specification at 100 mm on the starting side and at 200 mm on the end side 6 Mvs P3 Continuous operation at a specified distance before and after an interpolation 7 Cnt 1 300 Continuous operation specification at 300 mm on the starting side and at 300 mm on the end side 8 Mov P4 Continuous operation specification at 300 mm on the starting side 9...

Страница 185: ...om the target position but the operating time will be the short est To pass through a location closer to the target position set this neighborhood distance numerical value 1 numerical value 2 Fig 4 8 Setting Up the Neighborhood Distance 10 MOV P1 20 MVS P2 30 MOV P3 It decelerates and accelerates to P1 P2 and P3 After moving to the target position it moves to the next target position 10 CNT 1 20 M...

Страница 186: ...ame value as numeric value 1 will be applied 8 When continuous operation is specified the positioning completion specification by the Fine instruction will be invalid 9 If the proximity distance value 1 value 2 is set small the movement time may become longer than in the status where Cnt 0 10 Even when continuous operation is specified acceleration deceleration is performed for the interpola tion ...

Страница 187: ...COlLvl 80 80 80 80 80 80 Specify the allowable level for impact detection 2 ColChk On Enable the impact detection function 3 Mov P1 4 Mov P2 5 Dly 0 2 Wait until the completion of operation Fine instruction can also be used 6 ColChk Off Disable the impact detection function 7 Mov P3 Reference Program 2 If interrupt processing is used in the case of impact 1 Def Act 1 M_ColSts 1 1 GoTo HOME S Defin...

Страница 188: ...th the interrupt condition of M_ColSts 1 and denotes a machine number is not enabled when specifying NOErr error non occurrence mode See Syntax Example 2 Error 3960 also occurs if this interrupt processing is disabled while in the error non occurrence mode 8 If an impact is detected while in the error non occurrence mode the robot turns OFF the servo and stops Therefore no error occurs and operati...

Страница 189: ... is enabled by this instruction the execution time tact time may become long for some programs Use the impact detection function only for operations that may interfere with peripheral devices rather than enabling it for the entire program 14 This function cannot be used together with the multi mechanism control function Related instructions and variables ColLvl Col Level M_ColSts J_ColMxl P_ColDir...

Страница 190: ...xes 100 is set as the initial value of the ColLvl parameter 5 If this value is increased the detection level sensitivity lowers if this value is lowered the detection level increases 6 If the detection level is increased the probability of erroneous detection becomes high Adjust the level such that it does not become too high Depending on the posture and operation speed erroneous detection may als...

Страница 191: ...ed to the communication line If the argument is omitted 1 is set as the default value Reference Program Refer to Page 231 On Com GoSub ON Communication Go Subroutine Explanation 1 When Com On Off is executed even if communications are attempted the interrupt will not be gener ated 2 For information on communication line Nos refer to the Page 234 Open Open 3 After Com Stop is executed even if commu...

Страница 192: ...on of the external override If the external override is small the time required for the robot to stop becomes longer but it will always stop at the same position S Stop type 2 The robot decelerates and stops in the shortest time and distance possible independently of the external override L Execution complete stop The interrupt processing is performed after the robot has moved to the target positi...

Страница 193: ...than any of the interrupts defined by Def Act 7 Def Act definitions are valid only in the programs where they are defined These are invalid when called up in a program by CallP If necessary the data in a sub program may need to be redefined 8 If an interrupt is generated when a GoTo command is designated by Process for a Def Act command during execution of the remaining program the interrupt in pr...

Страница 194: ...5 Conceptual diagram showing the effects of different stop commands Related instructions Act Act External override 100 maximum speed External override 50 Stop type 1 If the argument is omitted S1 S2 Stop type 2 S Execution com plete stop L S3 S4 Speed Time Interrupt Stop distance S1 Time Speed Interrupt Stop distance S2 Speed Time Interrupt Speed Time Interrupt Decelerate and stop immediately Spee...

Страница 195: ...pe definition in step 10 3 Mva P2 2 The robot moves according to the default values specified by the parameters Explanation 1 If the Mva instruction is executed without the Def Arch instruction the robot moves according to the arch shape specified by the parameters 2 Used to change the increments in a program etc Related instructions Mva Move Arch Accel Accelerate Ovrd Override Mvs Move S Used as ...

Страница 196: ...RKSET in the MESSAGE variable 3 CMSG ABC Substitute ABC for variable CMSG For variables starting with C the definition of Def Char is not required Explanation 1 The variable name can have up to eight characters Refer to the Page 129 4 3 6 Types of characters that can be used in program for the characters that can be used 2 When designating multiple variable names the maximum value 127 characters i...

Страница 197: ...Explanation 1 FN Name becomes the name of the function The function name can be up to 8 characters long Example Numeric value type FNMMAX Identification character M Character string type FNCAME Identification character C Describe at the end of the name 2 A function defined with Def FN is called a user defined function A function as long as one step can be described 3 Built in functions and user de...

Страница 198: ...468000 is set to WORK3 4 Definition of the double precision type real number variable 1 Def Double WORK4 2 WORK4 100 3 Numerical 33 333332061767599 is set to WORK4 Explanation 1 The variable name can have up to eight characters Refer to the Page 129 4 3 6 Types of characters that can be used in program for the characters that can be used 2 When designating multiple variable names the maximum value...

Страница 199: ...put variable named PORT1 to input output signal number 6 in bit type 1 Def IO PORT1 BIT 6 10 PORT1 1 Output signal number 6 turns on 20 PORT1 2 Output signal number 6 turns off Because the lowest bit of the numerical value 2 is 0 21 M1 PORT1 Substitute the state of the input signal number 6 for M11 2 Assign the input variable named PORT2 to input output signal number 5 in byte type and specify the...

Страница 200: ...an be used 5 When mask information is designated only the specified signal will be validated Example In the above example on the 20th step the input output data with a bit width of eight is masked by 0F in hexadecimal Thus if PORT 2 is used thereafter When used as an input signal M1 PORT 2 Numbers 5 to 8 are used for input and numbers 9 to 12 are always treated as 0 No 12 No 5 Input output bit No ...

Страница 201: ...tion of Def Jnt is not required 3 SAFE 50 120 30 300 0 0 0 0 4 Mov SAFE Move to SAFE Explanation 1 Use this instruction to define a joint position variable by a name beginning with a character other than J 2 The variable name can have up to eight characters Refer to the Page 129 4 3 6 Types of characters that can be used in program for the characters that can be used When designating multiple vari...

Страница 202: ...n 3 Arc pallet posture equal division 11 Zigzag posture fixation 12 Same direction posture fixation 13 Arc pallet posture fixation Reference Program 1 Def Plt 1 P1 P2 P3 4 3 1 Define a 3 point pallet 2 Def Plt 1 P1 P2 P3 P4 4 3 1 Define a 4 point pallet Explanation 1 The accuracy of the position calculation will be higher for a 4 point pallet than for a 3 point pallet 2 The command is valid only w...

Страница 203: ...ure components are close to 180 degrees please read Precautions on the posture of position data in a pallet definition in Page 98 4 1 2 Pallet operation The value of the start point of the pallet definition is employed for the structure flag of grid points FL1 of position data calculated during pallet operation Plt instruc tion For this reason if position data with different structure flags are us...

Страница 204: ...on of Def Pos is not required 3 WORKSET 250 460 100 0 0 90 0 0 0 0 4 Mov WORKSET Move to WORKSET Explanation 1 Use this instruction to define a XYZ type position variable by a name beginning with a character other than P 2 The variable name can have up to eight characters Refer to the Page 129 4 3 6 Types of characters that can be used in program for the characters that can be used 3 When designat...

Страница 205: ...rt from 1 when actually referencing array variables For PDATA on step 10 of the statement example the element number will be 1 to 10 4 Eelement Value can be described with numeric constants from 1 to 999 It is not allowed to use a numerical value operation expression If the number of elements is specified using a real number an integer with rounded decimal part will be assumed Depending on the sys...

Страница 206: ...s positioning movement instructions and for specifying pulse output times when used in a signal output statement such as step 20 in statement example above 2 The pulse output will be executed simultaneously as the next command in the steps that follow 3 Up to 50 pulse outputs can be issued of all programs simultaneously Exceeding this an error will occur when the program tries to execute it 4 A pu...

Страница 207: ...id dle and put it in the pause status 2 If executed from the operation panel a program is executed in the continuos operation mode it will be executed again from the top even if it contains an End instruction If it is desired to end a program at the End instruction press the End key on the operation panel to stop the cycle 3 It is allowed to have several End statements within one program 4 The End...

Страница 208: ...f a LOW level or HIGH level error is generated the program is paused Steps after the Error instruction are not executed A CAUTION error does not pause a program the next step and onward are executed The action of system by error number is shown in the Table 4 16 3 It is possible to create up to 20 error messages using parameters UER1 to UER20 4 A system error occurs if a value outside the error nu...

Страница 209: ... instruction timer is used for positioning instead of the Fine instruction This instruction is easier to specify 10 Mov P1 20 Dly 0 1 3 Fine is invalid in the program until the Fine command is executed Once Fine is validated it remains valid until invalidated 4 Fine is invalidated at the end of the program Execution of the End instruction program reset after paus ing 5 When the continuous movement...

Страница 210: ...e instruction is the same the RV S RH S series which normally has higher encoder resolution number of pulses takes longer to complete posi tioning For this reason if robots are replaced and the robot model is changed from the RV A RH A series to the RV S RH S series the time it takes for the Fine instruction to complete positioning may change In such cases adjust the value of No of pulses of the F...

Страница 211: ...ined with a joint value resulting in more accurate positioning 2 The Fine J command deems the operation to be complete when the difference between the command joint position and feedback joint position for all enabled axes is within the Positioning Width 3 Furthermore there are also times when positioning is performed with a Dly command timer instead of the Fine J command This is easier to specify...

Страница 212: ...he command pulse and feedback pulse is within the Linear Distance 3 Furthermore there are also times when positioning is performed with a Dly command timer instead of the Fine P command This is easier to specify 1 Mov P1 2 Dly 0 1 4 Fine P is disabled for all axes by default Once Fine P is enabled the enabled status is applied continuously until disabled 5 Fine P is disabled when a program is term...

Страница 213: ... numeric variable M2 4 MBOX M1 M2 M1 M2 Substitute the value of M1 M2 for the array variable MBOX M1 M2 5 Next M2 Return to step 3 6 Next M1 Return to step 2 Explanation 1 It is possible to describe For Next statements between other For Next statements Jumps in the program caused by the For Next instruction will add one more level to the control structure in a program It is possible to make the co...

Страница 214: ...allP 100 M1 P2 P3 It can be described like CallP 100 1 P_Curr P100 also Sub program 100 1 FPrm M1 P1 P2 2 If M1 1 Then GoTo 40 3 Mov P1 4 Mvs P2 5 End Return to the main program Explanation 1 FPrm is unnecessary if there are no arguments in the sub program that is called up 2 An error occur when the type or number is different between the argument of CallP and the dummy argu ment that defined by F...

Страница 215: ...F 7 RelM Releases the control right of mechanism 1 8 End Explanation 1 Normally in single task operation mechanism 1 is obtained in the initial status it is not necessary to use the GetM instruction 2 Because the control right of the same mechanism cannot be acquired simultaneously by multiple tasks the following procedure is required in order to operate the robot by other than slot 1 First releas...

Страница 216: ...use the Return instruction to return Explanation 1 Make sure to return from the subroutine by using the Return command If return by GoTo command the memory for control structure stack memory will decrease and it will cause the error at continuous exe cuting 2 The call of other subroutines is possible again by the GoSub command out of the subroutine This approach can be employed approximately up to...

Страница 217: ...m branch to the specified label step unconditionally Format Terminology Branch Destination Describe the label name Reference Program 10 GoTo LBL Branches to the label LBL 100 LBL 101 Mov P1 Explanation 1 If a branch destination or label does not exist an error will occur during execution GoTo Branch Destination ...

Страница 218: ... P1 WthIf M_In 17 1 Hlt When the input signal 17 turns on during moving to P1 the pro gram execution is stopped Explanation 1 Interrupts the execution of a program and decelerates the robot to a stop The system will enter the wait ing state 2 If the Hlt instruction is used in multitask operation only the task slot that executed the Hlt instruction is paused 3 To restart start the O P or issue the ...

Страница 219: ...orceas a constant or variable It can be set in the range of 0 00 sec to the maximum single precision real number The default value is 0 3 sec Reference Program 1 HOpen 1 Open hand 1 2 Dly 0 2 Set the timer to 0 2 sec Wait for the hand to open securely 3 HClose 1 Close hand 1 4 Dly 0 2 Set the timer to 0 2 sec Wait for the hand to close securely 5 Mov PUP Explanation 1 The operation single double o...

Страница 220: ... M_In M_Inb M_Inw 900s number M_Out M_Outb M_Outw 900s number M_HndCq Related instructions Loadset Load Set Oadl Optimal Acceleration Related parameter HANDTYPE HANDINIT Refer to Page 369 5 10 Automatic return setting after jog feed at pause and Page 373 5 13 About default hand status ...

Страница 221: ...e contained in one step 2 It is allowed to split an If Then Else EndIf block over several steps 3 Else can be omitted 4 Make sure to include the EndIf statement in the If Then Else EndIf block 5 If the GoTo instruction is used to jump out from inside an If Then Else EndIf block an error will occur when the memory for control structure stack memory becomes insufficient 6 For If Then Else EndIf it i...

Страница 222: ... as delimiters 4 When the Input statement is executed the status will be standby for input The input data will be substi tuted for the variables at the same time as the carriage return CR and LF are input 5 If the protocol in the case of the standard port the CRPC232 parameter is 0 of the specified port is for PC support non procedure it is necessary to attach PRN at the head of any data sent from...

Страница 223: ...int interpolation 2 The actual override is Operation panel T B override setting value x Program override Ovrd com mand x Joint override JOvrd command The JOvrd command changes only the override for the joint interpolation movement 3 The 100 Designate override is the maximum capacity of the robot Normally the system default value M_NOvrd is set to 100 The value is reset to the default value when th...

Страница 224: ...heoriginforthedesignatedaxisisresetatthevaluedesignatedinparameterJRCORG This can be used only for the user defined axis Axis No The target axis is specified with the number The priority axes are used if omitted Notethatthisargumentcannotbeomittedifadditionalaxesand oruser definedmechan ical axes are the targets Applicable Models and Applicable Axes 1 Applicable models and priority axes 2 Addition...

Страница 225: ...defined mechanism Set the origin position for executing JRC 0 with JRCORG Only for the additional axis or user defined mechanism 8 When parameter JRCEXE is set to 0 no process will take place even if JRC command is executed 9 If the movement amount designated with parameter JRCQTT is not within the pulse data 0 to Max an error will occur during the initialization Here Max is 2 Number of encoder bi...

Страница 226: ...nd when the program execution starts 3 Set the weight size X Y Z and center of gravity position X Y Z as the hand conditions in parameter HNDDAT 1 to 8 4 Set the weight size X Y Z and center of gravity position X Y Z as the workpiece conditions in parameter WRKDAT 1 to 8 5 The hand conditions and workpiece conditions changed when this command is executed are reset to the system default value when ...

Страница 227: ...rpolation amount 4 Detour refers to the operating exactly according to the teaching posture Short cut operation may take place depending on the teaching posture 5 Short cut operation refers to posture interpolation between the start point and end point in the direction with less motion 6 The detour short cut designation is significant when the posture axis has a motion range of 180 deg or more 7 E...

Страница 228: ...nstant or a joint variable Arch number A number defined by the Def Arch instruction 1 to 4 If the argument is omitted 1 is set as the default value Reference Program 1 Def Arch 1 5 5 20 20 Defines the arch shape configuration 2 Ovrd 100 20 20 Specifies override 3 Accel 100 100 50 50 50 50 Specifies acceleration deceleration rate 2 Mva P1 1 Performs the arch motion movement according to the shape c...

Страница 229: ... execution of a Mva instruction and restarted after jog feed the robot returns to the inter rupted position and restarts the Mva instruction this can be changed by the RETPATH parameter The interpolation method JOINT interpolation XYZ interpolation which returns to the interrupted posi tion can be changed by the RETPATH parameter Refer to Page 369 5 10 Automatic return setting after jog feed at pa...

Страница 230: ...e is moved 360 degrees 2 The posture at the starting point is maintained during circle interpolation The postures while passing points 1 and 2 are not considered 3 If the current position and the starting position do not match the robot automatically moves to the start ing point based on the linear interpolation 3 axis XYZ interpolation and then performs the circle inter polation 4 If paused durin...

Страница 231: ...noperationexpressionorjointoperation expression End Point End point for the arc Describe a position operation expression or joint operation expression Constants 1 Short cut detour 1 0 The default value is 0 Constants 2 Equivalent rotation 3 axis XYZ singular point passage 0 1 2 The default value is 0 Appended conditions The Wth and WthIf statements can be used Reference Program 1 Mvr P1 P2 P3 2 Mv...

Страница 232: ...e RETPATH parameter Refer to Page 369 5 10 Automatic return set ting after jog feed at pause 5 If the start point and end point structure flags differ when equivalent rotation constant 2 0 is specified an error will occur at the execution 6 Of the three designated points if any points coincide with the other or if three points are on a straight line linear interpolation will take place from the st...

Страница 233: ... point for the arc This position may be specified using a position type variable and constant or a joint variable Reference point Reference point for a circular arc This position may be specified using a position type variable and constant or a joint variable Constants 1 Short cut detour 1 0 The default value is 0 Constants 2 Equivalent rotation 3 axis XYZ singular point passage 0 1 2 The default ...

Страница 234: ...ause 5 The direction of movement is in a direction that does not pass through the reference points 6 If the start point and end point structure flags differ when equivalent rotation constant 2 0 is specified an error will occur at the execution 7 Of the three designated points if any points coincide with the other or if three points are on a straight line linear interpolation will take place from ...

Страница 235: ...ay be specified using a position type variable and constant or a joint variable Center Point Centerpointforthearc Thispositionmaybespecifiedusingapositiontypevariable and constant or a joint variable Constants 1 Short cut detour 1 0 The default value is 0 Constants 2 Equivalent rotation 3 axis XYZ singular point passage 0 1 2 The default value is 0 Appended conditions The Wth and WthIf statements ...

Страница 236: ...will occur at the execution 6 If 3 axis XYZ is designated for the constant 2 the constant 1 will be invalidated and the robot will move with the taught posture 7 Constant 2 designates the posture interpolation type 3 axis XYZ is used when carrying out interpolation on the X Y Z J4 J5 J6 coordinate system and the robot is to move near a particular point 8 The central angle from the start point to t...

Страница 237: ... can be used Separation Distance When this value is designated the axis will move the designated distance fromthecurrentpositiontotheZaxisdirection direction ofthetoolcoor dinate system Reference Program 1 Move to the target position P1 by XYZ interpolation 1 Mvs P1 2 Turns on the output signal 17 at the same time if it moves to the target position P1 by linear interpolation 1 Mvs P1 100 0 Wth M_O...

Страница 238: ...ted position and restarts the Mvs instruction This can be changed by the RETPATH parameter and also the interpolation method JOINT interpolation XYZ interpolation which returns to the inter rupted position can be changed by same parameter Some robots for liquid crystal transportation have different default values of this parameter Refer to Page 369 5 10 Automatic return setting after jog feed at p...

Страница 239: ...vs should be used if it is desired to perform linear interpolation based on such posture coordinates Note that strictly speaking this 3 axis XYZ method does not maintain the postures as it evenly interpolates the joint angle of axes J4 J5 and J6 at pos ture A and C Therefore it is expected that the robot hand s pos ture may move forward and backward while moving from posture A to posture C In this...

Страница 240: ...ON 3 The operating characteristics mode returns to standard mode when a program is terminated End command execution program reset following an interruption however the current operating characteristics mode is retained with the sub program End command executed with the CallP command 4 The current operating characteristics mode is retained when restarting after a program interruption including inte...

Страница 241: ... With high speed positioning mode the vibration level when decelerating and stopping is sometimes greater when compared to standard mode Select standard mode if there is any interference 9 Trajectory priority mode has been adjusted so that the optimum effect is obtained with operating speeds in the mid to low speed range Consequently when performing an operation such as drawing a small circle at h...

Страница 242: ...HClose 1 8 Mov P4 Move with hand 1 workpiece 1 load 9 Oadl Off When parameter HNDHOLD1 is set to 0 1 Explanation 1 The robot moves with the optimum acceleration deceleration according to the hand conditions and work piece conditions designated with the LoadSet command 2 The workpiece grasp not grasp for when the hand is opened or closed is set with parameter HNDHOLD 1 to 8 3 Initial setting of Oad...

Страница 243: ...4 230 Fig 4 17 Acceleration deceleration pattern at light load Related instructions Accel Accelerate Loadset Load Set HOpen HClose Hand Open Hand Close Related parameter HNDDAT 0 to 8 WRKDAT 0 to 8 HNDHOLD 1 to 8 ACCMODE JADL Speed Time Speed Time OADL ON ...

Страница 244: ...will branch to label RECV 23 24 Com 1 Off Disable interrupt from file No 1 communication line 25 Close 1 26 End 30 RECV Communication interruption processing 31 Input 1 M0001 Set the received information as M0001 and P0001 32 Input 1 P0001 39 Return 1 Returns control to the next step of interrupted step Explanation 1 If the file No is omitted 1 will be used as the file No 2 The file Nos with the s...

Страница 245: ... 42 43 Return Be sure to return by using Return Explanation 1 The value of Expression determines which step label subroutine to call For example if the value of Expression is 2 the step label described for the second value is called 2 If the value of expression is larger than the number of destinations called up the program control jumps to the next step For example the program control jumps to th...

Страница 246: ... 30 LJMP When M1 2 31 Describes processing when M1 2 32 40 L67 41 Describes processing when M1 6 or M1 7 42 50 L2 51 Describes processing when M1 3 M1 4 or M1 5 52 Explanation 1 This is the GoTo version of On GoSub 2 If the value of expression is larger than the number of destinations called up the program control jumps to the next step For example the program control jumps to the next step if the...

Страница 247: ... No 1 20 Mov P_01 2 Mov P_01 3 Print 1 P_Curr Output current position to external source 100 00 200 00 300 00 400 00 7 0 format 40Input 1 M1 M2 M3 Receive from external source with 101 00 202 00 303 00 AscII for mat 5 P_01 X M1 6 P_01 Y M2 7 P_01 C Rad M3 Copy to global data 8 Close Close all opened files 9 End 2 File operation Create the file temp txt to the controller and write abc 1 Open temp t...

Страница 248: ...nt interpolation Operation panel T B override setting value x Program override Ovrd com mand x Joint override JOvrd command During linear interpolation Operation panel T B override setting value x Program override Ovrd com mand x Linear designated speed Spd command 3 The Ovrd command changes only the program override 100 is the maximum capacity of the robot Normally the system default value M_NOvr...

Страница 249: ...ition 22 Mov PLACE 50 Moves 50 mm above the pallet top mount position 23 Ovrd 50 24 Mvs PLACE 25 HOpen 1 Open the hand 26 Dly 0 5 27 Ovrd 100 28 Mvs 50 Moves 50 mm above the current position 29 M1 M1 1 Add the counter 30 If M1 12 Then LOOP If the counter is within the limits repeats from LOOP 31 Mov PICK 50 32 End Explanation 1 The position of grid of a pallet defined by the Def Plt statement is o...

Страница 250: ... is enabled using the Prec On instruction if it is desired to perform interpolation movement with increased path accuracy 2 When this instruction is used the path accuracy is improved but the program execution time tact time may become longer because the acceleration deceleration times are changed internally 3 The enabling disabling of the high accuracy mode is activated from the first interpolati...

Страница 251: ...put format of data reference The output space for the value for Expression and for the character string is in units of 14 characters When outputting multiple values use a comma between each Expression as a delimiter If a semicolon is used at the head of each space unit it will output after the item that was last dis played The carriage return code will always be returned after the output data 3 Th...

Страница 252: ...urrent slot to 3 Slot 2 1 Priority 4 Sets the number of executed steps for this slot to 4 Explanation 1 Programs of other slots are not executed until the specified number of steps is executed For example as in the statement example above if Priority 3 is set for slot 1 s program and Priority 4 is set for slot 2 s program three steps of the slot 1 program are executed first then four steps of the ...

Страница 253: ...2 2 XRun 2 10 Start the program 10 in slot 2 3 Wait M_Run 2 1 Wait for the starting confirmation of the slot 2 Task slot 2 Program 10 1 GetM 1 Get the control of mechanism 1 2 Servo On Turn on the servo of mechanism 1 3 Mov P1 4 Mvs P2 5 Servo Off Turn off the servo of mechanism 1 6 RelM Releases the control right of mechanism 1 7 End Explanation 1 Releases the currently acquired mechanism resourc...

Страница 254: ...nology Comment Describe a user selected character string Descriptions can be made in the range of position steps Reference Program 1 Rem MAIN PROGRAM 2 MAIN PROGRAM 3 Mov P1 Move to P1 Explanation 1 Rem can be abbreviated to be a single quotation mark 2 It can be described after the instruction like an 30 step in reference program Rem Comment ...

Страница 255: ...tantly executed programs Format Reference Program Example of execution in a constantly executed program 1 If M_Err 1 Then Reset Err Resets an error when an error occurs in the controller Explanation 1 This instruction is used in a program whose start condition is set to constant execution ALWAYS by the SLT parameter when it is desired to reset system errors of the robot 2 It becomes enabled when t...

Страница 256: ...Reference Program 1 The example of Return from the usual subroutine 1 MAIN PROGRAM 2 GoSub SUB_INIT Subroutine jumps to label SUB_INIT 3 Mov P1 100 SUB INIT Subroutine 11 SUB_INIT 12 PSTART P1 13 M100 123 14 Return Returns to the step immediately following the step where the subrou tine was called from 2 The example of Return from the subroutine for interruption processing Calls the subroutine on ...

Страница 257: ...insufficient 4 When there is a Return command in a normal subroutine with a return to designation number and when there is a Return command in an interrupt processing subroutine with no return to destination number an error will occur 5 when returning from interruption processing to the next step by Return1 execute the statement to dis able the interrupt When that is not so if interruption conditi...

Страница 258: ...ion expression IS Comparison operator Constant Constant Constant TO Constant Process Writes any instruction other than the GoTo instruction provided by MELFA BASIC V Reference Program 1 Select MCNT 2 M1 10 This line is not executed 3 Case Is 10 MCNT 10 4 Mov P1 5 Break 6 Case 11 MCNT 11 OR MCNT 12 6 Case 12 7 Mov P2 8 Break 9 Case 13 TO 18 13 MCNT 18 10 Mov P4 11 Break 12 Default Other than the ab...

Страница 259: ...ut processing 3 The Select Case and End Select statements must always correspond If a GoTo instruction forces the program to jump out from a Case block of the Select Case statement the free memory available for control structure stack memory decreases Thus if a program is executed continuously an error will eventually occur 4 If an End Select statement that does not correspond to Select Case is ex...

Страница 260: ...nd describe by constant or variable Reference Program 1 Servo On Servo On 2 L2 3 IF M_Svo 1 GoTo L2 Wait for servo On 4 Spd M_NSpd 5 Mov P1 6 Servo Off Explanation 1 The robot arm controls the servo power for all axes 2 If additional axes are attached the servo power supply for the additional axes is also affected 3 If used in a program that is executed constantly this instruction is enabled by ch...

Страница 261: ...ition variable P1 stop the robot interpolation motion and stop execution of this command and execute the next step 2 If M_SkipCq 1 Then Hlt Pauses the program if the execution is skipped Explanation 1 This command is described with the WHT or WthIf statements In this case the execution of that step is interrupted and control is automatically transferred to the next step Execution of skip can be se...

Страница 262: ...d command 3 The Spd command changes only the linear circular designated speed 4 When M_NSpd The default value is 10000 is designated for the designated speed the robot will always move at the maximum possible speed so the line speed will not be constant optimum speed control 5 An error may occur depending on the posture of the robot despite of the optimal speed control If an excessive speed error ...

Страница 263: ...old personal computer support software Format Terminology Character String Message for title Reference Program 1 Title ROBOT Loader program 2 Mov P1 3 Mvs P2 Explanation 1 Although characters can be registered up to the maximum allowed for each step in the program only a maximum of 20 characters can be displayed in the program list display field of the robot controller using the personal computer ...

Страница 264: ... hands are of the same type the control point should be set by the MEXTL parameter instead of by the Tool instruction 2 The tool conversion data changed with the Tool command is saved in parameter MEXTL and is saved even after the controller power is turned OFF 3 The system default value P_NTool is applied until the Tool command is executed Once the Tool command is executed the designated tool con...

Страница 265: ...rque limit value of the specified axis so that a torque exceeding the specified torque value will not be applied during operation Specify the ratio relative to the standard torque limit value The standard torque limit value is predefined by the manufacturer 2 The available rate of torque limitation is changed by robot type The setting is made for each servo motor axis thus it may not be the torque...

Страница 266: ...ask slot state 3 Wait M_Run 2 1 3 Variable state 4 Wait M_01 100 Explanation 1 This command is used as the interlock during signal input wait and during multitask execution 2 The Wait instruction allows the program control to continue to the next step once the specified condition is met 3 In case the Wait instruction is executed in several tasks at one time in the multitask execution status the pr...

Страница 267: ...ign 3 Print 1 M1 Output the M1 value 4 WEnd Return to the While statement step 1 5 End End the program Explanation 1 The program between the While statement and WEnd statement is repeated 2 If the result of Expression is true not 0 the control moves to the step following the While statement and the process is repeated 3 If the result of Expression is false is 0 then the control moves to the step f...

Страница 268: ...gram 1 Mov P1 Wth M_Out 17 1 Dly M1 2 Simultaneously with the start of movement to P1 the out put signal No 17 will turn ON for the value indicated with the numeric variable M1 two seconds Explanation 1 This command can only be used to describe the additional condition for the movement command 2 An error will occur if the Wth command is used alone 3 The process will be executed simultaneously with...

Страница 269: ...nput signal 17 turns on the robot will stop 1 Mov P1 WthIf M_In 17 1 Hlt 2 If the current command speed exceeds 200 mm s turn on the output signal 17 for the M1 2 seconds 2 Mvs P2 WthIf M_RSpd 200 M_Out 17 1 Dly M1 2 3 If the rate of arrival exceeds 15 during movement to P3 turn on the output signal 1 3 Mvs P3 WthIf M_Ratio 15 M_Out 1 1 Explanation 1 This command can only be used to describe the a...

Страница 270: ... pauses 12 XRst 2 Cancels the pause status of the program of task slot 2 20 XClr 2 Cancels the program selection status of task slot 2 21 End Explanation 1 An error occurs at execution if the specified slot does not select the program 2 If the designated program is being operating an error will occur at execution 3 If the designated program is being pausing an error will occur at execution 4 If th...

Страница 271: ...ing execute from here Explanation 1 An error occurs at execution if the specified program does not exist 2 If the designated program is already selected for another slot an error will occur at execution 3 If the designated program is being edited an error will occur at execution 4 If the designated program is being executed an error will occur at execution 5 Designate the program name in double qu...

Страница 272: ...Set program execution start step to head step 16 Wait M_Psa 2 1 Wait for program reset to complete 20 XRun 2 Restart 21 Wait M_Run 2 1 Wait for restart to complete Explanation 1 This is valid only when the slot is in the stopped state 2 If used in a program that is executed constantly this instruction is enabled by changing the value of the ALWENA parameter from 0 to 7 and then turning the control...

Страница 273: ... of execution is specified by XLoad command cycle operation 1 XLoad 3 2 Select the program 2 as the slot 3 2 L2 3 If C_Prg 2 1 Then GoTo L2 Wait for load complete 4 XRun 3 1 Start the program 1 with cycle operation Explanation 1 An error occurs at execution if the specified program does not exist 2 If the designated slot No is already in use an error will occur at execution 3 If a program has not ...

Страница 274: ...Reference Program 1 XRun 2 Execute 10 XStp 2 Stop 11 Wait M_WAI 2 1 Wait for stop to complete 20 XRun 2 Restart Explanation 1 If the program is already stopped an error will not occur 2 XStp can also stop the constant execution attribute program 3 If used in a program that is executed constantly this instruction is enabled by changing the value of the ALWENA parameter from 0 to 7 and then turning ...

Страница 275: ... signal 2 M_Out 10 1 Turn on the output signal 10 3 Pulse output of the signal 3 M_Out 17 1 Dly 2 0 Turn on the output signal 17 for 2 seconds Explanation 1 When using this additionally for the pulse output the pulse will be executed in parallel with the execution of the commands on the following steps 2 Be aware that if a pulse is output by M_Outb or M_Outw the bits are reversed in 8 bit units or...

Страница 276: ...t referred to during the program 2 If the same label is defined several times in the same program an error will occur at the execution 3 The reserved words can t be used for the label 4 If the underscore is used for the label name the 1st character is L only If the characters except L are used ex A_LABEL an error occurs Ex The correct example of the label with using the underscore The 1st characte...

Страница 277: ...s can be used in conditional expressions as well as in reference and assignment statements In the format example only reference and assignment statements are given to make the description simple Reference Program An example program using variables is shown Terminology This indicates the meaning and range of an argument Explanation This indicates detailed functions and precautions Reference This in...

Страница 278: ...is variable only reads the data Use the T B to set the date Reference C_Time C_Maker Function This variable returns information on the manufacturer of the robot controller Format Reference Program 1 C1 C_Maker COPYRIGHT1999 is assigned to C1 Explanation 1 This variable returns information on the manufacturer of the robot controller 2 This variable only reads the data Reference C_Mecha Example Char...

Страница 279: ...turns the selected program number name Format Terminology Character String Variable Specify a character string variable to be assigned Numeric 1 to 32 Enter the task slot number If the argument is omitted 1 is set as the default value Reference Program 1 C1 C_Prg 1 10 is assigned to C1 if the program number is 10 Explanation 1 The program number name set loaded into the specified task slot is assi...

Страница 280: ...eads the data 3 Use the T B to set the time Reference C_Date C_User Function This variable returns the data registered in the USERMSG parameter Format Reference Program 1 C1 C_User The characters registered in USERMSG are assigned to C1 Explanation 1 This variable returns the data registered in the USERMSG parameter 2 This variable only reads the data 3 Use the PC support software or the T B to ch...

Страница 281: ...gned Mechanism Number Enter the mechanism number 1 to 3 If the argument is omitted 1 is set as the default value Reference Program 1 J1 J_Curr J1 will contain the current joint position Explanation 1 The joint type variable for the current position of the robot specified by the mechanism number will be obtained 2 This variable only reads the data Reference P_Curr Example Joint Type Variable J_Curr...

Страница 282: ...ce Program 1 M1 100 Set the initial value of the allowable impact level of each axis 2 M2 100 3 M3 100 4 M4 100 5 M5 100 6 M6 100 7 ColLvl M1 M2 M3 M4 M5 M6 Set the allowable impact level of each axis 8 ColChk On Enable the impact detection function Start the calculation of the maximum value of torque error 9 Mov P1 50 ColChk Off Disable the impact detection function End the calculation of the max...

Страница 283: ...iable as shown in the syntax exam ple when using these joint type variables 6 This variable only reads the data Reference ColChk Col Check ColLvl Col Level M_ColSts P_ColDir Available robot type J_ECurr Function Returns the current encoder pulse value Format Terminology Joint Type Variable Specify a joint type variable to be assigned Mechanism Number Enter the mechanism number 1 to 3 If the argume...

Страница 284: ...check the difference between the command value to the servo and the delay in the actual servo 3 J_Fbc can also check if there is a difference as a result of executing a Cmp Jnt instruction 4 This variable only reads the data Reference P_Fbc J_Origin Function Returns the joint data when the origin has been set Format Terminology Joint Type Variable Specify a joint type variable to be assigned Mecha...

Страница 285: ... the ratio of acceleration time set for task slot 1 2 M1 M_DAcl 2 M1 will contain the ratio of deceleration time set for task slot 2 3 M1 M_NAcl M1 will contain the ratio of initial acceleration time value set for task slot 1 4 M1 M_NDAcl 2 M1 will contain the ratio of initial deceleration time value set for task slot 2 5 M1 M_AclSts 3 M1 will contain the current acceleration deceleration status f...

Страница 286: ...kCq variable is referenced even once the Break status is cleared The value is set to zero Therefore to preserve the status save it by substituting it into a numeric variable 4 The Break status is also cleared even if it is referenced on T B monitor screen and so forth M_BTime Function Returns the remaining hour of battery left Unit hour Format Terminology Numeric Variable Specifies the numerical v...

Страница 287: ...o 3 If the argument is omitted 1 is set as the default value Reference Program 1 Mov P1 2 CmpG 0 5 0 5 1 0 0 5 0 5 Set softness 3 Cmp Pos B00011011 Enter soft state 4 Mvs P2 5 M_Out 10 1 6 Mvs P1 7 M1 M_CmpDst 1 M1 will contain the difference between the position specified by the operation command and the actual current position 8 Cmp Off Return to normal state Explanation 1 This is used to check ...

Страница 288: ...0 Enable compliance mode 13 Act 1 1 Enable interrupt 1 14 Mvs P2 15 16 100 Lmt 101 Mvs P1 Movement to P2 is interrupted and returns to P1 102 Reset Err Reset the error 103 Hlt Execution is stopped Explanation 1 This is used to recover from the error status by using interrupt processing if an error has occurred while the command value in the compliance mode attempted to exceed a limit 2 For various...

Страница 289: ... while executing lines 40 through 70 it jumps to interrupt processing 6 Mov P3 7 Mov P4 8 Act 1 0 100 HOME Interrupt processing during impact detection 101 ColChk Off Disable the impact detection function 102 Servo On Turn the servo on 103 PESC P_ColDir 1 2 Create the amount of movement for escape operation 104 PDst P_Fbc 1 PESC Create the escape position 105 Mvs PDst Move to the escape position 1...

Страница 290: ...e The status at this time is returned as 1 2 This variable only reads the data M_Cys Function Returns the status of whether or not a program is on cycle operation 1 In cycle operation operating mode set by the slot parameter SLT to 0 Other than above Format Terminology Numerical variable Specify the numerical variable to substitute Reference Program 1 M1 M_Cys The numerical value 1 is substituted ...

Страница 291: ...the CC Link register number 6000 or above Equation 2 Specifies the CC Link register number 6000 or above Reference Program 1 M1 M_DIn 6000 M1 will contain the CC Link input register value If CC Link station number is 1 2 M1 M_DOut 6000 M1 will contain the CC Link output register value 3 M_DOut 6000 100 Writes 100 to the CC Link output register Explanation 1 For details refer to the CC Link Interfa...

Страница 292: ...dition is set to ALWAYS by the SLT parameter The program set to ALWAYS will not stop even when an error is generated from other programs 2 Level 1 errors are warnings level 2 errors pause programs Level 3 errors pause programs and turn the servo power OFF but error reset can be performed Level 4 errors pause programs turn the servo power OFF and error reset cannot be performed Thus when a level 4 ...

Страница 293: ... interrupt takes effect 3 Torq 3 10 Set the torque limit of the three axes to 10 or less using the torque instruction 4 Mvs P1 Moves 5 End 10 SUB1 11 Mov P_Fbc Align the command position with the feedback position 12 M_Out 10 1 Signal No 10 output 13 Hlt Stop when a difference occurs Explanation 1 This function returns the difference between the command position specified by the operation instruct...

Страница 294: ...HndCq Function Returns the hand check input signal value Format Terminology Numeric Variable Specifies the numerical variable to assign Equation Enter the hand input signal number 1 to 8 Corresponds to input signals 900 to 907 Reference Program 1 M1 M_HndCq 1 M1 will contain the status of hand 1 Explanation 1 Returns one bit of the hand check input signal status such as a sensor 2 M_HndCq 1 corres...

Страница 295: ...input signal 0 1 or 0 2 M2 M_Inb 0 M2 will contain the 8 bit information starting from input signal 0 3 M3 M_Inb 3 AND H7 M3 will contain the 3 bit information starting from input signal 3 4 M4 M_Inw 5 M4 will contain the 16 bit information starting from input signal 5 Explanation 1 Returns the status of the input signal 2 M_Inb and M_Inw will return 8 or 16 bit information starting from the speci...

Страница 296: ... omitted the current slot will be used as the default Reference Program 1 M1 M_Ovrd M1 will contain the current override value 2 M2 M_NOvrd M2 will contain the initial override value 100 3 M3 M_JOvrd M3 will contain the current joint override value 4 M4 M_NJovrd M4 will contain the initial joint override value 5 M5 M_OPovrd M5 will contain the current OP operation panel override value 6 M6 M_Ovrd ...

Страница 297: ...00 Return the acceleration deceleration time 9 EndIf 10 GoTo 20 Explanation 1 The load ratio of each axis can be referenced 2 The load ratio is derived from the current that flows to each axis motor and its flow time 3 The load ratio rises when the robot is operated with a heavy load in a severe posture for a long period of time 4 When the load ratio reaches 100 an overload error occurs In the abo...

Страница 298: ...d by slot 2 Explanation 1 This can be used to monitor the line being executed by other tasks during multitask operation 2 This variable only reads the data M_Mode Function Returns the key switch mode of the operation panel 1 TEACH 2 AUTO OP 3 AUTO Ext Format Terminology Numeric Variable Specifies the numerical variable to assign Reference Program 1 M1 M_Mode M1 will contain the key switch status E...

Страница 299: ...M_On or 0 M_Off Format Terminology Numeric Variable Specifies the numerical variable to assign Reference Program 1 M1 M_On 1 is assigned to M1 2 M2 M_Off 0 is assigned to M2 Explanation 1 Always returns 1 or 0 2 This variable only reads the data Example Numeric Variable M_On Example Numeric Variable M_Off ...

Страница 300: ...ue differ corresponding to the file type specified by Open command as follows Refer to separate manual Ethernet Interface INSTRUCTION MANUAL when using the ethernet Related instructions Open Open Related parameter COMDEV Example Numerical variable M_Open File number Kind of files Meaning Value File Returns the status indicating whether or not a file is opened Returns 1 until the Close instruction ...

Страница 301: ... 3 M_Outw 2 HFFFF Turns ON 16 bits starting from the output signal 2 4 M4 M_Outb 2 AND H0F M4 will contain the 4 bit information starting from output signal 2 Explanation 1 This is used when writing or referencing external output signals 2 Numbers in 900 s will be used as I O signals for the hand 3 Numbers 6000 and beyond will be referenced assigned to the CC Link optional 4 Refer to Page 193 Dly ...

Страница 302: ...fied task slot 2 This variable only reads the data M_Ratio Function Returns how much the robot has approached the target position 0 to 100 while the robot is moving Format Terminology Numeric Variable Specifies the numerical variable to assign Equation 1 to 32 Specifies the task slot number If this parameter is omitted the current slot will be used as the default Reference Program 1 Mov P1 WthIf M...

Страница 303: ...at a specific position while the robot is moving 2 This variable only reads the data M_Run Function Returns whether the program for the specified task slot is being executed 1 Executing 0 Not executing paused or stopped Format Terminology Numeric Variable Specifies the numerical variable to assign Equation 1 to 32 Specifies the task slot number If this parameter is omitted the current slot will be...

Страница 304: ...urn the acceleration deceleration time distribution rate of the J2 axis to 100 8 Mov P3 Acceleration 100 deceleration 50 9 Accel 100 100 Return the overall deceleration distribution rate to 100 10 Mov P4 Explanation 1 The acceleration deceleration time distribution rate when optimum acceleration deceleration is enabled can be set in units of axes If 100 is specified the acceleration deceleration t...

Страница 305: ...ent slot will be used as the default Reference Program 1 Mov P1 WthIf M_In 10 1 Skip If the input signal 10 is 1 when starting to move to P1 skip the Mov instruction 2 If M_SkipCq 1 Then GoTo 1000 If Skip instruction has been executed jump to line 1000 1000 End Explanation 1 Checks if a Skip instruction has been executed 2 This variable only reads the data 3 If the M_SkipCq variable is referenced ...

Страница 306: ... the directive speed at which the robot is operating 2 This can be used in M_RSpd multitask programs or with Wth and WthIf statements 3 This variable only reads the data M_Svo Function Returns the current status of the servo power supply 1 Servo power ON 0 Servo power OFF Format Terminology Numeric Variable Specifies the numerical variable to assign Mechanism Number Enter the mechanism number 1 to...

Страница 307: ...on Enter the number to 8 from 1 Parentheses are required Reference Program 1 M_Timer 1 0 2 Mov P1 3 Mov P2 4 M1 M_Timer 1 M1 will contain the amount of time required to move from P1 to P2 in ms Example If the time is 5 346 sec the value of M1 is 5346 5 M_Timer 1 Set to 1 5 sec Explanation 1 A value may be assigned The unit is seconds when set to M_Timer 2 Since measurement can be made in milliseco...

Страница 308: ...encing the Tool Number 1 If M_In 900 1 Then Change the tool data by a hand input signal 2 M_Tool 1 Set tool 1 in tool data 3 Else 4 M_Tool 2 Set tool 2 in tool data 5 EndIf 6 Mov P1 Explanation 1 The values set in the MEXTL1 MEXTL2 MEXTL3 and MEXTL4 tool parameters are reflected in the tool data It is also written into the MEXTL parameter 2 Tool numbers 1 to 4 correspond to MEXTL1 to 4 3 While ref...

Страница 309: ...riable Specifies the numerical variable to assign Mechanism Number Enter the mechanism number 1 to 3 If the argument is omitted 1 is set as the default value Reference Program 1 M1 M_Uar 1 M1 indicates whether the robot is within or outside the user defined area The value 4 indicates that the robot is in the user defined area 3 Explanation 1 For details on how to use user defined areas refer to Pa...

Страница 310: ... a negative value results in decimal notation if bit 31 is 1 and therefore it is recommended that hexadecimal notation be used 5 This variable only reads the data Related System Variables M_Uar M_Uar32 and User defined Area Compatibility Example If contained in user defined area 5 and 10 this will be the combined value of H00000010 the value indicating area 5 and H00000400 the value indicating are...

Страница 311: ...iable to assign Equation 1 to 32 Specifies the task slot number If this parameter is omitted the current slot will be used as the default Reference Program 1 M1 M_Wai 1 M1 will contain the standby status of slot 1 Explanation 1 This can be used to check whether the program has been paused 2 Combine M_Run and M_Wai to determine if the program has stopped in case the currently executed line is the t...

Страница 312: ...ng the speed 2 If the warm up operation mode is disabled the MODE switch on the front of the controller is set to TEACH or the machine is being locked the value is always 100 3 If the normal status changes to the warm up operation status or the warm up operation status is set immediately after power on the value specified in the first element the initial value of a warm up oper ation override of t...

Страница 313: ... always returned 3 If the normal status changes to the warm up operation status or the warm up operation status is set immediately after power on the time specified in the first element the valid time of the warm up opera tion mode of the WUPTIME parameter is set as the initial value and the value of M_Wuprt decreases according to the operation of the robot And when the value is set to 0 the warm ...

Страница 314: ...e WUPAXIS parameter warm up operation mode target axis continues to stop operating while the robot s warm up operation status the status in which operation is performed by automatically reducing the speed is canceled 2 If the warm up operation mode is disabled the time specified in the second element warm up operation mode resume time of the WUPTIME parameter is returned 3 If a target axis operate...

Страница 315: ...nter the mechanism number 1 to 3 If the argument is omitted 1 is set as the default value Reference Program 1 P1 P_Base P1 will contain the base conversion data that is currently being set 2 Base P_NBase Resets the base conversion data to the initial value Explanation 1 P_NBase will contain 0 0 0 0 0 0 0 0 2 Be careful when using base conversion since it may affect the teaching data 3 Use the Base...

Страница 316: ... a ratio using the maximum travel axis as 1 0 Example If the robot was being operated at a ratio of X axis direc tion Y axis direction 2 1 P_ColDir 1 0 5 0 0 0 0 0 0 3 The posture axis and structural flag are always 0 0 0 0 0 0 0 4 A value is calculated when an impact is detected and then that value is retained until the next impact is detected 5 If an impact is detected when an external object hi...

Страница 317: ... default value Reference Program 1 Def Act 1 M_In 10 1 GoTo 1000 Defines interrupt 2 Act 1 1 Enables interrupt 3 Mov P1 4 Mov P2 5 Act 1 0 Disables interrupt 100 P100 P_Curr Loads the current position when an interrupt signal is received 101 Mov P100 100 Moves 100 mm above P100 i e 100 mm in the Z direc tion of the tool 102 End Ends the program Explanation 1 This can be used to identify the curren...

Страница 318: ...on the feedback values from the servo 2 This variable only reads the data Reference Torq Torque J_Fbc J_AmpFbc M_Fbd P_Safe Function Returns the safe point XYZ position of the JSAFE parameter Format Terminology Position Variables Specifies the position variable to assign Mechanism Number Enter the mechanism number 1 to 3 If the argument is omitted 1 is set as the default value Reference Program 1 ...

Страница 319: ...ol P1 will contain the tool conversion data Explanation 1 P_Tool returns the tool conversion data set by the Tool instruction or the MEXTL parameter 2 Use the Tool instruction when changing tool data 3 This variable only reads the data P_Zero Function Always returns 0 0 0 0 0 0 0 0 0 0 Format Terminology Position Variables Specifies the position variable to assign Reference Program 1 P1 P_Zero 0 0...

Страница 320: ...n Format This indicates how to input the function argument Reference Program An example program using function is shown Terminology This indicates the meaning and range of an argument Explanation This indicates detailed functions and precautions Reference This indicates related function 4 13 2 Explanation of Each Function Each variable is explained below in alphabetical order ...

Страница 321: ...e of a given value Format Reference Program 1 P2 C Abs P1 C P2 C will contain the value of P1 C without the sign 2 Mov P2 3 M2 100 4 M1 Abs M2 100 is assigned to M1 Explanation 1 Returns the absolute value Value with the positive sign of a given value Reference Sgn Numeric Variable Abs Equation ...

Страница 322: ... the Mov instruction Format Reference Program 1 P1 P_Curr 2 P2 Align P1 3 Mov P2 Explanation 1 Converts the A B and C components of the position data to the closest XYZ postures 0 90 and 180 2 Since the return value is of position data type an error will be generated if the left hand side is of joint variable type 3 This function cannot be used in vertical multi joint 5 axes robot The following sh...

Страница 323: ... 1 M1 Atn 100 100 PI 4 is assigned to M1 2 M2 Atn2 100 100 PI 4 is assigned to M1 Explanation 1 Calculates the arc tangent of a given equation Unit is in radians 2 The range of the returned value for Atn is PI 2 Atn PI 2 3 The range of the returned value for Atn2 is PI Atn PI 4 If Equation 2 evaluates to 0 Atn2 will return PI 2 when Equation 1 evaluates to a positive value and PI 2 when Equation 1...

Страница 324: ... will contain the character string of 11111111 Explanation 1 Value is converted to a binary string 2 If the equation does not evaluate to an integer the integral value obtained by rounding the fraction will be converted to a binary string 3 Val is a command that performs the opposite of this function Reference Hex Str Val Character String Variable Bin Equation ...

Страница 325: ...r occurs 3 MR M10 Radius 4 MRD M20 Circular arc angle 5 MARCLEN M30 Circular arc length 6 PC P10 Coordinates of the center point Explanation 1 Provides information regarding the arc that is determined by the three specified points position 1 posi tion 2 and position 3 2 If the arc generation and calculation of various values succeeded 1 will be returned as the return value 3 If some points have th...

Страница 326: ...teger the character will be returned whose character code cor responds to the integral value obtained by rounding the fraction Reference Asc Cint Function Rounds the fractional part of an equation to convert the value into an integer Format Reference Program 1 M1 Cint 1 5 2 is assigned to M1 2 M2 Cint 1 4 1 is assigned to M2 3 M3 Cint 1 4 1 is assigned to M3 4 M4 Cint 1 5 2 is assigned to M4 Expla...

Страница 327: ...ge of the string an error will be generated 3 If the end position exceeds the end of the string checksum from the starting position to the last character in the string will be calculated 4 If the result of addition exceeds 255 a degenerated value of 255 or less will be returned 5 It is not possible to describe a function that contains an argument in Character String Equation 1 and Equation 2 If su...

Страница 328: ...ount of communication data when transmitting numerical data with external devices Reference Asc Cvs Cvd Mki Mks Mkd Cvs Function Converts the character codes of the first four characters of a string into a single precision real number Format Reference Program 1 M1 Cvs FFFF 12689 6 is assigned to M1 Explanation 1 Converts the character codes of the first four characters of a string into an single p...

Страница 329: ...s Mki Mks Mkd Deg Function Converts the unit of angle measurement from radians rad into degrees deg Format Reference Program 1 P1 P_Curr 2 If Deg P1 C 170 OR Deg P1 C 150 Then NOERR 3 Error 9100 4 NOERR Explanation 1 Converts the radian value of an equation into degree value 2 When the posture angles of the position data are to be displayed using positional constants the unit used for 500 0 600 18...

Страница 330: ...sed for calculation 3 The joint variables cannot be used Trying to use it will result in an error during execution 4 It is not possible to describe a function that contains an argument in position 1 and position 2 If such a function is described an error will be generated during execution Exp Function Calculates exponential functions an equation that uses e as the base Format Reference Program 1 M...

Страница 331: ...ogram 1 M1 Fix 5 5 5 is assigned to M1 Explanation 1 Returns the integral portion of the equation value 2 If the equation evaluates to a positive value the same number as Int will be returned 3 If the equation evaluates to a negative value then for instance Fix 2 3 2 0 will be observed Reference Cint Int Numeric Variable Fix Equation ...

Страница 332: ...P3 positions 3 P10 Inv P10 4 Base P10 Position of P100 will be used as the origin for robot Explanation 1 This can be used to define the base coordinate system 2 This creates a plane from the three coordinates X Y and Z for the three positions to calculate the posi tion of the origin and the inclination of the plane and returns the result as a position variable The X Y and Z coordinates of the pos...

Страница 333: ...forms this procedure in reverse 5 If number of output characters is specified it is not possible to describe a function that contains an argument in Equation If such a function is described an error will be generated during execution NG example C1 Hex Asc a 1 Reference Bin Str Val Int Function Returns the largest integer that does not exceed the value of the equation Format Reference Program 1 M1 ...

Страница 334: ... value is a position data an error will be generated if a joint variable is used in the left hand side JtoP Function Given joint data will be converted into position data Format Reference Program 1 P1 JtoP J1 The position that expresses the J1 joint type position using the XYZ type will be assigned to P1 Explanation 1 Converts the joint data into the position data 2 Position variables cannot be us...

Страница 335: ...a negative value or is longer than the string 3 It is not possible to describe a function that contains an argument in Character String and Equation If such a function is described an error will be generated during execution Reference Mid Right Len Function Returns the length of the string Format Reference Program 1 M1 Len ABCDEFG 7 is assigned to M1 Explanation 1 Returns the length of the argumen...

Страница 336: ...n error will be generated if the equation evaluates to a zero or a negative value Reference Exp Log Log Function Returns the common logarithm Base 10 Format Reference Program 1 M1 Log 2 0 301030 is assigned to M1 Explanation 1 Returns the common logarithm of the value of the equation 2 An error will be generated if the equation evaluates to a zero or a negative value Reference Exp Ln Numeric Varia...

Страница 337: ...on of the string Format Reference Program 1 C1 Mid ABCDEFG 3 2 CD is assigned to C1 Explanation 1 A string of the length specified by argument 3 is extracted from the string specified by the first argument starting from the position specified by argument 2 and returned 2 An error will be generated if equation 2 or 3 evaluates to a zero or a negative value 3 An error is generated if the position of...

Страница 338: ...n Equation 1 Equation 2 and If such a function is described an error will be generated during execution Reference Max Mirror Function Inverts the bit string representing each character code of the string in binary and obtains the character coded string Format Reference Program 1 C1 Mirror BJ RB is assigned to C1 BJ H42 H4A B01000010 B01001010 Inverted H52 H42 B01010010 B01000010 Output RB Explanat...

Страница 339: ...smitting numerical data to external devices Reference Asc Cvi Cvs Cvd Mks Mkd Mks Function Converts the value of an equation single precision real number into a four byte string Format Reference Program 1 C1 Mks 100 1 2 M1 Cvs C1 100 1 is assigned to M1 Explanation 1 Converts the lowest four bytes of the value of an equation single precision real number into the strings 2 Use Cvs to convert the st...

Страница 340: ...ansmitting numerical data to external devices Reference Asc Cvi Cvs Cvd Mki Mki PosCq Function Checks whether the given position is within the movement range Format Reference Program 1 M1 PosCq P1 M1 will contain 1 if the position P1 is within the movement range Explanation 1 Check whether the position data given by an argument is within the movement range of the robot Value 1 will be returned if ...

Страница 341: ...ied interpolation type For instance an error will be generated if the structure flags of the starting and end points are different 5 It is not possible to describe a function that contains an argument in Position Variables 1 Position Variables 2 Equation 1 and Equation 2 If such a function is described an error will be generated during execution PtoJ Function Converts the given position data into ...

Страница 342: ... Terminology Position Variables Specifies the position variable from which the structure flag will be extracted Equation Specifies which structure flag is to be extracted 0 R L 1 A B 2 N F Reference Program 1 P1 100 0 100 180 0 180 7 0 Since the structure flag 7 B111 is RAN 2 C1 Rdfl1 P1 1 C1 will contain A Explanation 1 Of the structure flags in the position data specified by argument 1 the flag ...

Страница 343: ...is function extracts information from the FL2 element of position data 4 Structure flag 2 multiple rotation information has a 32 bit structure which contains 4 bits of information per axis for 8 axes 5 When displaying in T B and the multiple rotation is a negative value value of 1 to 8 is converted into F to 8 4 bit signed hexadecimal notation and displayed 6 It is not possible to describe a funct...

Страница 344: ...he argument and extracts a random number 2 If the equation provided as the argument evaluates to 0 initialization of random numbers will not take place and the next random number will be extracted 3 When the same value is used to perform initialization of random numbers identical random number sequence will be obtained Right Function Obtains a string of the specified length starting from the right...

Страница 345: ...on data The content of the position data given by the argument will remain unchanged 3 The structure flag will be specified starting from the last character in the string Therefore for instance if the string LR is specified the resulting structure flag will be L 4 If the flags are changed using a numerical value set P1 FL1 7 5 Structure flags may have different meanings depending on the robot mode...

Страница 346: ...changing the position data s multiple rotation information of the joint axis specified by equation 1 to the value specified by equation 2 2 This function changes information from the FL2 element of position data 3 The content of the position of position variables given by the argument X Y Z A B C and FL1 will remain unchanged 4 It is not possible to describe a function that contains an argument in...

Страница 347: ... is used for the J4 and succeeding axes 5 Mov J2 6 Next M1 7 M0 Rad 0 8 M90 Rad 90 7 J3 SetJnt M0 M0 M90 M0 M90 M0 10 Mov J3 Explanation 1 The value of each axis in joint variables can be changed 2 Variable can be described as arguments 3 Arguments can be omitted except for the J1 axis They can be omitted for all subsequent axes Argu ments such as SetJnt 10 10 10 cannot be described 4 In an argume...

Страница 348: ... Only for the value of the Z axis it is rotated by 10 mm each time The same value is used for the A and succeeding axes 5 Mov J2 6 Next M1 Explanation 1 The value of each axis in joint variables can be changed 2 Variable can be described as arguments 3 Arguments can be omitted except for the X axis They can be omitted for all subsequent axes Argu ments such as SetPos 10 10 10 cannot be described 4...

Страница 349: ...alue 1 0 0 Negative value 1 Sin Function Calculates the sine Format Reference Program 1 M1 Sin Rad 60 0 866025 is assigned to M1 Explanation 1 Calculates the sine to which the given equation evaluates 2 The range of values will be the entire range that numerical values can take 3 The range of the return value will be from 1 to 1 4 The unit of arguments is in radians Reference Cos Tan Atn Atn2 Nume...

Страница 350: ...pos ABCDEFG DEF 4 is assigned to M1 Explanation 1 Returns the position of the first occurrence of the string specified by argument 2 from the string specified by argument 1 2 An error will be generated if the length of the argument 2 is 0 3 For instance if argument 1 is ABCDEFG and argument 2 is DEF 4 will be returned 4 If the search string could not be found 0 will be returned 5 It is not possibl...

Страница 351: ... reverse Reference Bin Hex Val Tan Function Calculates the tangent Format Reference Program 1 M1 Tan Rad 60 1 732051 is assigned to M1 Explanation 1 Returns the tangent of the value to which the equation evaluates 2 The range of arguments will be the entire range of values that are allowed 3 The range of return values will be the entire range that numerical values can take 4 The unit of arguments ...

Страница 352: ...ogram 1 M1 Val 15 2 M2 Val B1111 3 M3 Val HF Explanation 1 Converts the given character string expression string into a numerical value 2 Binary B decimal and hexadecimal H notations can be used for the string 3 In the example above M1 M2 and M3 evaluate to the same value 15 Reference Bin Hex Str Numeric Variable Val Character String Expression ...

Страница 353: ... and C they are checked by rotating in the positive direction from the angle in position 2 to position 3 and by seeing if the target value is inside the swiped range Example If P2 A is 100 and P3 A is 100 if P1 A is 50 the value is within the range Similar checking will be performed for B and C axes Refer to diagram below 4 For components that are not checked or do not exist if the unit is in degr...

Страница 354: ...lanation 1 This will check if position 1 is inside the cylindrical area Refer to diagram below defined by the two points position 2 and position 3 and the radius represented by the equation If the point is inside the space 1 is returned otherwise 0 is returned 2 This function checks whether the check position X Y and Z coordinates is within the specified area but does not take the posture componen...

Страница 355: ...ined by the three points position 2 position 3 and position 3 and the Equation W Equation H and Equation L If the point is inside the space 1 is returned otherwise 0 is returned 2 This function checks whether the check position X Y and Z coordinates is within the specified area but does not take the posture components into consideration 3 It is not possible to describe a function that contains an ...

Страница 356: ...Real value 16 Set the overrun limit value for the joint coordinate system Sets the movement range for each axis Expanding of the move ment range is not recommended since there is possibility that the robot may strike the mechanical stopper Set the minus and plus directions J1 J1 J2 J2 J8 J8 Unit deg Setting value for each mechanism XYZ movement range MEPAR Real value 6 Set the overrun limit value ...

Страница 357: ...s the user definition area Invalid In zone signal output Error output 0 1 2 Invalid This function will be invalid In zone signal output The dedicated output signal USRAREA will turn ON Error output An error is generated Posture data will be ignored 0 Invalid USRAREA Defines the number of the signal that outputs the status Refer to Page 416 6 3 Dedicated input output 1 1 Free plane limit Refer to 5...

Страница 358: ...override Operates at OP override x maximum override Operation exceeding the maximum speed 250 mm s cannot be performed Setting value for each mechanism Jog speed limit value JOGSPMX Real value 1 Limit the robot movement speed during the teach mode Unit mm s Even if a value larger than 250 is set the maximum value will be limited to 250 250 0 Automatic return setting after jog feed at pause Refer t...

Страница 359: ...Integer 8 Set the pneumatic hand I F output for when the power is turned ON This parameter specifies the initial value when turning ON the power to the dedicated hand signals 900 S at the robot s tip To set the initial status at power ON when controlling the hand using general purpose I Os other than 900 S or CC Link 6000 S specifying a signal other than one in 900 S by the HANDTYPE parameter do n...

Страница 360: ...r type are secret HNDDAT is 1 to 8 Real value 7 Set the initial condition of the hand Designate with the tool coordi nate system Weight size X size Y Size Z center of gravity X center of gravity Y center of gravity Z Unit Kg mm Standard load 0 0 0 0 0 0 0 0 0 0 0 0 WRKDAT0 Real value 7 Set the work conditions Designate with the tool coordinate sys tem Immediately after power ON this setting value ...

Страница 361: ... COL Integer 3 Define whether the impact detection function can cannot be used and whether it is enabled disabled immediately after power ON Element 1 The impact detection function can 1 cannot 0 be used Element 2 Enable 1 disable 0 as the initial state at automatic operation Element 3 Enable 1 disable 0 NOERR mode 2 during jog operation The NOERR mode does not issue an error even if impact is det...

Страница 362: ...Warm up operation mode 0 Invalid 1 Valid Note If a value other than the above is set everything will be disabled Note For multiple mechanisms this mode is set for each mechanism 0 Invalid Warm up operation mode target axis WUPAXIS Integer 1 Specify the joint axis that will be the target of control in the warm up operation mode by selecting bit ON or OFF in hexadecimal J1 J2 from the lower bits Bit...

Страница 363: ...tional setting of compliance error CMPERR Integer 1 Setting this parameter prevents errors 2710 through 2740 errors that occur if the position command generated in compliance control is abnormal from occurring 1 Enable error generation 0 Disable error generation The contents of applicable errors are as follows 2710 The displacement from the original position command is too large 2720 Exceeded the ...

Страница 364: ... shipped from the factory this setting is set so that it will open at any error level For example if the warning level is ignored and either or both a low level or high level error occurs set 3 to open this output terminal Refer to the following manual for details on the EMGOUT connector Instruction Manual Refer to External Emergency Stop Connection for ROBOT ARM SETUP MAINTENANCE 7 Open for any e...

Страница 365: ...ommunication area setting CRnQ 700 only QMLTCPUn n 1 4 Integer 4 At the multi CPU system set the number of points performing transmission and receipt between each CPU unit for the high speed communication function between multi CPU nos 1 to 4 It is necessary to match the parameter settings for all CPUs An error will occur at the sequencer CPU If the parameter settings do not match and therefore ca...

Страница 366: ...o 1 the offset will be automatically fixed based on the installed slot Compatible with previous versions N4a and prior B By setting to 0 to 14 the input offset is set based on the value Refer to cases A and B in 5 2 1About multi CPU input offsets CRnQ 700 controller only on the following pages Please note that by connecting multiple robots and setting this parameter to the same value anything othe...

Страница 367: ... Robot input Not used Robot CPU No 1 Robot CPU No 2 Robot CPU No 3 Robot I O no bit units Robot I O no bit units Robot I O no bit units 10000 18191 10000 18191 10000 18191 Shared memory word units U3E0 G10000 U3E0 G10511 U3E0 G10512 U3E0 G11023 U3E0 G11024 U3E0 G11535 10000 18191 U3E1 G10000 U3E1 G10511 10000 18191 U3E2 G10000 U3E2 G10511 10000 18191 U3E3 G10000 U3E3 G10511 Sequencer Sequencer out...

Страница 368: ...2 G10000 U3E2 G10511 10000 18191 U3E3 G10000 U3E3 G10511 10000 18191 U3E0 G10000 1 U3E0 G10511 1 10000 18191 U3E0 G10000 2 U3E0 G10511 2 10000 18191 U3E0 G10000 3 U3E0 G10511 3 Shared memory word units Shared memory word units Shared memory word units Shared memory word units Shared memory word units Shared memory word units Sequencer Sequencer Sequencer Sequencer Sequencer Sequencer Sequencer out...

Страница 369: ...on rights when the key switch of the operation panel is in AUTO OP mode External OP 0 1 1 OP RMTPSL Integer 1 Designate the program selection operation rights for the automatic Ext mode External OP 0 1 0 External TB override operation rights OVRDTB Integer 1 Specifies whether the operation rights are required when changing override from T B Not required Required 0 1 1 Required Speed setting during...

Страница 370: ...aintenance Forecast Note When reading this parameter form the teaching pendant enter all parameter names and then read MFGRST Integer 1 Reset the accumulated data relating to grease in the maintenance forecast function When axes generated a warning numbered in 7530 s that prompts the replenishment of grease in the maintenance forecast function and as a result grease was replenished the data relati...

Страница 371: ... 0 0 0 0 0 0 0 0 MEXDTL2 Real value 6 The correction data for tool number 2 obtained by the Position Restoration Support tool is input Do not change it with any tool other than the Position Restoration Support tool X Y Z A B C 0 0 0 0 0 0 0 0 0 0 0 0 MEXDTL3 Real value 6 The correction data for tool number 3 obtained by the Position Restoration Support tool is input Do not change it with any tool ...

Страница 372: ...This is executed by the START button on the operation panel or by the start signal ALWAYS This is executed immediately after the controller s power is turned on This program does not affect the status such as startup To edit a program whose attribute is set to ALWAYS first cancel the ALWAYS attribute A program with the ALWAYS attribute is being executed con tinuously and therefore cannot be edited...

Страница 373: ...atus of program selection is not maintained at the end of cycle operation The parameter value becomes P 0000 Setting values and operations 0 Disable storage do not maintain 1 Enable storage do not maintain initial value 2 Disable storage maintain 3 Enable storage maintain 1 Valid Setting that allows the execution of X instructions and Servo instruc tion in an ALWAYS pro gram Refer to 5 11Automatic...

Страница 374: ...e amount to increment or decrement with the JRC com mand in the order of J1 J2 J3 to J8 axes from the head element The setting is valid only for the user defined axis so the J7 and J8 axes will be valid for the robot s additional axis and a random axis for the mechanism s additional axis The unit relies on the parameter AXUNT JRC execution valid robot 0 0 0 0 0 360 0 0 or 0 0 0 360 0 0 0 0 JRC exe...

Страница 375: ... specifi cation Extension of external vari able PRGGBL Sets 1 to this parameter and turns on the controller power again then the capacity of each program external variable will double However if a variable with the same name is being used as a user defined external variable an error will occur when the power is turned ON and it is not possible to expand It is necessary to correct the user definiti...

Страница 376: ...cifies the device that corresponds to COMn speci fied in the Open statement in the program n is between 1 and 8 Parameters are starting from the left COM1 COM2 COM8 in that order Note Since the communication interface is not prepared for robot CPU of the notes CRnQ 700 series and the drive unit this parameter cannot be used RS232 CBAU232 Integer 1 Baud rate 9600 19200 9600 CPRTY232 Integer 1 Parit...

Страница 377: ...s rotation in the tool coordinate system C axis Z axis rotation in the tool coordinate system A case for a vertical 6 axis robot 1 Sample parameter setting Parameter name MEXTL Value 0 0 95 0 0 0 2 Sample Tool instruction setting 1 Tool 0 0 95 0 0 0 A 6 axis robot can take various postures within the movement range A case for a vertical 5 axis robot 1 Sample parameter setting Parameter name MEXTL ...

Страница 378: ...valid depending on the robot model See Table 5 8 to set the appropriate data Table 5 8 Valid axis elements of the tool conversion data depending on the robot model Type Number of axis An axis element of the tool conversion data Note1 Note1 O Valid X Invalid This is meaningless and ignored if set X The setting value is fixed to 0 If a value other than 0 is set operation may be adversely affected X ...

Страница 379: ... C axis Z axis rotation in the base coordinate system Example 1 Sample parameter setting Parameter name MEXBS ValueÅF100 150 0 0 0 30 2 Sample Base instruction setting 1 Base 100 150 0 0 0 30 Normally the base coordinate system need not be changed If you wish to change it see the sample above when configuring the system Note that the Base instruction within the robot pro gram may shift the robot t...

Страница 380: ...tal multi joint type robots make sure that AREA P1 is set to 360 and AREA P2 is set to 360 4 AREA ME specifies to which mechanism will the area checking configuration apply Under the standard configuration one unit is connected this is set to 1 5 AREA AT specifies the type of area checking The meaning of the value is shown below 0 Does not check 1 Outputs a signal 2 Generates an error If 2 posture...

Страница 381: ... the 3 points that define the plane P1 coordinates X1 Y1 and Z1 The origin of the plane P2 coordinates X2 Y2 Z2 A position on the X axis of the plane P3 coordinates X3 Y3 Z3 A position in the positive Y direction of the X Y plane in the plane SFCnME n 1 to 3 Specifies the mechanism number to which the free plane limit applies Usually set up 1 In the case of multiple mechanisms the mechanism number...

Страница 382: ...ition In this case adjust the position of the robot to the sus pended position and resume moving the robot If RETPATH 1 or 2 is set as shown in the figure below and the robot is operated continuously continuous path operation using the Cnt instruction the robot returns to a position on the travel path from P1 to P2 instead of the suspended position When RETPATH 0 is set the robot moves to the targ...

Страница 383: ...c return setting after jog feed at pause 5 370 P1 P2 P1 P2 RETPATH 1 or 2 RETPATH 0 Move to target position Jog feed Interrupt here Resume the automatic execution Jog feed Move to target position Resume the automatic execution Interrupt here ...

Страница 384: ...ame start condition and operation status The point here is the start condition ALWENA 0 7 In the ALWAYS program it is possible to execute multitask related instructions such as XRun and XLoad and also the Servo instruction 1 Auto Start Sample Program 2 3 Execute Program 1 if the key switch is AUTO Ext 4 Stop the program and return the execution line to the beginning of the program if the key switc...

Страница 385: ...rs 1 through 4 or 8 will be used as the argument in the hand open close instructions HOpen or HClose Setting method When a double solenoid type is used D must be added in front of the signal number to specify the number In the case of double solenoid type hand number will be from 1 to 4 When a single solenoid type is used S must be added in front of the signal number to specify the number In the c...

Страница 386: ...he workpiece may be dropped when the power is turned ON Caution2 This parameter specifies the initial value when turning ON the power to the dedicated hand sig nals 900 s at the robot s tip To set the initial status at power ON when controlling the hand using general purpose I Os other than 900 s or CC Link 6000 s specifying a signal other than one in 900Åfs by the HANDTYPE parameter do not use th...

Страница 387: ...000 ORST224 00000000 00000000 00000000 00000000 PROFIBUS option ORST2000 00000000 00000000 00000000 00000000 ORST2032 00000000 00000000 00000000 00000000 ORST2064 00000000 00000000 00000000 00000000 ORST2096 00000000 00000000 00000000 00000000 ORST2128 00000000 00000000 00000000 00000000 ORST2160 00000000 00000000 00000000 00000000 ORST2192 00000000 00000000 00000000 00000000 ORST2224 00000000 000...

Страница 388: ...ror is generated next time the power is turned on Sequencer link Note1 ORST10000 信号番号 10000 10007 10008 10015 10016 10023 10024 10031 00000000 00000000 00000000 00000000 ORST10032 10032 10039 10040 10047 10048 10055 10056 10063 00000000 00000000 00000000 00000000 ORST10064 00000000 00000000 00000000 00000000 ORST10096 00000000 00000000 00000000 00000000 ORST10128 ORST18160 00000000 00000000 000000...

Страница 389: ...l equipment Carry out communication by the commands Open Close Print Input etc of the communication relation on the robot program Call this the data link The controller cannot be controlled from external devices such as a PC i e automatic execution or status monitoring If this is necessary contact the dealer or branch from where the robot has been purchased for further consultation Machine cable M...

Страница 390: ... Set to grasping Depending on the hand s open close status optimum acceleration deceleration calculation will be per formed for either hand alone condition or hand and workpiece condition The hand s open close status can be changed by executing the HOpen HClose instruction The coordinate axes used as references when setting the hand and workpiece conditions are shown below for each robot model The...

Страница 391: ... elements of the center of gravity and the X Y and Z elements of the size must be set Y X 6 axis type Z X Y Definitions of Coordinate Axes In the coordinate system with the tip of the J4 axis as the origin Z axis The upward direction is positive X axis The direction of extension in the arm orientation is positive Y axis A right hand coordinate system Axes that must be set Only the X element of the...

Страница 392: ...eturn operations 3 MS position moving operation 4 Direct execution operation If the robot approaches a singular point by any of the operations listed above the buzzer of the controller keeps buzzing continuous sound However the STATUS NUMBER display on the operation panel does not change Also in the case of 1 Jog operation other than joint jog mode above a warning is displayed on the T B screen to...

Страница 393: ...ting and renaming the programs in the controller by using the T B and personal computer support software Parameter Description and value ROMDRV Switches the access target of the programs between ROM and RAM 0 RAM mode initial value 1 ROM mode 2 High speed RAM mode high speed RAM operation DRAM memory is used BACKUP Copies programs parameters common variables and error logs from the RAM area into t...

Страница 394: ...ter ROMDRV Power ON ROM mode 1 RAM mode 0 high speed RAM mode 2 File System ROM Area SRAM Area Exection Area DRAM Aerea high speed Execution SRAM Area Save enabled Target of executable programs Programs to be backed up Changing parameters Saving error logs Reading programs Editing writing programs Copying moving and renaming programs Files to be access by the OPEN instruction Program Exection Area...

Страница 395: ...ams may be read during the ROM operation but they cannot be written Similarly programs can nei ther be copied nor renamed About parameters Parameters and error log files are always saved in the RAM area regardless of switching between the ROM operation and the RAM operation However the RLNG parameter for switching the robot language refer to Page 362 RLNG cannot be changed during the ROM operation...

Страница 396: ...he following shows the procedures for switching ROM operation RAM operation and high speed RAM operation For more information about the operating procedure of each of the above see the following pages P o w e r O N E n t e r B A C K U P p a r a m e t e r C a n c e l C a n c e l p a r a m e t e r P o w e r O F F t o O N C h a n g e R O M D R V p a r a m e t e r f r o m 0 t o 1 P o w e r O F F t o O...

Страница 397: ...rogram check is complete the cursor moves to the parameter name field If any abnormality is found during the program check an error is output and the date of ROM write operation is registered in an error log Cancel Operation When the function key corresponding to the CLOSE is pressed then data is not changed 4 Be sure to shut off the power here Also be sure to shut off the power during Cancel Oper...

Страница 398: ...described above START STATUS NUMBER STATUS NUMBER STATUS NUMBER STATUS NUMBER STATUS NUMBER STATUS NUMBER Power ON Approx 8 sec Approx 12 sec Approx 22 sec STATUS NUMBER Power ON The completion of writing into the ROM area is displayed This display varies depending on whether or not there is extension memory OK0 W hen standard memory is used OK3 W hen 2 MB extension memory is used W hen 2 MB exten...

Страница 399: ...on is performed an error will occur To edit a program cancel the ROM operation change the value of the ROMDRV parameter from 1 to 0 and reset the power to the controller first and then edit it To switch back to the ROM operation after the completion of program editing be sure to perform the operation Copy Pro grams to ROM Area STATUS NUMBER STATUS NUMBER STATUS NUMBER STATUS NUMBER STATUS NUMBER S...

Страница 400: ...e data field press the EXE key again The cursor moves to the parameter name field 5 Be sure to shut off the power here Also be sure to shut off the power during Cancel Operation in step 3 above Copy to the RAM area is performed the next time the power is turned on If the power is not shut off after the operation in step 3 data will not be properly copied into the RAM area 6 Turn on the power to th...

Страница 401: ... Power ON The completion of restoring into the RAM area is displayed This display varies depending on whether or not there is extension memory OK4 W hen standard memory is used OK7 W hen 2 MB extension memory is used The time required to start up after the power is turned on is almost the same as the normal operation which is different from when writing to the ROM area Approx 12 sec Press the STAR...

Страница 402: ...value of the ROMDRV parameter from 0 to 2 After changing it be sure to shut off the power and turn it on again 2 Change back the parameter and return to RAM operation Change the value of the ROMDRV parameter from 2 to 0 After changing it be sure to shut off the power and turn it on again PARAMETER NAME ROMDRV ELE DATA 0 CLOSE 123 Next DATA Prev PARAMETER NAME ROMDRV ELE DATA 2 CLOSE 123 Next DATA ...

Страница 403: ... in the WUPENA parameter and power on the con troller again Note To use the warm up operation mode on the robot other than the RV SD series it is necessary to spec ify a joint axis to be the target of the warm up operation mode in the WUPAXIS parameter other than the WUPENA parameter For more information see 2 Function Details When the Warm Up Operation Mode Is Enabled When the warm up operation m...

Страница 404: ... status is canceled the robot operates at the speci fied speed Note that the joint section cools down at a low temperature if the robot continues to stop after the warm up operation status is canceled Therefore if a target axis continues to stop for a prolonged period the setting value at shipment from the factory is 60 min the warm up operation status is set again and the robot operates at a redu...

Страница 405: ...anceled if a target axis continues to stop Setting range 1 to 1440 WUPOvrd Perform settings pertaining to the speed in the warm up operation status Specify the initial value in the first element and the value constant time in the second element The unit is for both Initial value Specify the initial value of an override warm up operation override to be applied to the operation speed when in the war...

Страница 406: ...input signal above to function it is necessary to enable the warm up oper ation mode in advance by setting the parameters described previously Note 2 This dedicated input signal requires the operation right of external I O Also no input is accepted during operation or jog operation Note 3 The enable disable status specified by this dedicated input signal is held even after the control right of ext...

Страница 407: ...e warm up operation status is exceeded the normal status switches to the warm up operation status again Canceling the warm up operation status If the accumulated time a target axis has operated exceeds the valid time of the warm up operation status the warm up operation status is canceled and the normal status is set Specify the valid time of the warm up operation status in the first element of th...

Страница 408: ...initial value is 70 and the ratio is 50 30 sec in the settings at shipment from the factory These values can be checked with the M_Wupov status variable Fig 5 7 Changes in Warm Up Operation Override Normal status Operating Stopping Accumulated value of target axis operation time Time during which a target axis continues to stop Warm up operation status Valid time Resume time Because the accumulate...

Страница 409: ...perating in the warm up operation status If an error occurs when the warm up operation override is set to the initial value decrease the value of the initial value the first element of the WUPOvrd parameter If an error occurs while the warm up operation override is increasing to 100 the valid time of the warm up operation status or the value constant time may be too short Increase the value of the...

Страница 410: ...ositions are called singular points and they cannot be reached through XYZ jog and linear interpolation based operation To avoid this prob lem in the past the operation layout had to be designed such that no singular points would exist in the work ing area or the robot had to be operated using joint interpolation if it could not avoid passing a singular point The singular point passage function al...

Страница 411: ...ion The robot can pass a singular point when the robot s motion path passes through the singular point If the motion path does not go through the singular point passes near the singular point the robot continues operation without switching the value of the structure flag Positions D E F The robot s motion path passes through a singular point the structure flag switches before and after position E ...

Страница 412: ...in the past is performed the models supporting the singular point passage function are the RV 3SD 3SDJ 6SD 6SDL 12SD 12SDL 18SD series 2 It is not possible to specify multiple axes to perform jog operation at the same time when passing a sin gular point If it is attempted to operate an axis while another axis is operating the operation is ignored 3 A singular point adjacent alarm is generated if t...

Страница 413: ... is set as the upper limit and the robot automatically lowers the speed down to the level where a speed error does not occur near a singular point 4 The optimal acceleration deceleration is not applied for interpolation instructions for which the singular point passage function is specified the robot operates with a fixed acceleration deceleration At this point if the acceleration time and the dec...

Страница 414: ...sage function may affect the execution speed of programs as the function involves complicated processing Specify the singular point passage function only for interpolation instructions where the function is required NonFlip Singular point The structure flag changes from NonFlip to Flip as the robot passes a singular point NonFlip Singular point The structure flag remains NonFlip as the robot does ...

Страница 415: ...tection function is enabled or disabled Even if the impact detection function is enabled it is not possible to prevent dam age to robots hands and workpieces due to interference with peripheral devices completely As a general rule pay sufficient attention to avoid interference with peripheral devices when operating and handling robots Interference detection principle If a robot interferes with per...

Страница 416: ...gram operation This value is a scaling factor that amplifies the detection level standard value prescribed in the impact detection function The smaller the value the higher the detection level Setting range 1 to 500 unit The setting varies depending on the model COLLVLJG Set the detection level sensitivity of each joint axis at jog operation including pause status This value is a scaling factor th...

Страница 417: ...e 2 is specified for element 3 of the COL parameter no error is generated but the robot stops as the servo is turned off an error numbered in the 1010 s will be recorded in the error history however Operation after interference If the servo is turned on while a hand or arm is in contact with peripheral devices or similar the impact is detected again which may prevent the servo from being turned on...

Страница 418: ... the workpiece conditions via tool coordinates 0 0 0 0 0 0 0 0 0 0 0 0 0 0 HNDHOLD is 1 to 8 Specify whether to grab 1 or not grab 0 workpieces when the HOpen and HClose instructions are executed 0 1 Instruction Status variable Description ColChk Enables or disables the impact detection function or specifies the NOERR mode Example ColChk ON Enable the impact detection function COLLVL Specifies the...

Страница 419: ...alue may fluctu ate repeat the target operation several times and record the J_ColMxl value each time 4 Obtain the maximum value for each joint axis from multiple J_ColMxl values and add some margin e g 20 to the value Then set this value as the argument of the COLLVL instruction 5 Set the value obtained in step 4 to the COLLVL instruction and run the program to check that no erroneous detection o...

Страница 420: ...ration The set tings for these operations are thus made independently in order to optimize the impact detection function for each type of operation Here the terms at jog operation and at program operation refer to the following At jog operation During jog operation or during pause of automatic operation At program operation During automatic operation during step feed return operation or during pos...

Страница 421: ...ning signals from peripheral equipment and when checking the robot position 3 Hand input output These are control signals for the hand and are used for reading hand open and close instructions and information from sensors attached to the hand These signals can be controlled at the user program and are wired up to near the tip of the hand Hand output signals are optional Table 6 1 Overall I O signa...

Страница 422: ...nit is equipped 2 Synchronous start up between multi CPUs It takes the robot CPU system several seconds to start up from the time the power is turned ON It is therefore recommended that synchronous start up be set check box selected at the multi CPU system 3 High speed communication area between multi CPUs setting Set the number of points in K word units The robot CPU uses only 1K word or less and...

Страница 423: ...be set to 0 Third element System area size K points Range 1 or 2 Fourth element Multi CPU synchronous start up 1 Yes 2 No Robot CPUs take some time to start up and therefore the current setting of 1 synchronous start up should not be changed Make the same settings for all CPUs 1 0 1 1 Parameter name Details Factory setting Table 6 3 Setting range by number of CPU CPU quantity Setting range 2 0 to ...

Страница 424: ...the U3E0 G10000 and U3E0 G10001 shared device memory and this represents the input from the sequencer to the robot The U3E1 G10000 and U3E1 G10001 shared device memory is read to the bit devices for M200 to M231 and this represents the output from the robot to the sequencer 17 to 22nd row By turning X0 ON M105 turns ON and the sequencer U3E0 G10000 bit 5 corresponding to M105 turn ON Consequently ...

Страница 425: ...1 Sequence ladder example Stop input Robot numerical value input Under the waiting Robot numerical value output Operation rights input Operation rights is robot Opera tion rights button robot Complete of control ler power ON Complete of control ler power ON Operation rights ...

Страница 426: ...N input signal In servo ON output signal 10010 10010 SRVOFF Servo OFF input signal Servo ON disable output signal 10011 10011 CYCLE Cycle stop input signal In cycle stop operation output signal 10012 10012 SAFEPOS Safe point return input signal In safe point return output signal 10013 10013 BATERR Battery voltage drop 10014 OUTRESET General purpose output signal reset 10015 HLVLERR High level erro...

Страница 427: ...utput signal state 901 10049 Hand output signal state 902 10050 Hand output signal state 903 10051 Hand output signal state 904 10052 Hand output signal state 905 10053 Hand output signal state 906 10054 Hand output signal state 907 10055 HNDSTS1 Hand input signal state 900 10056 Hand input signal state 901 10057 Hand input signal state 902 10058 Hand input signal state 903 10059 Hand input signal...

Страница 428: ...y previous series is shown in Table 6 6 Table 6 6 Comparison of the I O point Item CRnQ700 series CRn500 series Sequencer link Remote I O CC Link option PROFIBUS option I O point Bit 8192 8192 256 256 126 126 max 3082 3082 max At four station occupancy The number sum total of I O data 192 words the input or output data number is 122 words max Register 0 0 0 0 16 16 max At four station occupancy 0 ...

Страница 429: ...ng 10003 1 No meaning 1 Output Teaching mode output This output indicates that the key switch on the operation panel is set to Teaching mode ATTOPMD Input 1 No meaning 10004 1 No meaning 1 Output Automatic mode output This output indicates that the key switch on the operation panel is set to AUTO OP IOENA Input Operation rights input signal Sets the validity of the operation rights for the externa...

Страница 430: ...gram reset This input cancels the paused status of the program and brings the executing line to the top Executing a program reset makes it possi ble to select a program In the multitask mode the program reset is applied to all task slots However slots whose starting condition is set to ALWAYS or Error via a parameter SLT will not be executed Edge 10008 10008 1 1 Output Program selection enabled ou...

Страница 431: ...bot will not move and pro gram operation will be enabled SAFEPOS Operation right required Input Safe point return input signal Requests the safe point return operation This signal initiates a joint interpolation move ment to the position set by the parameter JSAFE The speed is determined by the override setting Be careful not to interfere with peripheral devices Edge 10013 10013 1 1 Output In safe...

Страница 432: ...ing the start of output to the numerical input IODATA This signal should also be output to the robot for at least 30 ms Edge 10020 1 Output OVRDSEL Operation right required Input Override selection input signal Designates the setting value for the override with the numeric value input signals Output this signal when at least 30 ms has elapsed following the start of output to the numerical input IO...

Страница 433: ...e error number output in progress status is output to the numerical output JOGENA Operation right required Input Jog valid input signal Jogs the designated axis in the designated mode Operation takes place while this signal is ON Level 1 1 1 1 Output Jog valid output signal Outputs that the jog operation is entered JOGM Input Jog mode input start No end No Designates the jog mode 0 1 2 3 4 Joint X...

Страница 434: ...evel error error number 31 will be generated Level 1 1 1 1 Output Mechanism n pneu matic error output signal Outputs that a pneumatic pressure error is occurring USRAREA Refer to Page 367 5 8 About user defined area Input Note5 10064 Start bit 10071 End bit Note5 1 Start bit 1 End bit Output User designated area 8 points start No end No Outputs that the robot is in the user designated area The out...

Страница 435: ... 10027 10030 10027 10031 Note 3 Set in the order of input start No input end No output start No and output end No When using as the actual jog mode use from the start No to the end No and express as a binary The start No indicates the low order bit and the end No indicates the high order bit Set only the numbers required to express the value For example when using only the joint mode and XYZ mode ...

Страница 436: ...m n warm up operation mode enable input START SnSTART n 1 to 32 Start input These function only when the external input output has the operation rights when IOENA output is ON SLOTINIT Program reset SRVON MnSRVON n 1 to 3 Servo ON input MELOCK MnMELOCK n 1 to 3 Machine lock input SAFEPOS Safe point return input PRGSEL Program selection input OvrdSEL Override selection input JOGENA Jog enable input...

Страница 437: ...ls Remote mode output ATEXTMD Indicates when the key switch on the operation panel is Auto Ext Output Teach mode output TEACHMD Indicates when the key switch on the operation panel is TEACH Output Auto mode output ATTOPMD Indicates when the key switch on the operation panel is Auto Op Output Operation right input IOENA Operation right output IOENA Intput Output Level When the STOP signal or the em...

Страница 438: ...ART or SnSTART signal was input Program reset SLOTINIT Program selectable output SLOTINIT Intput Output 30 ms or more Error reset input ERRRESET Output during error occurrence ERRRESET Intput Output When the SRVOFF SnSRVOFF or emergency stop signal was input Servo ON input SRVON Output during servo ON SRVON Intput Output 30 ms or more Servo OFF input SRVOFF Servo ON disable output SRVOFF Intput Ou...

Страница 439: ...ut Output When returning to retreat point is complete Return to retreat point input SAFEPOS Output during return to retreat point SAFEPOS Intput Output 30 ms or more Output Low battery voltage BATERR Indicates that the battery voltage is low Intput General purpose output signal reset OUTRESET Resets the general purpose output signal 30 ms or more Output High level error output HLVLERR Indicates th...

Страница 440: ...SnSTOP Output during slot n aborting SnSTOP Intput Output 30 ms or more When the SRVON SnSRVON or SRVON signal was input Mechanical n servo OFF input MnSRVOFF Mechanical n servo ON disable output MnSRVOFF Intput Output 30 ms or more When the SRVOFF SnSRVOFF or emergency stop signal was input Mechanical n servo ON input MnSRVON Output during mechanical n servo ON MnSRVON Intput Output 30 ms or more...

Страница 441: ...e When the output request of a program number line number or error number was input Override value output request OVRDOUT Override value output request OVRDOUT Intput Output Numeric value output IODATA 30 ms or more Program number When the output request of a line number override value or error number was input Program number output request PRGOUT Outputting program number PRGOUT Intput Output Num...

Страница 442: ...r output request ERROUT Outputting error number ERROUT Intput Output Numeric value output IODATA 30 ms or more Jog enable input JOGENA Output during jog enabled JOGENA Intput Output Jog mode Replies the setting value of the jog mode input signal with jog mode output Jog mode input JOGM Jog mode output JOGM Intput Output 30 ms or more Jog mode Jog operation axis 8 axes on jog feed plus side JOG Int...

Страница 443: ...input signal status of the hand Mechanical n hand input signal status HNDSTSn Output Hand input signal status Mechanical n hand error input HNDERRn Output during mechanical n hand error occurrence HNDERRn Intput Output Mechanical n pneumatic error input AIRERRn Outputting mechanical n pneumatic error AIRERRn Intput Output Within the user specified area User specified area 8 points USRAREA Output I...

Страница 444: ...Output Numeric value output Operating status output Waiting status output Program selection enabled output Cycle stop operating status output signal Error occurring status output signal IODATA PRGSEL START STOP IOENA SLOTINIT CYCLE ERRRESET IOENA IODATA START STOP SLOTINIT ERRRESET PRGOUT CYCLE 1 2 3 1 2 3 Error occurring status Program selection Program start Stop Restart Stop Program reset Error...

Страница 445: ...RGOUT OVRDSEL OVRDOUT LINEOUT START SRVON IODATA IOENA START SLOTINIT SRVOFF IOENA 1 80 50 5 80 50 0 1 5 5 Program No 1 Program No 5 Operation rights request Servo ON Servo OFF Override output Override selection Program start Program selection Program No output Override selection Program END Line No output Program start Line No output Program No output Program selection input signal Input Numeric ...

Страница 446: ... ON input signal Servo OFF input signal Error reset input signal General purpose output signal reset Program reset Operation rights input signal General purpose output Input Operation rights output signal Emergency stop output signal Operation rights request Program start Program start Servo ON Servo OFF Servo ON Servo ON Servo ON Restart Restart Emergency stop ON Error reset Error reset Error occ...

Страница 447: ... Output Recovery work In servo ON Jog enable input signal Jog mode input Jog mode output In servo OFF Operation rights request Servo ON Program start H Error occurrence Servo ON Jog command J1 Jog command J2 Jog command end Jog command Z Jog command end Safe point return start Safe point return end Program reset Program start Start input Servo ON input signal Error reset input signal Operation rig...

Страница 448: ...p basic operation and maintenance 6 6 1 Robot Behavior upon Emergency Stop Input When an emergency stop signal is input while the robot is operating the servo power supply is cut off by means of hardware control The robot s tip path and stopping position after the input of an emergency stop signal cannot be specified An overrun may occur depending on the robot speed or load condition of the tool ...

Страница 449: ...１０ to Ｘ１７５ Input 16 to 23 8 bit Job number input MWORK M_INB 16 Production qty output 16 bit M_OUTW 16 MCOUN Job number Item Item Item No of I Os 256 inputs 256 outputs The device names as viewed from GOT are X00 to XFF and Y00 to YFF Refer to Robot I O and GOT assignment described later GOT connection qty １ Multiple GOT units cannot be connected to a single robot controller however multiple robo...

Страница 450: ...15 J71E71 100 Cross cable for direct connection Straight cable for hub course 100BASE T LAN cable Cross cable for direct connection GOT1000 series Ethernet communication unit GT15 J71E71 100 LAN1 Straight cable for hub course CR2n 700 series R700CPUユニット 100BASE T LAN cable LAN1 GOT1000 series Ethernet communication unit GT15 J71E71 100 Cross cable for direct connection Straight cable for hub cours...

Страница 451: ... with a communication cable USB set Communication setting to USB at Communication Communication with GOT in the GT Designer2 menu select Project download GOT check the import data import to GOT and then check the operation 5 Assignment of I O signal numbers I O numbers 0 to 255 are used at GOT I O numbers 0 to 255 are common for the parallel I O interface parallel I O unit and GOT If the customer ...

Страница 452: ... interface Station no setting rotary switch of parallel I O unit GOT1000 XY devices as viewed from GOT ０ 0 to 31 Option slot １０ X00 X1F Y00 Y1F １ 32 to 63 Option slot２１ X20 X3F Y20 Y3F ２ 64 to 95 Option slot３２ X04 X5F Y40 Y5F ３ 96 to 127 ３ X60 X7F Y60 Y7F ４ 128 to 159 ４ X80 X9F Y80 Y9F ５ 160 to 191 ５ XA0 XBF YA0 YBF ６ 192 to 223 ６ XC0 XDF YC0 YDF ７ 224 to 255 ７ XE0 XFF YE0 YFF ...

Страница 453: ... flange in comparison with the plane through the J1 axis vertical to the ground Q is center of J5 axis rotation in comparison with the plane through the J1 axis vertical to the ground Fig 7 1 Configuration flag Right Left 2 ABOVE BELOW Q is center of J5 axis rotation in comparison with the plane through both the J3 and the J2 axis Fig 7 2 Configuration flag ABOVE BELOW 5 axis type 6 axis type LEFT...

Страница 454: ...nly This means in which side the J6 axis is in comparison with the plane through both the J4 and the J5 axis Fig 7 3 Configuration flag NONFLIP FLIP FLIP NON FILIP J4 axis J6 axis flange surface FL1 Flag1 B 0 0 0 0 0 0 0 0 1 0 NONFLIP FLIP Note B is shows the binary ...

Страница 455: ...ft Indicates the location of the end axis relative to the line that passes through both the rotational center of the J1 axis and the rotational center of the J2 axis Fig 7 4 Configuration flag Right Left RIGHT LEFT FL1 Flag1 B 0 0 0 0 0 0 0 0 1 0 Right Left Note B is shows the binary ...

Страница 456: ...9 443 Configuration flag 7Appendix ...

Страница 457: ......

Страница 458: ...d in Japan on recycled paper Specifications are subject to change without notice HEAD OFFICE TOKYO BUILDING 2 7 3 MARUNOUCHI CHIYODA KU TOKYO 100 8310 JAPAN NAGOYA WORKS 5 1 14 YADA MINAMI HIGASHI KU NAGOYA 461 8670 JAPAN ...

Отзывы:

Нет отзывов

Похожие инструкции для MELFA CR1D

FEPL-02 Ethernet POWERLINK

Бренд: ABB Страницы: 2

Бренд: ABB Страницы: 2

Бренд: Microchip Technology Страницы: 37

Бренд: S-COM Страницы: 400

Бренд: Samsung Страницы: 27

Бренд: VADDIO Страницы: 2

Бренд: Watlow Страницы: 59

Tekmar WiFi Snow Melting Control 670

Бренд: Watts Страницы: 48

Бренд: YASKAWA Страницы: 49

Бренд: M-system Страницы: 17

GRASS VALLEY MDX-3901

Бренд: Belden Страницы: 45

Бренд: Klimaire Страницы: 5

Бренд: Measurement Computing Страницы: 32

Бренд: TEL Страницы: 26

Бренд: Vimar Страницы: 32

Бренд: Vertiv Страницы: 2

Бренд: Quantum Страницы: 20

Бренд: Aurora Страницы: 2

Бренды по названию

0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Популярные бренды

Загрузить еще бренды