Pump characteristics and data
l
V_g: Geometric displacement volume (
P 2851[0]
(ccm/rev))
l
eta_Vol,N: Volumetric efficiency at the pump’s rating point (
P 2851[4]
(%))
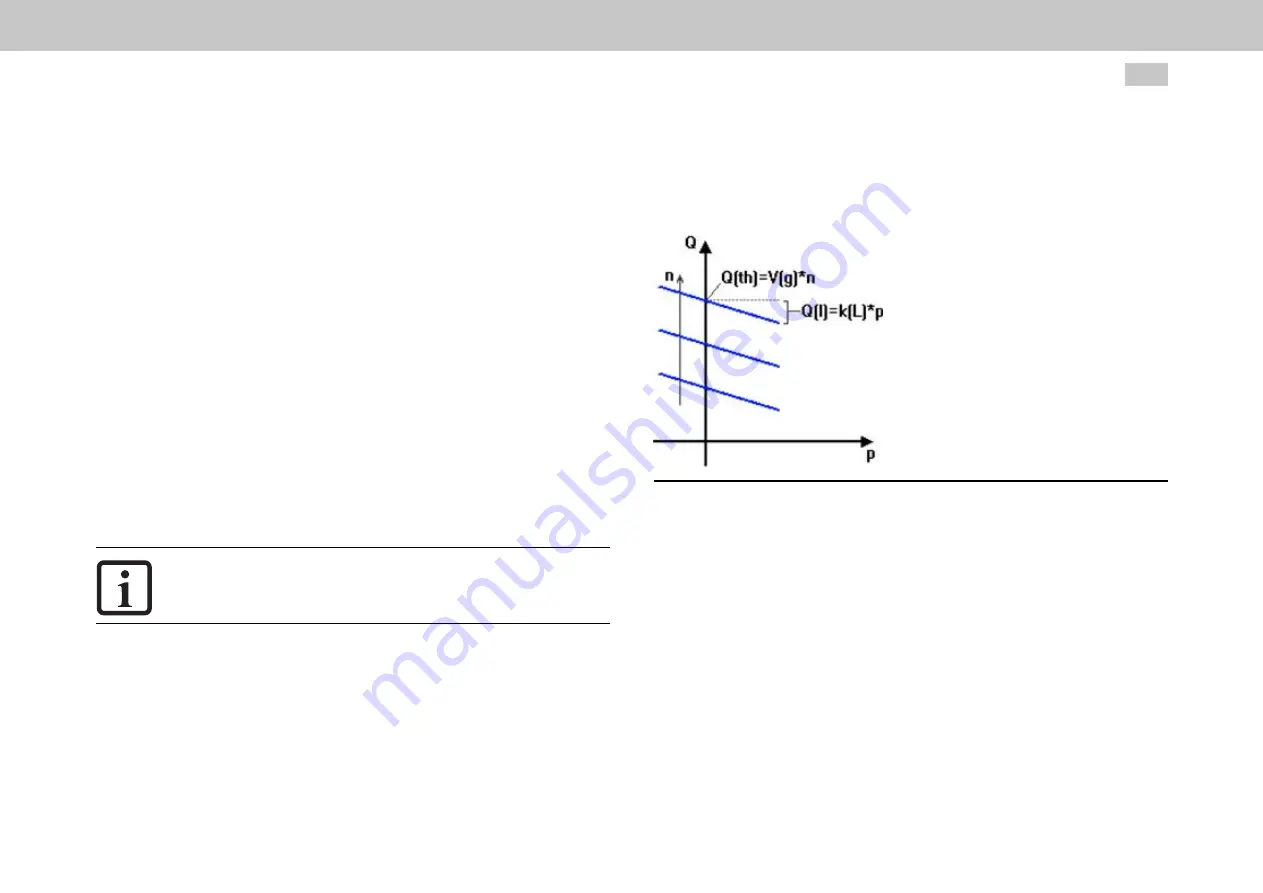
Theoretical volumetric flow rate Q_th is proportional to the speed:
l
Q_th = V_g ∙ n
Internal pump leakage volumetric flow rate Q_L must be subtracted from the actual
volumetric flow rate:
l
Q = Q_th - Q_L = V_g ∙ n - Q_L
It will typically be proportional to the pressure:
l
Q_L = p ∙ k_L(ϑ)
However, pump data sheets often do not specify the leakage volume rate constant,
but instead specify a “volumetric efficiency” ηvol,N for the pump’s rated point, in
which case:
l
Q_N = V_g ∙ n_N ∙ η_(vol,N)
l
Q_N [l/min] = V_g [cm³/rev] ∙ n_N [rev/min] ∙ eta_(Vol,N) [100 %]
NOTE
l
Make sure to convert to SI units!
Example
l
eta_(Vol,N) = 95 %, n_N = 1500 rev/min, v_G = 10 cm³/rev -> Q_N =
14,2 l/min
MOOG
ID No.: CB40859-001 Date: 11/2020
MSD Servo Drive - Device Help
175
7 Control
If you specify eta_(Vol,N), the servo drive will internally calculate k_L automatically
as follows:
l
k_L = V_g ∙ n_N ∙ (1 - eta_(Vol,N) ) ∙ p_N
Image 7.52: Pump characteristic curves
For the torque at the pump (= motor torque):
l
M = V_g / 2π ∙ p + (M_friction); (make sure to use SI units)
The friction torque is normally unknown and negligible (M_friction ~ 0). This means
that a “torque constant” c_M in [Nm/bar] can be calculated using the following
formula:
l
c_M [Nm/bar] = 1/(20pi) * V_g [cm^3/rev] = M [Nm] / p [bar]
Displacement volume V_g is usually specified in data sheets. In contrast, if there is a
pressure measurement available, the torque constant is easier to determine
experimentally if necessary. In this case, a constant pressure can be built up on the
drive in a steady state and the delivered motor torque can be used to calculate the
displacement volume.






























