Yamaha FLIP-X Series, User Manual

Page: 129 / 130

Appendix
v
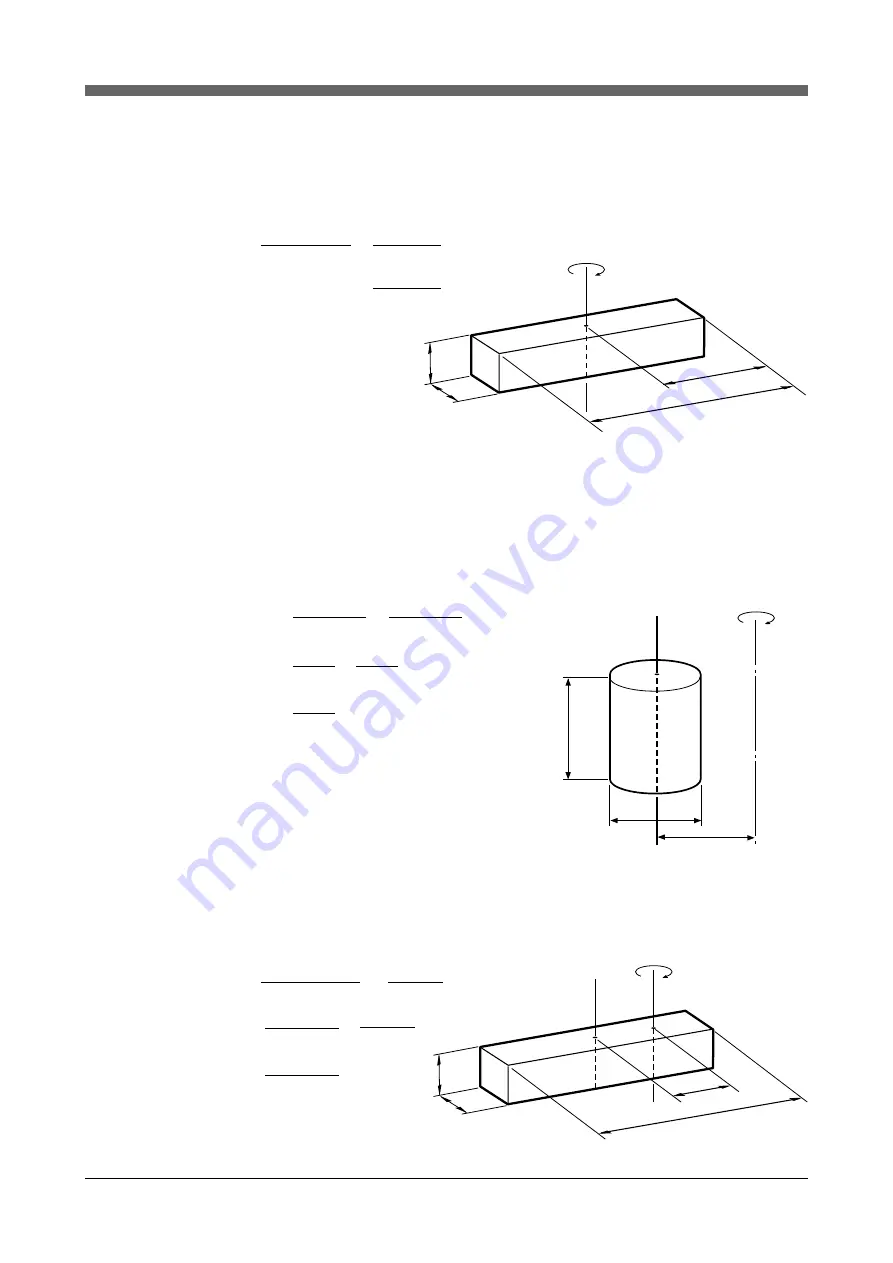
2. Moment of inertia for rectangular parallelepiped
The moment of inertia (J) for a rectangular parallelopiped having a rotation center as shown
below is given by
J =
ρ
abc (a
2
+ b
2
)
12g
W (a
2
+ b
2
)
12g
= (kgf.cm.sec
2
)
m (a
2
+ b
2
)
12
= (kgm
2
)
: Density (kg/cm
3
)
: Gravitational
acceleration (cm/sec
2
)
: Weight of prism (kgf)
: Mass of prism (kg)
a
c
b
1/2a
ρ
g
W
m
3. When the object’s center line is offset from the rotation center.
The moment of inertia (J) when the center of the cylinder is offset by a distance “x” from the
rotation center as shown below is given by
D
h
J =
ρπ
D
4
h
32g
WD
2
8g
= (kgf.cm.sec
2
)
: Weight of cylinder (kgf)
: Mass of cylinder (kg)
: Density (kg/cm
3
)
: Gravitational acceleration (cm/sec
2
)
x
+
ρπ
D
2
hx
2
4g
+
Wx
2
g
mD
2
8
= mx
2
(kgm
2
) +
center line
rotation
center
W
m
e
g
In the same manner, the moment of inertia (J) of a prism as shown below is given by
J =
ρ
abc (a
2
+b
2
)
12g
W(a
2
+b
2
)
12g
=
: Weight of prism (kgf)
: Mass of prism (kg)
a
c
b
x
center line
+
ρ
abcx 2
g
Wx
2
g
+
(kgf.cm.sec
2
)
m(a
2
+b
2
)
12
=
+ mx
2
(kgm
2
)
W
m