vi.
Clear the current contents of the
screen using
SHIFT ALPHA CLEAR
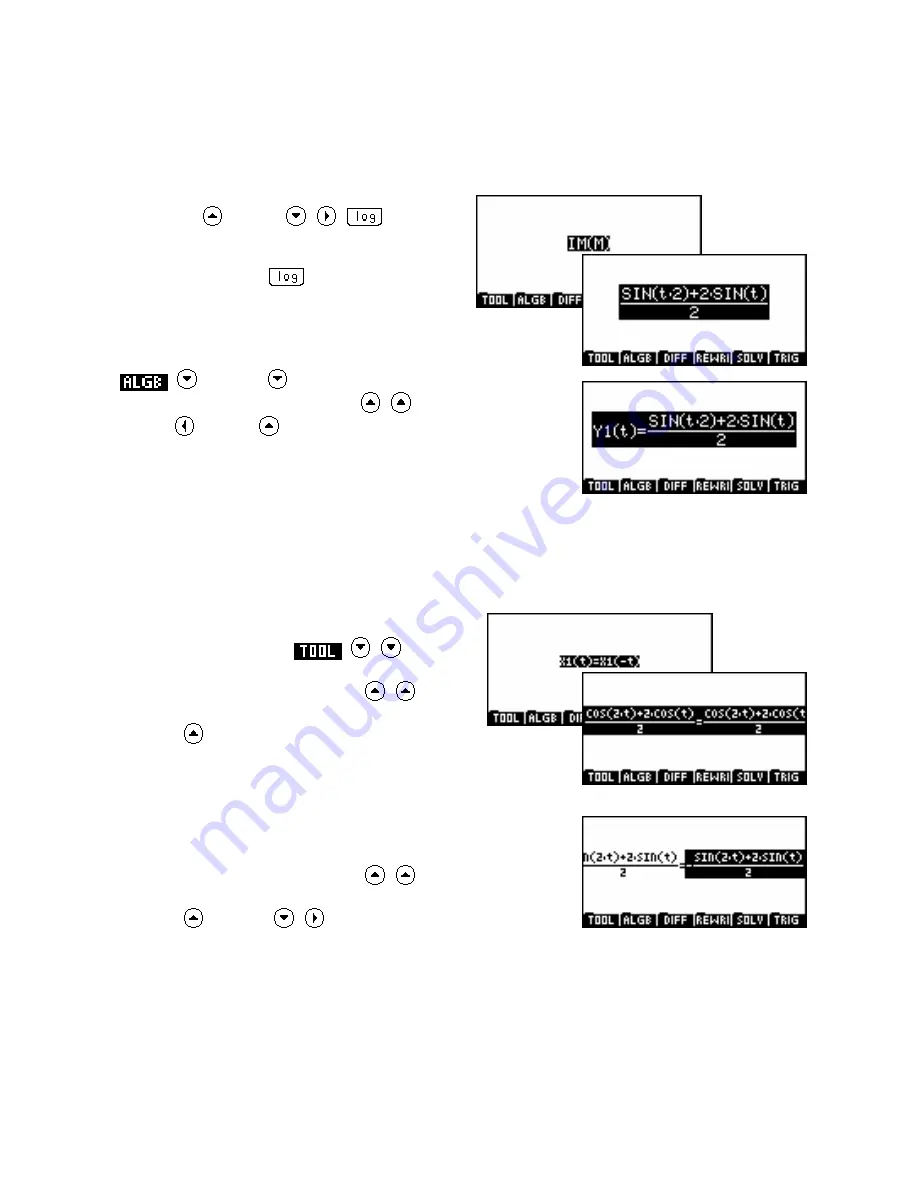
. Then perform the same definition assignment for
Y1(t)
as the
imaginary part of
M
.
ALPHA M
MATH
ENTER ENTER
Note:
As before, the
button jumps to the first
function with that letter (
L
), in this case
IM
.
ENTER
SHIFT =
ALPHA Y 1 ( ALPHA SHIFT T
SHIFT
SHIFT
ENTER
vii.
In order to show that the function is symmetrical about the x axis we need to show that
(X1(-t),Y1(-t))
is
equivalent algebraically to
(X1(t), -Y1(t))
. Purely for convenience we will display
X1(t)=X1(-t)
and
evaluate each side. The = is not used to solve anything but just to display both at once for comparison so
that it can be seen whether or not they are equal as required. To aid in this, we will change to the small
l
SHIFT ALPHA CLEAR
ALPHA X 1 ( SHIFT ALPHA T
SHIFT =
T (-)
SHIFT
ENTER
We now
font, c earing the screen first.
ALPHA X 1 ( SHIFT ALPHA
As can be seen, the two are algebraically equivalent.
check the same equality for
Y1
, again clearing the screen first.
SHIFT ALPHA CLEAR
ALPHA Y 1 ( SHIFT ALPHA T
SHIFT = ALPHA Y 1 ( SHIFT ALPHA T (-)
SHIFT
ENTER
Again it is clear that the condition that
Y1(t)= -Y1(-t)
has been met. Therefore we can conclude that the
graph is symmetrical about the x axis.
354



























