S
S
o
o
l
l
v
v
i
i
n
n
g
g
s
s
i
i
m
m
u
u
l
l
t
t
a
a
n
n
e
e
o
o
u
u
s
s
e
e
q
q
u
u
a
a
t
t
i
i
o
o
n
n
s
s
.
.
Solve the systems of equations below:
2
x
y
=
4
−
−
3
2
x
y
= −
7
⎫
3
x
y
z
(i)
⎬
(ii)
− +
2
−
= −
10.5
+
4
x
y
=
2
⎭
−
3
+
x
y
z
=
10.5
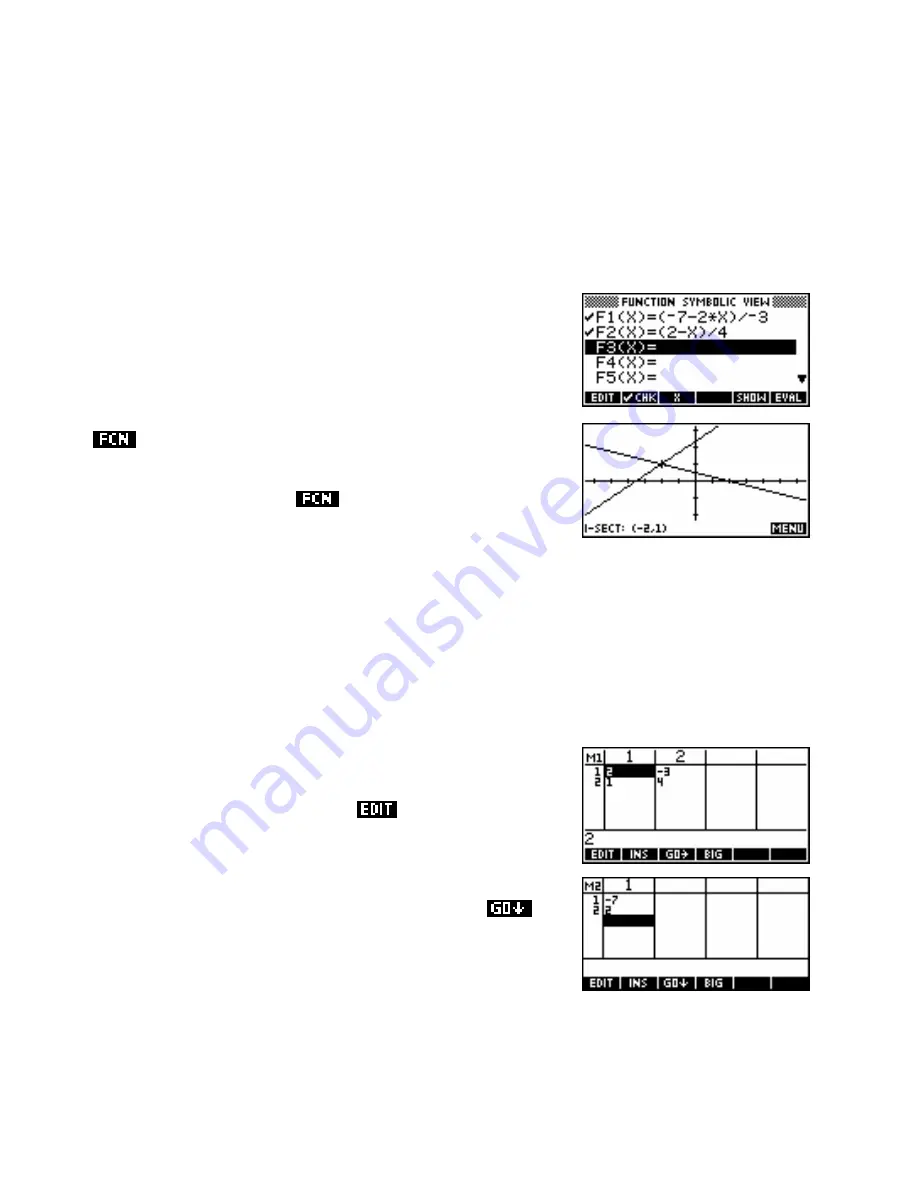
Method 1 - Graphing the lines
Because the first set of equations is a 2x2 system it can be graphed in
the Function aplet. To do this it is necessary to re-arrange the functions
into the form y = …… and store them into
F1(X)
and
F2(X)
in the
SYMB
view of the Function aplet. Switch to the
PLOT
view and use the
Intersection
tool to find the point of intersection.
It is worth noting that although the point of intersection is on the screen
here, this is not necessary. The
Intersection
tool will work even
if neither line is visible on the currently set axes.
Method 2 - Using a matrix
−
3
x
2
x
y
= −
7
⎫
⎡
2
−
3
⎤ ⎡
⎤
⎡−
7
⎤
Step 1. Rewrite
x
y
=
2
⎭
as
⎣
1
4
⎦ ⎣
⎦
=
⎣
2
⎦
⎥
⎬
⎢
⎥ ⎢
⎥ ⎢
+
4
y
x
⎡ ⎤
⎡
2
−
3
⎤
−
1
⎡−
7
⎤
This means that
⎢ ⎥ = ⎢
× ⎢
y
⎣ ⎦
⎣
1
4
⎦
⎥
⎣
2
⎦
⎥
Step 2. Switch into the Matrix Catalog (
SHIFT MATRIX
). Position
the highlight on
M1
and press
. Enter the matrix shown
right.
Press
SHIFT MATRIX
to change back to the catalog view and
create
M2
as shown below right. Note that setting
will
make it easier to enter
M2
.
302






























