HP 39gs Master Manual Download Page 120

Page: 120 / 366

New columns as functions of old

You have already seen the use of one trick when we created a new column

by storing

2*C1

into

using

the

HOME

view. This can be used to create new columns as functions of any number of others. For example,

a set of data that you suspect is exponential could be ‘straightened’ by storing

LN(column)

into a fresh

column. Changes of scale and origin can be investigated in this way by storing (say)

-2*C1 + 3

into

You can even combine columns such as

C1 + C2

If you don’t particularly need to

see

the data as a fresh column, you can

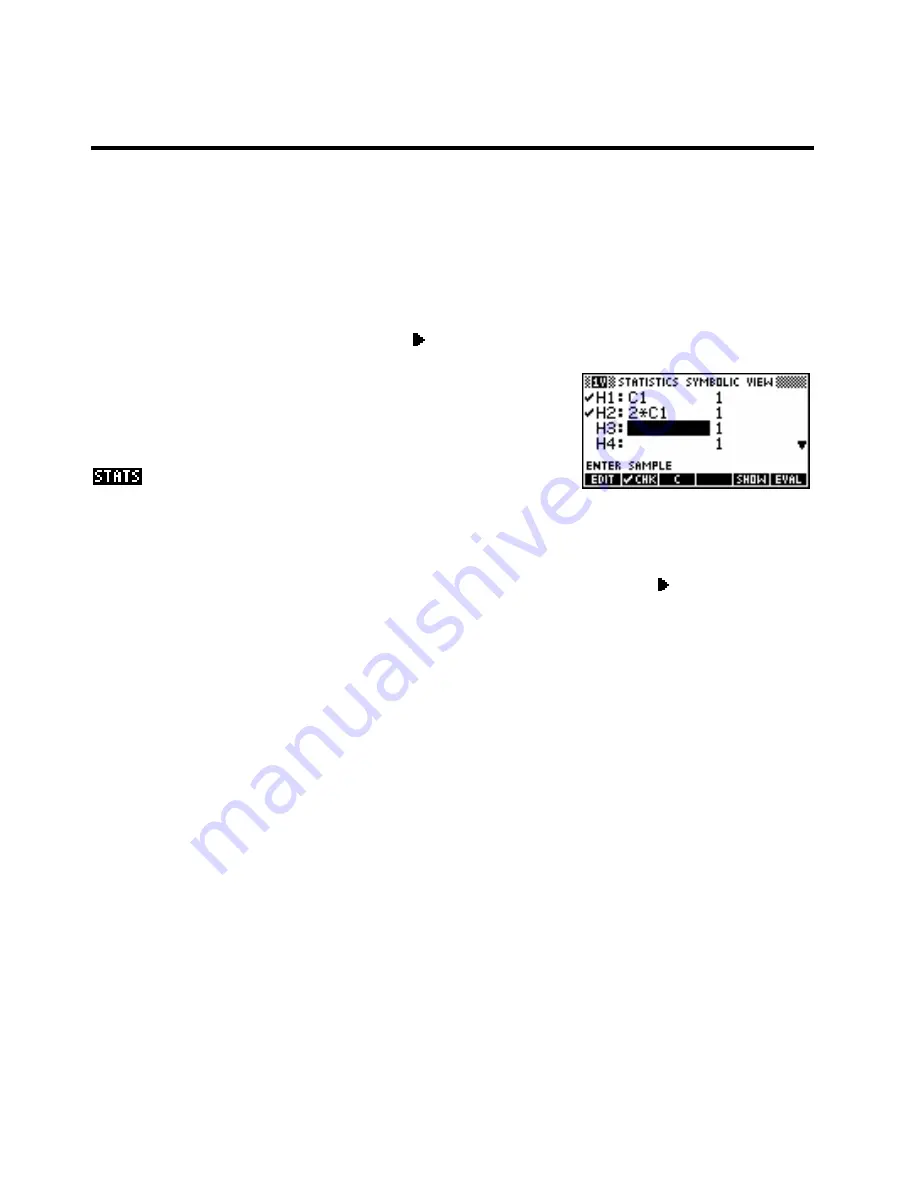
use the

SYMB

view to accomplish the same thing in a simpler way. For

example, the

SYMB

view snapshot on the right would accomplish the

same thing as storing

2*C1

into

. A histogram of

would look the

same as the one we produced earlier using the

HOME

view, and the

command would give exactly the same results. The advantage

of this is that it takes much less memory if both columns need not be stored.

For the teacher this can be a handy way to create sets of data that conform to particular models. For

0.03

example, if you would like a set of data that conforms to a model of

2.5

then simply enter any

values randomly into

and then, in

HOME

, perform the calculation

2.5*e^(0.03C1) C2

. Of course, the

result will be a set of y values which exactly match the model and this is not desirable. The teacher should

now go through them and introduce some random error so that they are no longer a perfect fit.

Simulating Dice

The most common experiments in probability involve the rolling of dice. This can be simulated in the Statistics

aplet using the

MATH

menu function

MAKELIST

. (For more detail see page 190)

The syntax is:

MAKELIST( expression, variable name, start, end, increment )

where

expression

is the mathematical rule used to
generate the numbers.

variable name

is the letter (X, Y etc.) that is to be
used

the

expression

(any

other

letters will be taken as constants).

tart

is the first value

variable name

is to take.

is the upper bound for

variable name

and

increment

is the amount that variable name
should be incremented by in each

iteration.

For example:

MAKELIST(X2,X,1,10,2)

would produce { 1, 9, 25, 49, 81 } as

went from 1 to 3 to 5 to …

120

Summary of Contents for 39gs

Page 1: ...hp 39gs and hp 40gs graphing calculators Mastering the hp 39gs hp 40gs A guide for teachers students and other users of the hp 39gs hp 40gs Edition 1 0 HP part number F2224 90010 ...

Page 2: ... BE LIABLE FOR ANY ERRORS OR FOR INCIDENTAL OR CONSEQUENTIAL DAMAGES IN CONNECTION WITH THE FURNISHING PERFORMANCE OR USE OF THIS MANUAL OR THE EXAMPLES CONTAINED HEREIN Copyright 2006 Hewlett Packard Development Company L P Reproduction adaptation or translation of this manual is prohibited without prior written permission of Hewlett Packard Company except as allowed under the copyright laws Hewl...

Page 3: ...other aplets from the HOME view 40 A brief introduction to the MATH Menu 41 Resetting the calculator 42 Summary 45 The Function Aplet 46 Auto Scale 49 The PLOT SETUP view 50 The default axis settings 52 The Bar 52 The Menu Bar functions 53 The FCN menu 57 The Expert Working with Functions Effectively 62 The VIEWS menu 85 Downloaded Aplets from the Internet 91 The Parametric Aplet 92 The Expert Vec...

Page 4: ...2 The MATH menus 165 Accessing the MATH menu commands 166 The PHYS menu commands 168 The MATH menu commands 169 The Real group of functions 170 The Stat Two group of functions 178 The Symbolic group of functions 179 The Tests group of functions 182 The Trigonometric Hyperbolic groups of functions 182 The Calculus group of functions 184 The Complex group of functions 186 The Constant group of funct...

Page 5: ...t 245 Using downloaded aplets 249 Deleting downloaded aplets from the calculator 250 Capturing screens using the Connectivity Kit 251 Editing Notes using the Connectivity Software 252 Programming the hp 39gs hp 40gs 255 The design process 255 Planning the VIEWS menu 257 The SETVIEWS command 259 Example aplet 1 Displaying info 262 Example aplet 2 The Transformer Aplet 268 Designing aplets on a PC 2...

Page 6: ...311 Inference testing using the Chi2 test 312 Appendix B Teaching or Learning Calculus 314 Investigating the graphs of y xn for n an integer 314 Domains and Composite Functions 315 Gradient at a Point 317 Gradient Function 318 The Chain Rule 319 Optimization 319 Area Under Curves 320 Fields of Slopes and Curve Families 320 Inequalities 321 Rectilinear Motion 321 Limits 321 Piecewise Defined Functi...

Page 7: ...gs shown above are sister calculators released in 2006 They are identical in almost all respects except for their color schemes and in whether they have infra red or a CAS The hp 39gs was released mainly in the United States and other regions such as Australia which do not allow a Computer Algebra System or CAS in their educational systems The hp 40gs on the other hand was released mainly in Europ...

Page 8: ...rhaps on the Expert User chapters This book provides a supplement to the official manual and more importantly expert tips to make your work smother and more confident It has been designed to cover the full use of the hp 39gs and hp 40gs calculators This means explanations which will be useful to anyone from a student who is just beginning to use algebra seriously to one who is coming to grips with...

Page 9: ... this bar for special functions in any given context The SYMB key nearly always takes you to a view in which you can enter equations The PLOT key displays the graph view for any given environment HOME is where you will do most of your calculations It is shared by all the aplets and oversees them all The NUM key gives you a tabular view of your function sequence or data These are the arrow keys The...

Page 10: ... the bottom of the various screens how the meanings of the row of unlabelled screen keys change in different views The SYMB key in this case it is set to graph 3 the function f x x2 7x 6 x The PLOT key used to graph the function The PLOT SETUP view sets the axes The NUM key showing a tabular view of the function The NUM SETUP view sets table parameters The APLET key is used to choose which aplet i...

Page 11: ... need the SHIFT key or not are written in this typeface KEY The SHIFT and ALPHA keys The SHIFT key gives you the second function for each key In the case of the COS key the second function is ACOS sometimes referred to as arc cos or cos 1 or inverse cos Most keys have these second functions that are obtained via the SHIFT key Note When I want you to use one of these keys that needs to have the SHI...

Page 12: ...As an example I might say to press and choose Chronologically The manual you are given with your calculator uses a different convention As mentioned before the third way a key can be used is to get letters of the alphabet This is not so that you can write letters to your friends although you can do that with the Notepad but so that you can use variables like X and Y or A and B The key above the SH...

Page 13: ...e left side of the menu lists the categories of functions As you use the up down arrows to scroll through the topics you ll see the actual list on the right change Move down through the menu until you reach Prob short for Probability and then one step more and you ll find yourself back at Real Now press the right arrow key and your highlight will move into the right hand menu see above Move the hi...

Page 14: ... These aplets are The Finance aplet see page 155 Performs calculations involving time value of money The Function aplet see page 46 Provides f x style graphs calculus functions etc It will not only graph but find intercepts intersections areas and turning points The Inference aplet see page 141 Allows the investigation of inferential statistics via hypothesis testing and confidence intervals The L...

Page 15: ... best fit linear and non linear The Triangle Solve aplet see page 152 This aplet solves for sides and angles in triangles The Trig Explorer aplet see page 162 This is a teaching aplet allowing the student to investigate the properties of sine and cosine graphs in the same interactive fashion as the Quadratic Explorer The Function aplet is probably the easiest to understand and also the one you wil...

Page 16: ...ving said that aplets are best thought of as working environments it is equally true that aplets are essentially programs with the standard ones simply being built into the calculator This is a programmable calculator having its own programming language and able to perform quite sophisticated tasks Unless you particularly want to learn about the programming language there is no reason why you shou...

Page 17: ...ns the distance over which the infra red link can communicate is limited to about 8 10cm about 3 4 inches See page 237 for details on this process The hp 40gs does not have infra red because some of the markets for which it was produced did not wish students to have this capability Aplets are available to do many mathematical tasks such as statistical simulations time series analysis as well as ma...

Page 18: ...e H HO OM ME E v vi ie ew w This is the HOME base for the calculator All other aplets can be accessed from it and can affect it to varying degrees All mathematical functions are available in this view You should learn to use this view as efficiently as possible since a great deal of work will be done here We will explore the HOME view in the following order Exploring the Keyboard Angle and numeric...

Page 19: ...of each key is listed in the row of boxes at the bottom of the screen A common abbreviation used for these keys is SK1 or SK2 etc for screen key 1 In the PLOT view shown right some of the screen keys are labeled such as the key When you press this key the row of screen keys labels in the PLOT view appear or disappear To see another view where all the keys are in use change to the APLET view Calcul...

Page 20: ...gle and numeric settings are tied to the active aplet Changing aplets may therefore cause these settings to change in In addition to the standard twelve covered in great detail in the chapters following many more aplets are available from the Internet written by other programmers Once these are downloaded into your calculator they can also be accessed via the APLET key For more detail on this type...

Page 21: ...tion on the VIEWS menu is given in the chapter dealing with the Function aplet In its second role the VIEWS key also has a critical purpose when using aplets which have been downloaded from the Internet When a programmed aplet is created for the hp 39gs or hp 40gs a menu is provided by the programmer to let you control and use it During the programming this menu is tied to the VIEWS key replacing ...

Page 22: ...he more common functions have keys of their own but there is a limit to the number of keys that one can put on a calculator before it takes too long to find the key required Hence the MATH key The MATH menu lists all those functions that would not fit onto the keyboard plus some which also appear on the keyboard Shown in the screen snapshot right is a small selection of the total list For a listin...

Page 23: ...different aplets so for more information see the explanations in the chapters dealing with the various aplets particularly in the Function aplet on page 50 The SYMB SETUP key is only used in one place which is to choose the data model for bivariate statistics in the Statistics aplet It is not available in the other aplets and trying to access it will result only in a quick flash of an exclamation ...

Page 24: ...can be a little annoying to constantly have 12 significant figures displayed In Standard mode very large and very small numbers are displayed in scientific notation The Fixed Scientific and Engineering formats all require you to specify how many decimal places to display The screenshot right shows Fixed 4 which rounds everything off to 4 decimal places Of course you can change the 4 to any other n...

Page 25: ...is used instead of a decimal point If you opt to use a comma rather than a full stop then any places where a comma would normally be used such as in lists will swap to using a full stop Any functions which might normally have terms separated by a comma will use a full stop instead For example ROUND 3 456 2 will become ROUND 3 456 2 key on most ators press the Above the ENTER key is the ANS d norma...

Page 26: ...he above calculation then the calculator will display Ans 2 The reason for this is that a subtract cannot start an expression in mathematics while a negative sign can Since the subtract can t come first the calculator decides that you must have intended to subtract from the previous answer Hence the sudden appearance of an Ans This occurs at other times too A common error by new users is to enter ...

Page 27: ...as a kind of super delete key For example if pressing DEL would erase one function only in the SYMB view then CLEAR will erase the whole set Calculator Tip Another use for the DEL For example MODES then pressi DEL lt of Radians Pressing CLEAR in the MODES view would restore factory settings to all the view key is to restore factory settings if you move back into the screen and change to Degree mod...

Page 28: ...only for the aplet but in the HOME view too For example suppose you have been performing trig calculations in the HOME view with the Function aplet being currently active and have set the angle measure to DEG If you were to now change to the Solve aplet in order to solve an equation then the settings would revert to those of the Solve aplet probably be radians unless you had also changed those as ...

Page 29: ...ult setting of degrees and its setting was independent of those of the aplet This meant that a calculation such as the one above would give incorrect results and caused considerable confusion to some students It even resulted in users returning their hp 38g to dealers as being faulty Hence the change which was first made in the hp 39g and hp 40g The only drawback of synchronizing the settings of t...

Page 30: ...roblem has been addressed on the hp 39gs and hp 40gs in two ways Both have a very ample amount just short of 200Kb and there are very few users who will come close to filling this Depending on size there is enough room for at least 40 aplets 40 pages of notes or nearly 10 000 data points although not of course all at once In addition to all this memory the hp 39gs and hp 40gs supply an easy way to...

Page 31: ... for the aplet in the APLET view but will not usually be a very large amount as you can see in the examples shown Calculator Tip APLET view the helper shared by other aplets APLET view Even on The reason for this naming convention for helper programs is that when you delete the parent aplet in the programs are NOT automatically deleted with it because they may be You must change to the Program Cat...

Page 32: ... internet are listed in the APLET view along with the normal aplets and when you delete them the associated library is automatically deleted with them unlike the case of the helper programs Calculator Tip 1 l 2 l l Because of the amount of memory available on the hp 39gs hp 40gs the Memory View is not one that you will normally need to worry about unless you store a tru y amazing number of Notes I...

Page 33: ...decimals like 0 25 are easy to convert to a fraction others such as recurring ones are not so easy Most calculators opt for the easy option of switching to a decimal answer in any mixture of fractions and decimals When making the hp 39gs and hp 40gs HP took a very different approach Once you select Fraction mode all numbers become fractions including any decimals The first point to remember is tha...

Page 34: ...of approximation which matches the decimal to that number of significant digits For example a setting in the MODES view of Fraction 1 3 changes 0 234 to 13 which is actually 0 2307692 matching to at least 1 significant figures Fraction 2 7 changes 0 234 to 30 which is actually 0 2333333 matching to at least 2 significant figures Fraction 3 11 changes 0 234 to 47 which is actually 0 2340425 matchin...

Page 35: ...f Mixed Fraction is essentially the same but answers are given as mixed fractions instead of improper fractions as shown If you want to use the Fraction setting to convert decimals to fractions here are some tips if converting a recurring decimal to a fraction then make sure you include at least one more digit in the decimal than the setting of Fraction in MODES As you can see right failing to inc...

Page 36: ...fact a Fraction 6 setting tends to be more reliable A new feature of the hp 39gs and hp 40gs is the setting of Mixed Fraction in the MODES view The results of this new setting can be seen in the image to the right 1 Using the setting of Mixed Fraction the result is 4 1 7 4 7 whereas the answer of 29 7 is obtained using the old Fraction setting Calculator Tip 4 1 7 If you scroll back through the Hi...

Page 37: ...may have noticed that as soon as the highlight appeared so did two labels at the bottom of the screen If you now press the screen key under you will find that the highlighted calculation will be copied on the edit line This is shown in the screen shot on the right At this point you can use the left and right arrows and the DEL key to edit the calculation by removing some of the characters and or a...

Page 38: ...splay an expression the way you would write it on the page rather than in the somewhat difficult to read style that is forced on the calculator when it must show the whole expression on one line This works anywhere the Next to the label appears not just in HOME Some examples 38 ...

Page 39: ...l do this in two stages calculating the top and bottom of the fraction and storing the results in memories Firstly the top of the fraction storing the result in memory A then the bottom storing in B and then finally the result As another example suppose we were evaluating 3x x2 7 for the value x 3 We can store 3 into the memory X and then use that symbol in the calculation as shown right The advan...

Page 40: ...e QUOTE X 2 rather than just X 2 is that using X 2 would tell the calculator to use the value currently stored in memory X while QUOTE X 2 tells it to use the symbol The QUOTE function is available through the MATH menu under Symbolic see page 181 Note This type of work is actually far more easily done in the Function aplet where QUOTE is not needed and the key does a better job See page 64 e g 2 ...

Page 41: ...hand menu is a list of topics Scroll through the topics until you find the one you want then use the right arrow key to move into the list of functions for that topic For example The function ROUND will round off to a specified number of decimal places E g round off 145 25667 to 3 decimal places Press the MATH key right arrow into the Real group of functions Press the R key the 9 key to move to th...

Page 42: ...then redisplay the HOME view with the Function aplet as the active one If you find that the calculator locks up so completely that the keyboard will not respond then a method of reset is provided below which is independent of the keyboard This shouldn t happen but it is important to know how to deal with it in case it happened during a test or an exam Soft reboot Hardware Thi s method is provided ...

Page 43: ...d to lock up occasionally particularly if you load aplets and programs I usually suggest to my students that they regularly save their work to a PC and perform a hard reboot about once a month reloading the saved work onto the calcu Pressing by mistake will result in the screen shown right This is a special diagnostic mode that can be used by engineers to There is nothing wrong with experimenting ...

Page 44: ...e sensation of pressing a button as the paperclip shorts out the batteries momentarily Could you have accidentally bent the shorting contact last time you used a paperclip so that it is permanently shorting out Check the battery compartment Are any of the metal contacts broken or out of place Are the batteries firmly in contact with all of them Is anything out of place Do any of the batteries or t...

Page 45: ...any views The MODES view can be used to set the format in which numbers are displayed on the HOME page and to choose the angle measure which is to be used Make sure you understand Fraction mode before using it Remember that the angle and numeric mode settings may change if you change aplets in the APLET view Numbers are stored in memory using the key labeled The stored values can then be used by s...

Page 46: ...s such as f g x or f x 2 The first step for any aplet is to choose it in the APLET LIBRARY Press the APLET key and you will see something similar to the screen on the right Use the arrow keys to move the highlight up or down until the Function aplet is selected Now looking at the list of context sensitive functions at the bottom of the screen you should see labels of and Press the key under first ...

Page 47: ...r section on the HOME view Using the up down arrows move the cursor if necessary to the line labeled F1 X Type in This will produce the screen shown on the right Notice the check tick mark next to the F1 X that appeared when you pressed ENTER This signifies that this function is to be graphed so that if you had five functions entered but only wanted 1 and 3 graphed you could simply ensure that onl...

Page 48: ... This is covered in detail on page 70 Now press the PLOT key The graph you ll see will not be a terribly useful one see right because the axes will not be set up correctly We ll look next at how to do this One of the easiest ways to set up the axes properly for a function whose shape is not known in advance is to let the calculator suggest a suitable scale using the Auto Scale option in the VIEWS ...

Page 49: ...u ve not chosen the domain wisely then your result may not be good it doesn t choose nice scales for the y axis such as we would choose going up in 0 2 s or 5 s or 10 s etc so you will generally need to tidy up its choice a little If you look at the y axis of the graph you ve just produced you ll see that the axis tick marks are so close together that it looks like a solid line To tidy this up you...

Page 50: ...ution If you highlight it and press the key you will see that you have a choice of Faster or More Detail More Detail should be selected If you choose Faster then every second dot is plotted instead of every dot This is quicker but may make some graphs appear less smooth particularly graphs with steep gradients There are two pages to this view see the key at the bottom of the screen The first page ...

Page 51: ...parate dots that make up a graph are connected with lines or left as dots This is very seldom of use vs The third option Axes controls whether axes are drawn The fourth Inv Cross controls the appearance of the cursor that is moved by the arrow keys It is best if you try this one yourself to see the effect The fifth option Labels controls whether labels X Y and a scale are put on the axes The only ...

Page 52: ...look at the screen key list at the bottom of the screen you will see only a single entry labeled Press the key under it and your screen will change to look like the middle one of the three right Press it again and the screen will clear completely Once more and you are back to the original appearance Try pressing it a few times to get the feel for its behavior This is what is known as a toggle swit...

Page 53: ...reen but rather to the order that they are defined in the SYMB view If is turned off then the cursor is free to move anywhere on the screen Defn short for Definition You will find that the equation is now listed at the bottom of the screen Press the key labeled The up down arrows will move the cursor from F1 X to F2 X with the definition changing as it does so If is switched off then will not work...

Page 54: ...e current scale For example we can jump to the value x 100 and see the X Y coordinate displayed with the cursor positioned at the far right side of the screen Similarly you could jump to the value x 2 despite this value being inaccessible for the scale chosen since the cursor will normally only move to the values defined by the dots on the screen Calculator Tip The lated values 2 2 Isect to that p...

Page 55: ...e perhaps showing a more interesting section of graph In Out These two options zoom in or out by adjusting the scales by the factor shown The default factor is 4 for both axes but this can be adjusted through the Set Zoom Factor option later in the menu The most useful settings are either 5x5 or 2x2 as these are more likely to preserve nice scales Box commands When you choose this option a message...

Page 56: ...options allow you to zoom in or out by a factor of 4 on either axis The factors can be set using the Set Factors option which gives you access to the view shown above right You will also see a check mark next to an option called Recenter If this is ed then the graph will be redrawn after zooming in or out with the current position of the cursor as its center menu as you can see in the second scree...

Page 57: ...the highlight on Root as shown and press ENTER or Press the then the cursor will jump to the nearest root or x intercept for the function it is on starting its search at the current position of the cursor Try it now Notice the message at the bottom of the screen giving the value of the root that was found To find the other root you need to move the cursor so that it is closer to the other root tha...

Page 58: ...t the value of the x coordinate is stored in the memory If you immediately change to the and hit ENTER then you can retrieve and use this value See The Expert on page 75 for more detail and examples Slope This gives the numerical value of the derivative at the point of the cursor for the current function There are many other methods of doing this some of which can be found on pages 66 70 83 Calcul...

Page 59: ...o choices between F1 X and the x axis or between F1 X and F2 X If we had defined more functions in the SYMB view then this menu would be longer In this case we want the area between F1 X and the x axis so position the highlight as shown and press ENTER The graphs will then reappear with a message requesting that you choose an end point In the screenshot shown right I have pressed and entered the v...

Page 60: ...hoose the boundary as F2 X instead of the x axis so that we will be finding the signed area between curves instead of the signed area under one Again note that the result will be a signed area definite integral not a true area See page 75 for a simple method of finding true areas We now need to choose the end point This time do it by tracing with right arrow to move the cursor As you do the area w...

Page 61: ...the values of the roots as A B C These values can then be used in the calculation to retain full accuracy Extremum The final item in the menu is the Extremum tool This is used to find relative maxima and minima for the graphs is switched on and that the cursor is positioned on the cubic F2 X in the vicinity of the left hand maximum turning point as shown right Press Ensure that and choose Extremum...

Page 62: ...ings o Firstly where is the function most active For what domain on the x axis is it changing rapidly both up and down This is likely to be the domain you are most interested in o Secondly what is the range What sort of values will you need to display on the y axis Change to the PLOT SETUP view and set what you think may be appropriate axes From those you can PLOT and then zoom in or out If the gr...

Page 63: ...d Another possible strategy for graphing which works quite well and perhaps importantly always gives nice scales is to use Enter your graphs into the SYMB view Remember that Auto Scale only works on the first ticked graph Press VIEWS and choose Decimal or press SHIFT CLEAR in the PLOT SETUP view This will give you the default axes probably not showing the graph very well Place the cursor so that i...

Page 64: ...aling with composite functions such as f x 2 or f g x in its SYMB view The and keys are particularly helpful with this x then we can use these in our defining of F3 X F4 X See the screen shot on the left below 1 For example if we define F x x2 1 and F2 x If the highlight is now positioned on each of these in turn and the key pressed then the substitution is performed The result is shown in the rig...

Page 65: ...is sometimes best to leave the evaluation undone 2 For example if F1 X X and F2 X X then 1 2 F3 X F F X will show the correct domain of x 0 for both F2 X and F3 X in the NUM view Pressing will destroy this Using functions in the HOME view Once functions have been defined in the SYMB view of the Function aplet they can be reused in the HOME view and indeed in any other aplet For example suppose you...

Page 66: ... menu One point to remember is that if you use this function in the HOME view you may not receive the result you expect If you try this yourself your result will probably not be the same as that shown right The reason for this is that the result you see is the derivative of x2 x evaluated at whatever value of x happens to be currently in memory This can be seen more clearly if we store a specific ...

Page 67: ...t is much easier and offers the additional advantage of being able to graph the two functions Circular functions There are two issues that influence the graphing of circular functions both related to the scale chosen The first one illustrated on the right causes circles to be ellipses if you don t choose scales for the x and y axes which are square relative to each other The two graphs above are b...

Page 68: ...mple of two images of 2 the same graph x2 9 using two slightly different scales You can see that the second example has y missing pieces 2 Let s look at the circle x2 9 as an example This circle only exists from 3 to 3 on the x axis and is y undefined outside this domain In order to graph it you have to rearrange it into two equations of F1 X 9 X2 for the top half F2 X 9 X2 for the bottom half If ...

Page 69: ...n or out to show the circle This will tend to give nice pixel points If your circle is not centered on the origin then just check tick the box in the Set Zoom Factors box to Recenter That will allow you to turn off move the cursor closer to the point where you d like the centre of screen to be and then Trig functions the graph of a trig function and you are using radian measure then you should cho...

Page 70: ... without moving the cursor and type X then the value it will contain will be the last position of the cursor If you just found a root or an intersection then this will be the value displayed To find the y value for the x coordinate just evaluate F1 X in the HOME view or whatever function you are using o The second way is via the reserved words of Root Extremum Area Slope and Isect Typing any of th...

Page 71: ...m left of the NUM view This can be quite useful as a fast way to reset the scale key pops up the menu on the right The first option of In causes the step size to decrease from 0 1 to 0 025 This is a factor of 4 and is changeable via the NUM SETUP view I find a zoom factor setting of 2 or 5 to be more useful Pressing the The second option of Out causes the opposite effect changing the step size upw...

Page 72: ...reen left shows x 1 dx 3 3333 1 ln2 x followed by e dx 1 0 It may help you to remember the syntax of the differentiation and integration functions if you realize that they are filled in with values in exactly the same way that they are spoken 2 E g x2 1 dx is read as 1 the integral from 1 to 2 of x2 1 dx entered the same way 1 2 X 2 1 X A similar path was taken with the differentiation function so...

Page 73: ...nce of viewing 3 All that is now necessary is to read S1 S1 3 3 as x x 3 3 or as it should be read as x x c 3 If done in the HOME view then S1 must again be used as the variable of integration 2 i e x 1dx is entered as 1 S1 X2 1 X This is shown above together with the results of highlighting the answer and pressing The result may seem odd but is caused by calculator assuming that X itself may be a...

Page 74: ...6 4 5 The final constant of 6 4 comes from substituting zero into the expression and should not be there if we were doing this with the aim of finding an indefinite integral On the other hand we all know that the answer should have a constant of integration so perhaps this extra constant will help you to remember the c Calculator Tip on the hp 39gs if you try to evaluate 2 x x dx able to do it The...

Page 75: ... will see a list of the HOME variables not the APLET button on the keyboard then the display changes to show the variables specific to whatever aplet you are currently using Those shown right are for the Function aplet and the group of Plot FCN variables is shown If you press SK2 labeled tag is currently selected showing as and this means that when you press If you look at the screen shot you will...

Page 76: ...nd the two intersections After finding the first intersection using Intersection we change into the HOME view and store the results into memory variable A We then do the same thing for the second intersection storing the result into B We can now calculate the area in the HOME view using f f2 for 1 the first and f2 f1 for the second Use to duplicate the first integral and edit it to adjust the func...

Page 77: ... X 3 X X 1 Note The AND function can be found on top of the key 2 AND X The reason why this works is that the X 2 and the X 1 expressions are evaluated as being either true which for computers has a value of 1 or false which has a value of 0 By dividing by this domain expression we are effectively dividing by 1 inside the range with no effect or dividing by zero outside the domain making the funct...

Page 78: ...ese numbers that also give nice values if you want to along the graph For example halving each of 6 5 and 6 5 will place the dots 0 05 apart To zoom out instead of in simply double the values producing dots that are 0 2 apart Similarly if you want to center the graph around a particular value then just add that value to the range values The example right is centered around x 1 by adding 1 to 3 25 ...

Page 79: ...of brackets in functions One problem commonly encountered by new users is misinterpretation of brackets The hp calculator will correctly interpret F1 X X2 X 1 as X2 X 1 but will not understand F X X X 1 When used in either Function or Solve it will result in the error message of Invalid User Function Similarly if you want to use the sum to n terms formula for a GP in the Solve aplet and enter it a...

Page 80: ...n indication of whether or not you are on the right track However if you continue to use larger values then the limit appears to change to 1 see right This is obviously not correct so why is it happening The reason for this is that the calculated value of ex very quickly passes the upper limit of the capacity of the calculator which is 10500 When this happens the top and bottom of the fraction bec...

Page 81: ... X The first graph on the right shows the graph of this function for the domain of 0 to 100 The second graph shows how instability develops in the domain 0 to 1E11 1 1011 This apparent instability is caused by the internal rounding of the calculator It works to 16 bits accuracy which means that it can store 12 significant digits for reasons only of interest to programmers This means that when you ...

Page 82: ...lue x 2 1011 the inverted value is so small that 1 1 X becomes exactly 1 and the graph becomes horizontal Of course this is completely the wrong value Although this explanation may be beyond the level of many students it is quite important that they have some understanding of these ideas if they use an hp 39gs to numerically evaluate limits Because of the CAS on the hp 40gs this situation is less ...

Page 83: ...the expression F2 X F1 A X F1 A X in F2 X This is the basic differentiation formula quoted above with X taking the role of h and A being the point of evaluation in this case with A 3 Change to the NUM SETUP view and change the NumType to Build Your Own By entering successively smaller values for X you can now investigate the limit as h tends towards zero In this case it is clear that the limit for...

Page 84: ...tion and store the results into M1 The advantage of this is that you can now view the roots by changing to the Matrix Catalog SHIFT 4 and pressing See page 209 for more detailed information on matrices In addition to this you can access the roots in the HOME view as shown This method works equally well for complex roots See page 309 for details on finding roots of real and complex polynomials usin...

Page 85: ... the others differ in only small ways Aplets downloaded from the Internet however will usually have a radically different VIEWS menus created by the person who wrote the program for the aplet See page 257 for more information on this process if you intend to program the calculator The first image shown right shows the contents of the VIEWS menu for an aplet called Coin Toss which investigates prob...

Page 86: ...The left hand graph is always the active one with results of actions shown on the right We can now use the left graph again to zoom in on another section of interest or alternatively press the key under the label This switches the right hand graph onto the left screen so that you can perform progressive zooms Using or the menu you can then find or examine points of interest Alternatively you can z...

Page 87: ...s shown on the right using an XRng of 8 to 8 Choosing Plot Table gives the result shown left As you can see the scale has been preserved unchanged although without labels The table on the right also uses a sensible scale of 0 25 because of the choice of an x axis scale of 8 to 8 As mentioned choice of scale in the Plot Table view is discussed in detail on page 79 The technique is requires slightly...

Page 88: ...add another graph over the top of an existing one without the screen being blanked first as it usually is As an example if you you may not want to have to wait while all the earlier ones are redrawn F1 X through to F6 X SYMB view then have already graphed functions and then add another one in the If you un the earlier graphs and then use Overlay Plot for the new one then it will be drawn over the ...

Page 89: ... only an ascending section Zooming out would be an option at this stage as would un ing the quadratic in the hopes that Auto Scaling the cubic might give better results The resulting y scale is often not a very nice one Commonly you will find that the y axis appears thick as shown right The reason for this is that the Ytick value is too small resulting in ticks too close together You will usually ...

Page 90: ...as so many factors For example with a zoom factor of 2 zooming out once would mean each pixel was now π 48 while zooming in would give a pixel jump of π 12 The default axes under the Trig option is 2π to 2π If you are primarily interested in the first 2π of the graph then simply change Xmin to zero Alternatively you can move the cursor to π the middle and then zoom in The example right uses zoom f...

Page 91: ...the user to find approximations to the area under a curve by finding either the lower rectangular area the upper rectangular area or the trapezoidal area The user can choose the end points of the interval the type of calculation and the number of rectangles to be used The rectangles are drawn on the screen A worksheet introduces the idea of integration to find areas Linear Programming This aplet v...

Page 92: ... Parametric and press If you wish to ensure that you see the same thing as the examples following then press the button before pressing As with the Function aplet this aplet begins in the SYMB view by allowing you to enter functions but the functions are paired Each function consists of a function in T for X and another for Y Looking at the PLOT SETUP view you will see that we now have to enter a ...

Page 93: ...g is to decide how much of the graph is drawn at all not how much is displayed of the total picture For example gives a graph of As you can see above changing the T range from 0 t 2π to 0 t 5 gives a graph that appears only partially drawn Of course what constitutes fully drawn depends on the function used The value of the parameter TStep controls the jump between successive values of T when evalu...

Page 94: ...tions one should always be careful that the angle measure chosen in is correct The defau t for all aplets is radian measure As usual the NUM view gives a tabular view of the function In this case there are three columns since X1 and Y1 both derive from T As with the Function aplet it is possible to change the starting point and step size of the table and also to change it into a Build Your Own typ...

Page 95: ...tions x1 t A B cos t Bcos A t B 1 1 y t A B sin t Bsin A t B 1 Hint An easy way to vary A and B is to store values to memories A and B in the HOME view and enter the equations exactly as shown New graphs can then be created by changing back to HOME and storing different values to A and B The example shown uses A 4 B 2 5 and has axes set with TRng of 0 to 31 5 step 2 XRng of 21 66 to 21 66 and YRng...

Page 96: ...d in the first 2 seconds only so I ll also restrict TRng to 0 to 2 5 Using Y T T for this TRng means the y values will also range from 0 to 2 5 Maximizing visibility of this range of values is the reason for setting YRng to be 0 5 to 3 in PLOT SETUP The range for the x axis is chosen from the values shown in the NUM view The value of TStep is carefully chosen so that when the motion plots the spee...

Page 97: ... chosen to allow visible motion As the graph appears it can be seen that the ships do not collide even though the final plot may make it appear that they do To find the distance between the two ships at any time t you can enter X 2 X 2 the equation F1 X X1 X 2 Y X X 1 Y 2 into the Function aplet Note that the active variable must be an X in the Function aplet instead of the T of the Parametric apl...

Page 98: ...p regardless of the resulting X and Y positions The values of θRng and for θStep are critical in controlling the appearance of the graph The values set for θRng control how much of the graph is drawn while the values for XRng and YRng only control how much of the graph is displayed on the screen once drawn θStep controls how smooth the graph is as did TStep in the Parametric aplet The default valu...

Page 99: ... 8 n n 1 n 2 As with most aplets the Sequence aplet starts in the SYMB view when you enter formulas The Sequence aplet uses the terminology U N rather than the other commonly used Tn for its definitions in order to avoid having to use subscripts which would not show up well on the screen All functions of this type are assumed to be defined for the positive integers only ie for N 1 2 3 4 Each defin...

Page 100: ... you have begun to enter the sequence definition For example suppose we enter the Fibonacci sequence into U2 by defining U2 N as U2 N 1 U2 N 2 Rather than having to type all of this we can use the buttons provided pressing This is a very convenient feature and worth remembering There is no mark next to the definition yet since the sequence is defined recursively and no values have yet been given f...

Page 101: ... find that the values for those terms of each sequence will appear in the U1 and U2 columns almost immediately In case you didn t realize the reason for the larger text is that the button has been pressed Due to the type of problems one is usually trying to solve with sequences the NUM view rather than the PLOT view is often more useful in this aplet but let s have a look at the PLOT view anyway T...

Page 102: ... U1 in the definition of U2 Once U2 is defined in this way you can change both U1 U2 by simply storing new values into A and R from the HOME view Solving sequence problems Questions like What term is the first to be greater than 10 000 or When does Sn first exceed 10 000 can be answered in the NUM view Simply move into the N column make a guess as to the term you require and type it in The table j...

Page 103: ...when you enter the rule into U1 N All we need do now is switch to the Numeric view to find with some experimenting that U1 46 is the first to exceed one million It is also possible to answer these questions in the Solve aplet For example if we use the Sequence aplet to define U1 N 2 N 1 as before then we can change to the Solve aplet and enter into E1 the equation U1 N 10000 change to the NUM view...

Page 104: ...he loan itself Each quarter the remaining balance is multiplied by 1 0 055 4 and then the repayment of 175 is subtracted You can now follow the progress of the loan in the NUM view with U1 containing time and U2 the amount owing at the start of each time period showing it is repaid during the first quarter of 2023 In reality this type of problem is more easily handled in the Finance aplet see page...

Page 105: ...n and can usually be solved 2 y x 2 v2 u 2ad eg are all equations b a 3 1 c d 2 x 6x 5 0 An expression on the other hand does not contain an sign It can be evaluated or rearranged but not solved When you enter an expression into the Solve aplet it internally puts an 0 onto the end so as to convert it into an equation which can be solved 2 x 4 b 1 eg 1 are all expressions c 2 5 x 6x 2 2 Let s start...

Page 106: ... will depend on what happens to be in the memories V U A and D at the time Pressing SHIFT CLEAR will zero all values Move the highlight to V and enter the value 27 78 then to U and enter 16 67 and finally to D and enter 100 Now move the highlight back to A the value you re trying to find and press the button You should find that you obtain the answer to our problem of 2 47 m s2 process has finishe...

Page 107: ...shown right of 8 57cm The equation is a quadratic in R which means two solutions are possible If you enter an initial estimate of 10 you will obtain the negative solution which is physically invalid in this case Example 2 If f x 3 x 2x2 5x 2 find all values of x for which f x 1 Although you may have a clear picture in your mind and can provide Solve with the estimates it needs I ll assume that lik...

Page 108: ...e page 110 for more information on the effect of the active variable on what you see in the PLOT view Calculator Tip What is worse is that they are reported in The Solve aplet is not able to cope with inequalities Although there is no error message when you use or the answer it supplies is not what you would expect as correct Just don t use inequalities If you have an hp 40gs then you can use the ...

Page 109: ...the normal distribution is UTPN see page 207 which gives the upper tailed probability The syntax is UTPN mean variance value In the Solve aplet set E1 to P UTPN M V X Enter the NUM view press to obtain 201 35cm There are many more ways in which the Solve aplet can be used in conjunction with the functions available in the MATH menu The MATH menu is discussed in detail starting at page 165 with wor...

Page 110: ...lculator substitutes the supplied values in the NUM view into all other variables except B and graphs the left and right sides of the equation as two separate graphs This may not always be obvious because the substitution may produce graphs which aren t visible on the default scale In the graph above you can see from the label on the horizontal axis circled that the active variable is B In this ca...

Page 111: ... restore the variables to the original values this time leaving the highlight on C Since the active variable is now C substitution of all other values means that A B C C 0 5 2 5 B becomes 0 4 In this case both sides are linear and this is shown in the PLOT view Notice that the axis label is now C This would have only one solution and there would be no need to supply any particular starting value I...

Page 112: ... of the messages below These are 2 Extremum it found a minimum but could not reach zero Try solving the equation x 2 4 0 2 and you will see this The smallest value that x 2 can have is 4 at x 2 so the answer 4 0 unless you check supplied will be very close to this such as 2 000000001 or 1 999999999 The problem is that you may not realize that this is not actually a valid solution Bad Guess the ini...

Page 113: ...ct that there is going to be more than one solution to a problem then the PLOT view can help you to obtain estimates 2 x 1 For example x 2 When you plot this you can see that the solutions are near 2 and 1 5 If we now switch to the NUM view we can use these as initial guesses This will give solutions of 2 56 and 1 56 In this case the problem shown will graph easily on the default PLOT view but thi...

Page 114: ...e case of bivariate data for indicating pairing of columns If you have not already done so go to the APLET view highlight When you press and then the Statistics aplet On the screen you will see a key labeled either or Pressing the key under this label changes from univariate to bivariate and back Make sure the key is showing before proceeding If your NUM view had some data in it you could press CL...

Page 115: ...ctually have any data in them then errors will result As you can see in the screens above right the calculator gives not only the standard statistics that any scientific calculator would give but also the minimum and maximum values the median and the upper and lower quartile cutoffs The mode is not given but this is easily obtained from the histogram as we will see later Let s create a second colu...

Page 116: ...her than simply around the columns C1 C2 C0 The reason is that it allows you to easily cope with a frequency table by setting up one column to represent values and another to represent the frequencies If you are not using a frequency table then the frequencies are normally set by default to 1 as can be seen on the previous page So how do we deal with frequency tables Let s set up columns C3 and C4...

Page 117: ...right you will see that when is turned on then information about the graph is given at the bottom of the screen As usual the up down arrows change from graph to graph while the left right arrows move within the graph As an aside pressing the key produces the normal tools of and They all behave in the normal manner as was discussed in detail in the Function aplet chapter The tool can be quite usefu...

Page 118: ...o deal with data displayed in a frequency table but 10 19 14 did not deal with the case where the data was also 20 29 26 grouped into intervals or classes 30 39 37 40 49 23 For example suppose we want to analyze the set of 50 59 17 grouped data in the table on the left As with most calculators the hp 39gs hp 40gs provide only limited methods to deal with data of this form Summary statistics can be...

Page 119: ...he data points 1 2 and 3 Instead the columns extend from 1 2 2 3 and 3 4 This bothers some people and can easily be fixed by changing the HRng If you look at the PLOT SETUP values you will see that they are currently set to 1 to 4 This is the default behavior for Auto Scale To center the columns you need only change the minimum value for HRng by subtracting a half column width giving 0 5 The resul...

Page 120: ...ed not be stored For the teacher this can be a handy way to create sets of data that conform to particular models For 0 03x example if you would like a set of data that conforms to a model of y 2 5e then simply enter any values randomly into C1 and then in HOME perform the calculation 2 5 e 0 03C1 C2 Of course the result will be a set of y values which exactly match the model and this is not desir...

Page 121: ...ng the MATH menu function MAKELIST See the previous page for the syntax of MAKELIST It is also covered in more detail on page 190 Example 1 Simulate 100 observations on a Uniform 0 1 random variable to be stored in C2 In the HOME view type MAKELIST RANDOM X 1 100 1 C2 symbol is one of the screen keys in the HOME view appearing as Note 1 The and read as store 2 The X is simply a dummy variable here...

Page 122: ...he right Its mean turned out to be 2 067 3 decimal places Yours will be different of course after all that s the point of using random numbers Calculator Tip The ly random any more than it is on any command repeatedly on two l lators RANDSEED RANDOM function is not tru computer If you use the RANDOM calculators just out of the box then you wil see the same set of numbers on both calcu This is beca...

Page 123: ...ariate data and we are now going to look at bivariate paired data On the screen in the NUM view of the Statistics aplet you will see a key labeled as either or Pressing the key under this label changes from univariate to bivariate and back Make sure the key is showing before proceeding xi yi 1 5 3 10 8 18 5 13 7 16 3 8 6 15 2 8 7 18 9 22 8 17 5 15 7 14 6 18 8 20 5 12 2 8 0 4 7 17 8 19 If your NUM ...

Page 124: ...e column name Calculator Tip You can enter the xi and yi i e as 1 5 ENTER 3 10 ENTER etc data into both columns simultaneously if you enter it as ordered pairs in brackets Returning to the data from the previous page having entered it into the NUM view we could now use VIEWS and Auto Scale to produce a plot this generally produces very satisfactory results but let s have a look at the PLOT SETUP s...

Page 125: ... curve Although we have not mentioned it in the example so far part of the procedure in dealing with bivariate data is to specify the relationships between columns before plotting This is done via the SYMB view as it is for univariate data The default setting is for the data to be in columns C1 and C2 and because that s where our data is we were able to bypass this process The S1 S2 refer to data ...

Page 126: ...caters for students who have been exposed to exponential equations but not to the extent of e Trigonometric a SIN b X c d Y asin bx c d This model fits a possible trigonometric curve to the data Because the sine curve is periodic the answer will not be unique User Defined discussed on the following page Calculator Tip 1 L in HOME 2 l SYMB m X b display Fit line and press the DEL will have to be re...

Page 127: ...ses is the analysis of time series data Unlike most bivariate data time series values are usually plotted as a line graph i e as connected points This facilitated by Connect For example The sales of an ice cream shop are shown as quarterly sales figures for the years 1992 to 1993 Display this data on a line graph Yr 1992 1993 Qtr 1 2 3 4 1 2 3 4 Sales 12 18 20 15 13 20 23 16 1000 The result with C...

Page 128: ...atistics summary statistics are available through the key in the NUM view Pressing this key changes to a screen which lists the following MEANX ΣX ΣX2 MEANY ΣY ΣY2 ΣXY SCOV PCOV CORR and RELERR See page 131 for information on RelErr yi xi We will use the set of data shown in the table on the left to go through the analysis 2 process a second time and this time 3 examine the line of best fit 2 7 En...

Page 129: ...get the list of the key Make sure that your data set is defined and view before you try to obtain these results Results are only If you now press the key you will see the graph shown right there is no line of best fit on yours press the programmable functions along the bottom of the screen and then press As soon as the line of best fit has been obtained you can switch back to the SYMB view to get ...

Page 130: ...nt that you display the equation in the SYMB view by pressing displays the equation in a form which can be scrolled through the problem with this method is that the calculator thinks that by editing it you are choosing to over ride its choice of equation with your own As long as you press there is no problem but if you press ENTER it changes the FitType from whatever you had previously chosen to U...

Page 131: ...spect of bivariate stats needs to be remembered when the fit chosen is not linear the correlation coefficient is a strictly linear measure of the goodness of fit and this means that the correlation view is always for the linear model even when some other model is chosen There are two methods of dealing with this The first is to use another measure of goodness of fit The second is to linearize the ...

Page 132: ...he correlation is unchanged at 0 9058 even when the new equation clearly fits the data perfectly Checking the The value of RelErr on the other hand has changed from 0 09256 for the linear fit to a value very close to zero for the exponential model rounding error may result in something non zero The alternative to using RelErr is to graph column C1 against ln C2 which also straightens the data Line...

Page 133: ...s With most simpler calculators these values are found by pressing keys rather than reading from a screen so doing a calculation like multiply the mean by 3 5 is not hard The values shown on the screen can also be retrieved for use on the calculator relatively easily For example the set of data below contains a suspected outlier erroneous value In this case one might suspect a missing comma betwee...

Page 134: ...iable name will be pasted into the HOME view for use People often find it easier to simply type them You can obtain the summation sign in MeanΣ by using SHIFT Calculator Tip the NUM HOME The values of the mean and standard deviation retrieved are those of last set calculated If you have more than one set of data in the view then firstly un all except the one you want and secondly press the key in ...

Page 135: ...is is to enter F1 X PREDY X into the Function aplet highlight it and press The equation will be transferred and can then be analyzed using the normal Function tools If you want individual coefficients they can also be obtained from the chosen fit model algebraically For example if the line of best fit is y m X b and the fit line is showing in the SYMB screen as below then the calculations shown ri...

Page 136: ... earlier Algebraically it simply reverses the line of best fit For example the equation Y ˆ would use X Y 1 1662 to predict the X values 0 8199 Whether this is mathematically correct depends on how you interpret the PREDX function If as HP intended you interpret it to mean give me an x value which if used in the PREDY function would give me this y value then it is correct However it should not be ...

Page 137: ...u might be running a Quiz Competition Night or recording times for the 100 meter sprint but in either case it is handy to be able to sort the data into descending order and assign rankings This is easy for small sets of data but becomes difficult for larger sets Competitor Time 12 23 11 47 11 34 12 87 12 23 11 30 10 51 11 34 11 46 12 34 12 23 11 50 12 01 11 97 12 05 12 87 12 02 12 52 11 37 10 75 1...

Page 138: ...umn 3 will produce the rankings for the whole 20 competitors For example competitor number 7 has a time of 10 51 and a rank of 1 Using Stats to find equations from point data eg 1 Find the equation of the quadratic which passes through the points 1 5 3 15 and 5 71 In the Statistics aplet choose mode and enter the data Now change to the SYMB SETUP view and choose the Quadratic data model Clearly th...

Page 139: ...l model for the data Start up the Statistics aplet set it to Either use the VIEWS Auto Scale option or change to the PLOT SETUP view and adjust it so that it will display the data This is not really needed since the line of best fit is what we need and it will be calculated even if the data doesn t show Now change to the PLOT view and press Wait while the line draws Change to the SYMB view move th...

Page 140: ...s having to re type them from the screen Now switch to the Solve aplet and enter the equation to be solved Changing into the NUM view you should find the values of A and K already defined that was why we stored the curve values into the appropriate memories so move the highlight to T and press Result Doubling time is 1 0536 hours Note An alternative to this would be to only retrieve the value of N...

Page 141: ...ew is obtained by importing it from the Statistics aplet The logic is that there is little point in including facilities in the Inference aplet that are already more than ably supplied in the Statistics aplet Hypothesis test T Test 1 µ A company makes boxes of matches which are supposed to contain an average of 50 matches A student has counted the contents of 20 boxes and found the results below U...

Page 142: ...ft The upper normal curve shows the critical range for the t values together with a short vertical line showing the position of the Test T value The lower horizontal line shows the equivalent critical sample mean range The test value for the Student t and the sample mean are also listed in the middle of the screen The regions for rejection of the null hypotheses are shown at the very top of the sc...

Page 143: ...UP view use the import facility as before to import the values from our sample data The default confidence level is 99 so you will need to change that to 0 95 Changing to the NUM view gives the minimum and maximum values for the population mean of 50 16 to 52 44 at a 95 confidence level As before a more visual display can be seen in the PLOT view Thus the sample data indicates in our two examples ...

Page 144: ...6 54 The farmer wishes to know at the 1 test level whether this is statistically significant Our hypotheses are H0 The effects are the same µ µ ie There is no effect from the supplement 1 2 HA Supplement A is better µ µ 1 2 Enter the data into columns C1 and C2 of the Statistics aplet We are dealing with two independent samples in this case and so we need to choose from those tests which involve t...

Page 145: ...ed students which he believes is producing significantly better results He wishes to publish a paper on this and needs to check his results statistically A standardized test is available for which it is known that the normal performance of hearing impaired students at the same stage of study has a mean of 53 6 and a standard deviation of 12 2 When he applies this test to his class of 23 students t...

Page 146: ... rejection marked by the R Change to the NUM SETUP view you can use the import facility to import the summary statistics from the Statistics aplet test and the significance level of 0 05 5 value of 0 05 From the evidence the teacher must reject the alternate hypothesis and conclude that it is not possible to say at the 5 level of significance that his class has averaged significantly higher than t...

Page 147: ... The number of heads is binomially distributed n 4 p 0 5 HA The number of heads is not binomially distributed n 4 p 0 5 Begin by entering the data into the first two columns of the Statistics aplet right We now need to calculate the expected values based on our null hypothesis The expected values are based on the assumption that the results are binomially distributed with n 4 and p 0 5 We can do t...

Page 148: ...probably biased This does not say that it is not binomially distributed just not with those parameters Importing from a frequency table The import facility of the Inference aplet has a small weakness in that it can t import from paired columns defining a frequency table For example suppose we use columns C1 and C2 to define a frequency table ensuring that it is registered in the SYMB view as shown...

Page 149: ...mn This is just to give you something to watch while it works Now change into the Program Catalogue and If you then change to the NUM view you will find that column C0 contains the result You can now import that column s mean and standard deviation into the Inference aplet After you have used the column you will probably also want to delete columns C8 C9 and C0 to save space Bear in mind that if y...

Page 150: ... button rather than using subtract As you do so the solution will be displayed at the bottom of the screen In this case there is a unique solution of x 1 y 2 5 and z 3 E Ex xa am mp pl le e 2 2 Solve the system of equations 3 2x y 5 3 2x y 7 As you may be able to see this is a pair of parallel lines and so has no solution To see this on the calculator we must first change to the 2x2 view meaning 2...

Page 151: ...obvious at first glance this system of equations corresponds to a spindle of planes in 3 space as shown in the diagram above right This situation allows infinite solutions anywhere along the line of intersection of the three planes As you can see right the calculator has correctly indicated the situation 151 ...

Page 152: ... you use is controlled by the button labeled short for rectangular When is selected shown by the dot you are supplying information for a right triangle In both cases the procedure is to supply sufficient information to allow the triangle to be solved hence the message to Fill 3 out of 6 values This request should be taken with a pinch of salt For example in the case of a right triangle it is actua...

Page 153: ...d values are highlighted for convenience 12 cm E Ex xa am mp pl le e 2 2 Find the length of the hypotenuse for the triangle shown right 25 cm Since we don t want the sizes of the angles it doesn t really matter what angle mode the aplet is set to If you worked the previous example then it is probably still in degree mode Press the button to change the screen into the right triangle format as shown...

Page 154: ...e into the SYMB view and ensure that the non right triangle is selected as shown Purely to maintain orientation we will select C as the side that is 10cm long and enter the values shown right Notice that as soon as sufficient information has been entered the message Solution Found appears and the calculator will fill in the missing values The additional button label of Press will appear to announc...

Page 155: ...ee the initial view shown right When you Pressing SYMB NUM or PLOT will make no difference to this aplet as it is quite limited and only has the one view consisting of two related pages Parameters There are a number of parameters or variables which must be either supplied or solved for These are N The total number of compounding payments or payments Mode This has the value of Beg inning or End dep...

Page 156: ...ow to plan your setup of the aplet Ordinary compound interest Invest 1000 into a bank account paying 6 5 per annum for 5 years Interest is calculated monthly and credited to the account at the end of each month What is the investment worth at the end of the period Looked at from the point of view of the person investing the money the cash flow is initially outwards negative by 1000 The final payme...

Page 157: ...last for 20 years The value of N is 240 representing 20 years of monthly payments On this basis the monthly annuity can be 4289 71 Loan calculations You wish to purchase a car by taking out a loan The current interest rate is 6 5 and you can afford to make monthly payments of 300 You want to take out the loan over a period of 6 years and to still owe 10 000 at the end of that period you expect an ...

Page 158: ...ization screen The initial appearance is as shown As can be seen the default number of payments to amortize over is 12 Press the Pressing the button will amortized the loan over the first year As can be seen right 2 369 77 has been paid off the principal leaving a balance of 17 630 23 Of the payments made 1 230 23 went towards the payment of interest button will transfer the balance back to the pr...

Page 159: ... it may be necessary to press the screen key to go back to the opening view The first choice made by the user should be the The default level is that of Y a X h 2 v which allows the student to change all parameters at once By having the student choose the levels of Y aX2 Y x h 2 or Y X2 v the teacher can confine the study to the effects of only one coefficient at a time if desired The default stat...

Page 160: ...e v coefficient is high lighted and can be changed using the and keys The size of the changes to h and v is controlled by the key and the same range of values is available for the values of a as in mode You can move from one coefficient to the next by using the and keys As with the mode the equation in y ax2 bx c form its roots and its discriminant are shown on the right half of the screen The and...

Page 161: ...d displayed An incorrect answer is shown as an animated graph on the screen when you press flashing repeatedly between the required graph and your incorrect guess This has to be seen to be appreciated a screen shot can t do it justice If your guess and the required graph can t be shown on the same screen then this animation may not be possible If you are unable to find the answer pressing will dis...

Page 162: ...ght Like the Quadratic Explorer this aplet has only one screen rather than the usual PLOT SYMB and NUM views If the aplet has been used before then it may be necessary to press the screen key to go back to the opening view shown When the student presses The or key can be used to toggle between the y sin curve and the y cos curve The or key can be used to toggle between radian measure and degree me...

Page 163: ...e location of the control point when control is set to the graph translates left and right the c coefficient or up down the d coefficient when control is set to the graph dilates parallel to the y axis the a coefficient or parallel to the x axis the b coefficient Unlike the SYMB mode where the b coefficient goes up or down in steps of 0 1 the increments in PLOT mode are not regular but are chosen ...

Page 164: ...s are restricted to a given range and only certain values within that range This is done to make the aplet more efficient and faster The range of values is shown below Coefficient Range a 3 to 3 in steps of 0 1 b 0 3 to 5 in steps of 0 1 c 4π to 4π in steps of or whatever is set by d 3 to 3 in steps of 0 1 6 π If you go to Hewlett Packard s website you can download a worksheet for use with your cl...

Page 165: ...rammers It contains the names of various environment variables allowing easy pasting into programs Generally it is easier to simply type them The PHYS menu this physical constants menu contains the values of many of the physical constants required by students in physics and chemistry The CAS menu this menu contains those commands which are only available on the hp 40gs and are associated with the ...

Page 166: ...w keys or the key corresponding to the first letter of the function Pressing the right arrow key again will move down the functions a page at a time In this case since every single function in the Polynomial group begins with a P and there is only one page of them there is no difference between the methods Move the highlight down to POLYFORM and then press the ENTER key Your HOME view should now l...

Page 167: ...e enough to trigger your memory One piece of terminology that will be used in this section of the manual is argument The arguments of a function are the pieces of information it is expecting you to feed it before it will give you an answer These might be numbers variable names lists matrices or algebraic expressions The calculator will not guess what you mean If you don t feed it the information i...

Page 168: ...f a proton mp me ratio fine structure constant magnetic flux constant Faraday constant Rydberg constant Bohr radius Bohr magneton constant Nuclear magneton const Photon wavelength Photon frequency Compton wavelength formulae Chemistry Avogadro s number Boltzmann s constant Molar volume Universal gas constant Standard temperature Standard pressure Physics Stephan Boltzmann constant Speed of light m...

Page 169: ...pulate complex numbers Constants e i and various others Of more use in programming Convert contains a list of functions allowing conversion of units Hyperb the hyperbolic trig functions List allows manipulation creation of lists of numbers including stats data Loop iterative functions Matrix a rich collection of functions to manipulate matrices Polynom another rich collection this time to manipula...

Page 170: ...This function converts degrees to radians Eg DEG RAD 30 0 5235 DEG RAD 180 3 1415926 RAD HMS DEG HMS See also FLOOR num This function is the same as the CEILING function except that it always rounds down Eg FLOOR 3 75 3 FLOOR 45 01 45 Note FLOOR 2 56 3 not 2 The FLOOR function is the same as the mathematical function greatest integer which is studied in many mathematical courses If you want to gra...

Page 171: ...it with an initial guess If there is only one answer then any guess will do but if more than one solution is possible then more care needs to be taken with your guess to ensure that it is in the neighborhood of your desired solution 3x 5 Eg a Solve x2 0 Use FNROOT X2 3X 5 X 2 d 3d 5 b Solve 1 3 4 Use FNROOT D 3 5 3D 4 1 D 0 As with Solve if your expression involves more than one variable then what...

Page 172: ... can also be used to deal with time E g What time will it be 1 hr 34 min and 15 sec after 3 min past 6 pm Type HMS 18 03 HMS 1 3415 Ans 37 min 15 sec past 7 pm see right See also HMS RAD DEG DEG RAD HMS num This function works in the same way as the HMS function but in the opposite direction It converts decimal degrees or time to degrees or hours minutes and seconds The format of the returned answ...

Page 173: ...tion It would be used with the XPON function which returns the power part of the number in scientific notation Eg Change 487 23 into scientific notation to get 4 8723 102 MANT 487 23 4 8723 XPON 487 23 2 4 Change 0 0005087 into scientific notation to get 5 087 10 MANT 0 0005087 5 087 XPON 0 0005087 4 See also XPON MAX num1 num2 This function returns the larger of two values entered This is not nee...

Page 174: ...ction gives you the remainder when one number is divided by another It is considered to be an mathematical operator in the same way that a plus minus times or divide sign is Because of this it does not need its arguments placed in brackets as most of the other functions in the MATH menu do Eg 43 5 48 43 MOD 5 3 35 MOD 7 0 14 MOD 5 1 function num1 num2 To find x of y use the function X Y Eg 10 of 4...

Page 175: ...5 95 that normally sells for 6 50 What is the discount as a percentage of the usual price Use CHANGE 6 50 5 95 See also TOTAL TOTAL num1 num2 To find out what percentage X is of Y use the function TOTAL Y X Note the reversed order Eg What percentage is a score of 53 out of 81 on a test Use TOTAL 81 53 What percentage is 124 of 112 Use TOTAL 112 124 See also CHANGE RAD DEG radian_measure This funct...

Page 176: ...nt figures s f To do this simply put a negative sign on the second argument Round 32345 to the nearest thousand Use ROUND 32345 2 32000 Round 3405 63475 to 6 s f Use ROUND 3405 63475 6 3405 63 See also INT FLOOR CEILING TRUNCATE FRAC SIGN num Another function designed more for programmers returning a value of 1 0 or 1 depending on whether the number supplied is positive zero or negative Eg SIGN 45...

Page 177: ...entific notation of the number you feed it It would be used with the XPON function which returns the power part of the number when in scientific notation Eg Change 487 23 into scientific notation to get 4 8723 102 MANT 487 23 4 8723 XPON 487 23 2 4 Change 0 0005087 into scientific notation to get 5 087 10 MANT 0 0005087 5 087 XPON 0 0005087 4 This function could be of use to you if you are just le...

Page 178: ...has been graphed in the PLOT view and that the FIT screen key has been used to plot the line of best fit for the pair of columns If these conditions are satisfied then the function PREDY 3 5 will produce a predicted y dependent value for the x indep value of 3 5 Calculator Tip The line of best fit used in the function PREDY is whichever one was last plotted It is up to you to ensure that this is i...

Page 179: ...ill rearrange a formula so that its subject is another variable To do this the formula must be rewritten so that it is an expression which equals zero The ISOLATE function then rearranges the formula in terms of that variable Eg 1 Rewrite the formula d 1 at2 in t 2 Firstly rewrite as d 1 at2 0 2 Use ISOLATE D AT2 2 T 2D The result needs interpretation as the answer should be T Firstly the T is mis...

Page 180: ...wn right The main use for this is going to be when a programmer does not know in advance what function the user is going to type in QUAD expression var name b2 4ac b to give both This function uses the quadratic formula x 2a roots of a quadratic using the S1 formal variable to represent the symbol The quadratic is entered as an expression and you must indicate which variable is being solved for si...

Page 181: ... in single quotes For example X 2 4 F1 X woul QUOTE X 2 4 d serve the same purpose as F1 X On the other hand entering F1 X will not work but F1 QUOTE X will No one ever promised consistency See Example 1 on page 262 in the chapter Programming on the hp 39gs hp 40gs for an example of use in writing code The function written as expression var1 value var2 value This is called the where function The r...

Page 182: ...es the results T Th he e T Tr ri ig go on no om me et tr ri ic c H Hy yp pe er rb bo ol li ic c g gr ro ou up ps s o of f f fu un nc ct ti io on ns s These two groups of functions cover the Trigonometry functions plus others which are less commonly used and which have consequently not been given their own keys on the face of the calculator Use them in the same way as the normal SIN COS and TAN fun...

Page 183: ...nother function giving greater accuracy than the one it replaces This greater accuracy would probably never be required in a school setting EXPM1 num This function is designed to be more accurate when anti logging very small values close to zero It gives the x value not of ex but of e 1 EXPM1 exp minus 1 You may wonder how this is an advantage since you must then add 1 to obtain the correct answer...

Page 184: ...en integrated with respect to the variable specified Any other variables in the expression will be regarded as constants with values taken from the current memory values Symbolic integration can be done in two ways Firstly by replacing one of the limits of integration with a symbolic variable S1 S1 S5 Secondly and more conveniently by doing it in the Function aplet see pages 59 to 75 var_name expr...

Page 185: ...on the right shows the calculator deriving the Taylor polynomial for sin x up to the 7th power The SIN X function can be approximated by taking terms from the polynomial 3 5 7 x x x sin x x 3 5 7 1 7 1 x3 1 x5 x x 6 120 5040 In this example the result is shown twice The first is calculated with MODES set to Standard the second highlighting it and pressing with MODES set to Fraction 4 The second sc...

Page 186: ...y retains the original in case you need to it later for re use The exception is when you enter a complex number in polar form using the angle sign on the keyboard above the button When you do this the calculator converts into the two other common forms of rcis format and a b format as shown right In the example right the lowest line shows how the number was been entered The first two lines show ho...

Page 187: ...very useful with complex numbers and so is also covered here If given a vector complex number a b SIGN will return another vector complex number which is a unit vector in the direction of a b Note again the requirement for doubled brackets a b i e SIGN A B returns 2 2 a b2 a b2 y This is very useful not just in complex numbers but also in vector problems 6 See also SIGN in the Real group IM RE ARG...

Page 188: ... complex number supplied See also CONJ ARG RE Note As mentioned earlier a very useful function can be found on the keyboard as the SHIFT function for If you enter a complex number in r form as shown right then the calculator will display it in the form r cos θ r sin θ from and as an a b ordered pair Note the r cos θ r sin θ form is used only when in radian mode If in degree mode then it returns on...

Page 189: ...A key pressing SHIFT first to get lowercase T Th he e C Co on nv ve er rt t g gr ro ou up p o of f f fu un nc ct ti io on ns s This is a set of functions which allow conversion of metric units to imperial and vice versa The list is not very extensive but does cover the more common ones The syntax is the same for all For example the ÆC function converts to Celsius from the equivalent Fahrenheit To ...

Page 190: ...ist The resulting list has a length one less than the original Eg L1 1 4 7 10 13 LIST L1 3 3 3 3 MAKELIST expression var_name num num num This function produces a list of the length specified using a rule of your choice It is very useful not only in programming but in statistical simulations and modeling The syntax is MAKELIST expression variable name start end increment where expression is the ma...

Page 191: ...10 1 will return a list of 1 s and 0 s corresponding to the simulated Bernoulli trials Various examples of this process are given in the Expert User section which immediately follows the chapter on Univariate Statistics on page 121 πLIST list This function returns the product of all the elements of a list LIST 2 3 5 would return a value of 30 Eg POS list num This function conducts a search of a li...

Page 192: ...eventually run the program If the object is a matrix then the return value is a two element list as rows columns ΣLIST list This function returns the sum of all the elements of a list Eg LIST 2 3 5 would return a value of 10 REVERSE list This function reverses the order of elements in a list Eg REVERSE 2 4 1 7 10 would return 10 7 1 4 2 SORT list This function returns a list that is sorted into as...

Page 193: ...a supplied initial value for a specified number of iterations Each iteration uses the answer to the previous evaluation as the value for the variable in the next evaluation Eg ITERATE X2 1 X 2 5 gives an answer of 15745023 This answer is obtained as follows initial value X 2 first iteration using supplied x2 1 3 initial value of 2 new value X 3 second iteration 2 1 x 8 new value X 8 third iteratio...

Page 194: ...lculating the results of summation notation problems The syntax of the function is ordered in the same way as one reads a summation expression see the examples below 5 2 2 2 Eg 1 i which expands to 12 2 32 4 52 giving an answer of 55 i 1 can be evaluated using I 1 5 I2 6 Eg 2 xi where x1 2 x2 10 x3 13 x4 11 x 20 x 2 5 6 i 1 can be evaluated by first defining a list L1 as 2 10 13 11 20 2 and then c...

Page 195: ...ing with Matrices on page 209 COLNORM matrix Finds the column norm of a matrix the maximum over all columns contained in the matrix of the absolute values of the sum of the elements in each column 1 2 3 Eg For the matrix M1 4 5 6 the column with the largest absolute sum of 13 is column 3 1 5 4 COND matrix Finds the condition number the 1 norm column norm of a square matrix CROSS vector vector This...

Page 196: ...example 4 EIGENVAL matrix This function returns the Eigenvalues in vector form for a matrix The values can be complex as shown right EIGENVV matrix This function returns the Eigenvectors and Eigenvalues for a square matrix It returns a list variable consisting of two arrays a matrix containing the eigenvectors and a complex vector containing the eigenvalues IDENTMAT size This function creates an n...

Page 197: ...t then evaluate DET matrix first record the fraction and then evaluate DET matrix INVERSE matrix to obtain usually a non fractional matrix i e A 2 3 1 1 5 3 4 5 A 2 4 2 Remember that the inverse matrix is not just the matrix but the fraction times the matrix See also RREF DET LQ matrix This function takes an mxn matrix factors it and returns a list containing three matrices which are in order an m...

Page 198: ...sed mainly by programmers to manufacture a matrix with dimensions rows columns using the supplied expression to calculate each element Eg MAKEMAT 0 3 3 returns a 3 3 zero matrix Note If the expression contains the variables I and J then the calculation for each element substitutes the current row number for I and the current column number for J during the calculation 2 3 4 Eg MAKEMAT I J 3 3 retur...

Page 199: ...uced row echelon form with the final column containing the solution 2 3 14 x y z Eg The system of equations 2x y z 3 4 2 2 14 x y z 1 2 3 14 is written as the augmented matrix 2 1 1 3 4 2 2 14 which is then stored as a 3x4 real matrix M1 We now use the function RREF to change this to reduced row echelon form and store it as M2 This gives the final result shown in the matrix M2 on the right giving ...

Page 200: ...atrix is real then the result is orthogonal upper quasi triangular If matrix is complex then the result is unitary upper triangular SIZE list or SIZE matrix This function returns the size of the list or matrix specified Since normal users would probably know anyway and could find out easily via the list catalog this is clearly another of those functions which are of more use to programmers who won...

Page 201: ... matrix This function returns a vector containing the singular values of the supplied matrix TRACE matrix This function finds the trace of a square matrix The trace is equal to the sum of the diagonal elements or the sum of the eigenvalues TRN matrix This function returns the transpose of an n x m matrix 2 3 For example if M1 1 2 then TRN M1 would return 2 1 0 3 2 4 0 4 201 ...

Page 202: ...ets The function f x above has roots 2 3 and 1 The screen shot below shows POLYCOEF correctly giving the coefficients as 1 0 7 and 6 for a final polynomial of f x 7x x3 6 POLYEVAL coeff1 coeff2 value This function evaluates a polynomial with specified coefficients at the point specified The coefficients must be in square brackets followed by x3 7x the value of x not in brackets ie f x 6 has value ...

Page 203: ...e scrolled right and left to see the missing terms 4 Eg 2 Expand 3a 2b This function contains two variables A and B which must be expanded separately The first expansion treating A as the variable is done using the expression POLYFORM 3A 2B 4 A As you can see if you examine the view after pressing the expansion of the expression in terms of A has been done but the terms involving B are not fully e...

Page 204: ... be input as a vector in square brackets x 2 x 3 x 1 x3 7x 6 we can enter the coefficients as Eg Using our earlier function of f x 1 0 7 6 As you can see in the screen shot the roots of 2 3 and 1 have been correctly found See page 309 for details on finding roots of real and complex polynomials using the CAS on the hp 40gs 204 ...

Page 205: ...n is to save time Rather than using the MATH menu for every entry of the COMB function you can enter it once and then it repeatedly changing the parameters each time 2 For large values of N 150 or so it is important to use the COMB function rather than using N N R R because the massive values involved in calculating the factorials will cause inaccuracies internally The COMB function has internal m...

Page 206: ...a normal die RANDSEED number It is important to realize that the values produced by the RANDOM command are not truly random numbers Inside the calculator is a mathematical procedure an algorithm which uses a seed number to produce them Unfortunately when taken straight out of the box two calculators will produce exactly the same sequence of random numbers This can be a problem For example a class ...

Page 207: ...t of 1 87m and a standard deviation of 10 4cm 2m x 1 87m σ 0 104m 2 σ 0 010816 Ans P height 2m 0 1056 Eg 2 The population of Year 12 Applicable Mathematics students had a mean exam score of 65 and a standard deviation of 14 What two scores will cut off the top and bottom 10 of students 0 1 0 1 65 i e Find x0 such that P x x0 0 1 Using the Solve aplet right we can reverse the normal direction of th...

Page 208: ...reversing the normal positions of then the probability given will be the lower tailed The reason for this lies in the symmetry properties of the normal curve UTPC degrees value This is the Upper Tailed Chi Squared probability function It returns the probability that a χ2 distribution with the supplied number of degrees of freedom is greater than the value supplied See page 147 for an example of th...

Page 209: ...at vectors The key pops up the menu shown on the right replacing the highlighted matrix with any empty one of the new type that you specify Press SHIFT CLEAR to delete all Matrices like most other objects on the calculator can be sent to and received from a computer or another calculator using the and keys On the hp 40gs this is done using the two cables supplied one being a mini USB for use with ...

Page 210: ...ld now look like the screen shot right If you now press the down arrow key on the keyboard the highlight will move back to the first element in the second row Enter the numbers 4 5 and 6 and you will find that the calculator automatically drops down to row three without the need to use the down arrow key again since it now knows how many columns the matrix is to contain Finish your matrix so that ...

Page 211: ...rther worked examples involving matrices in the section at the back of the book x y z 2 3 6 x y z Eg 1 Solve the system of equations 3 12 3 4 13 x y z 2 3 1 6 x y 12 Solution The system of equations can be 1 3 1 represented as the system of z 13 3 1 4 matrices 1 2 3 1 6 x y z 12 1 3 1 and this system can then be algebraically rearranged to 3 1 4 13 2 3 1 1 where the inverse matrix is 1 3 1 3 1 4 2...

Page 212: ...nd method is that it does not make it clear that the operation is really left multiplication by the inverse rather than division an operation which is not strictly speaking defined for matrices but is allowed for convenience on the calculator The third option is actually identical to the first The original hp 38g only had the INVERSE function and the x 1 function was added in later models They are...

Page 213: ...not the best way to display the answer The fact that the determinant is incorporated into the inverse makes whole numbers unlikely 1 A better way is often to write the answer as a fraction multiplied det A by a matrix of whole numbers If we multiply the inverse by the determinant then we can usually remove the fractions i e with M2 being 13 17 1 Thus we can finally write A 1 7 5 6 2 6 10 1 An alte...

Page 214: ...culator the functions DOT and ABS give the dot product and magnitude respectively when fed with vectors The calculator writes vectors as row matrices For example a 3 4 would be written as 3 4 The calculations are shown in the two screen shots on the right Remember to change into degree mode first The list of matrix functions available through the MATH menu is covered starting on page 195 Not all f...

Page 215: ...t in the second list Many of the normal mathematical functions also work on lists of numbers by performing the operation on each individual element Lists on the calculator can contain more than simply numbers For example the return value for some matrix functions is a list where each element is a matrix Elements of a list can be matrices lists and many other things The column variables C1 C2 C9 C0...

Page 216: ...position shown then a zero is inserted before the 4 with all the elements below shifted down one position You can then type your new number Having entered the editing screen you may be wondering how to exit since no key is apparently provided for this Simply press SHIFT LIST again to return to the catalog level or press HOME if you ve finished altogether Changing of individual elements of a list c...

Page 217: ...re is a Notepad Catalog containing independent notes which is available via a NOTEPAD found above zero In the explanations below an instruction to press NOTEPAD will always refer to the Notepad Catalog not to the aplet Note The average user will probably not use the aplet Note Notes attached to aplets are explained in the chapter Using Copying Creating Aplets on page 226 so only a brief example is...

Page 218: ...le don t read notes or explanations so it is debatable how much use they are anyway Some aplets also have sketches attached to them but this consumes approximately 1Kb of memory per sketch and so was not common on earlier models which only had 23Kb of RAM memory and so didn t have a lot to spare On the hp 39gs hp 40gs as programmers become used to having plenty of memory to use aplets have become ...

Page 219: ...test or examination It is wrong and could result in severe penalties Some institutions require a complete reset before any examination See page 42 on how to do this Notes can be shared between students in the same way as can be done for aplets lists matrices and programs It is worth pointing out that this will not help you in a test situation since on the hp 39gs the strength of the infra red link...

Page 220: ...u to begin typing in your Note Before we begin a word about making your typing easier The normal method to enter an alphabetical character is to use the ALPHA key Lowercase letters are obtained by pressing SHIFT first The ALPHA key can be held down with one hand obtained via while you type with the other but this isn t convenient and lowercase can t be locked this way Space can be ALPHA SPACE with...

Page 221: ... Syntax error The third is an oddity If you choose the superscripted 3 then you will find that the character which actually appears is that of the inverse operator 1 This character is available on the keyboard above the divide button The reason for this odd transposition is based in the history of the calculator The original hp 38g only had the function INVERSE and the 1 operator was added for con...

Page 222: ...very primitive when you try to do anything at all complex This is not meant as a criticism of the calculator It does an extremely good job at what it was designed for working with numbers but it was never designed to compete with a computer drawing package When you first enter the Sketch page on your calculator you will see the view at the top right There are four screen keys available The key all...

Page 223: ...to a computer drawing or painting program The small cursor cross in the middle of the screen can be moved around using the arrow keys If you press the screen key labeled then a trail will be drawn as you move the cursor Notice the small dot next to the showing that it is engaged key turns the cursor into an eraser and automatically disengages Pressing the as well Pressing the same key again diseng...

Page 224: ... Once you have chosen a GROB in which to store the screen capture you will need to specify the corners of the rectangle to be captured Position the cursor on one corner and press Move to the diagonally opposite corner and press again Once an image is captured it is possible to paste the captured screen portion into the a Sketch page using the VAR key The screen does not have to be blank but to mak...

Page 225: ...een menu showing make sure it is set up that way before you proceed When ready press and hold down the ON key then press the PLOT key and release both The screen will be automatically stored into GROB G0 You can then paste it into a sketch rather than from the options at the bottom of the screen Move the highlight to Graphic and then into the right hand column and find G0 Press the key and then pr...

Page 226: ...er with the ability to transfer them to another calculator via cable hp 40gs or infra red hp 39gs Generally this will involve making small modifications to the standard aplets and saving them under a new name In a chapter which follows we will cover the use of software on a PC to do this As well as this you can download additional aplets and programs written by people who do enjoy programming Thes...

Page 227: ...was designed infra red communication was not considered desirable and a mini serial cable connection is used instead This cable shown above right connects two hp 40gs calculators via their mini serial ports It is an HP proprietary cable which can only be purchased from HP or an HP reseller Both cables are supplied with the hp 40gs calculator as standard equipment but the hp 39gs is supplied standa...

Page 228: ...bout 3 4cm It is best not to put them extremely close together or touching because in that position a small misalignment will cause most of the signal to be lost Placing them 3 4cm apart allows the beam to spread and compensates for any slight misalignment When you press you will see the menu shown right The option you need for an hp 39gs is HP39 IrDA which transmits via the infra red link On the ...

Page 229: ...n transmitting aplets or notes then this means that the connection was lost and the transmission The two most common causes of this are mis alignment of the two calculators The infra red beams must be correct y lined up and within 8 10 cm low batteries In my experience the transmission process begins to act up a little before the low battery indicator icon appears at the top of the screen When rep...

Page 230: ...ndard aplets as you wish The only limit is the calculator s memory Depending on what you put in them the calculator s memory is normally sufficient to store anything from 30 to 100 aplets Let s look at each of the two scenarios in turn In the first case what the student needs to do is to make a copy of the Function aplet to hold his homework the functions he had already set up and then do the unex...

Page 231: ...say Related Sets If desired you can the original Statistics aplet afterwards ready for next use This saved aplet can now be downloaded to all the students calculators using the infra red link in the case of an hp 39gs or using the cable in the case of the hp 40gs This ensures that each student has exactly the required data sets with PLOT views pre set to the teacher s needs An ambitious teacher mi...

Page 232: ...ments of your particular course the aplet and enter the formulas shown below Firstly E1 V N N R R P R 1 P N R E2 V J A B N N J J P J 1 P N J E3 P e M M K K E4 P J A B e M M J J E5 P A B K X 3 2 X X E6 P e K A e K B E7 P UTPN M S2 X E8 P 1 UTPN M S2 X E9 P UTPN M S2 A UTPN M S2 B E0 P UTPN M S2 M K UTPN M S2 M K These formulas can be used in the NUM view to solve problems involving the probability ...

Page 233: ...s important not to use a Normal approximation then replace the N N R R portion with COMB N R The COMB function has special facilities for handling large numbers This will not help greatly with the iteration time needed Equations E3 and E4 These two equations can be used for calculations involving individual and cumulative Poisson probabilities where M is the mean The technique is otherwise identic...

Page 234: ...wo placing equations 1 to 4 into an aplet called Discrete PDFs and the others into another called Cont PDFs I encourage my students to do this because it reinforces the correct technique of first of identifying whether the problem is discrete or continuous The Transformer aplet This aplet is based on the Parametric aplet and allows students to investigate geometric transformations using 2x2 matric...

Page 235: ...level of ability For an able class you might choose to give no more guidance than to suggest that they confine their investigations initially to placing numbers only on the diagonals It may be a good idea to challenge them to record their matrices on the board as they discovered them For a less able class you might hand out a list of matrices they should investigate Perhaps in the form of a set of...

Page 236: ...es that is highly symmetrical like a square as it makes it harder to recognize transformations Calculator Tip It is probably faster to have the class set it up themselves instead of sending it via cable or infra red Plus if the class is not to regard this as magic then it helps if they understand how the aplet works This is best accomplished by having them set it up themselves You might even consi...

Page 237: ... day month after month without expecting to experience problems The PC s operating system may be quite stable but any system that complex needs to be completely shut down and restarted at least once a week or once a fortnight The same is true of the hp 39gs and hp 40gs Its operating system is of course not as complex as that of a PC but despite this if you continue to use it without shutting it do...

Page 238: ...ors have used a USB connection The HP Connectivity Kit called HPGComm is the software used for the older serial port models Because it is only of use to these earlier models it will not be discussed here Information on using this software can be found in a variety of places such as the author s website at http www hphomeview com Although it will transfer information notes aplets and programs to an...

Page 239: ... the electronics for use in infra red communications S Se en nd di in ng g f fr ro om m c ca al lc cu ul la at to or r t to o P PC C Any aplet note program matrix or list can be copied from a calculator to a PC using the supplied mini USB cable A sketch can be transferred by copying the aplet to which it belongs The key to this ability is the screen key labeled and its companion key This is shown ...

Page 240: ... re starting it with the calculator already turned on Sometimes it can take up to 10 seconds for the connection to stabilize iii The batteries may not be sufficiently fresh Communication with the PC uses a lot of power and problems may occur with low battery power even before the Low Battery Indicator appears above the screen on the calculator You should also be aware that even supposedly new batt...

Page 241: ... this menu are HP39 IrDA infra red communication from hp 39gs to hp 39gs This option only appears on the menu for an hp 39gs HP39 40 USB not used at present This option would allow cable communication from calculator to calculator via a double ended mini USB cable However no such cable is currently part of the equipment supplied HP39 40 Ser Used for cable communication from calculator to calculato...

Page 242: ...lso show various pop up boxes to show progress Their contents depends on what is being transmitted The filename that is used on the PC to store the object is normally contracted as shown in the screen to the right This is not important since thanks to those two small files mentioned in the previous paragraph the full name will be recorded and restored when transferred back to the calculator The re...

Page 243: ... since the calculator knows they belong with the aplet and will automatically transmit them with it This can greatly increase the transmission time and it is important that you don t interrupt the process early If you want to see these helper programs press SHIFT PROGRAM to see a list of the programs currently on your calculator Even if there are no other programs currently stored you will always ...

Page 244: ...gain choose the USB Disk drive option from the menu The Connectivity software will respond with a list of objects contained in the folder you selected If you only want to download one of them then just highlight it and press ENTER To download multiple objects use the button to select them Calculator Tip The displayed list will contain only objects that are appropriate for the current view of the c...

Page 245: ... learn for yourself The Quadratic and Trig Explorer aplets now built into the chip were once teaching aplets which had to be downloaded from the web Each successive model adds another one or two new aplets to those which are standard Finding aplets The Hewlett Packard site is one possible starting point and can be found at http www hp com calculators From that point you can follow the links to col...

Page 246: ...with a page which may be similar to the one on the previous page It may contain either programs or aplets or both Generally you will be able to click on a link that lets you download that aplet as a compressed ZIP file A ZIP file is a special type of file which contains one or more files in compressed The reason for the compression is simply to allow you to download them from the Internet as one s...

Page 247: ...m For example a teacher might choose to set up a structure containing directories for each of the courses being run with further directories containing all the aplets which were relevant to that course Again it must be stressed that each aplet must be in a separate folder Having downloaded an aplet from the web to the computer we now have the task of transferring it from the computer to the calcul...

Page 248: ...ss flexible in its operation To download an aplet you should be in the APLET view when you press the button To download a program you should be in the PROGRAM CATALOG The menu will only display things that are appropriate for that view aplets in the APLET view programs in the PROGRAM CATALOG If all goes well you should find that you presented with a menu which lists the aplet or program you are tr...

Page 249: ... the curve using Lower rect Calculator Tip If there is documentation with an aplet then you should read it It often contains information which is needed for the efficient use of the aplet It may also have one or more student worksheets which can be copied and used in a classroom Most of these programmed aplets have helper programs that are automatically loaded into the Program Catalog When you del...

Page 250: ...og and remove them Even with 230Kb to play with it is advisable to do this or your memory will gradually be used up As an example of this look at the aplet called Coin Tossing shown in the APLET view right Looking at the list of programs shown in the Program Catalog view you will see a set of programs which all begin with the letters COIN The convention encouraged by Hewlett Packard is to name the...

Page 251: ... still holding it down pressing and releasing the 1 key then ON When you do the image appears on the computer Once the image is captured it can be copied to the clipboard and pasted into another application The software also allows it to be saved as a BMP image file All the images of calculator screens in this book were captured in this way Capturing into the Sketch view A variation of this captur...

Page 252: ... The average user tends to be a student who is most interested in creating and editing Notes that he she can take into assessments Consequently in this small chapter we will look only at using it to edit Notes and cover programming elsewhere If your Note already exists on the calculator then the obvious first step is to transfer it from the calculator to the PC This is covered in detail on page 23...

Page 253: ...ady existed It is also possible to create Notes on the PC from scratch to make a copy of an existing Note or to delete a Note The key to this is the set of buttons at the bottom left of the screen The first button labeled Create Note in Folder will create an empty Note with the title New Note You can change that title by typing in the field titled Note Name In the example shown to the left the nam...

Page 254: ...g Note with the title Copy of You can then change the title in the normal manner to anything desired Calculator Tip length If the name is more than 12 l For as Principles o The Connectivity software will allow you to enter a Note title of any In practice this will not work characters long then the calcu ator will truncate it in the display example Principles of Conductivity will appear in the Note...

Page 255: ...aplets The key to the entire process of creating completely new aplets is the VIEWS menu and its controlling command function SETVIEWS This function allows you to override the normal behavior of an aplet and superimpose new properties by linking in a set of programs written by you This is the single most important point in the process and should be kept in mind It is mildly deceptive to call these...

Page 256: ...uld consider using the software discussed later as it makes the process far easier To use this software you must be able to send to and receive from a computer and for models before the hp 39gs hp 40gs this means buying a cable For the hp 39gs hp 40gs the mini USB cable required is included in the package with the calculator In this chapter we will begin by creating our first two aplets entirely o...

Page 257: ...ble to have sub menus in the VIEWS menu by having your option call a program which then pops up another menu of options This is usually shown by an placing an ellipsis after the VIEWS option such as the one below right of Graphs An example of the VIEWS menu from an aplet is shown right The aplet is called Time Series and is designed to analyze time series data When designing this menu the author h...

Page 258: ...ons listed right In this case the menu has far fewer options because the operation of the aplet is very simple The reason for the Start option is discussed on page 261 On the right is the VIEWS menu for an aplet called Curve Areas which finds the areas under curves using various approximations and is used to introduce the definite integral Because it deals with functions and graphs its parent is t...

Page 259: ...on aplet 5 Symbolic Setup 16 Views menu item 2 Plot Table if the parent is the Function aplet 6 Numeric Setup 17 Views menu item 3 Overlay Plot if parent is the Function aplet 7 Views menu 18 Views menu item 4 Auto Scale if parent is the Function aplet 8 Aplet Note view 19 Views menu item 5 Decimal if the parent is the Function aplet 9 Aplet Sketch view 20 Views menu item 6 Integer if the parent i...

Page 260: ...sary to include this program since once it has done its job it would normally never need to be run again but it is usually kept and transmitted with the aplet so that an expert user could modify it if they wanted to An entry which consists of empty double quotes allows you to access commands which appear on the parent aplet s normal VIEWS menu Since your menu has replaced this normal menu they wou...

Page 261: ...ariables to pre set angle modes or axes so that the aplet runs smoothly You should always bear in mind that the user may make changes to any axes you set or store their own values into variables as part of some other calculation not realising that you ve used them as part of your aplet The results can be very unfortunate if you don t bear this in mind Another important reason for including a Start...

Page 262: ...normal SYMB view but for the Message aplet instead of the Function aplet The title appears at the top of the screen as usual Press SHIFT PROGRAM to view the Program Catalog Press to create a new program and call it MSG SV see right with part of the new program typed in Into this empty program type the following code obtaining the quotes from the CHARS view When you finish typing just press SHIFT P...

Page 263: ...ew language of 20 You could use the PROMPT for a key to be pressed command instead but INPUT is more flexible MSG FN MSG S MSG SV Puts an initial message up The SETVIEWS command is discussed in detail on the previous pages This is the most complex of the programs See right for an explanation The command GROB in the program left stands for Graphic Object and creates a GROB from the F1 X expression ...

Page 264: ...d that your new menu appears Press to exit Providing that you have done everything correctly this is now the end of the process the aplet is now ready to be run In the APLET view make sure the highlight is still on the aplet and press or ENTER to run it If you get an error message at any time then you may have to and the program When you do this the aplet will run the program MSG S which will disp...

Page 265: ...dow is still displaying in the background To stop this happening you could have included in MSG IN a line of ERASE which is a command to erase the display screen Try editing the program inserting this line before the MSGBOX line and running it again The option of Message 2 displays the same message as we saw before but presented in a different way The DISP command divides the display screen up int...

Page 266: ... to graph this function by setting 1 the post execution view number to 1 the PLOT view then you would need to include the command CHECK in order to it or it would not graph You may wish to edit the MSG SV and MSG FN program to try this The next lines display the expression using the four options available The line GROB G1 F1 QUOTE X 0 converts the expression F1 X into a Graphic Object GROB The num...

Page 267: ...e re sized in the PLOT SETUP view The box on the other hand would change size if the screen size were to be changed in PLOT SETUP The FREEZE command is needed to ensure that your screen is visible to the user and not immediately replaced by the next view FREEZE resumes execution of the program as soon as any button is pressed Note that SETVIEWS has a Start option and also a final option consisting...

Page 268: ...ram changes the value of Xmin and then changes it back In the original version the user had to press PLOT to force a re draw This technique fools the calculator into thinking that the PLOT view has changed and therefore forces a re draw without the need to press a key It also re multiplies the matrices in case the user has changed one by hand instead of going through the VIEWS menu This program se...

Page 269: ... columns is then extracted and used to reset the value of Tmax The new image matrix is also recalculated Note The indenting used is not required and is there simply to make the program easier to read The amount of memory take up by a few extra spaces is minimal but well worth it in terms of readability This program puts up a message instructing the user and then allows them to edit the transformat...

Page 270: ...en to re create the same Transformer aplet used in example 2 This second example will allow us to concentrate fully on how to use the The Connectivity Kit rather than the programming task since the programming has been discussed in great detail earlier Example program Log X base b This is a small program that will find the log of any number to any base using the change of base law Clearly this is ...

Page 271: ...ent allows you to put a title a prompt and a more detailed explanation on the screen to help the user see what is The result is shown using the command which divides the screen up into seven d be to use another statement such as MSGBOX Log of X to the base B is ROUND LOG X LOG B N This is followed by a succession of INPUT statements to obtain the value the base and the required accuracy Notice the...

Page 272: ...ing code to each view as we go If you are not sure what the Views menu is then you should go back and read the information starting on page 255 before proceeding This is done using the portion of the screen shown to the right As was explained on page 259 the SETVIEWS command works using triplets of information and this screen simply automates this process For each entry you supply a View Name the ...

Page 273: ...he Edit View Program button on the far left is enabled Clicking on this changes the focus from the Aplets tag to the Program tag allowing you to enter the code for the program You should practice this process now by re creating the Transformer aplet which was used as Example 2 on page 268 You will find the code listed on the pages following 268 Please note that if you open the folder in which you ...

Page 274: ...he Function aplet As with the previous example begin by creating a directory to hold the aplet and then run The Connectivity Kit Select it in the directory window so that any files crated will be saved there Create an aplet with a parent base aplet of Function in the same way as the previous example If desired you can add text to the aplet s Note view see page 217 in order to give the user instruc...

Page 275: ...you have done this correctly then your VIEWS menu have three entries shown right when it is transferred to the calculator The text for the helper programs associated with each menu entry is shown below 275 ...

Page 276: ...e of this particular entry is the fact that the Exit View was set to 7 the VIEWS menu This means that when the user presses in the first thing they will see after this code executes is the VIEWS menu The variable G is being used here as a flag A flag is a programming term for a variable that is used to tell whether or not some task has been done or some setting has been set correctly Often the fla...

Page 277: ...se different axes The flag value of G is then set to 1 so that the next program can tell that the axes are ready to use The function is also re entered in case the user has changed the SYMB view Users have an annoying habit of changing things so try to allow for this in your programs by making them fool proof The next program below runs when the user chooses the second menu option of Explore and i...

Page 278: ...that this section of code only runs if something has been plotted If you run the program and then later change to the SKETCH view you will be able to see this stored image Finally the user is presented with two messages which tell them what to do The next section contains the code which performs the work in the aplet by setting up a loop which repeats until the user presses the ENTER key to termin...

Page 279: ...s have problems with objects plotted off the screen particularly if they start on the screen and end off the edge The HP does not and this simplifies your programming task considerably at times Finally the line itself is drawn Even though part of the line extends off the screen there is no problem the excess is clipped by the calculator The next section of code below waits until the user presses a...

Page 280: ...line add a new variable D to allow the size of the increment to change Set an initial value of D of 0 5 at the same point as the values of M and C Then change the lines in the CASE stataement so that D is added subtracted instead of 0 5 Add two more IFs to the CASE statement so that if they press the increment doubles and if then it halves You will also need to add another message box line telling...

Page 281: ...ge The speed issues and the lack of string handling mean that programs such as games are not easy to create Some programmers choose to work instead in an alternative language called sRPL For those who have some programming background this is an assembly code language If you re not sure what this means then basically it means working at a language level where you are writing commands that are execu...

Page 282: ...the abilities of the calculator itself it s graphing facilities it s built in functions and so on Essentially you are operating on a bare chip and having to create everything yourself It is possible to access some of these via back door methods but they are not simple In addition the HPG CC language itself provides some of these abilities such as writing to the screen and these abilities are being...

Page 283: ... programmers on those models or taking those models into account when developing new features This is basically due to lack of interest from programmers the developers can t really be expected to continue to support a model that no one s programming on I myself have written a few small programs in it but just didn t have the time to learn it fully If the language becomes popular on the new models ...

Page 284: ...ll contain a small amount of traditional ROM that can t be altered but this contains little more than information the calculator needs on how to reboot itself and how to load a new operating system into the flash ROM when it becomes available Any updates to the calculator s ROM can always be found on HP s website at http www hp com calculators and information on them will also be found at the auth...

Page 285: ... concern to educators may be whether an hp 39gs user can load the operating system of an hp 40gs and thereby gain access to a CAS This is not possible because the hp 39gs has less flash ROM installed than the hp 40gs The operating system of an hp 40gs is quite a bit larger than that of the hp 39gs due to the inclusion of the CAS It will not fit onto the ROM chip of an hp 39gs and any attempt to tr...

Page 286: ...remove a check next to the equation whose number is given by n An interesting bug is actually quite useful if you UNCHECK 0 then all equations are unchecked instead of only equation 0 Unfortunately the same is not true for the CHECK command As they say in the trade It s not a bug it s a feature SELECT name This is used to set the active aplet if necessary If the name has spaces in it then it must ...

Page 287: ... only worth it if you have more than two or three nested IFs Note that colons are not required for the ENDs which terminate the internal IF clauses IFFERR statements THEN statements ELSE statements END This can be used to error trap programs where there is a possibility of something going wrong which would normally crash the program such as evaluating a function at a point for which it is undefine...

Page 288: ...ce memory use by placing the code in a separate program and calling it from different locations See the SETVIEWS command for information on how to link a program to an aplet when it does not appear on the primary menu Note that if the name has spaces in it then it must be enclosed in quotes STOP This command can be used to abort execution of a program Control resumes in the HOME view 288 ...

Page 289: ...x2 y2 as the corners The coordinates are relative to the settings in the PLOT SETUP view ERASE This command erases the current display screen FREEZE This command halts execution until the user presses any key Execution resumes on the next line of the program LINE x1 y1 x2 y2 This draws a line on the screen using x1 y1 and x2 y2 as the ends The coordinates are relative to the current axis settings ...

Page 290: ...et unset value of all pixels This means that it can be used to erase previously drawn lines If you would like to see this command in action download the aplet called Sine Define from the author s website The HP HOME view at http www hphomeview com This aplet contains extensive use of this command 290 ...

Page 291: ...register as an error but all sort of strange things happen DO statements UNTIL test clause END This loop executes the statements within it until the test clause evaluates as true It must execute at least once because the test is not done until the end of the loop The example right checks for a positive integer from the INPUT statement To be even more user friendly you could let the user know what ...

Page 292: ...tement cannot be replaced by one of the loops or conditional branches available in the HP Basic language T Th he e M Ma at tr ri ix x c co om mm ma an nd ds s EDITMAT matrix var key at the bottom When the user presses execution resumes after the EDITMAT statement This command pops up a window in which the user can edit or input a matrix with an REDIM matrix var size This command is very useful if ...

Page 293: ... the commands will not operate with the hp 40gs There may be a brief display of the communications symbol a small arrow in the top right corner of the display but there will be no other result PRDISPLAY If you place this command in a program then the current display will be sent to the infra red printer PRHISTORY This command whether issued in the HOME view or in a program will send the entire con...

Page 294: ...ight in the rounded box sets up the scale of C major The code which then follows plays the first two bars of the tune Strangers in the Night In this header the duration of a note T is set to 0 5 seconds It is easy to change the tempo of the music by adjusting this In this case you may find that the music sounds a little better with T set to 0 55 or 0 6 seconds T is a crotchet T 2 a quaver etc CHOO...

Page 295: ...own below right if the axes are set to the default values of 6 5 to 6 5 and 3 1 to 3 2 The xpos and ypos values refer to the top left corner of the text when displayed The clipping rules are a bit complicated probably due to the fact that the command was done in a bit of a hurry in a hotel room late one night in Chicago after I d pleaded with the programmers If the xpos ypos corner is off the top ...

Page 296: ...nstead of continuing in the background N before the first use of the the variable Using the PROMPT INPUT variable title prompt message default value This command puts up an input view which can be used to obtain responses from the user The degree of control over appearance is quite If you want the default value to be whatever the user last input then use INPUT N N instead If you do this then you s...

Page 297: ...WAIT duration This command pauses execution for the specified number of seconds Execution resumes at the next statement after the WAIT command 297 ...

Page 298: ...ight advantage that the answer is given in the same form that you would see it if you used the Quadratic formula Just This method is shown right using the the result edit and square the decimal part to find the value of the discriminant if you need the result in surd format The S1 is the calculator s version of the sign Just the result and remove the S1 to obtain the positive solution replacing th...

Page 299: ... 0 1 7321 is just that portion and square it The S1 means The only real advantage of this method is that it gives the answer in the same format as the quadratic formula and this may be of use 3i but if you don t recognize it then Method 2 Using POLYROOT An alternative method is to use the POLYROOT function and store the results to a matrix This offers the advantage of being able to examine the res...

Page 300: ... in the MATH menu in the Polynom group See page 204 for more information The results show that the x intercepts are 1 0 2 0 and 3 0 The y intercept is found by evaluating F1 0 in the HOME view giving the point 0 6 Step 3 Switching to the PLOT view via VIEWS Decimal you will find that the function does not display as well as it could Since it is the y axis that is not displaying enough we will use ...

Page 301: ...rdinate of the second turning point into memory B as shown Now use the Step 5 The PLOT view shows that part of the area we require for part iv is negative so we need to know the x intercept between the two turning points Fortunately we know from Step 2 that it is the point 2 0 If we did not know this already then we could use the menu again retrieving this time from the VAR menu the variable calle...

Page 302: ...tch to the PLOT view and use the Intersection tool to find the point of intersection It is worth noting that although the point of intersection is on the screen here this is not necessary The Intersection tool will work even if neither line is visible on the currently set axes Method 2 Using a matrix 3 x 2x y 7 2 3 7 Step 1 Rewrite x y 2 as 1 4 2 4 y x 2 3 1 7 This means that y 1 4 2 Step 2 Switch...

Page 303: ...able from the internet called the Simult 3x3 aplet It allows easy solution of 2x2 and 3x3 systems of linear equations in a format which is more user friendly than the use of matrices for student who are not familiar with them The disadvantage is that it shows no working Note If your simultaneous linear equations have algebraic coefficients then you will not be able to use any of the above methods ...

Page 304: ... 3 Result 16x 4 96x 216x 2 216x 81 ii Use POLYFORM 3A 2B 5 B to expand the polynomial as a function of B Then use the polynomial function again ing the result from the first expansion and expanding this time as a function of A The key can then be used to view it using the left and right arrows to scroll the screen left and right 4 3 2 2 3 5 Result 243a 5 810a b 1080a b 720a b 240ab 4 32b 304 ...

Page 305: ...ours iii How long does it take for the number of colonies to double i Find N and k using the calculator 0 Step 1 Start up the Statistics aplet set it to and enter the data given Change to the SYMB SETUP view and specify an Exponential line of best fit for the data Step 2 Press VIEWS and choose Auto Scale If the line shown does not appear then press and then Wait while the line draws Step 3 Change ...

Page 306: ...esult 268 269 colonies 1 iii Find t so that N N0 2 Step 1 Find the values of N0 and k and store N into memory A 0 and k into memory K so that it is un necessary to re type them See page 135 for instructions on finding the parameters from the exponential fit curve Step 2 Switch to the Solve aplet and enter the equation to be solved Changing into the NUM view you should find the values of A and K al...

Page 307: ... and M2 respectively Finally use the HOME view to calculate the answer using the function IDENMAT 2 to produce a 2x2 identity matrix and making sure to store the result into M3 In this case the result is a horrible decimal The fractional equivalent can be found by setting the MODES view to Decimal 6 and then re evaluating as shown right From this it can be seen that the common denominator seems to...

Page 308: ... roots are integers so there is no need to store it into a matrix Coefficients must be in square brackets separated by commas iii The method is to solve the complex polynomial z5 32 0 setting the other coefficients to zeros This is shown in the second POLYROOT calculation in the screen shot right In this case the results are unlikely to be integers so we store them into M1 The result is shown belo...

Page 309: ...e configuration menu shown right In the configuration screen move the highlight to the Num factor option shown right and press to set it Then press to quit from the configuration menu and return to the main screen Now press ENTER to tell the calculator to execute the SOLVEVX command The calculator will then ask if you want to turn Complex Mode on Tell it The final result is shown right Pressing VI...

Page 310: ...m assuming that the collision will occur in the first 6 seconds and in the axes range chosen This can always be adjusted if my guess is wrong The reason for choosing 15 on the YRng is to ensure that the x axis is visible on the screen Notice in the second screen that Simult must be checked if the plot is to be a good illustration of the ship s movements If you ve done this correctly then you will ...

Page 311: ...first step is to graph the particle s path We go into the Parametric aplet and enter the rule into the first equation X1 Y1 After setting TRng to 0 to 6 and then using VIEWS Auto Scale we get a result which is does not look like a circle but this may be due to distortion through not using a square screen If we inspect the PLOT SETUP view we can see that the settings are nearly double those of the ...

Page 312: ...heses being tested are H0 There is no relationship between grades awarded and years at school They are independent HA There is a relationship Year Grade awarded A B Total 8 25 15 40 If H0 is true then the expected frequencies should be those in the table on the right 9 10 Total 25 25 75 15 15 45 40 40 120 Enter the observed and expected frequencies into columns C1 and C2 of the Statistics aplet In...

Page 313: ...2 contingency table the number of degrees of freedom are 2 2 To find the critical χ0 05 value we enter values of 2 for D the degrees of freedom and 0 05 for P the probability and then move the highlight to V the value and press As it turns out the required critical value is 5 99 and so we would accept the null hypothesis and conclude no relationship 313 ...

Page 314: ...your students calculators Into this aplet enter the functions shown and set the axes as shown The choice of x axis here means that each pixel will be 0 02 apart which means that when students trace the cursor along the graph they will obtain nice values This aplet can now be sent to each student s calculator at the end of a lesson using the infra red link Accompanying questions should address the ...

Page 315: ... to un F1 X and then to zoom in repeatedly on X 2 in the PLOT view in an effort to find the hole They won t of course but you can enjoy watching them and then discuss why they didn t perhaps a good way to introduce the idea of limits However there is a trick to this If you use the default axes of 6 5 to 6 5 then there will be a hole see right because X 2 falls on a pixel point and so because it is...

Page 316: ... on why f x same as f x 1 2 2 1 for x 0 iii Composite functions can easily be defined as can be seen in the examples to the right In the first screen shot F1 X X2 X and F2 X F1 X 3 have been entered into the SYMB view The second substituted view is obtained by moving the highlight to F2 X and pressing the button If desirable you can further simplify using POLYFORM With the highlight on F2 X press ...

Page 317: ...essively smaller values for X in the NUM view since X is taking the role of h in the expression lim f a h f a f a h 0 h To investigate the gradient at a different point change back to the HOME view enter a new value into A and then return to the NUM view The disadvantage of the previous method is that it is not very visual As mentioned before an alternative is to use the Chords aplet In this aplet...

Page 318: ...n in the SYMB SETUP view and then use the curve fitting facilities to find an equation 3 2 2 Curves of the form y mx b y ax bx c y ax bx cx d and y axb can be fitted using the d xn Statistics aplet and this should be enough for the students to deduce the rule n xn 1 for themselves It dx is advisable to ensure that the students are familiar with the process of using the Statistics aplet to find equ...

Page 319: ...uld be very tedious and the aplet automates the process so as not to obscure the learning O Op pt ti im mi iz za at ti io on n A method which I find to be efficient in introducing the idea of optimization is via the maximization of the volume of an open topped box If we start with a sheet of card which is 15cm by 11cm then we can form a box by removing squares from the corners and folding up the s...

Page 320: ...find quite difficult to come to grips with is that of sketching a field of slopes from a derivative function and from this sketching a family of curves An aplet from The HP HOME View web site at http www hphomeview com called Slope Fields will assist with this process In this aplet the user enters the derivative function into F1 X and then uses the VIEWS menu to produce a field of slopes A cross h...

Page 321: ...ced by using the Parametric aplet to graphically illustrate the motion of a particle If this is set up properly then it can be a very helpful teaching aid as the graph will slow down and speed up as it appears illustrating the velocity and acceleration of the particle See page 96 for a fully worked example of how the Parametric aplet can be used to produce motion graphs of the form shown right The...

Page 322: ...vide very flexible tools for the investigation of sequences These can easily be adapted to investigate series as well Information and worked examples of using the calculator for evaluation of sequences and series can be found in the chapter The Expert Sequences Series on page 102 One of the common errors that students make when using the Solve aplet with GPs is to try to solve for solutions which ...

Page 323: ... also work with piecewise defined functions which are often the type that are used in examination questions There are also two aplets which can aid greatly in this process called Quad Explorer and Trig Explorer and are built into the calculator Both of these aplets allow the student to explore the effect of changing parameters on the shape of the graph one using a quadratic and the other with the ...

Page 324: ...vantage of the calculating power of the hp 40g or hp 40gs It can be found at Hewlett Packard s web site http www hp com calculators or on the Help page of The HP HOME view http www hphomeview com What is a CAS Although you may not have thought about it consciously you are probably aware that most calculators do not operate with algebra in the same way that a human does Generally speaking solutions...

Page 325: ...ly correct answer and it does it by following the same rules that you do The HP CAS system was created by Bernard Parisse Université de Grenoble for the HP 49g calculator It was improved and adapted for inclusion on the HP 40g with the help of Renée De Graeve Jean Yves Avenard and Jean Tavenas and again adapted for inclusion in the HP49g HP48GII and HP 40gs calculators The HP CAS system offers the...

Page 326: ...t it was an hp 40g and thus activate the CAS This caused immense problems in educational markets that required that calculators must not have a CAS and consequently the hp 39g was released in 2004 It was an upgraded model of the hp 39g the differences being vastly greater speed a new Finance aplet and most importantly a chip from which the CAS had been totally removed In 2006 the new models the hp...

Page 327: ...cesses is not the same screen as that shown above To ensure that the CAS is in default mode enter the CAS and press SHIFT MODES Now press SHIFT CLEAR This will restore default settings The current variable By default the current variable is X and this is the variable that is entered when you press the button on the keyboard There are certain functions such as SOVLEVX which assume that you are solv...

Page 328: ...menu Entering and editing an expression When entering an expression the main point to remember is that evaluations and appending of operations are always done to the currently highlighted element This is most easily seen with an example A more detailed explanation will then follow of how the CAS editing screen operates when entering and editing expressions The task we will be performing in this fi...

Page 329: ...hown to the right Press the again to evaluate the highlighted expression v Press If your CAS is in its default configuration then the result will simply be a return of the expression x 2 20 The reason for this is that the default setting is to only factorize over the set of real numbers This needs to be altered using the CAS configuration menu vi To change the CAS configuration press SHIFT MODES a...

Page 330: ... typed the 3 Press up arrow twice Then press ENTER Notice that pressing up arrow caused more and more of the expression to be highlighted Pressing ENTER evaluated the currently highlighted expression of 3 4 to be 81 Press left arrow once then down arrow once Press 3 then press up arrow three times finally press 2 DO NOT use the X2 button for this Notice that in each case the power was applied to t...

Page 331: ...es P and Q added below node A You may notice that it is heavily canted to the left and this tends to be fairly typical of the way we generally write expressions Now press up arrow three times and then divide by 5 The three up arrows moved the highlight up to node A high lighting the entire expression Dividing by 5 therefore applies to the entire expression with the result shown below 81 X A B E C ...

Page 332: ...pear Node Q will then become an addition with two new nodes below Finally exit the CAS by pressing HOME Note There can be a problem with the way that the X2 button is handled If you try going back through the same exercise but pressing the X2 button at step 3 F you will find that this makes it impossible to access and edit the power because the X2 operation is stored differently This is purely a p...

Page 333: ...n then either press ON to exit or use for the final character If the character you echo is inappropriate for the situation in the CAS view then it may be rejected Using the CHARS view is not the most convenient method and some commonly used characters are provided via special keyboard shortcuts These are SHIFT 0 inserts The button also has a special function in the CAS If you SHIFT 1 inserts i SHI...

Page 334: ...ve the selection immediately to the bottom left corner of the branch of the editing tree currently being worked on This is best seen by experimentation effectively if a number of terms are currently selected the selection jumps to the single term at the bottom of that branch ii SHIFT Pressing SHIFT will move the selection to the top of the tree effectively selecting the entire contents of the CAS ...

Page 335: ...the wrong level and are having trouble removing it then you can highlight and edit an expression in line as if you were entering it in the calculator s normal HOME view For example highlight part of an expression as shown right Now press SK1 and choose Edit expr from the menu You can now perform any editing you require and the result will be inserted into the full expression at that point Cursor m...

Page 336: ...ted is the one furthest right in the currently highlighted section For example if the highlight was as shown in the screen above then the current focus would be on node B in the tree shown right Successively pressing DEL would begin at node E deleting first the node s 81 X A B E C D 2 3 G Q P 5 R 2 S contents then the operation multiply which connected it to the tree Try it and see This process is...

Page 337: ... behavior to the normal HOME History If you press SYMB while in the CAS then you will see something similar to the view on the right with all previous calculations and results recorded if the memory is not to be gradually used up Alternatively you can access the Memory Manager see page 30 and clear the CAS History there As with the normal History it is worth deleting the contents regularly by pres...

Page 338: ...w and then storing it into F1 X or whichever is desired as shown right The reverse process is also possible using PUSH but it is more limited in that you must use the symbolic variable S1 When you then press you will find that seemingly there has been no result However when you access the CAS History by pressing SYMB you will find that the expression has been added to the tail of the History and c...

Page 339: ... it See page 342 Evaluating algebraic expressions When an expression is highlighted pressing ENTER will cause it to be algebraically evaluated and any functions to be applied accordingly For example if you highlight 2x 3 3 as shown right then pressing ENTER will give the result shown Further examples are shown below In each case it is only the highlighted expression which is evaluated Depending on...

Page 340: ... below even though it still does not add the c see page 73 for reasons Calculator Tip 40 and pressing will not scroll it VIEWS button then 48 digits of it 200 The result of the example above extends off the edge of the screen If you press the you will find that it can now be scrolled and the entire value seen all The amazing abilities of the CAS are such that even the entire results of something l...

Page 341: ...IFT 2 3 SHIFT 1 12 13 At this point the screen should appear as shown above right ii We will now simplify selectively in order to be able to record working beginning with the denominator ENTER iii Because the entire denominator is selected pressing will now select the numerator To evaluate this press ENTER again iv Now press SHIFT to select the entire expression and then ENTER to evaluate it v To ...

Page 342: ...SHIFT 72 SHIFT 75 ii Now simplify each surd in turn assuming working is desired ENTER ENTER ENTER and press ENTER to simplify iii Finally select the entire expression with SHIFT iv If you want the result as a decimal press NUM Pressing SHIFT NUM will cause the calculator to analyze the decimal and re instate the surd 342 ...

Page 343: ...2x 35 i Find lim x 7 x 7 The sequence of keys for this is scroll to lim and press ENTER 2 35 7 7 ENTER 1 ii Find lim x 2 x 2 The sequence of keys for this is scroll to lim then ENTER 1 2 MATH scroll to QUOTE ENTER 2 0 SHIFT ENTER ENTER Some notes 1 The limit approached from above would be entered as QUOTE 2 0 2 The use of the QUOTE function forces the CAS to treat the 2 0 as an algebraic entity ra...

Page 344: ...x 2 iii Find lim x x 2 5 Limits to infinity are also permitted using the lim function with infinity entered using the shortcut SHIFT 0 scroll to lim and press ENTER ENTER 344 ...

Page 345: ...o the command in the HOME screen Factorization Press until the entire polynomial is highlighted or press SHIFT While the required expression is highlighted fetch the COLLECT function from the menu ENTER ENTER Note Firstly remember that the extent of the highlight plays a very important role Only the highlighted section of the polynomial will be included in the COLLECT brackets This allows partial ...

Page 346: ...ration menu will allow you to find the other two imaginary solutions as shown right Example 6 Solving simultaneous equations x y 3 Solve the following system of equations x y 1 In the CAS enter LINSOLVE X Y 3 AND X Y 1 X AND Y Note that when entering the two equations you must highlight the first one before pressing AND obtained via SHIFT If you don t do this then the CAS will assume that the AND ...

Page 347: ... The command is LINSOLVE 2 X K Y 1 AND Q 3 X Y 5 X AND Y and it produces the results shown Press VIEWS to see the final solution in a scrollable format Note that KY above must be entered as K Y using or the CAS will interpret KY as the name of a variable In the CAS variables can have more than one letter as is discussed on page 328 347 ...

Page 348: ...ession in terms of a and b As can be seen above the initial integration gives an equation involving a fraction This can be simplified by multiplying both sides by 6 highlighting the entire equation first Notice that when the final simplification is equal to zero the calculator does not bother to include the 0 All expressions are assumed to be equal to zero unless otherwise specified 2 The second p...

Page 349: ...to remove the AND then do it properly The other equation is still available from the CAS History Begin by ensuring that no part of the current equation is highlighted and that the cursor is positioned where you want the new equation immediately after the AND If any portion of the expression in the editor is highlighted when you perform an then it will be replaced by the expression being echoed To ...

Page 350: ... SHIFT 2 2 1 ENTER The CAS will then echo the function back to you and if you press VARS to go to the VARS view you will find that it is now a defined variable Use the button at the bottom of the screen to see the definition of the variable Press ON to exit the view Although we used X as our variable here there is no reason for this We could just as easily have defined it as f K 22K 1 You can now ...

Page 351: ...eturns a value of 0 false indicating that it is not a prime number Using the FACTOR function from the menu shows that its factors are 641 and 6700417 Note The ISPRIME function gives correct results for integers up to 14 10 Beyond that level the results are highly probable to be correct but not guaranteed They are obtained using Rabin s Algorithm and are called pseudo primes 351 ...

Page 352: ...ENTER ALPHA Z SHIFT SHIFT ex SHIFT i SHIFT ALPHA t SHIFT ENTER Note The reason for pressing within the menu is to jump to the first function starting with an S the letter on the key Pressing it again jumps to the next function starting with S which is SUBST iii Next we linearize it ENTER ENTER ENTER Note 1 As in the previous case the is used to jump to the first function that starts with an L the ...

Page 353: ...be equivalent to the expression shown right Note that the screen image above is in small font purely to allow the entire expression to be seen Your screen will not be unless you ve selected small font earlier v We now separate the real and imaginary parts of M into separate functions storing them as X1 t and Y1 t ALPHA M MATH 9 ENTER ENTER ENTER SHIFT ALPHA X 1 SHIFT ALPHA T The parameter order mu...

Page 354: ...splay X1 t X1 t and evaluate each side The is not used to solve anything but just to display both at once for comparison so that it can be seen whether or not they are equal as required To aid in this we will change to the small l SHIFT ALPHA CLEAR ALPHA X 1 SHIFT ALPHA T SHIFT T SHIFT ENTER We now font c earing the screen first ALPHA X 1 SHIFT ALPHA As can be seen the two are algebraically equiva...

Page 355: ...nction def tion will be purged as soon as you perform any operation that uses the current variable On the screen define an expression X1 T i Y T which can be sent to the aplet evaluating it 1 and changing back to large font too SHIFT SHIFT ALPHA CLEAR ALPHA X 1 ALPHA T SHIFT 1 ALPHA Y 1 ALPHA T SHIFT ENTER Now store to the aplet using the PLOT button on the keyboard choosing X1 Y1 in the Parametri...

Page 356: ...unction as if you had typed it in yourself Pressing PLOT at this point will produce the screen shown right The symmetry we predicted earlier is now visible This may not be the best possible view and you may wish to use PLOT SETUP to change this π ix The final step is to accurately evaluate f To do this return to the CAS and enter the following 3 ALPHA X 1 SHIFT 3 3 SHIFT ALPHA Y 1 SHIFT 3 3 SHIFT ...

Page 357: ...ill VIEWS d1Y X is Pressing will display the screen shown right Press to paste the example into the CAS editing screen The screen shot right has been obtained by pressing and cutting and pasting in a Paint program to obtain a wider result The reference to LDEC at the bottom of the screen Pressing jump to the screen for LDEC used to represent the first derivative Highlighting this and pressing ENTE...

Page 358: ...here are others that you can access via the MATH button or the SHIFT CMDS menu The screen menu functions are listed in their categories below Algb Diff Rewri Solv Trig COLLECT DERIV DISTRIB DESOLVE ACOS2S DEF DERVX EPSX0 ISOLATE ASIN2C EXPAND DIVPC EXPLN LDEC ASIN2T FACTOR FOURIER EXP2POW LINSOLVE ATAN2S PARTFAC IBP FDISTRIB SOLVE HALFTAN QUOTE STORE INVX lim LNCOLLECT POWEXPAND SOLVEVX SINCOS TAN...

Page 359: ... work in the CAS or are replaced by different versions The functions available in the MATH menu in the CAS are as follows Algebra Complex Constant Diff Int Hyperb Integer Modular COLLECT i e DERIV ACOSH DIVIS ADDTMOD DEF ABS i DERVX ASINH EULER DIVMOD EXPAND FACTOR ARG CONJ π DIVPC FOURIER ATANH COSH FACTOR GCD EXPANDMOD FACTORMOD PARTFRAC DROITE IBP SINH IDIV2 GCDMOD QUOTE STORE SUBST IM RE SIGN ...

Page 360: ...r only in that menu They are ABCUX DIV2MOD IABCUV LAP PLOTADD SERIES STURMAB CHINREM EXP2HYP IBERNOULLI LIMIT PSI SEVAL TSIMP CYCLOTOMIC GAMMA ICHINREM PA2B2 Psi SIGMA VER DIV2 HORNER ILAP PLOT REORDER SIGMAVX The abilities of the functions listed here and on the previous page will not be discussed in this text beyond the examples given on the previous pages The manual supplied with your calculato...

Page 361: ...ing with N useful summary An example is always given and pressing currently highlighted in the editing screen The help screen can be a little crowded as you can see to the right but generally contains an extremely will cause this example to be pasted into the editing screen replacing whatever is There will usually be up to three cross references to other functions Pressing or will take you to the ...

Page 362: ...Now press SHIFT CLEAR This will restore default settings Configuration of the CAS can be done in a number of ways and only an overview will be given here One method is via the configuration line CFG at the top of each menu The line shown right of CFG R X S means that the calculator is set to exact real mode that X is the current variable and you are working in Step by step mode If you select this ...

Page 363: ... you have made The only difference between the two configuration menus shown right is that the lower one is harder to use and contains one option not available on the upper one the ability to select French as the language in which the help screens are displayed The name of the current variable as well as the value of the variable MODULO can be changed by means of the SHIFT MODES view or by using t...

Page 364: ...ct Complex mode unless requested by the calculator in the performance of a particular operation Comment That says it all really You need to be concerned with this if you are finding roots of polynomials If Complex mode is not selected then only the real roots will be returned Verbose vs nonverbose mode When verbose mode is selected certain calculus applications are provided with comment lines in t...

Page 365: ...is selected non rational expressions will be automatically simplified Default selected Comment When this mode is not selected an expression such as the one shown right will not be simplified When selected it simplifies to I suggest that this is generally more desirable Calculator Tip of the CAS ly it in the introduction to this appendix on page 324 g i and pressing Changing the configuration can h...

Page 366: ...5 digits of the result Don t use a summation variable of lower case i This is assumed by the CAS to be the unit imaginary value the positive root of x2 1 0 Although you can use the integration symbol provided on the keyboard it has disadvantages outlined on page 74 Use the INTVX function instead See the example on page 339 The COLLECT function referred to earlier will factorize over the set of int...

Search results

Summary of Contents for 39gs

Reviews:

HP 39gs, Master Manual, Page: 120 / 366

Search results

Summary of Contents for 39gs

Reviews: