Lake Shore 321-01, Руководство пользователя

Страница: 121 / 130

Lake Shore Model 321 Autotuning Temperature Controller User’s Manual
Application Notes D-9
POLYNOMIAL REPRESENTATION
Curve 10 can be expressed by a polynomial equation based on the Chebychev polynomials. Four separate ranges are
required to accurately describe the curve. Table 1 lists the parameters for these ranges. The polynomials represent Curve
10 on the preceding page with RMS deviations of 10 mK. The Chebychev equation is:
T x a t x
i i
i
n
a f a f
=
=
∑
0
(1)
where T(x) = temperature in kelvin, t
i
(x) = a Chebychev polynomial, and a
i
= the Chebychev coefficient. The parameter x
is a normalized variable given by:
x
V VL VU V
VU VL
=
− − −
−
( ) ( )
( )
(2)
where V = voltage and VL and VU = lower and upper limit of the voltage over the fit range. The Chebychev polynomials
can be generated from the recursion relation:
t
i+1
(x) = 2xt
i
(x) - t
i-1
(x) (3)
t
0
(x) = 1, t
1
(x) = x
Alternately, these polynomials are given by: t
i
(x) = cos[i x arccos (x)] (4)
The use of Chebychev polynomials is no more complicated than the use of the regular power series and they offer
significant advantages in the actual fitting process. The first step is to transform the measured voltage into the normalized
variable using Equation 2. Equation 1 is then used in combination with equations 3 and 4 to calculate the temperature.
Programs 1 and 2 provide sample BASIC subroutines which will take the voltage and return the temperature T calculated
from Chebychev fits. The subroutines assume the values VL and V"U have been input along with the degree of the fit. The
Chebychev coefficients are also assumed to be in any array A(0), A(1),..., A(i
degree
).
An interesting property of the Chebychev fits is evident in the form of the Chebychev polynomial given in Equation 4. No
term in Equation 1 will be greater than the absolute value of the coefficient. This property makes it easy to determine the
contribution of each term to the temperature calculation and where to truncate the series if full accuracy is not required.
Program 1. BASIC Subroutine to evaluate temperature Program 2. BASIC Subroutine to evaluate temperature
T from the Chebychev series using Equations 1 and 3. T from the Chebychev series using Equations 1 and 4.
An array Tc (Ndegree) should be dimensioned. ACS is used to represent the arccosine function.
100 REM Evaluation of Chebychev series 100 REM Evaluation of Chebychev series
110 X = ((V-VL) -(VU-V)) / (VU-VL) 110 X = ((V-VL) -(VU-V)) / (VU-VL)
120 Tc(0) = 1 120 T = 0
130 Tc(1) = x 130 FOR I = 0 to Ndegree
140 T = A(0) + A(1) * X 140 T = T + A(I) * COS(I * ACS(X))
150 FOR I = 2 to Ndegree 150 NEXT I
160 Tc(I) = 2 * X * Tc(I-1) - Tc(I-2) 160 RETURN
170 T = T + A(I) * Tc(I)
180 NEXT I
190 RETURN
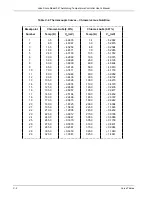
Table 1. Chebychev Fit Coefficients
2.0 K to 12.0 K 12.0 K to 24.5 K 24.5 K to 100.0 K 100 K to 475 K
VL = 1.32412 VL = 1.32412 VL = 1.32412 VL = 1.32412
VU = 1.69812 VU = 1.69812 VU = 1.69812 VU = 1.69812
A(0) = 7.556358 A(0) = 17.304227 A(0) = 71.818025 A(0) = 287.756797
A(1) = -5.917261 A(1) = -7.894688 A(1) = -53.799888 A(1) = -194.144823
A(2) = 0.237238 A(2) = 0.453442 A(2) = 1.669931 A(2) = -3.837903
A(3) = -0.334636 A(3) = 0.002243 A(3) = 2.314228 A(3) = -1.318325
A(4) = -0.058642 A(4) = 0.158036 A(4) = 1.566635 A(4) = -0.109120
A(5) = -0.019929 A(5) = -0.193093 A(5) = 0.723026 A(5) = -0.393265
A(6) = -0.020715 A(6) = 0.155717 A(6) = -0.149503 A(6) = 0.146911
A(7) = -0.014814 A(7) = -0.085185 A(7) = 0.046876 A(7) = -0.111192
A(8) = -0.008789 A(8) = 0.078550 A(8) = -0.388555 A(8) = 0.028877
A(9) = -0.008554 A(9) = -0.018312 A(9) = 0.056889 A(9) = -0.029286
A(10) = 0.039255 A(10) = -0.116823 A(10) = 0.015619
A(11) = 0.058580