Page 16-32
•
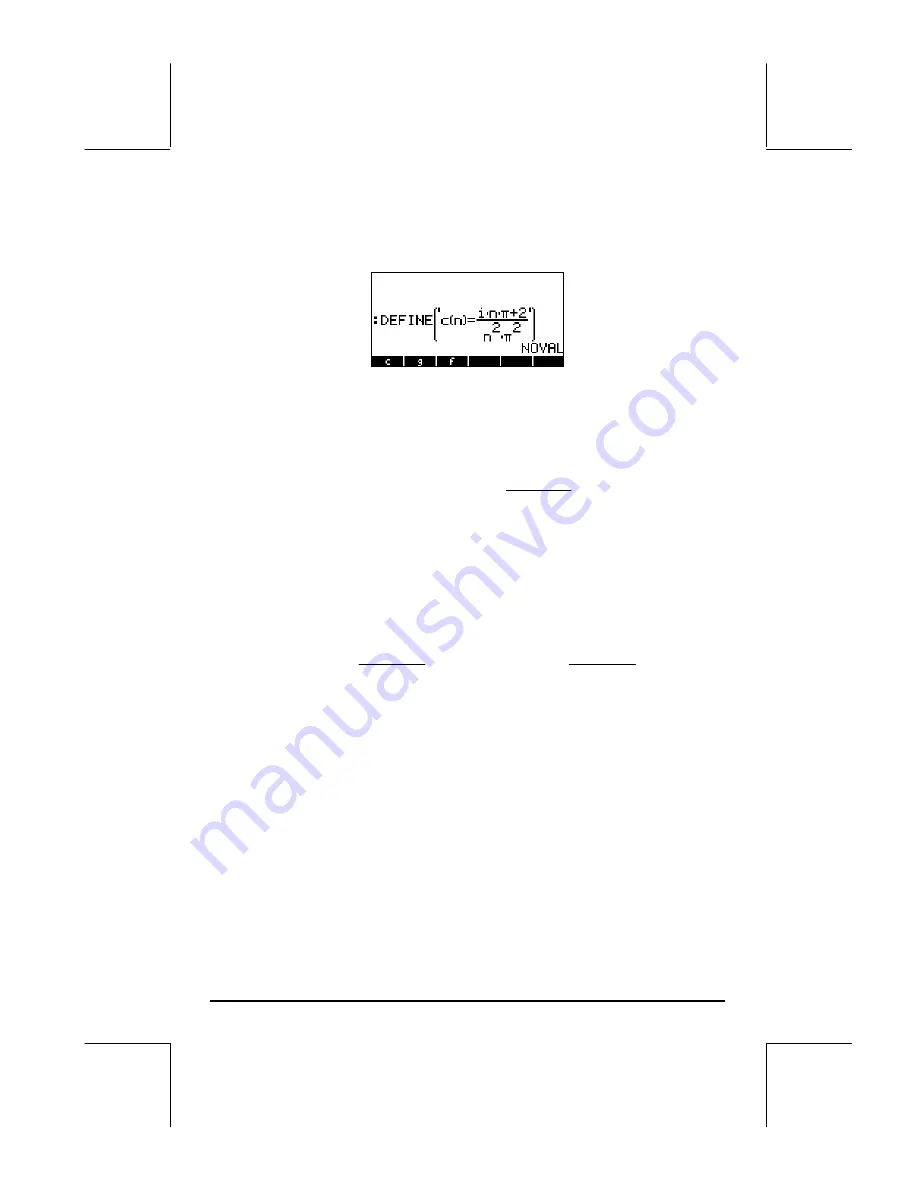
First, define a function c(n) representing the general term c
n
in the complex
Fourier series.
•
Next, define the finite complex Fourier series, F(X,k), where X is the
independent variable and k determines the number of terms to be used.
Ideally we would like to write this finite complex Fourier series as
)
2
exp(
)
(
)
,
(
X
T
n
i
n
c
k
X
F
k
k
n
⋅
⋅
⋅
⋅
⋅
=
∑
−
=
π
However, because the function c(n) is not defined for n = 0, we will be
better advised to re-write the expression as
+
=
0
)
0
,
,
(
c
c
k
X
F
)],
2
exp(
)
(
)
2
exp(
)
(
[
1
X
T
n
i
n
c
X
T
n
i
n
c
k
n
⋅
⋅
⋅
⋅
−
⋅
−
+
⋅
⋅
⋅
⋅
⋅
∑
=
π
π
Or, in the calculator entry line as:
DEFINE(‘F(X,k,c0) = c0+
Σ
(n=1,k,c(n)*EXP(2*i*
π
*n*X/T)+
c(-n)*EXP(-(2*i*
π
*n*X/T))’),
where T is the period, T = 2. The following screen shots show the definition of
function F and the storing of T = 2:






























