Page 11-9
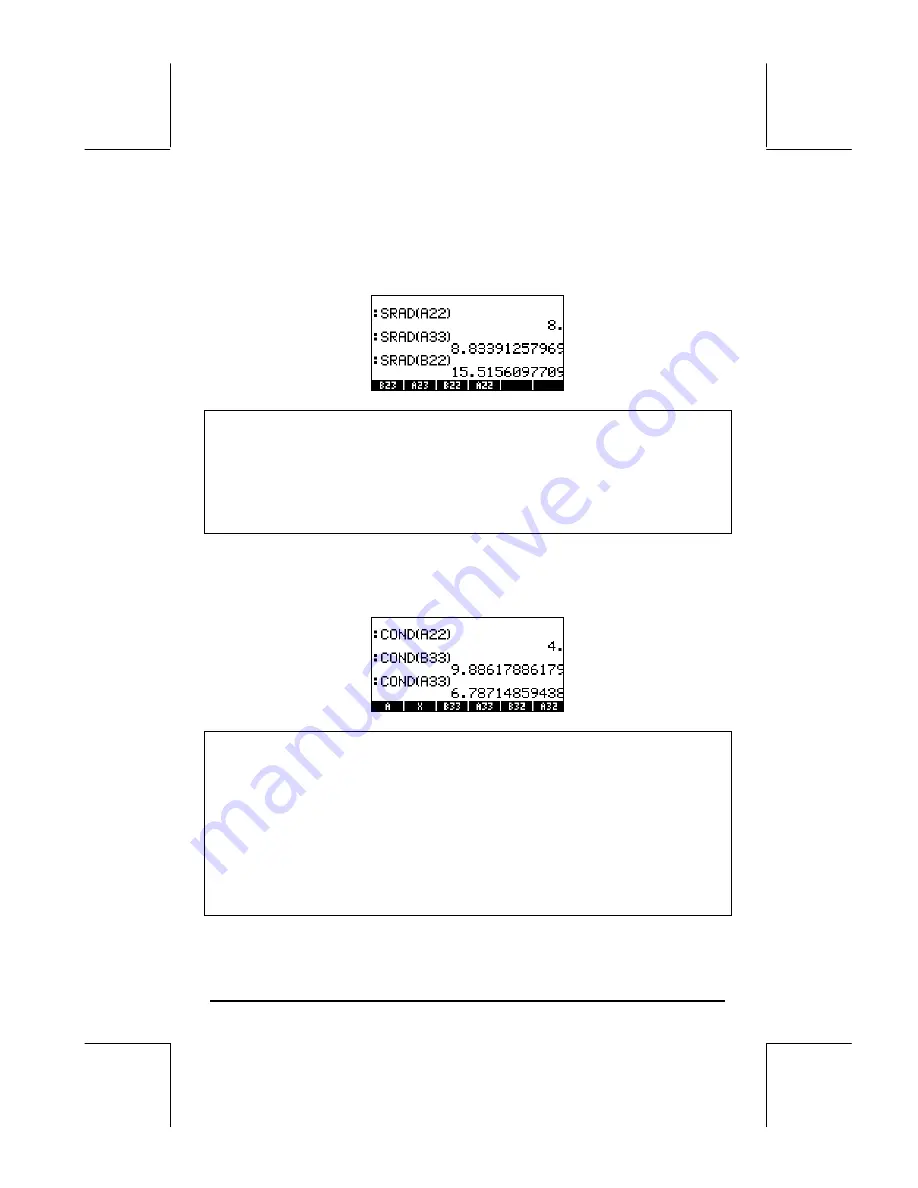
Function SRAD
Function SRAD determines the Spectral RADius of a matrix, defined as the
largest of the absolute values of its eigenvalues. For example,
Definition of eigenvalues and eigenvectors of a matrix
The eigenvalues of a square matrix result from the matrix equation
A
⋅
x
=
λ⋅
x
.
The values of
λ
that satisfy the equation are known as the eigenvalues of the
matrix
A
. The values of x that result from the equation for each value of l are
known as the eigenvectors of the matrix. Further details on calculating
eigenvalues and eigenvectors are presented later in the chapter.
Function COND
Function COND determines the condition number of a matrix. Examples,
Condition number of a matrix
The condition number of a square non-singular matrix is defined as the
product of the matrix norm times the norm of its inverse, i.e.,
cond(
A
) = ||
A
||×||
A
-1
||. We will choose as the matrix norm, ||
A
||, the
maximum of its row norm (RNRM) and column norm (CNRM), while the norm
of the inverse, ||
A
-1
||, will be selected as the minimum of its row norm and
column norm. Thus, ||
A
|| = max(RNRM(
A
),CNRM(
A
)), and ||
A
-1
|| =
min(RNRM(
A
-1
), CNRM(
A
-1
)).






























