Page 7-6
Example 2 - Entrance from a lake into an open channel
This particular problem in open channel flow requires the simultaneous
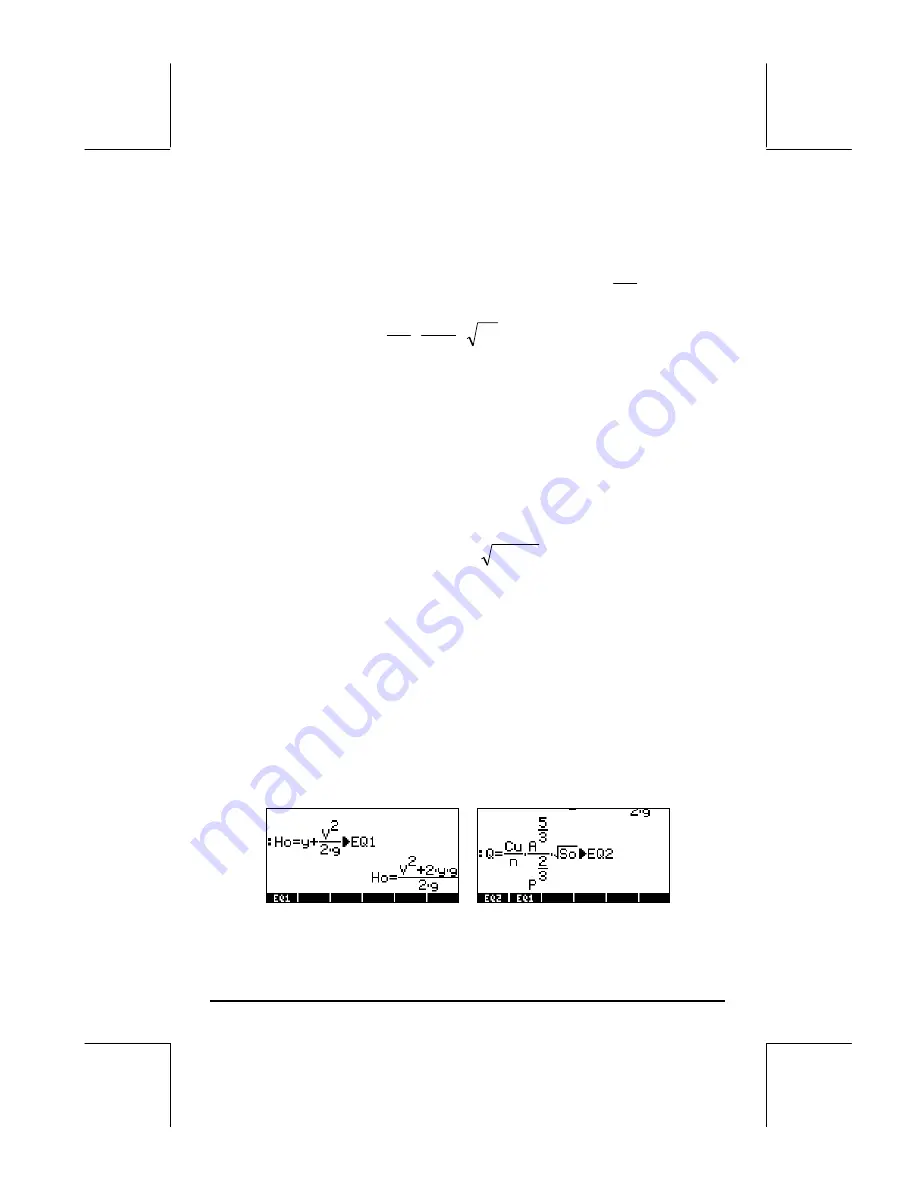
solution of two equations, the equation of energy:
g
V
y
H
o
2
2
+
=
, and
Manning’s equation:
o
S
P
A
n
Cu
Q
⋅
⋅
=
3
/
2
3
/
5
. In these equations, H
o
represents the energy head (m, or ft) available for a flow at the entrance to a
channel, y is the flow depth (m or ft), V = Q/A is the flow velocity (m/s or
ft/s), Q is the volumetric discharge (m
3
/s or ft
3
/s), A is the cross-sectional
area (m
2
or ft
2
), C
u
is a coefficient that depends on the system of units (C
u
=
1.0 for the SI, C
u
= 1.486 for the English system of units), n is the Manning’s
coefficient, a measure of the channel surface roughness (e.g., for concrete, n
= 0.012), P is the wetted perimeter of the cross section (m or ft), S
o
is the
slope of the channel bed expressed as a decimal fraction. For a trapezoidal
channel, as shown below, the area is given by
y
my
b
A
)
(
+
=
, while the
wetted perimeter is given by
2
1
2
m
y
b
P
+
+
=
, where b is the bottom
width (m or ft), and m is the side slope (1V:mH) of the cross section.
Typically, one has to solve the equations of energy and Manning’s
simultaneously for y and Q. Once these equations are written in terms of the
primitive variables b, m, y, g, S
o
, n, Cu, Q, and H
o
, we are left with a system
of equations of the form f
1
(y,Q) = 0, f
2
(y,Q) = 0. We can build these two
equations as follows.
We assume that we will be using the ALG and Exact modes in the calculator,
although defining the equations and solving them with MSLV is very similar in
the RPN mode. Create a sub-directory, say CHANL (for open CHANneL),
and within that sub-directory define the following variables:






























