Page 16-26
Again, there is a new component to the motion switched at t=3, namely, the
particular solution y
p
(t) = [1+sin(t-3)]
⋅
H(t-3), which changes the nature of the
solution for t>3.
The Heaviside step function can be combined with a constant function and
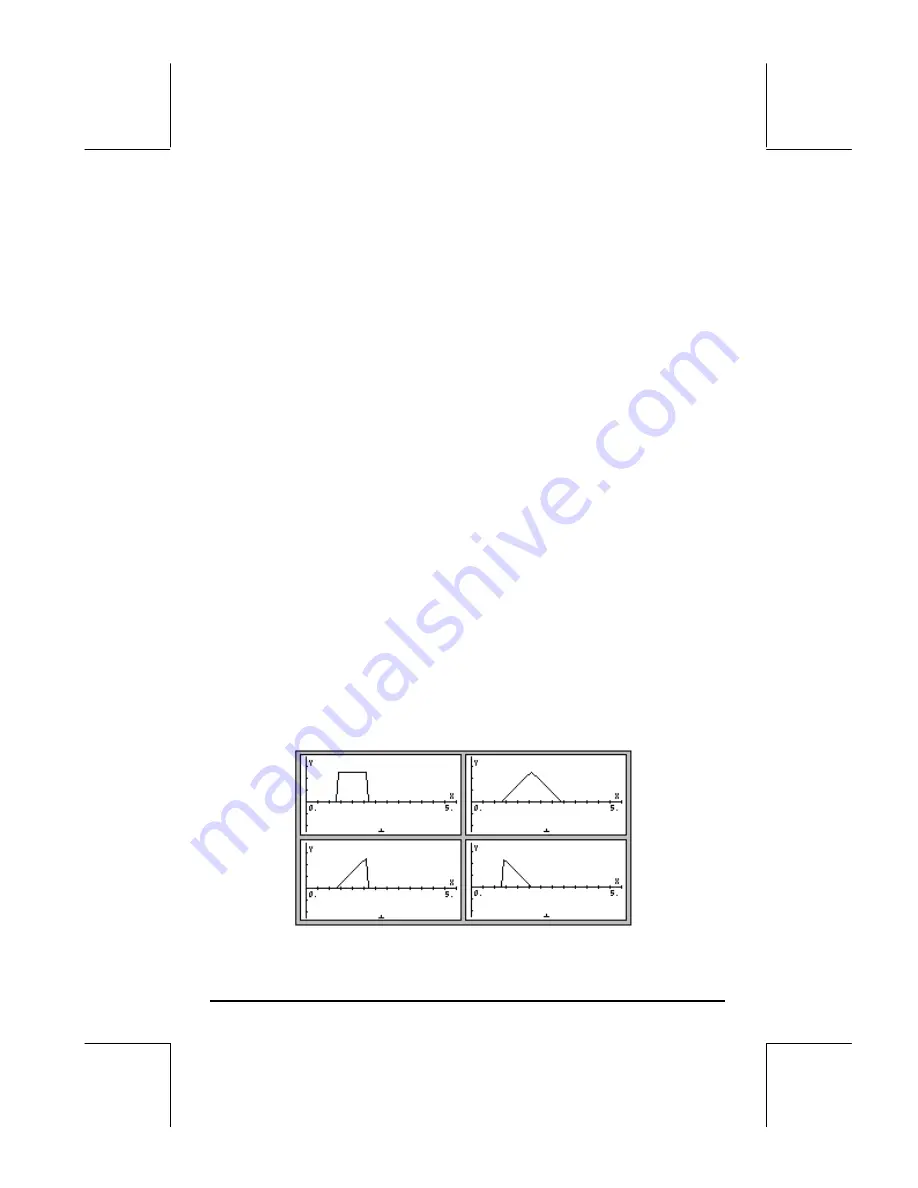
with linear functions to generate square, triangular, and saw tooth finite pulses,
as follows:
•
Square pulse of size U
o
in the interval a < t < b:
f(t) = Uo[H(t-a)-H(t-b)].
•
Triangular pulse with a maximum value Uo, increasing from a < t < b,
decreasing from b < t < c:
f(t) = U
o
⋅
((t-a)/(b-a)
⋅
[H(t-a)-H(t-b)]+(1-(t-b)/(b-c))[H(t-b)-H(t-c)]).
•
Saw tooth pulse increasing to a maximum value Uo for a < t < b,
dropping suddenly down to zero at t = b:
f(t) = U
o
⋅
(t-a)/(b-a)
⋅
[H(t-a)-H(t-b)].
•
Saw tooth pulse increasing suddenly to a maximum of Uo at t = a, then
decreasing linearly to zero for a < t < b:
f(t) = U
o
⋅
[1-(t-a)/(b-1)]
⋅
[H(t-a)-H(t-b)].
Examples of the plots generated by these functions, for Uo = 1, a = 2, b = 3,
c = 4, horizontal range = (0,5), and vertical range = (-1, 1.5), are shown in
the figures below:






























