Concepts and features
R&S
®
ZNB/ZNBT
121
User Manual 1173.9163.02 ─ 62
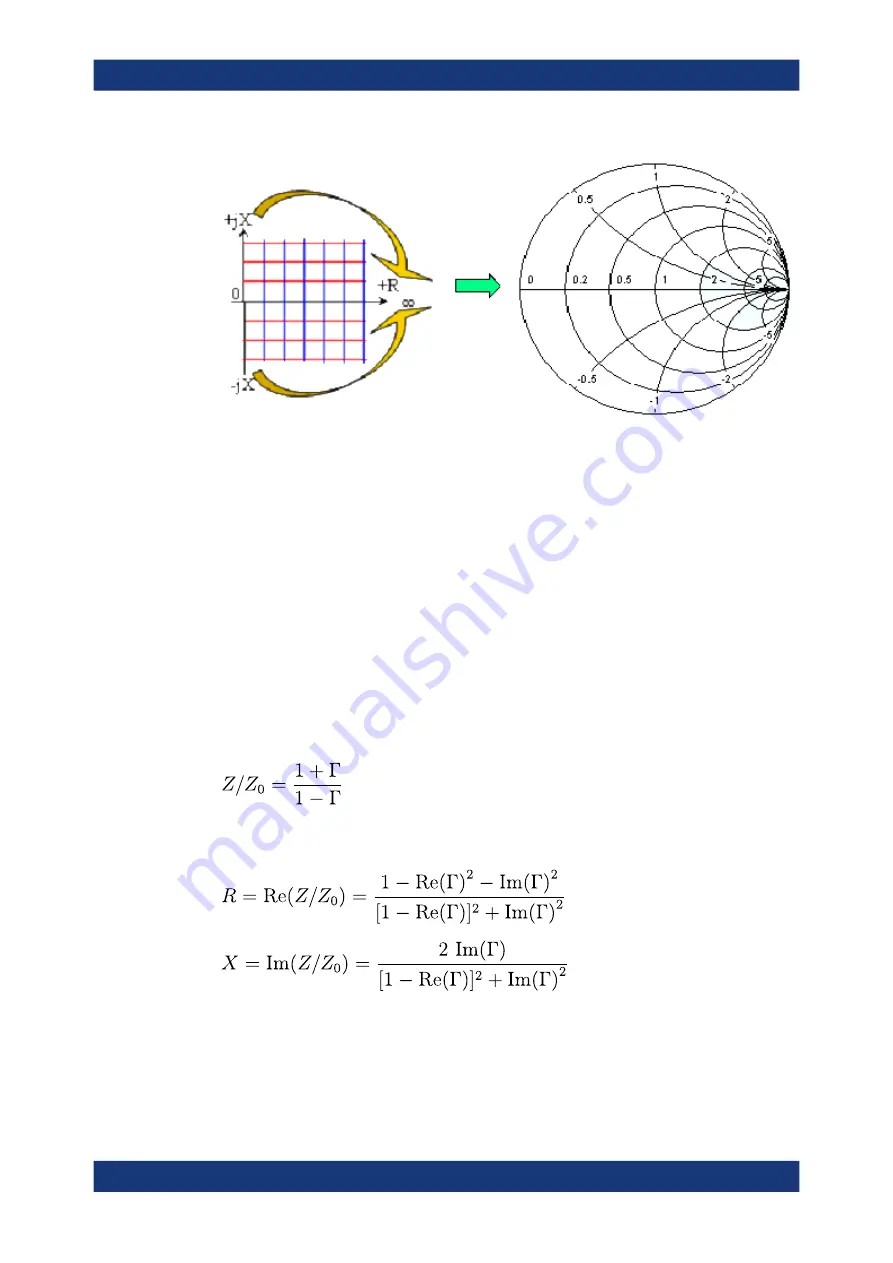
The basic properties of the Smith chart follow from this construction:
●
The central horizontal axis corresponds to zero reactance (real impedance). The
center of the diagram represents Z/Z
0
= 1 which is the reference impedance of the
system (zero reflection). At the left and right intersection points between the hori-
zontal axis and the outer circle, the impedance is zero (short) and infinity (open).
●
The outer circle corresponds to zero resistance (purely imaginary impedance).
Points outside the outer circle indicate an active component.
●
The upper and lower half of the diagram correspond to positive (inductive) and
negative (capacitive) reactive components of the impedance, respectively.
Example: Reflection coefficients in the Smith chart
If the measured quantity is a complex reflection coefficient
Γ
(e.g. S
11
, S
22
), then the
unit Smith chart can be used to read the normalized impedance of the DUT. The coor-
dinates in the normalized impedance plane and in the reflection coefficient plane are
related as follows (see also: definition of matched-circuit (converted) impedances):
From this equation, it is easy to relate the real and imaginary components of the com-
plex resistance to the real and imaginary parts of
Γ
:
According to the two equations above, the graphical representation in a Smith chart
has the following properties:
●
Real reflection coefficients are mapped to real impedances (resistances).
●
The center of the
Γ
plane (
Γ
= 0) is mapped to the reference impedance Z
0
,
whereas the circle with |
Γ
| = 1 is mapped to the imaginary axis of the Z plane.
Screen elements
















































