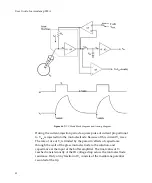
User
Guide
for
Axoclamp
900A
range
from
20
to
50,000.
If
K
were
unity,
the
error
would
vary
from
3
percent
down
to
0.01
percent.
However,
K
is
always
less
than
unity,
so
the
error
is
worse.
If
the
output
micropipette
resistance
is
90
M
Ω
and
the
membrane
resistance
is
10
M
Ω
,
K
is
0.1
and
the
error
is
ten
times
worse
than
if
K
were
unity.
Further,
during
activation
of
membrane
currents
R
m
can
drop
dramatically,
and
K
becomes
equal
to
R
m
/
R
e2
.
Thus,
as
a
rule
of
thumb
it
is
desirable
to
use
an
output
micropipette
whose
resistance
is
as
low
as
possible,
ideally
smaller
than
the
resting
membrane
resistance.
Step
Response
and
Bandwidth
After
a
step
command,
the
membrane
potential
relaxes
exponentially
towards
its
new
value.
For
μ
K
>>
1,
the
time
constant
for
the
relaxation
is:
μ
C
R
τ
m
e
2
=
Increasing
the
clamp
gain
decreases
the
time
constant
for
the
step
response.
For
example,
if
R
e2
=
10
M
Ω
,
C
m
=
1000
pF
and
μ
=
100,
the
time
constant
is
100
μ
s.
Stated
differently,
increasing
the
clamp
gain
also
increases
the
bandwidth
with
which
V
m
can
follow
changes
in
V
cmd
.
The
–3
dB
frequency
of
the
bandwidth
is:
m
e
dB
C
R
π
μ
f
2
3
2
=
Stability
An
ideal
voltage
clamp
is
unconditionally
stable.
The
membrane
capacitance
provides
a
90°
phase
shift,
which
is
required
for
stability
in
all
negative
feedback
circuits.
Unfortunately,
in
the
real
world
other
factors
combine
to
make
the
circuit
unstable
at
high
clamp
gains.
The
coupling
capacitance
(C
x
)
between
the
microelectrodes
is
extremely
destabilizing.
Values
as
small
as
0.01
pF
can
lead
to
oscillation
if
μ
has
a
magnitude
of
several
hundred
or
more.
104