Equations
E1
and
E2
These two equations can be used for calculations involving individual and cumulative Binomial probabilities.
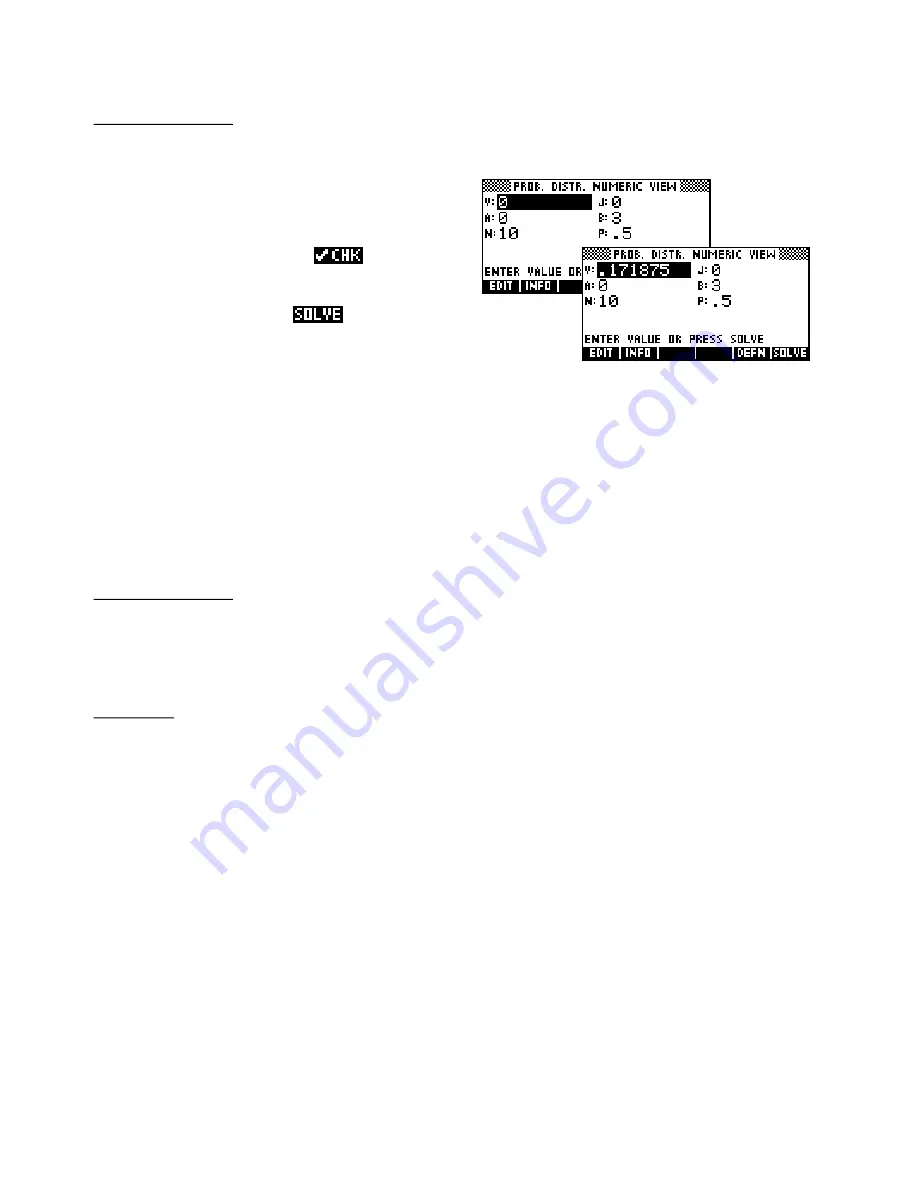
eg. Find the probability of at most 3 heads when
tossing a coin 10 times.
Ensure that formula
E2
is
ed and enter
the values shown right. The value in
J
is
irrelevant as it is merely the summation variable.
Highlight
V
and press
.
Answer: 0.1719
Note:
If N is larger than 200 then you should use a Normal approximation. The
N!/((N-R)!*R!)
section of
the formula will cause internal overflow and inaccurate answers above this level. The time needed to
perform the summation will probably also be excessive. Solve works by repeated iterations
converging on the correct value and this will be quite slow if the summation has many terms. If it is
important not to use a Normal approximation then replace the
N!/((N-R)!*R!)
portion with
COMB(N,R)
. The
COMB
function has special facilities for handling large numbers. This will not help
greatly with the iteration time needed.
Equations
E3
and
E4
These two equations can be used for calculations involving individual and cumulative Poisson probabilities,
where
M
is the mean. The technique is otherwise identical to the Binomial problem.
Equation
E5
The formula in
E5
is a generic formula for problems such as the one below:
(
“A probability distribution has the equation
f x
)
=
0.625
x
3
(
2
−
x
)
; 0
≤
x
≤
2
. Show
(
that this is a valid probability distribution function and use it to find
P x
≤
1.2
)
”
Use it by substituting whatever function is in use for the one currently entered. As this formula involves the
integration function, each use of the solve process will require the calculator to perform multiple integrations.
Because of this the solving process will be relatively slow.
233