Finding an inverse matrix
⎡
2
1
4
⎤
1
Eg. 2 Find the inverse matrix
A
−
for the matrix
A
= ⎢⎢
1
1
3
⎥
⎥
⎢−
2
4
−
1
⎥⎦
⎣
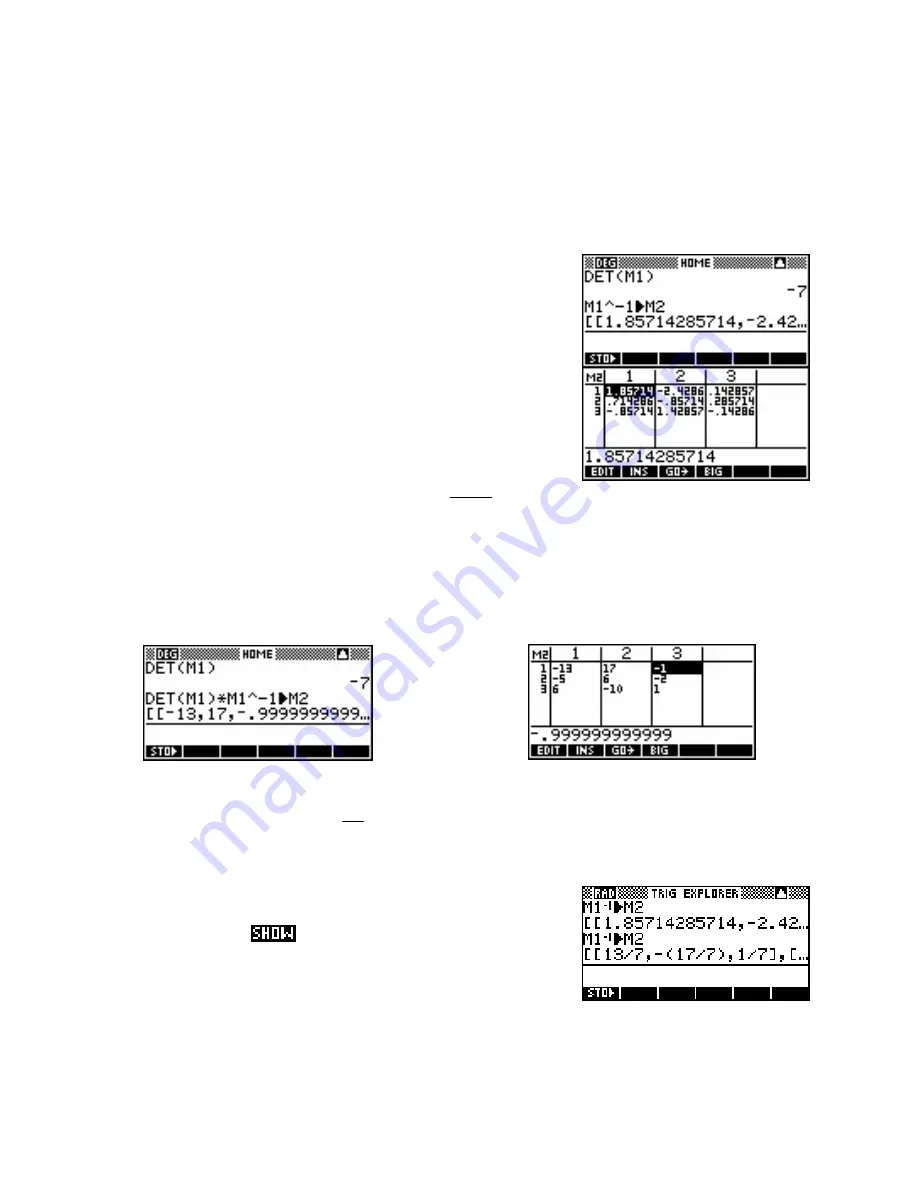
The first step is to store the matrix A into
M1
. If you now simply store its
inverse into
M2
you will find, depending on the determinant, that the
result is probably a collection of decimal values (see right).
This answer is correct and we could stop there. However, this is not the
best way to display the answer. The fact that the determinant is
incorporated into the inverse makes whole numbers unlikely.
1
A better way is often to write the answer as a fraction
multiplied
det
( )
A
by a matrix of whole numbers. If we multiply the inverse by the determinant then we can usually remove the
fractions.
i.e.
with
M2
being…
⎡−
13 17
−
1
⎤
Thus we can finally write:
A
=
−
1
7
⎢
⎢ −
5
6
−
2
⎥
⎥
⎢
6
−
10
1
⎥⎦
⎣
An alternative to this is to change into
Fraction 6
numeric format in the
MODES
view. This will give a matrix of fractional values which can be
seen more clearly using
.
213