51
Note:
The reference can also be input via panel or serial port.
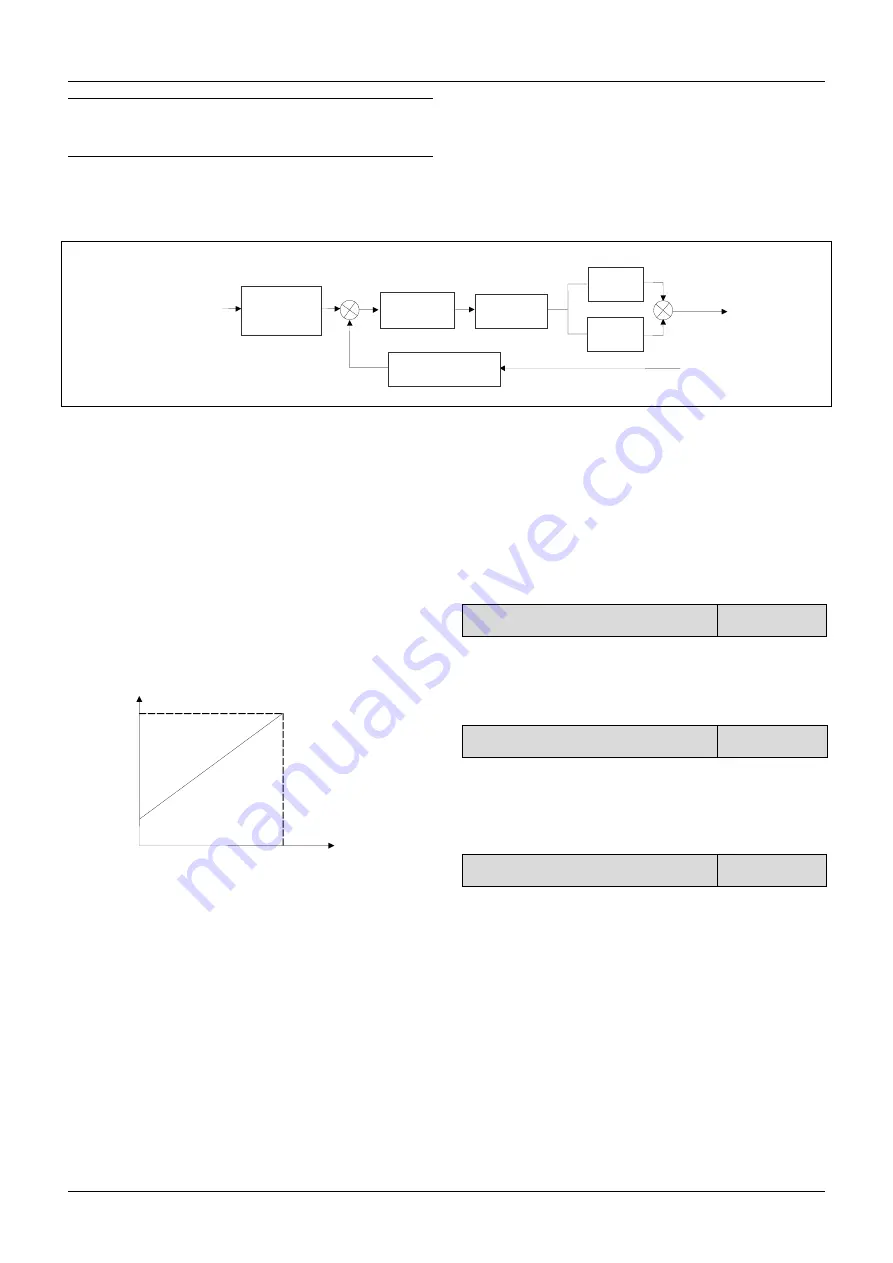
Operating principles of internal process close-loop of
CV100 is shown in the Fig. 6-38.
In the above Fig., KP: proportional gain; Ki: integral
gain
In Fig. 6-40, refer to C1.00~C1.14 for the definitions of
close-loop reference, feedback, error limit and
proportional and Integral parameters.
Fig.6-40 Principle diagram of process close-loop control
There are two features of internal close-loop of CV100:
The relationship between reference and feedback can be
defined by C1.05
~
C1.08
For example: In Fig. 6-38, if the reference is analog
signal of -10~10V, the controlled value is 0~1MP, and
the signal of pressure sensor is 4~20mA, then the
relationship between reference and feedback is shown
in Fig. 6-41.
Fig.6-41 Reference and feedback
After the control type is determined, follow the
procedures below to set close loop parameters.
1)Determine the close-loop reference and feedback
channel (C1.01 and C1.02);
2)The relationship between close-loop reference and
feedback value (C1.05
~
C1.08) should be defined for
analog close-loop control;
3)Determine the close-loop regulation characteristic, if
the relationship between motor speed and the reference
is opposite,then set the close-loop regulation
characteristic as negative characteristic(C1.15=1).
4)Set up the integral regulation function and close-loop
frequency presetting function (C1.16
~
C1.18);
5)Adjust the close-loop filtering time, sampling cycle,
error limit and gain(C1.09
~
C1.14).
C1.00 Close-loop control function
0
、
1
【
0
】
0
:
Disable.
1
:
Enable.
C1.01 Reference channel selection
0
、
1
、
2
、
3
【
1
】
0: digital input(Take the value of C1.03).
1: AI1 analog input.
2: AI2 analog input
C1.02 Feedback channel selection
0
~
5
【
1
】
0
:
AI1 analog input
1
:
AI2 analog input
2
:
AI1+ AI2
3
:
AI1
-
AI2
4
:
Min{ AI1
,
AI2}
5
:
Max{ AI1
,
AI2}
6
:
DI (Pulse)
Settings of AI are the same as above.
1
0
V
-
1
0
V
Referenc
4
m
A
2
0
m
A
Feedbac
Reference
Reference
regulation
(
C
1
.
0
5
、
C
1
.
0
7
)
ε
Error limit
(
C
1
.
1
4
)
+
-
Feedback
K
P
×
(
C
1
.
0
9
)
K
i
×
(
C
1
.
1
0
)
Regulation
(
C
1
.
1
5
)
ε
ε
∑
+
+
Output
Feedback regulation
(
C
1
.
0
6
、
C
1
.
0
8
)