Continuous Stiffness Measurement A
Agilent Nano Indenter G200 User’s Guide
A-9
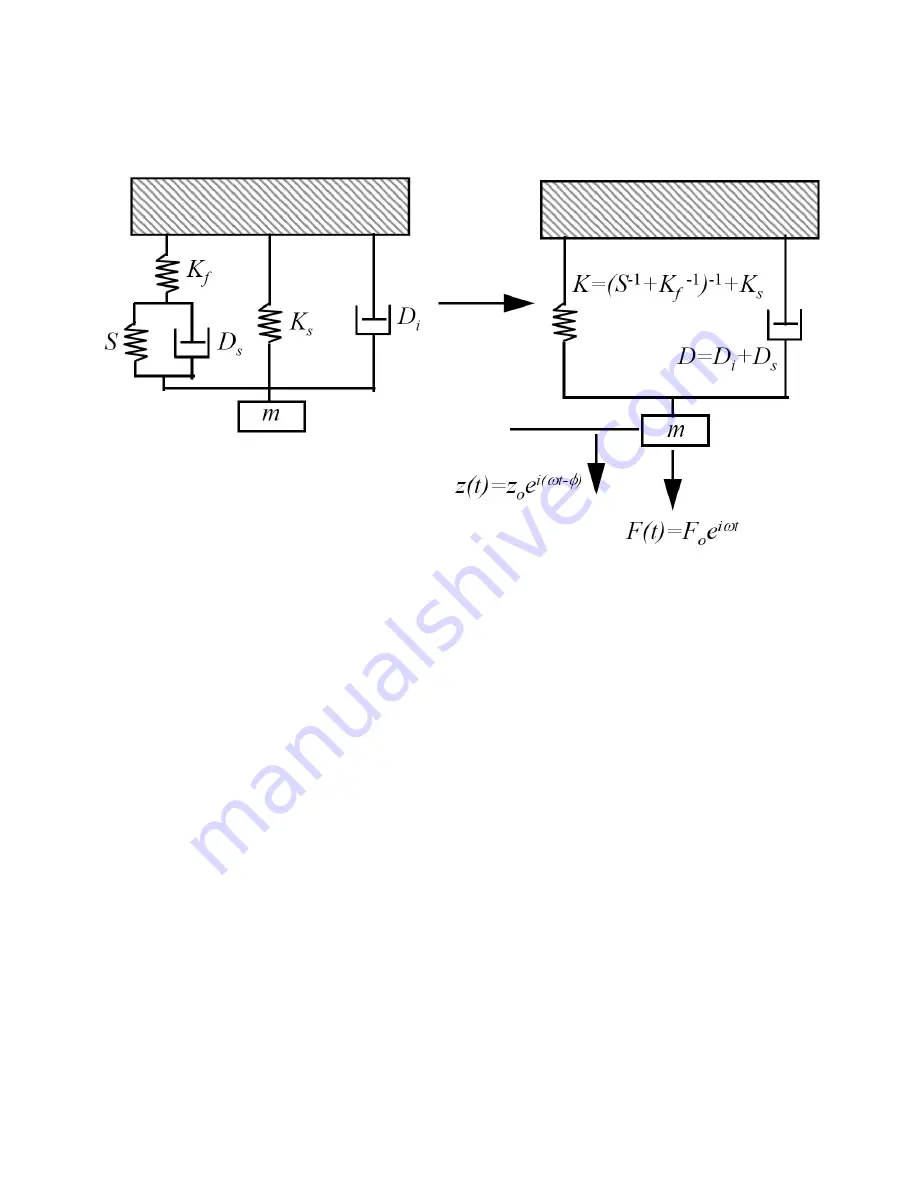
Figure A-6
Harmonic oscillator models
The analysis of a simple harmonic oscillator subject to a forced
oscillation may be found in any first course on differential equations or
vibrations. A force summation on the mass yields the ordinary
differential equation:
(34)
where
K
is an equivalent stiffness, which includes the stiffness of the
contact,
S
, the load-frame stiffness,
K
f
, and the stiffness of the support
springs,
K
s
; that is:
(35)
mz
··
Dz
·
Kz
+
+
F t
=
K
S
1
–
K
f
1
–
+
K
s
+
=