Electro
Industries/GaugeTech
The Leader In Power Monitoring and Smart Grid Solutions
Doc
#
E149701
1-7
1: Three-Phase Power Measurement
Some digital meters measure the individual phase power values one phase at a time.
This means the meter samples the voltage and current on one phase and calculates a
power value. Then it samples the second phase and calculates the power for the sec-
ond phase. Finally, it samples the third phase and calculates that phase power. After
sampling all three phases, the meter adds the three readings to create the equivalent
three-phase power value. Using mathematical averaging techniques, this method can
derive a quite accurate measurement of three-phase power.
More advanced meters actually sample all three phases of voltage and current
simultaneously and calculate the individual phase and three-phase power values. The
advantage of simultaneous sampling is the reduction of error introduced due to the
difference in time when the samples were taken.
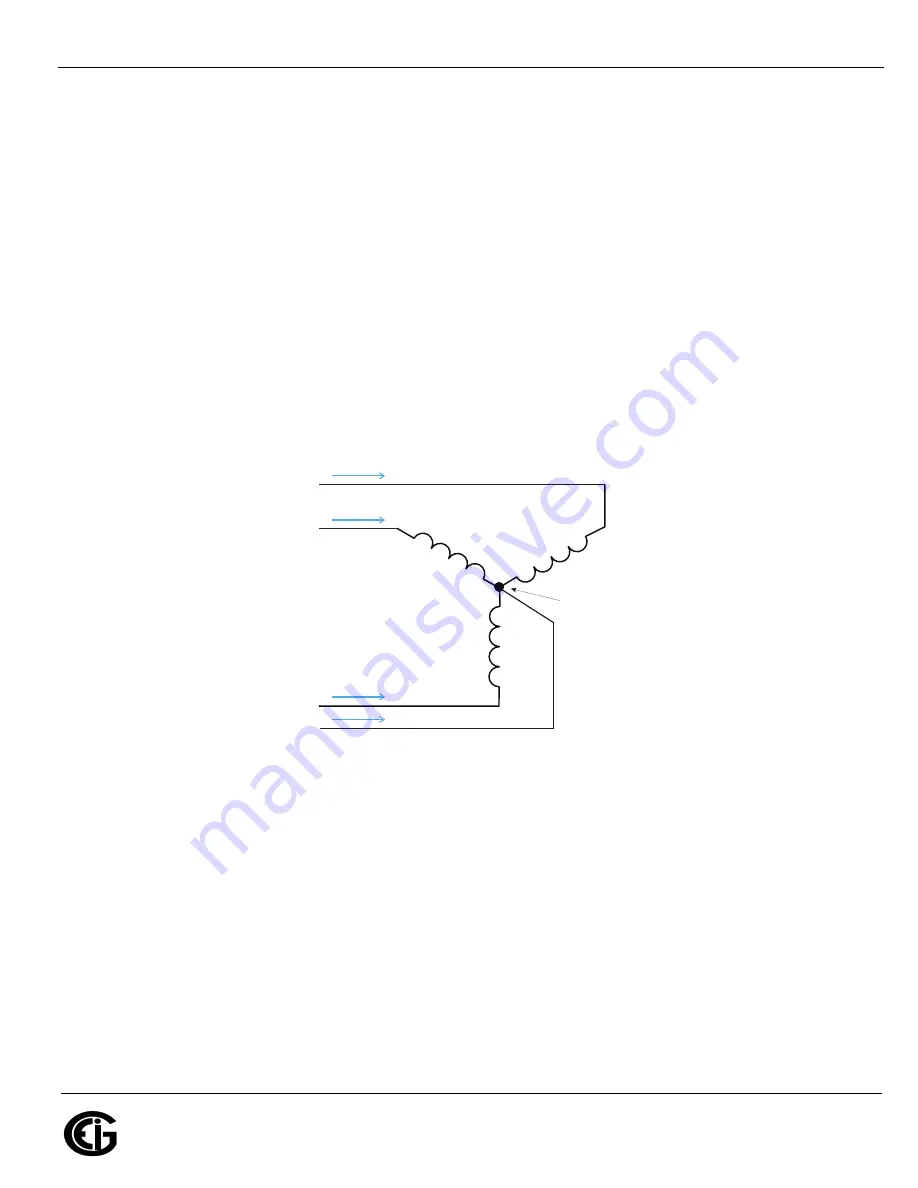
Figure 1.6: Three-Phase Wye Load Illustrating Kirchhoff’s Law and Blondel’s Theorem
Blondel's Theorem is a derivation that results from Kirchhoff's Law. Kirchhoff's Law
states that the sum of the currents into a node is zero. Another way of stating the
same thing is that the current into a node (connection point) must equal the current
out of the node. The law can be applied to measuring three-phase loads. Figure 1.6
shows a typical connection of a three-phase load applied to a three-phase, four-wire
service. Kirchhoff's Law holds that the sum of currents A, B, C and N must equal zero
or that the sum of currents into Node "n" must equal zero.
If we measure the currents in wires A, B and C, we then know the current in wire N by
Kirchhoff's Law and it is not necessary to measure it. This fact leads us to the
conclusion of Blondel's Theorem- that we only need to measure the power in three of
Phase B
Phase C
Phase A
A
B
C
N
Node "n"
Summary of Contents for Shark 200
Page 1: ...V 1 24 March 15 2018 ...
















































