Section 3
Theory of Operation
3-3
V = k(
ν
r
-
ν
s
)
3-1
The analyzer operates in such a way as to keep
ν
r
constant, so we can factor
ν
r
out of the quantity in parentheses, define K = k
ν
r
, and obtain,
V
K
s
r
=
−
1
υ
υ
3-2a
In absolute mode, the instrument is operated with no CO
2
in the reference
cell so
ν
r
is proportional to maximum photon throughput. The sample cell
normally contains CO
2
, which reduces the photon flux reaching the detector
through the sample cell and reduces
ν
s
. Therefore, the ratio
ν
s
/
ν
r
gives the
ratio of photon flux in the presence of CO
2
and in its absence, which is just
the transmittance
τ
. Since absorptance A equals 1-
τ
, we can also write
equation 3-2 as
V = K(1 -
τ
)
3-2b
and
V = KA
3-2c
The constant K is given on the calibration sheet.
Equation 3-2c indicates that the analyzer output voltage is proportional to
absorptance; however, absorptance is a non-linear function of CO
2
mole
fraction. Absorptance and analyzer output voltage both increase with
increasing CO
2
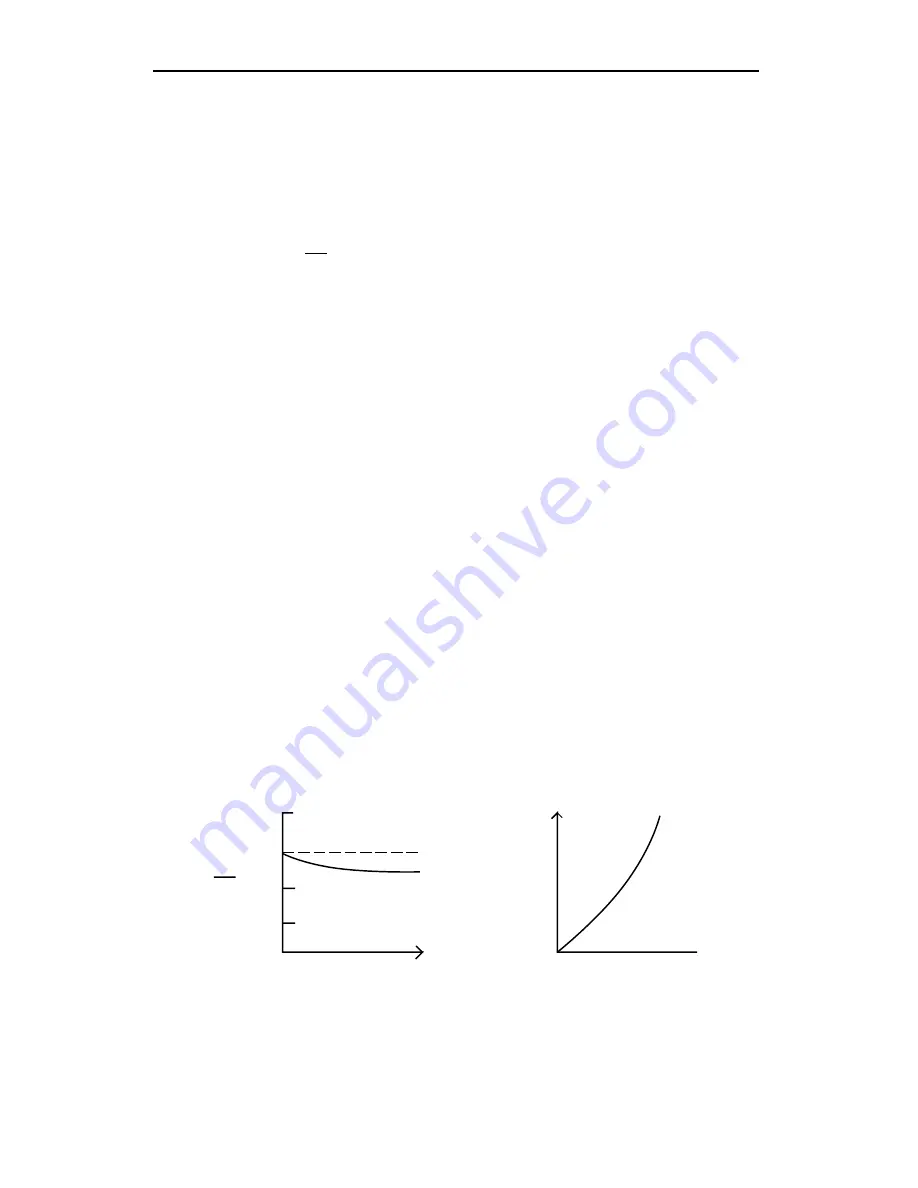
mole fraction in the sample cell. Figure 3-1 illustrates a
typical relationship between gas concentration, transmittance (
ν
s
/
ν
r
) and
analyzer output voltage.
1.2
1.0
0.8
0.6
0
(A)
Gas Conc.
ν
s
ν
r
(B)
Gas Conc.
V (volts)
V= K(1-
τ
)
F(V)
0
Figure 3-1.
(A) The ratio of detector output while viewing the sample cell (
ν
s) and
the reference cell (
ν
r) decreases with increasing gas concentration. (B) The output
voltage V is related to the ratio of
ν
s to
ν
r by Equation (3-2a). Gas concentration in
terms of V is the calibration function F(V).






























