Hioki MEMORY HiCORDER 8855, Инструкция по эксплуатации

Страница: 240 / 264

APPENDIX 18
────────────────────────────────────────────────────
Appendix 3 Reference
────────────────────────────────────────────────────
h(t)
H(
ω
)
fin(t)
Fin(
ω
)
fout(t)
Fout(
ω
)
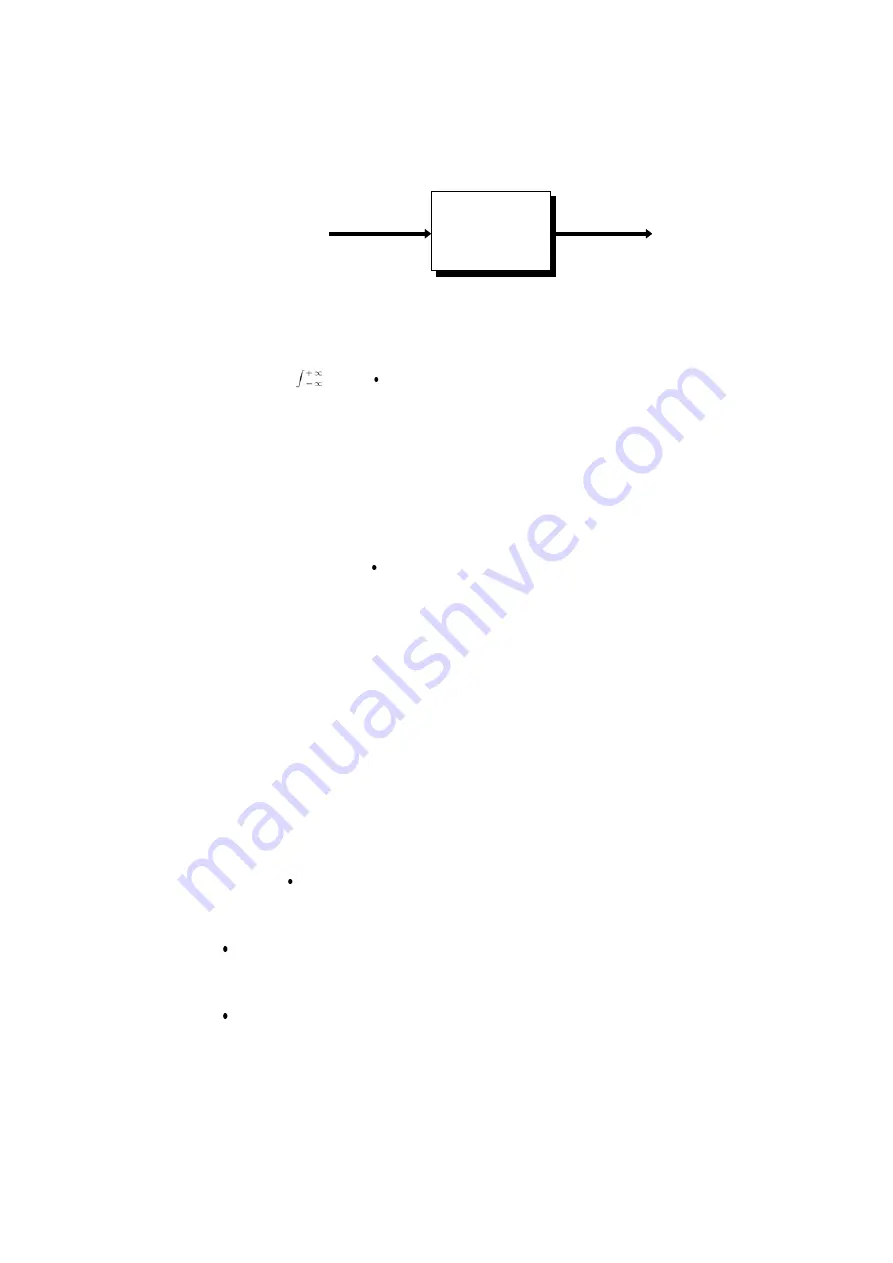
Output
Input
ˆ Application of Fourier transform (transfer function, unit-impulse
response)
As an application of Fourier transform, this section describes a steady-state
response in a static linear system.
fin(t): time function of input (source signal)
fout(t): time function of output (response function)
h(t): unit impulse response of linear system
t ,
τ : time
fout(t) = fin(
τ
) h(t-
τ
)d
τ
5
The relationship between the input and output is expressed as follows:
This indicates that the response of the linear system can be determined just
by knowing the unit impulse response h(t) of the system.
In the frequency domain, Fin(
ω ), Fout( ω ), H( ω ), and ω are defined as follows
Fin( ω ): Fourier transformation of fin(t)
Fout( ω ): Fourier transformation of fout(t)
H( ω ): Fourier transformation of h(t)
ω : Angular frequency
Fout ( ω ) = Fin( ω )
H
( ω )
6
Therefore, when fin(t) and fout(t) are measured, the system transfer function
H (
ω ) and the unit impulse response h(t) can be obtained by performing an
FFT operation and an inverse FFT operation.
ˆ Aliasing
When the frequency of the signal to be measured approaches the sampling
frequency, beyond a certain point the measured signal frequency will be
lower than the actual signal frequency. In such a case, frequency components
that do not exist will appear in the waveform along the frequency axis. This
phenomenon is called aliasing, and it occurs if sampling is carried out at a
frequency lower than the so-called Nyquist frequency determined by
Nyquist's sampling theorem.
Sampling theorem
Fs = 2 Fmax
1
Fmax : Highest frequency component to be measured
Fs : Sampling frequency (Nyquist frequency)
In order to be able to restore the original waveform from the sampling data,
the sampling frequency must be at least twice as high as the signal
frequency.
If sampling is carried out at a frequency lower than the Nyquist frequency,
frequency components above 1/2 of the sampling frequency will be aliased to
lower frequencies, and the measured signal will appear to contain frequency
components that actually do not exist.