Danfoss VLT 6000 HVAC Profibus, Руководство пользователя

Страница: 163 / 177

VLT
®
6000 HVAC
163
MG.60.B1.02 - VLT is a registered Danfoss trade mark
All about
VL
T 6000 HV
AC
The voltage distortion on the mains supply depends
on the size of the harmonic currents multiplied by the
mains impedance for the frequency in question.
The total voltage distortion THD is calculated on the
basis of the individual voltage harmonics using the
following formula:
THD% = U 2 + U 2 + ..... U 2
Some of the harmonic currents might disturb
communication equipment connected to the same
transformer or cause resonance in connection with
power-factor correction batteries. VLT 6000 HVAC
has been designed in accordance with the following
standards:
- IEC 1000-3-4
- IEEE 519-1992
- IEC 22G/WG4
- EN 50178
- VDE 160, 5.3.1.1.2
5
+ U
7
+ ..... U
N
■ ■
■ ■
■
Mains supply interference/harmonics
A frequency converter takes up a non-sinusoidal
current from mains, which increases the input current
I
RMS
. A non-sinusoidal current can be transformed by
means of a Fourier analysis and split up into sine
wave currents with different frequencies, i.e. different
harmonic currents I
N
with 50 Hz as the basic
frequency:
Harmonic currents I
1
I
5
I
7
Hz 50 Hz 250 Hz 350 Hz
The harmonics do not affect the power consumption
directly, but increase the heat losses in the installation
(transformer, cables). Consequently, in plants with a
rather high percentage of rectifier load, it is important
to maintain harmonic currents at a low level to avoid
overload of the transformer and high temperature in
the cables.
Harmonic currents compared to the RMS input
current:
Input current
I
RMS
1.0
I
1
0.9
I
5
0.4
I
7
0.3
I
11-49
< 0.1
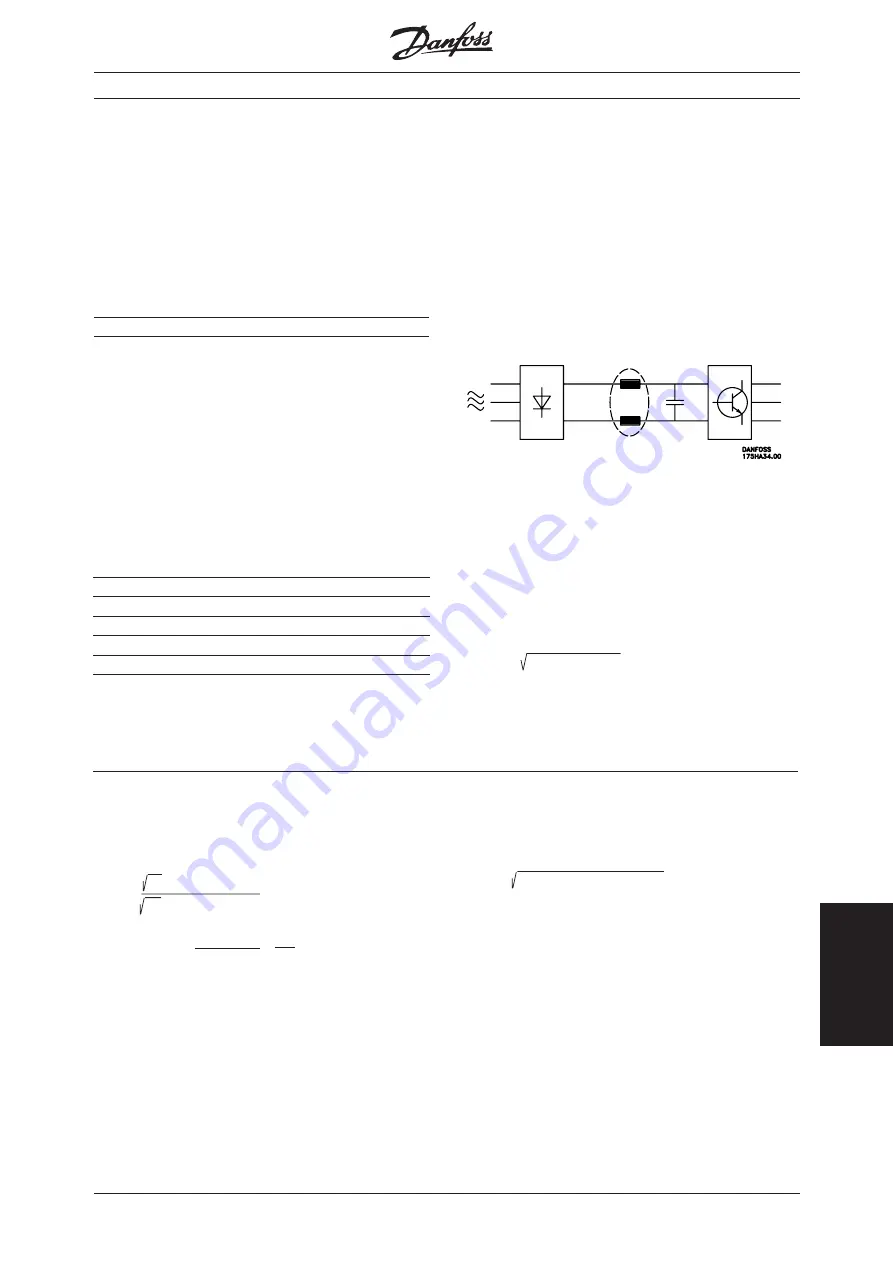
To ensure low, harmonic currents, VLT 6000 HVAC
has intermediate circuit coils as standard. This
normally reduces the input current I
RMS
by 40%.
Power factor = =
Power factor
The power factor is the relation between I
1
and I
RMS
.
The power factor for 3-phase control
=
The power factor indicates the extent to which the
frequency converter imposes a load on the mains
supply.
The lower the power factor, the higher the I
RMS
for the
same kW performance.
3 x U x I
1
x cos
ϕ
1
3 x U x I
RMS
I
R M S
I
1
I
R M S
■
I
RMS
= I
1
2 + I
5
2 + I
7
2 + . . . + I
n
2
I
1
x cos
ϕ
1
since cos
ϕ
= 1
In addition, a high power factor indicates that the
different harmonic currents are low.
(U
N
% of U)