Page 16-19
The result is:
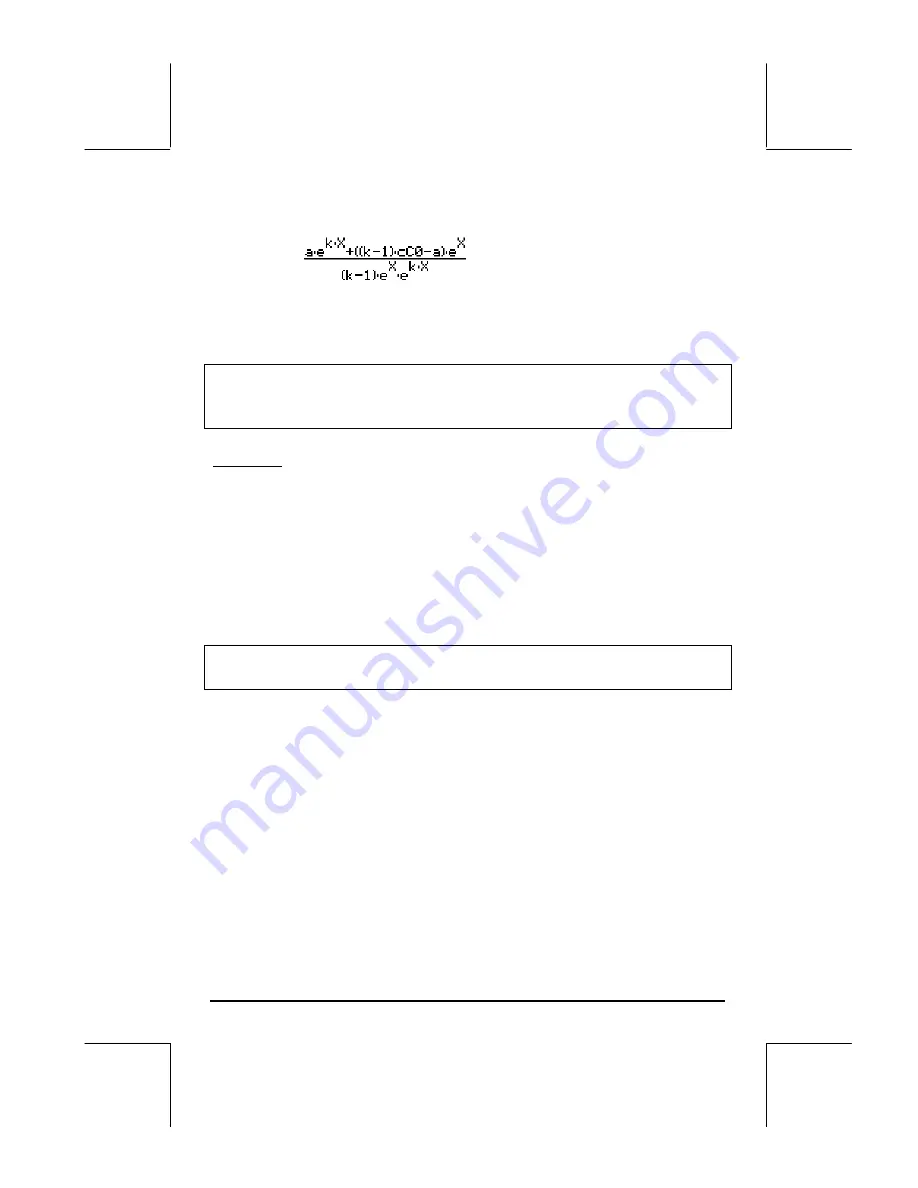
, i.e.,
h(t) = a/(k-1)
⋅
e
-t
+((k-1)
⋅
cC
o
-a)/(k-1)
⋅
e
-kt
.
Thus, cC0 in the results from LDEC represents the initial condition h(0).
Note
: When using the function LDEC to solve a linear ODE of order n in f(X),
the result will be given in terms of n constants cC0, cC1, cC2, …, cC(n-1),
representing the initial conditions f(0), f’(0), f”(0), …, f
(n-1)
(0).
Example 2 – Use Laplace transforms to solve the second-order linear equation,
d
2
y/dt
2
+2y = sin 3t.
Using Laplace transforms, we can write:
L{d
2
y/dt
2
+2y} = L{sin 3t},
L{d
2
y/dt
2
} + 2
⋅
L{y(t)} = L{sin 3t}.
Note
: ‘SIN(3*X)’
`
LAP
µ
produces ‘3/(X^2+9)’, i.e.,
L{sin 3t}=3/(s
2
+9).
With Y(s) = L{y(t)}, and L{d
2
y/dt
2
} = s
2
⋅
Y(s) - s
⋅
y
o
– y
1
, where y
o
= h(0) and y
1
=
h’(0), the transformed equation is
s
2
⋅
Y(s) – s
⋅
y
o
– y
1
+ 2
⋅
Y(s) = 3/(s
2
+9).
Use the calculator to solve for Y(s), by writing:
‘X^2*Y-X*y0-y1+2*Y=3/(X^2+9)’
`
‘Y’ ISOL
The result is
‘Y=((X^2+9)*y1+(y0*X^3+9*y0*X+3))/(X^4+11*X^2+18)’.
















































