Page 18-29
The result indicates that a 95% confidence interval has been calculated. The
Critical z value shown in the screen above corresponds to the values
±
z
α/2
in
the confidence interval formula (
X
−
z
α
/2
⋅σ
/
√
n ,
X+z
α
/2
⋅σ
/
√
n ). The values
µ
Min and
µ
Max are the lower and upper limits of this interval, i.e.,
µ
Min =
X
−
z
α
/2
⋅σ
/
√
n, and
µ
Max =
X+z
α
/2
⋅σ
/
√
n.
Press
@GRAPH
to see a graphical display of the confidence interval information:
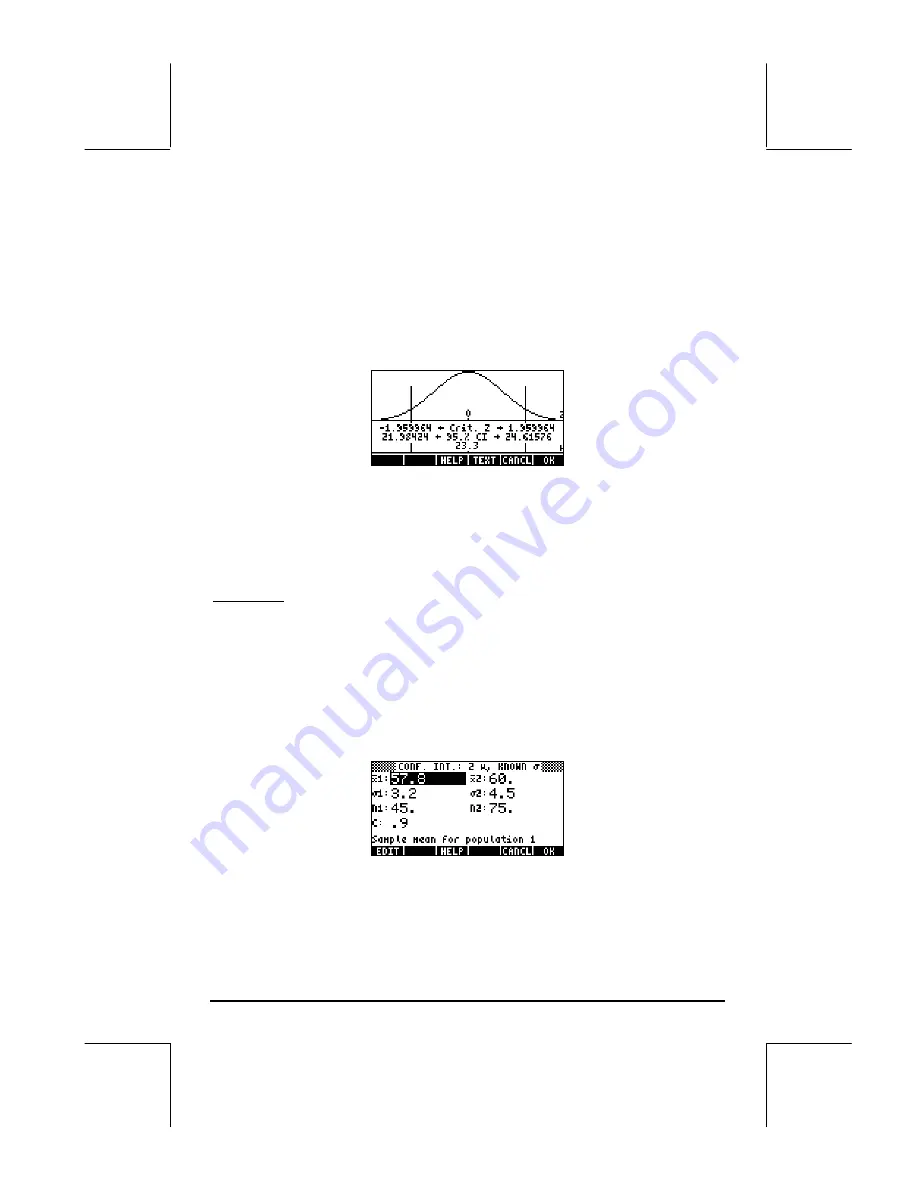
The graph shows the standard normal distribution pdf (probability density
function), the location of the critical points
±
z
α/2
, the mean value (23.2) and
the corresponding interval limits (21.88424 and 24.51576). Press
@TEXT
to
return to the previous results screen, and/or press
@@@OK@@@
to exit the confidence
interval environment. The results will be listed in the calculator’s display.
Example 2 -- Data from two samples (samples 1 and 2) indicate that
x
1
=
57.8 and
x
2
= 60.0. The sample sizes are n
1
= 45 and n
2
= 75. If it is
known that the populations’ standard deviations are
σ
1
= 3.2, and
σ
2
= 4.5,
determine the 90% confidence interval for the difference of the population
means, i.e.,
µ
1
-
µ
2
.
Press
‚Ù—
@@@OK@@@
to access the confidence interval feature in the
calculator. Press
˜
@@@OK@@@
to select option 2. Z-INT:
µ
1 –
µ
2.. Enter the
following values:
When done, press
@@@OK@@@
. The results, as text and graph, are shown below:






























