Page 12-22
{ ‘(X-1)^2+(Y-2)^2=3’ , ‘X^2/4+Y^2/3=1’ }
into the variable EQ.
These equations we recognize as those of a circle centered at (1,2) with
radius
√
3, and of an ellipse centered at (0,0) with semi-axis lengths
a
= 2 and
b
=
√
3.
•
Enter the PLOT environment, by pressing
„ô
, simultaneously if in
RPN mode, and select
Conic
as the
TYPE
. The list of equations will be
listed in the EQ field.
•
Make sure that the independent variable (
Indep
) is set to ‘X’ and the
dependent variable (
Depnd
) to ‘Y’.
•
Press
L
@@@OK@@@
to return to normal calculator display.
•
Enter the PLOT WINDOW environment, by pressing
„ò
,
simultaneously if in RPN mode.
•
Change the range for H-VIEW to -3 to 3, by using
3\
@@@OK@@@
3
@@@OK@@@
. Also, change the V-VIEW range to -1.5 to 2 by
using
1.5\
@@@OK@@@
2
@@@OK@@@
.
•
Change the
Indep Low
: and
High:
fields to Default by using
L
@RESET
while each of those fields is highlighted. Select the option
Reset value
after pressing
@RESET
. Press
@@@OK@@@
to complete the resetting of values.
Press
L
to return to the main menu.
•
Plot the graph:
@ERASE @DRAW
.
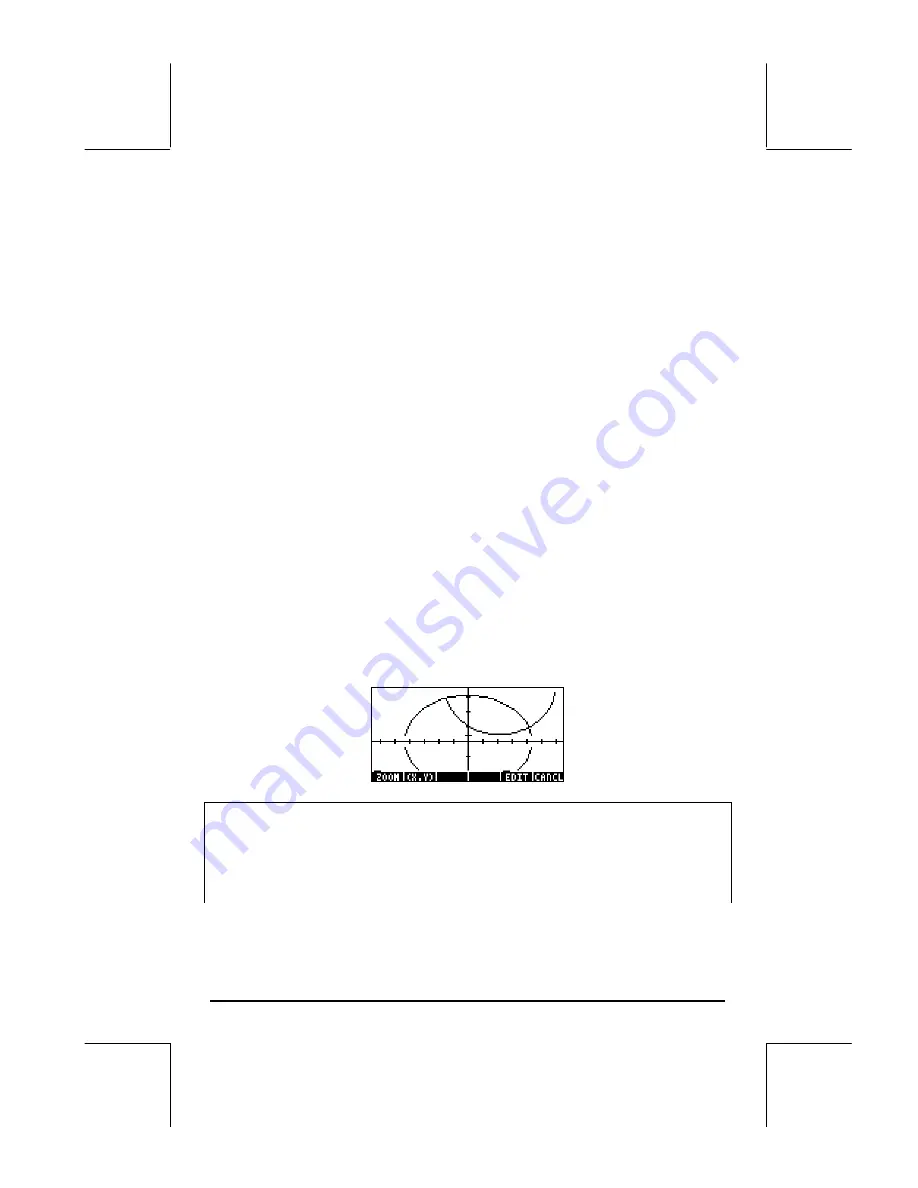
Note
: The
H-View
and
V-View
ranges were selected to show the intersection
of the two curves. There is no general rule to select those ranges, except
based on what we know about the curves. For example, for the equations
shown above, we know that the circle will extend from -3+1 = -2 to 3+1 = 4
in x, and from -3+2=-1 to 3+2=5 in y. In addition, the ellipse, which is






























