Page 14-2
h
y
x
f
y
h
x
f
x
f
h
)
,
(
)
,
(
lim
0
−
+
=
∂
∂
→
.
Similarly,
k
y
x
f
k
y
x
f
y
f
k
)
,
(
)
,
(
lim
0
−
+
=
∂
∂
→
.
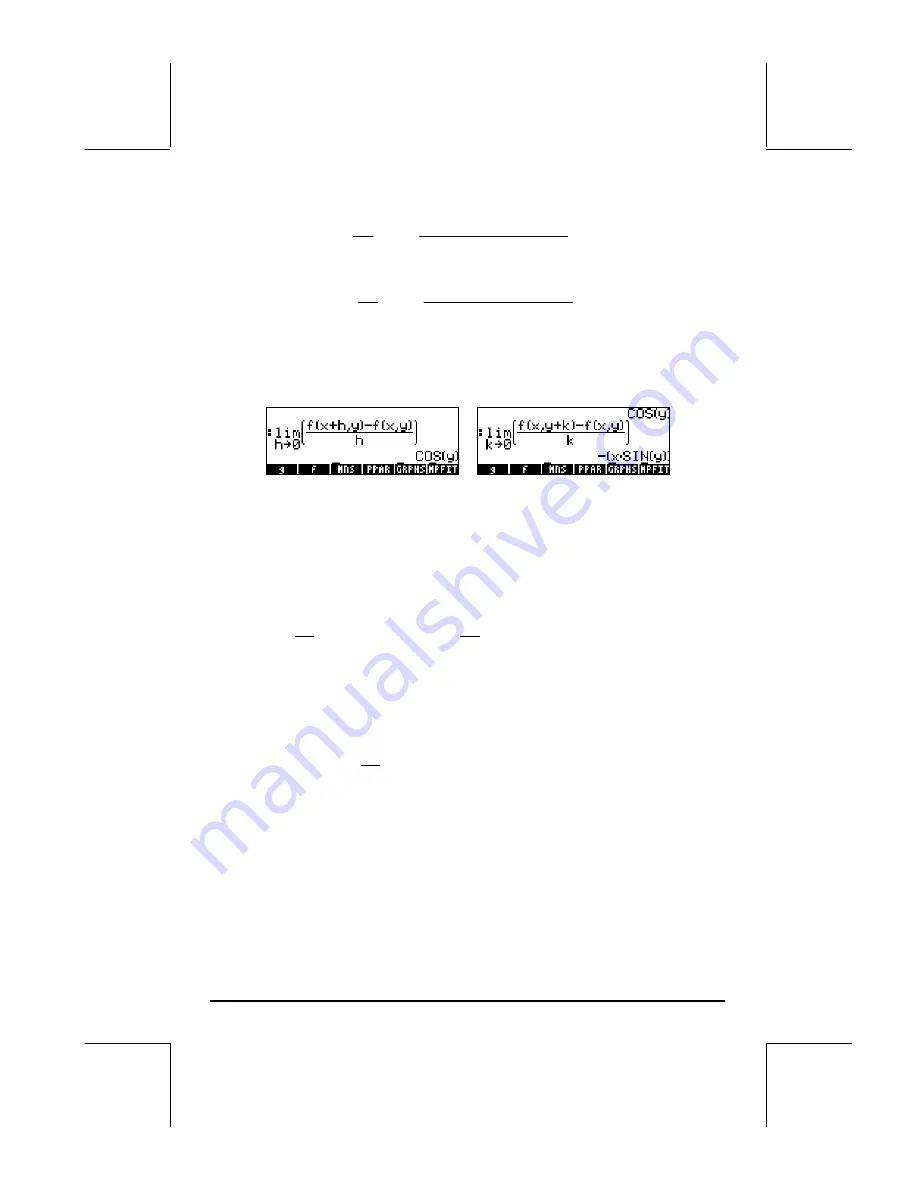
We will use the multi-variate functions defined earlier to calculate partial
derivatives using these definitions. Here are the derivatives of f(x,y) with
respect to x and y, respectively:
Notice that the definition of partial derivative with respect to x, for example,
requires that we keep y fixed while taking the limit as h
0. This suggest a
way to quickly calculate partial derivatives of multi-variate functions: use the
rules of ordinary derivatives with respect to the variable of interest, while
considering all other variables as constant. Thus, for example,
(
)
(
)
)
sin(
)
cos(
),
cos(
)
cos(
y
x
y
x
y
y
y
x
x
−
=
∂
∂
=
∂
∂
,
which are the same results as found with the limits calculated earlier.
Consider another example,
(
)
xy
yx
y
yx
x
2
0
2
2
2
=
+
=
+
∂
∂
In this calculation we treat y as a constant and take derivatives of the
expression with respect to x.
Similarly, you can use the derivative functions in the calculator, e.g., DERVX,
DERIV,
∂
(described in detail in Chapter 13) to calculate partial derivatives.
Recall that function DERVX uses the CAS default variable VX (typically, ‘X’),






























