Page 18-12
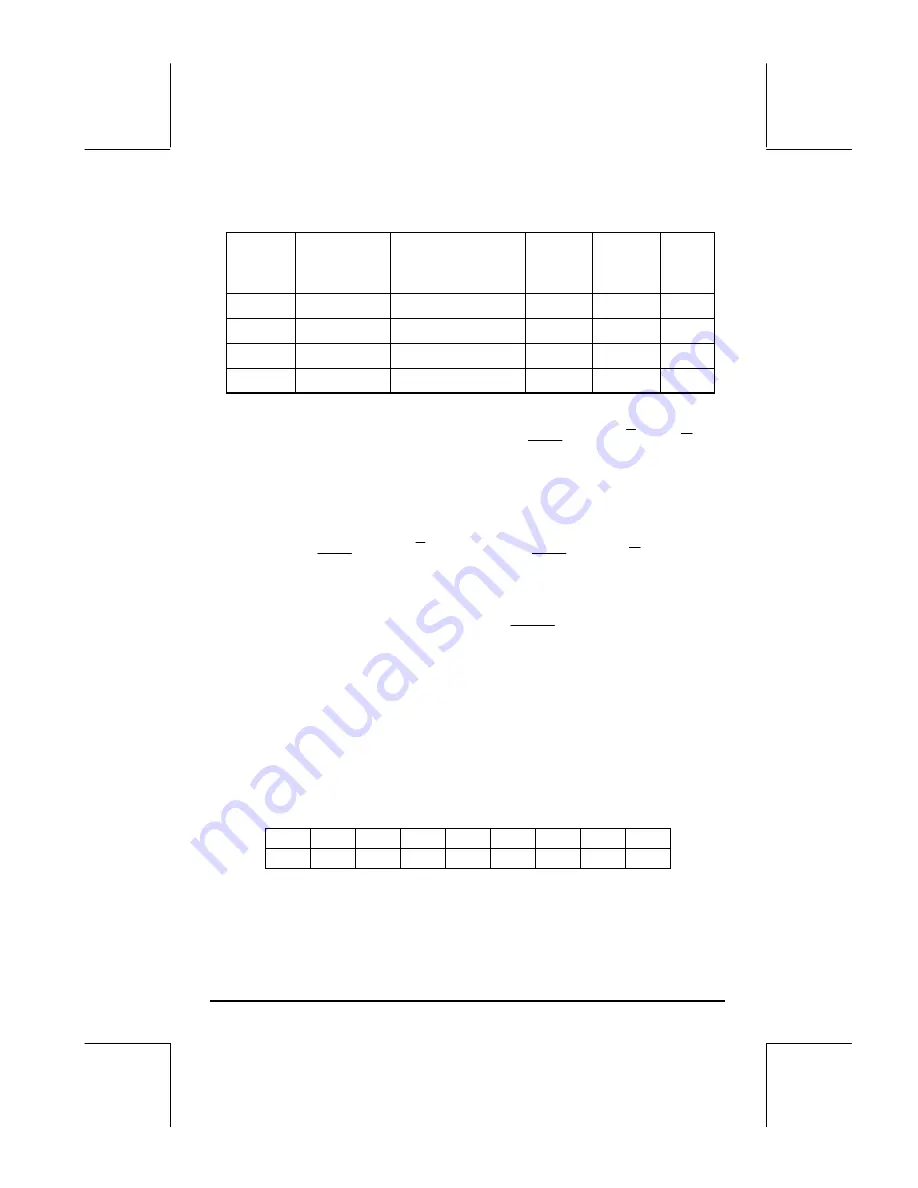
Indep.
Depend.
Type of
Actual
Linearized
variable
Variable Covar.
Fitting Model
Model
ξ η
s
ξη
Linear
y = a + bx
[same]
x
y
s
xy
Log.
y = a + b ln(x)
[same]
ln(x)
y
s
ln(x),y
Exp.
y = a e
bx
ln(y) = ln(a) + bx
x
ln(y)
s
x,ln(y)
Power
y = a x
b
ln(y) = ln(a) + b ln(x)
ln(x)
ln(y)
s
ln(x),ln(y)
The sample covariance of
ξ,η
is given by
)
)(
(
1
1
η
η
ξ
ξ
ξη
−
−
−
=
∑
i
i
n
s
Also, we define the sample variances of
ξ
and
η
, respectively, as
2
1
2
)
(
1
1
ξ
ξ
ξ
−
−
=
∑
=
n
i
i
n
s
2
1
2
)
(
1
1
η
η
η
−
−
=
∑
=
n
i
i
n
s
The sample correlation coefficient r
ξη
is
η
ξ
ξη
ξη
s
s
s
r
⋅
=
The general form of the regression equation is
η
= A + B
ξ
.
Best data fitting
The calculator can determine which one of its linear or linearized relationship
offers the best fitting for a set of (x,y) data points. We will illustrate the use of
this feature with an example. Suppose you want to find which one of the data
fitting functions provides the best fit for the following data:
First, enter the data as a matrix, either by using the Matrix Writer and
entering the data, or by entering two lists of data corresponding to x and y
and using
x 0.2 0.5 1 1.5 2 4 5 10
y 3.16 2.73 2.12 1.65 1.29 0.47 0.29 0.01






























