HD31
- 148 -
V1.6
APPENDIX
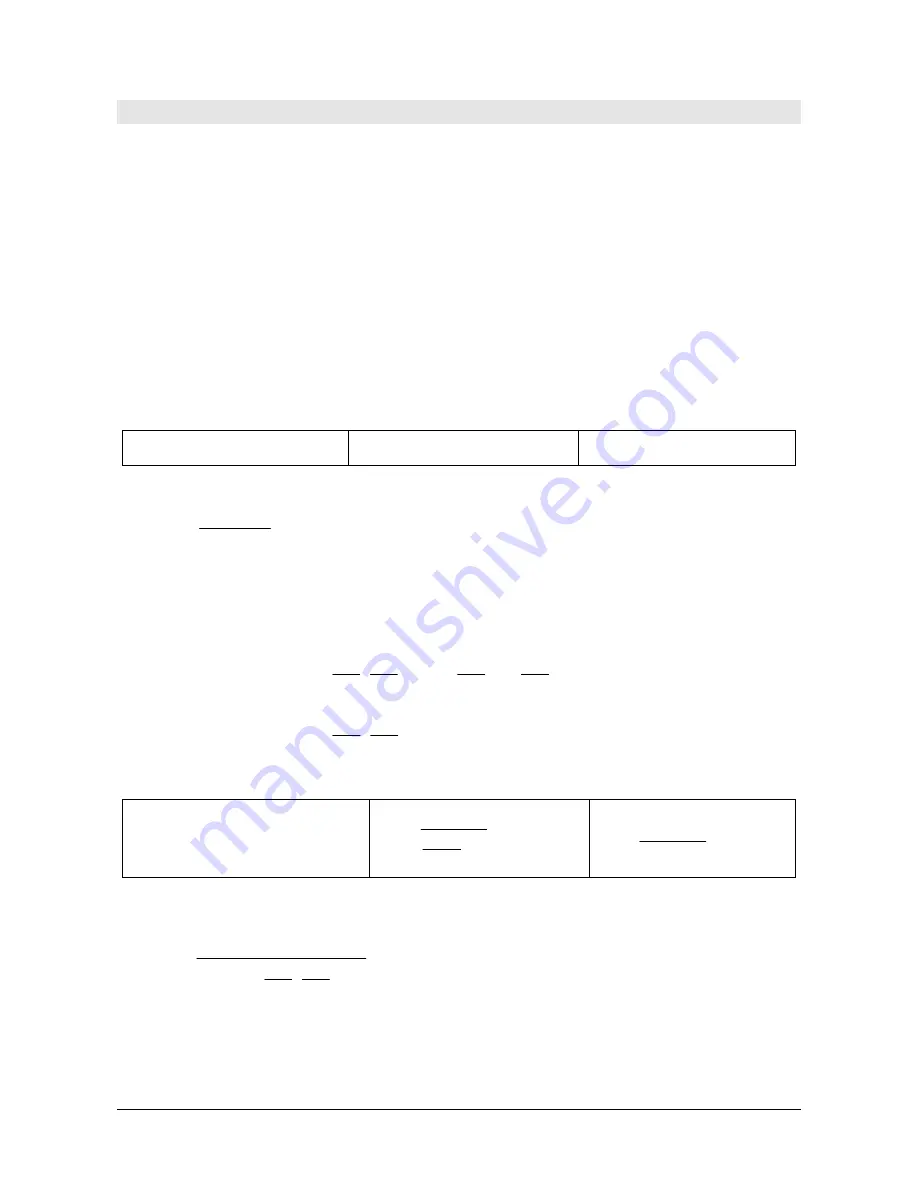
Callendar-Van Dusen equation
The temperature response of a platinum sensor (e.g. Pt100) is described by the equation of
Callendar Van Dusen (1).
(1)
0°C
)
2
1
(
0
)
(
0°C
))
100
(
3
2
1
(
0
)
(
≥
+
+
•
=
<
−
+
+
+
•
=
t
Bt
At
R
t
R
t
t
Ct
Bt
At
R
t
R
The coefficient C is set to 0 for temperatures exceeding zero.
In order to obtain the value of coefficients A, B and C of the equation (1) the probe must be
calibrated in three different points at least. Once known, the coefficients are used to determine
the temperature depending on the resistance value of the sensor.
Coefficients A, B and C for Standard Platinum probes are defined by EN60751 standard:
A
=3.9083 x 10
-3
°C
-1
B
=-5.775 x 10
-7
°C
-2
C
=-4.183 x 10
-12
°C
-4
The temperature coefficient
α
is also defined by the same standard as:
(2)
00385055
0
100
0
0
100
,
=
•
−
=
R
R
R
α
°C
-1
Coefficient
α
can be determined with a calibration operation in 2 points only.
The relationship (1) between the sensor resistance and temperature can be described in an al-
ternative manner by the following equation:
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
•
+
•
=
3
100
1
100
β
1
100
100
δ
1
0
t
t
t
t
t
(t)
α
R
R
0
t
<
°C
(3)
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
•
+
•
=
1
100
100
δ
0
t
t
t
1
(t)
α
R
R
0
t
≥
°C
where:
00385055
.
0
B
100
A
=
+
=
α
°C
-1
499785
.
1
1
B
100
A
100
δ
=
+
−
=
10863
.
0
B
100
A
C
10
β
8
=
+
−
=
The calculation of coefficient
α
between 0 °C and a temperature exceeding 100 °C can be gen-
eralized, by obtaining it from the second of equations (3):
(4)
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
•
−
=
1
100
100
δ
0
0
t
t
t
(t)
R
R
R
α
δ
=
δ
nominal
This allows performing the calibration at 0 °C and in any point provided that it is higher than
100 °C.
Содержание HD31
Страница 6: ...HD31 6 V1 6 2 DESCRIPTION Fig 2 1 instrument description...
Страница 149: ...HD31 149 V1 6 NOTES...
Страница 150: ...HD31 150 V1 6 NOTES...
Страница 151: ......





















