manualshive.com logo in svg

Cleco TME-100, Руководство по программированию, Страница: 100 / 110

Поделиться
Скачать
Cleco TME-100 Скачать руководство пользователя страница 100

100

PL12EN-1300 2008-03

en04d141.fm, 11.03.2008

Statistics

4

7.

Calculate Process Center Lines

After data for 20 samples of five have been plotted, calculate the center lines for both the aver-
age and range plottings.
The center line for the average chart is known as the grand average ( ) and is the average of all 
of the sample averages. This is the value that best represents the size of all measurements:

X

X

n

Σ

where 

Σ

 is used to indicate the sum of the sample averages, ( ), 

(be careful to observe the

 

+ and - signs)

, and n the number of samples, in this case 20.

Similarly, the center line for the range chart ( ) is the average of the ranges for all samples.

R

R

n

Σ

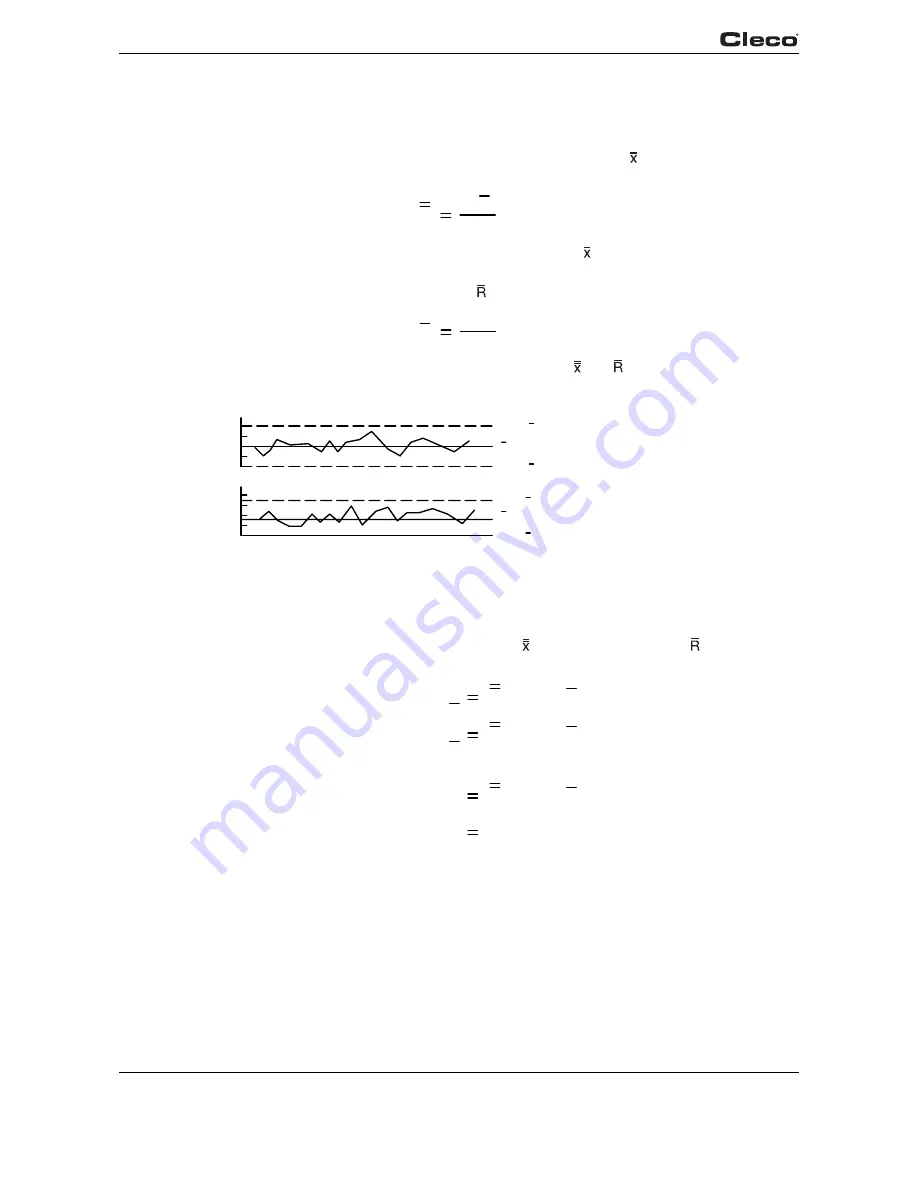
Draw solid lines on the control chart for values representing   and   (see graph 4-4).

R

0

4

8

12

16

20

X

R

X

UCL

X

LCL

UCL

R

LCL

R

ange 

   

   

  A

ve

ra

ge

Fig. 4-4: Drawing The Center Lines And Control Limits

8.

Calculate Control Limits

Calculate the upper and lower control limits (UCL and LCL) using the following formulas and the 
values previously calculated for the grand average ( ) and the average range ( ). 

(Factors are 

for samples of five units only.)

X

x

UCL

+0.577(R)

X

x

LCL

0.577(R)

X

R

UCL

+2.1

14(R) 

0

R

LCL

Average

Range

Note: For a sample size of six or less, the lower control limit for the range is zero.
Plot the limits on the control chart as broken lines.

9.

Evaluate for Statistical Control

Analyze the control chart to see if the process is in a state of statistical control. Variation should 
be random about the center lines for both averages and ranges, with all points within the control 
limits. If these conditions are not satisfied, special cause variation may be present.

Содержание TME-100

Страница 1: ...c Tool Control TME Series Version 2 5 2 Reference Document PL12 1404 Parts manual For additional product information visit our website at http www cooperpowertools com Programming Manual PL12EN 1300 2...

Страница 2: ...damages We likewise do not assume liability for damages resulting from defective circuitry inside the devices supplied Cooper Power Tools reserves the right to ammend supplement or improve this docum...

Страница 3: ...14 2 2 2 Display 14 2 2 3 Keypad Overlay 15 2 2 4 Indicators 15 2 2 5 CPU with PC 104 15 2 2 6 AC Input Power 16 2 2 7 Inernal DC Power 16 2 2 8 Input Output Connectors 16 3 Programming 21 3 1 Naviga...

Страница 4: ...ilder Fieldbus 46 3 4 5 Advanced Linking 51 3 4 6 Advanced Application Builder Signals 52 3 4 7 Advanced Application Builder System Settings 53 3 5 RUN Screen 55 3 5 1 Run Screen Tool 2 57 3 5 2 Run S...

Страница 5: ...ngs 90 3 13 Administration 91 3 13 1 Administration Load Save 91 3 13 2 Administration Print 92 3 13 3 Administration Password 93 3 13 4 Administration Date Time 94 3 13 5 Administration Language 95 3...

Страница 6: ...6 PL12EN 1300 2008 03 PL12EN 1300 TME 200 V2 5 2 0108IVZ fm 11 03 2008...

Страница 7: ...no additional software to begin your fastening process If you are interfacing your unit with an external computer interfacing software is required Contact your distributor for the interfacing software...

Страница 8: ...on the peripheral equipment purchased the unit may be located in a remote position but should still be accessible Attachment of accessories and tools should also be considered with the installation l...

Страница 9: ...d to introduce EMC measures and cover the cost incurred Operation without closed control cabinet is forbidden The properties of the shielding would be altered and the noise emission increase 1 5 Conne...

Страница 10: ...ons may also cause damage to your unit and void exist ing warranties Upon application of power the unit will initiate a self test The initialization takes approximately 45 seconds The introduction scr...

Страница 11: ...s the ship s wheel to return to the Navigator Menu Once Tool Setup is complete the application needs to be programmed To do this go to Basic Application Builder From this screen torque angle and speed...

Страница 12: ...ector Panel Enclosure Key 542818 Indicator Lights Keypad Indicator Lights LCD Display a00254_1 bmp Fig 1 4 Controller 1 1 Tool Connectors Floppy Drive Power In Fuse Holder Ethernet Port Keyboard Port...

Страница 13: ...your unit Soft Keys F1 F4 used to select functions based on the screen displayed ESC Key used at any time to return back one screen or exit the edit mode DEL Key used to delete a numerical value on th...

Страница 14: ...EMA 13 IP54 rating Lockable front door for customer specific key requirements Lockable 3 phase power switch Side door for connector cable protection Removable Mounting Plate Removable fully operationa...

Страница 15: ...w Left Arrow Right Arrow ENTER Enter Orange Border 4 Soft Keys 2 2 4 Indicators 5 Highly visible indicators 2 red groupings 1 green grouping 2 amber groupings Each grouping contains 12 high intensity...

Страница 16: ...kVA peak meets VDA 0570 norm Note If necessary it s possible to connect two units to one 230 VAC power supply with a 16 A slow blow fuse C Type 2 2 7 Inernal DC Power Input 85 VAC 264 VAC Output 5 VD...

Страница 17: ...V 16 Start Switch 0 to 24 V 17 Reverse Switch 0 to 24 V 18 24V 24 V 19 Motor Phase C 0 to 300 V 20 Transducer Calibration 0 to 5 V 21 Temperature Sensor 0 to 5 V 22 Temperature Sensor 0 to 5 V 23 Moto...

Страница 18: ...ata 4 0 to 5 V 7 Data 5 0 to 5 V 8 Data 6 0 to 5 V 9 Data 7 0 to 5 V 10 Acknowledge 0 to 5 V 11 Busy 0 to 5 V 12 Paper Out 0 to 5 V 13 Select Out 0 to 5 V 14 Auto Feed 0 to 5 V 15 Error 0 to 5 V 16 In...

Страница 19: ...8 03 19 Controller Specifications 2 For signal description please see chapter 3 4 2 Advanced Application Builder Inputs page 41 Outputs Pin Description Value 1 24 V Output 24 VDC 2 Output Common Outpu...

Страница 20: ...20 PL12EN 1300 2008 03 en02d141 fm 11 03 2008 Controller Specifications 2...

Страница 21: ...the ESC key The ESC key will return the original value In order to describe the soft key functions the left soft key is referred to as F1 center left soft key F2 center right soft key F3 and right sof...

Страница 22: ...entered it must be entered each time an appropriate screen is exited 3 1 4 Print Screen A Print Screen function is available on all screens In some cases a Print Screen soft key has been added that wi...

Страница 23: ...d Application Builder allows the user to View all Application setups at once and perform I O Mapping The Application Matrix shows an overview of Application and Stage programming by displaying the sel...

Страница 24: ...n load save and configure system information Administration functions include loading and saving the system configuration to a diskette set ting date and time setting password protection and printing...

Страница 25: ...Pressing the Cancel button exits the auto program screen without saving changes Pressing the OK button causes the auto calculations to be done and the results are displayed on the basic screen From th...

Страница 26: ...ram ming the Parameters automatically use the default values 3 2 3 Basic Application Builder Parameters Parameter Name Range Typical Fastening Strategy Torque Control Angle Monitor Angle Control Torqu...

Страница 27: ...and Sequence 41 for all others The automatic selection of a tube nut tool depends on a T in the tool model number That means if a T appears in the model number a tube nut tool is expected This fasten...

Страница 28: ...xits the auto program screen without saving changes Pressing the OK button causes the auto calculations to be done and the results are displayed on the basic screen 3 2 7 Basic Application Builder Cop...

Страница 29: ...ightening in a counter clockwise direction Sequence 41 angle controlled backout and the Backoff Stage are run in the clockwise direction WARNING When the Counter Clockwise box is checked the normal di...

Страница 30: ...py the parameters of an application or stage to one or more other applications or stages by pressing the Copy F2 soft key From this dialog box the user can specify the source and target tool applicati...

Страница 31: ...itor Sequence 50 Angle Control Torque Monitor Sequence 41 Angle Controlled Backoff When a Sequence is selected the Control and Monitor check boxes and Fastening Sequence listbox will both display the...

Страница 32: ...e and Torque Monitoring This tightening sequence is generally preceded by a fast pre tightening cycle The transducer integrated into the nutrunner measures the torque and the resolver measures the ang...

Страница 33: ...the next stage until it reaches the last stage having a selected Sequence It will then rollover to the first stage In order to add a stage without a selected Sequence the user must highlight the stage...

Страница 34: ...and can be output to a printer or transmitted to other sys tem components by data communication When the trigger torque is reached the torque curve is recorded and can be viewed and evaluated using th...

Страница 35: ...e Standard Application Builder Sequence input value 50 Trigger Torque Nm trigger torque beginning of measurement for the graphic display Threshold Torque Nm threshold torque beginning of angle countin...

Страница 36: ...quence 41 Angle Control in Reverse Angle Low Limit Deg 0 to 9999 90 of Turnoff Angle Turnoff Angle Deg Low Limit to 9999 As appropriate Angle High Limit Turnoff angle to 9999 110 of Turnoff Torque Spe...

Страница 37: ...to enter a higher value Relax This sequence is generally used at the end of a rundown to prevent mechanical locking of the tool without loosening the joint The relax parameters are set to values as in...

Страница 38: ...tage until it reaches the last stage with a selected Sequence It will then rollover to the first stage In order to add a stage without a selected Sequence the user must highlight the stage field and e...

Страница 39: ...d in 30 steps to target speed Flex Stop After Turn off Deactivate Flex Stop Allows the user to deactivate the flex stop Flex Stop Percentage of duration of flex stop The higher the percentage the long...

Страница 40: ...Matrix appmatri txtS The Application Matrix is a display matrix of 255 Applications vs 6 Stages showing the selected Sequence number for each stage It gives the user an overview of controller programm...

Страница 41: ...op in Final Stage Tool Start Inputs I0 Application Select 0 I1 Application Select 1 I2 Application Select 2 I3 Tool Start I4 Reject Release I5 Tool Reverse I6 Tool Enable With Linking I7 Reset Linking...

Страница 42: ...actuator on the tool Tool Ready Prepares the controller for a new rundown When active the previ ous outputs are cleared and the yellow LEDs flash Appl Select 0 Application Selects 0 7 are used to sel...

Страница 43: ...previous rundown until cleared by another tool start or the tool ready signal en03d141 fm 11 03 2008 PL12EN 1300 2008 03 43 Programming 3 All inputs are active high They are referenced to an isolated...

Страница 44: ...tage2 c00287en bmp 44 PL12EN 1300 2008 03 en03d141 fm 11 03 2008 Programming 3 Fig 3 15 Output Timing Diagram outputs txtS Eight relay outputs are available at the Phoenix output connector under the r...

Страница 45: ...he tool is running Cycle Complete Active when a rundown has ended in the last stage Linking Complete Active when rundowns of all positions of the selected batch group are complete Linking OK Active if...

Страница 46: ...ication Builder Fieldbus c00400en bmp Fig 3 16 FieldBus fieldbus txtS From the FieldBus Screen the user is allowed to choose from four options for fieldbus connec tions None DeviceNet Profibus or Ethe...

Страница 47: ...bus outputs that replaces the standard Torque Angle results outputs with Cycle OK Cycle NOK and yellow light outputs that originate from tool 2 Dwell Time This is the number of milliseconds that each...

Страница 48: ...Green Tool Light Cycle OK Output data will indicate when cycle is within programmed limits Cycle NOK Output data will indicate when cycle is outside of programmed limits Yellow Tool Light Output data...

Страница 49: ...1 BIT 0 Remote Tool Start BIT1 Remote Tool Reverse BIT 2 Tool Ready Flashing Yellow Light BIT 3 Tool Enable BIT 4 Socket Tray Lamps Enable BIT 5 Socket Tray Lamps Appl Sel 0 BIT 6 Socket Tray Lamps Ap...

Страница 50: ...lect Code 1 8 Mirror BIT 7 Tool Enable from Socket Tray BYTE 1 BIT 0 Tool In Cycle BIT 1 Tool Reverse Switch BIT 2 Fault BIT 3 Cycle Complete BIT 4 Tool Ready pass through from Input BIT 5 Socket Tray...

Страница 51: ...program if the linking strat egy should reset to position 1 after an NOK or set the number of times a fastener can be retight ened after an NOK before advancing to the next position To configure linki...

Страница 52: ...itions that control the activation of sig nals The fault signal for a tool may be activated by a servo warning event total cycles exceeding a desired number cycles since service exceeding a desired nu...

Страница 53: ...lphanumeric This string is appended to the front of default file names so that multiple controller files can be saved to the same disk media Same for both tools 2 Channel only When this box is checked...

Страница 54: ...not reach Turn Off or High Limit torque or angle or reach Max Fastening time In this case an NOK result is generated and the yellow LEDs on the TME and tool will be illuminated Archive only if Torque...

Страница 55: ...ool and Applica tion When allowed the Part ID edit box may be used to manually enter a Part ID using the key pad or an attached keyboard NOTE when manually entering a Part ID the ENTER key must be pre...

Страница 56: ...key displays the Oscilloscope function for evaluating Torque and Angle curves It is automatically updated after each cycle The Run Screen may be optionally configured to display Rundown Details or Co...

Страница 57: ...el V2 xx xx C2 only When tool 2 is selected the run screen display has the labels for the result LEDs on the right side 3 5 2 Run Screen Split Screen c00386en bmp Fig 3 22 Run Screen Split Screen 2 Ch...

Страница 58: ...ng 3 3 5 3 Run Screen TMEI c00413en bmp Fig 3 23 Run Screen Configure The TMEI Run Screen displays an OK or NOK result It does not display a numeric torque value or units The TMEI Run Screen does not...

Страница 59: ...and reset using the Administration Counter screen When the Station Name box is checked and Link ing is disabled the Station Name programmed in Advanced System Settings is displayed next to the applica...

Страница 60: ...om Using the Zoom indicators on the left side of the display a specific area of the torque trace can be enlarged Using the up down arrow keys highlight the Left zoom indicator Using the left right arr...

Страница 61: ...lets you print a hardcopy Note The TMEI does not provide access to the Oscilloscope screen oscope txtE 3 7 Communication 3 7 1 Communications Data Transmission c00404en bmp Fig 3 26 Data Transmission...

Страница 62: ...n Number When the option Advanced System Settings Same for both tools is checked the Tool Number field is hard coded as 01 or 02 as appropriate The following table details the transmission data for St...

Страница 63: ...63 63 1 Char ASCII Status Overall Status Flag A accept R reject 64 65 2 Digit ASCII Link Position Only for Linking 66 67 2 Digit ASCII Number of linked positions Only for Linking 68 68 0D hex CR carr...

Страница 64: ...umber for tool 1 is used For the Rundown packet 4 the Spindle Number field is 1 or 2 depending on the associated tool Refer to Engineering Specification 543027 Network Software Specification for more...

Страница 65: ...d with the rundown data The Part ID is transmitted with the standard serial protocol output data Following either a good rundown linking disabled or good linking sequence linking enabled the Part ID i...

Страница 66: ...urrent values in the edit boxes to be added to the table All values are validated prior to Data Function Allows the tool functionality to be automatically controlled based on the Part ID See Configure...

Страница 67: ...ghtening Group X is selected Ignored when function Tool Enable or Tool Disable is selected comprtid txtE 3 7 3 Communications Printer c00291en bmp Fig 3 28 Printer commprin txtS From this screen the u...

Страница 68: ...screen the user can add IP addresses to the list of remote units To add a remote unit enter the IP address and select Add F1 To delete a remote unit select Delete F2 and enter the position number of...

Страница 69: ...lable or to change the existing tool memory values Pressing the Fixtured Tools F2 key will allow the user to select from a library of predefined fix tured tools This library can be used to program the...

Страница 70: ...2 Tool Library toollib txtS Using the arrow keys move the orange highlight to the desired tool Press ENTER to select that model or ESC to exit If a model is selected these new parameters will be used...

Страница 71: ...e Prev Page F1 and Next Page F2 in order to go through the Chronological History At the top right the Entries XXXX YYYY display indicates the number of Chrono entries matching the filter criteria the...

Страница 72: ...gical History Rundown Information Additional rundown information can be viewed for a rundown by using the up and down arrows to highlight the rundown then press Enter c00414en bmp Fig 3 35 Chronologic...

Страница 73: ...en03d141 fm 11 03 2008 PL12EN 1300 2008 03 73 Programming 3 3 10 2 Statistics Graphs c00357en bmp Fig 3 36 Statistical Histogram c00361en bmp Fig 3 37 Range...

Страница 74: ...ate In Automatic mode the statistics are recalculated and the graph redrawn whenever a new rundown is entered into the Chronological History In Manual mode the recalculation is done only when the user...

Страница 75: ...c00359en bmp Fig 3 39 Chronological History 3 10 3 Statistic Parameter c00401en bmp Fig 3 40 Statistical Parameter statpara txtS From the Parameter Screen the user is able to apply a filter to the chr...

Страница 76: ...Inputs Outputs c00298en bmp Fig 3 41 Inputs Outputs opaldiag txtS A light box for each available input and output is displayed to show the current status In case an input or output is active the ligh...

Страница 77: ...TM COM except for TMEM opaldiag txtE 3 11 2 Diagnostic Fieldbus c00403en bmp Fig 3 42 Fieldbus diafield txtS A light box for each available input and output is displayed to show the current status In...

Страница 78: ...with the values used immediately before the start of a rundown The spindle must be released for this function The values Offset Voltage and Full Scale Voltage of the torque transducer are displayed If...

Страница 79: ...reached during the dwell time if that value is higher than the torque at shut off If the test run is not terminated by a monitoring criterion the total result equals or is higher than 360 degrees and...

Страница 80: ...are the most important supply voltages on the measuring board required for proper torque and angle measurement Therefore these must be monitored continuously If a voltage is out of tolerance it is sho...

Страница 81: ...a rundown The spindle must therefore be released still when this function is called up Then the tool is started at zero speed and the torque is continuously measured and displayed The field Current to...

Страница 82: ...The current output shaft speed is displayed To achieve this the angle factor must have been entered correctly since the integrated speed measurement is derived from the resolver signals When you relea...

Страница 83: ...E 3 11 9 Arcnet Map c00303en bmp Fig 3 49 Arcnet Map arcmap txtS The ARCNET map displays information on the current number of participants in the network their ARCNET ID status serial and software num...

Страница 84: ...on Reconfigurations Change upon each reset of a participant Own reconfigurations Change upon each reset or severe failure Excessive NAK Should be stable New next ID Change upon switch off on of downst...

Страница 85: ...opped synchronous starts CRC error Should be stable Timeout A Should be stable Timeout B Should be stable Wrong ARCNET ID received Should be stable Packets not for host Should be stable ACKs in READY...

Страница 86: ...d or CT01 3964R The Clear Screen F2 soft key will clear the displayed bytes The F3 soft key toggles the transmission record display between ASCII and hexadecimal serial txtE 3 11 12 Event Log c00387en...

Страница 87: ...d141 fm 11 03 2008 PL12EN 1300 2008 03 87 Programming 3 3 12 Utilities 3 12 1 Utilities Installed Versions c00395en bmp Fig 3 53 Installed Versions TME 100 c00396en bmp Fig 3 54 Installed Versions TME...

Страница 88: ...11 03 2008 Programming 3 Fig 3 55 Installed Versions TMEI SWInfo txtS The software and firmware revisions active on the controller are listed on this screen SWInfo txtE 3 12 2 Utilities Software Updat...

Страница 89: ...ntents The storage device may contain many packages for different products but only valid packages intended to be installed on the targeted unit e g TME 200 TMEM are listed The UP and DOWN arrow butto...

Страница 90: ...tem Settings displays the total memory and the available memory of the controller On TME 200 units the screen off timer can be set to the number of minutes the screen backlight will remain activated w...

Страница 91: ...able for TME 100 or TMEM units and therefore is not dis played when connected to either via TM COM or the Cell Manager utilsysset txtE 3 13 Administration 3 13 1 Administration Load Save c00307en bmp...

Страница 92: ...es the user can select the items to print These will be sent to the printer or to a file on the disk media if selected If print to file is checked then the file name is activated to the right and may...

Страница 93: ...meters are changed The Password function sup ports up to ten different users plus a master password Pressing Add User F1 it is possible to add a new user If the first user does not activate the Admini...

Страница 94: ...00310en bmp Fig 3 63 Date Time datetime txtS Using the radio buttons the user can select European or US format for time and date The Checkbox for Winter Summer will account for Daylight Savings Time T...

Страница 95: ...Administration Language c00360en bmp Fig 3 64 Language language txtS The Administration Language screen is used to select the language for the user interface Use the up and down arrow keys to highlig...

Страница 96: ...menu then pressing the Enter key When Backoff is selected the counter is enabled and the current count is decremented each time the tool is started in the backoff direction The Backoff mode is not ava...

Страница 97: ...what the process is doing when to take action and when to leave it alone Although it is a powerful tool the R Control Chart is easy to use Only an understanding of a few basic statistical concepts an...

Страница 98: ...ese two characteristics the average and the standard deviation provide the foundation for statistical process control By taking sample measurements during production we can predict the average value a...

Страница 99: ...equip ment must be of a type suitable for the characteristic being evaluated and must be calibrated and properly used Decisions resulting from the analysis of a control chart will be no better than t...

Страница 100: ...nting and see graph 4 4 R 0 4 8 12 16 20 X R X UCL X LCL UCL R LCL Range Average Fig 4 4 Drawing The Center Lines And Control Limits 8 Calculate Control Limits Calculate the upper and lower control li...

Страница 101: ...e to center the process so that the process average is close to the middle of the specification tolerance This can usually be accomplished by a simple machine or tooling adjustment If the magnitude of...

Страница 102: ...lly the first since it has a direct impact on customer satisfaction The six sigma spread of the process described in this procedure is in general use throughout American industry When properly applied...

Страница 103: ...2EN 1300 2008 03 103 Statistics 4 mean or average R range Cp Capability of Process Cpk Capability index n number of runs Sub Sz Subgroup size Y Torque summary run data A Angle summary run data Note Se...

Страница 104: ...104 PL12EN 1300 2008 03 en04d141 fm 11 03 2008 Statistics 4...

Страница 105: ...roduct group application select 0 2 application selects 0 2 are used to select applications 1 8 using a binary count of 0 7 where app sel 0 is the least significant bit baud rate the frequency at whic...

Страница 106: ...ata from a run cycle linking Allows the user to automatically change from application to application for a predefined number of positions up to 32 Up to eight different linking strategies called Tight...

Страница 107: ...referred to as the redundant transducer sequence 11 high speed rundown sequence 30 torque control angle monitor sequence 50 angle control torque monitor sequence 41 angle controlled backoff speed max...

Страница 108: ...torque high active of peak torque torque high limit torque high limit THL the maximum acceptable torque value for one cycle torque low active if peak torque torque low limit torque low limit TLL the m...

Страница 109: ......

Страница 110: ...l Iporanga 18087 170 Sorocaba SP Brazil Tel 55 15 3238 3929 Fax 55 15 228 3260 Cooper Power Tools 4121 North Atlantic Blvd Auburn Hills MI 48326 USA Tel 248 391 3700 Fax 248 391 6295 Sales Service Cen...

Отзывы:

Нет отзывов