Kurzweil K2500RS, Musician'S Manual

Page: 349 / 530

FUNS
The FUN Equations
16-7
.5625 .625 10 5*
.625 .6875 11 6
.6875 .75 12 6*
.75 .8125 13 7
.8125 .875 14 7*
.875 .9375 15 8
.9375 1 16 8*
As an example, consider the FUN we set up at the beginning of the previous section: the Mod
Wheel was assigned as
input a , and the data slider as input b . The FUN was assigned as Src1
on the PITCH page, and the depth of Src1 was set to 1200 cents. If you push the Mod Wheel all
the way up, the value of
input a will be +1. This will set the number of steps at 8, since the data
slider sends a unipolar control signal. With your MIDI controllerÕs data slider at minimum,
play and sustain a note. Then move the data slider slowly up. The pitch of the note will jump
up an octave in 8 steps as you move the data slider all the way up.
If the value of input a is negative, itÕs multiplied by -1, so its value always falls within the
ranges above. When input b is bipolar and the resulting number of steps is an odd number, the
steps are centered around a value of 0Ñthat is, the center step is equivalent to no effect from
input b . When the number of steps is even, a value of zero is not included in the steps. This is
also true for the values marked by an asterisk when input b is unipolar.
lowpass (f = a, b)
This equation might be called a lag equation. Its effect is to introduce a delay in the K2vxÕs
response to changes in the value of
input b . It works by Þltering (reducing) higher values of
input b . The value of input a determines the degree to which the values of input b are Þltered.
Low values for input a will induce a long lag when the value of input b changes. High values
will shorten the lag. When input b remains constant at a high level, low values of input a will
cause the FUN to sweep up slowly from 0 to the value of input b . Higher values for input a will
cause the FUN to sweep more rapidly.
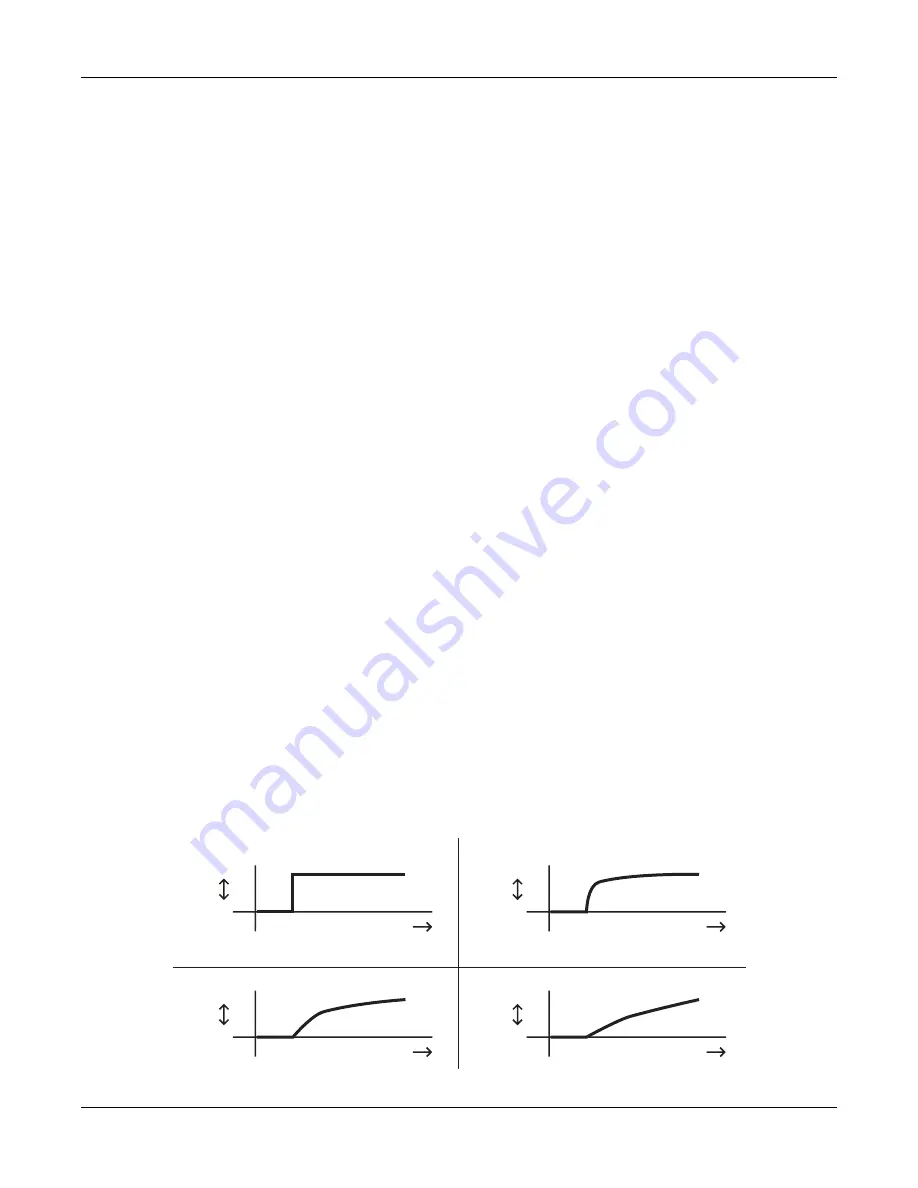
The four graphs below show the effect of different values for input a on the change of input b .
In each graph, the value of input b jumps from 0 to +1. In graph 1, the value of input a is +1.
Each successive graph represents the same change in the value of input b , at successively lower
values for input a .
This equation works as intended only when the value of input a is 0 or positive. Negative
values for input a will result in a much less predictable response than positive values. You
might like the effect, but it wonÕt be anything like what weÕve just described.
input b
value
time
input b
value
time
input b
value
time
input b
value
time
1)
4) 3)
2)