ST2516 Series Operation Manual
20
NOTE: Before measurement, it is necessary to warm up the instrument and the probe for about
half an hour. The temperature sensor should be placed to the DUT as close as possible but
cannot contact it. After the displayed result comes to be stable, you can read or record the
result.
3.6.2
Temperature conversion (∆t)
Temperature conversion (∆t)
: Basically, resistors have heat effect. Temperature conversion
represents the temperature difference between the resistor and the environment.
Formula:
2 (
1) (
)
1
R
t
k t
k ta
R
∆ =
+
−
+
∆
t is the temperature increment.
t1 is the temperature at the start of resistance measurement.
ta is the environment temperature.
R1 is the resistance at the start of contact.
R2 is the resistance after the display is stable.
K is the variance ration of the environment temperature coefficient when the conductor is at
0
℃
.
For example
When R1 is 2
00mΩ,
t1 is 20
℃, R2 is
210
mΩ, ta is 25
℃ and k is 235.
Δ
t
=
𝐑𝟐
𝐑𝟏
(k + t1) –(k + ta)=
𝟐𝟏𝟎
𝐱𝟏𝟎
−𝟑
𝟐𝟎𝟎
𝐱𝟏𝟎
−𝟑
(235 + 20) –(235+25)=7.75
℃
The temperature after the resistance is stable is calculated as the following formula:
𝑡
𝑅
=
ta +Δt = 25 +7.75 = 32.75
℃
Where, k =
1
α
t0
- t0, if
α
t0
= 3930ppm, k is 234.5
NOTE: Conductivity and temperature coefficient of metal and alloy
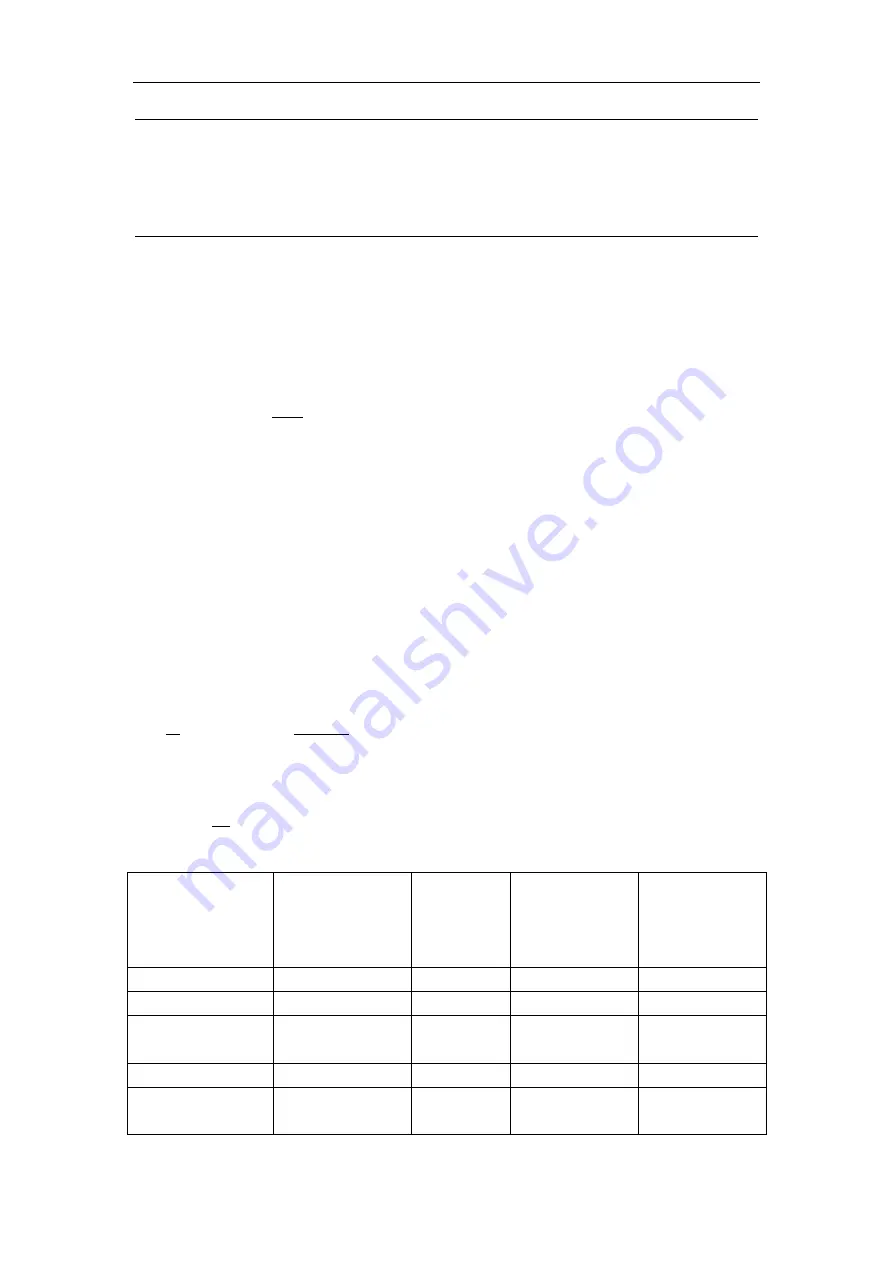
Metallic material
Metal
[%]
Material
density
(x
10
3
)
[kg/
m
3
]
Conductivity
Temperature
coefficient
(20
℃
)
[ppm]
Annealed copper
Copper>99.9
8.89
1.00 to 1.02
3810 to 3970
Hard-drawn copper Copper>99.9
8.89
0.96 to 0.98
3370 to 3850
Cadmium copper
Cadmium: 0.7 to
1.2
8.94
0.85 to 0.88
3340 to 3460
Silver copper
Silver: 0.03 to 0.1
8.89
0.96 to 0.98
3930
Chromium copper
Chromium: 0.4 to
0.8
8.89
0.40 to 0.50
0.80 to 0.85
20
30






























