Parker Compax3S025V2, Руководство по эксплуатации

Страница: 227 / 314

Parker EME
Setting up Compax3
192-120101 N11 C3I11T11 November 2007
227
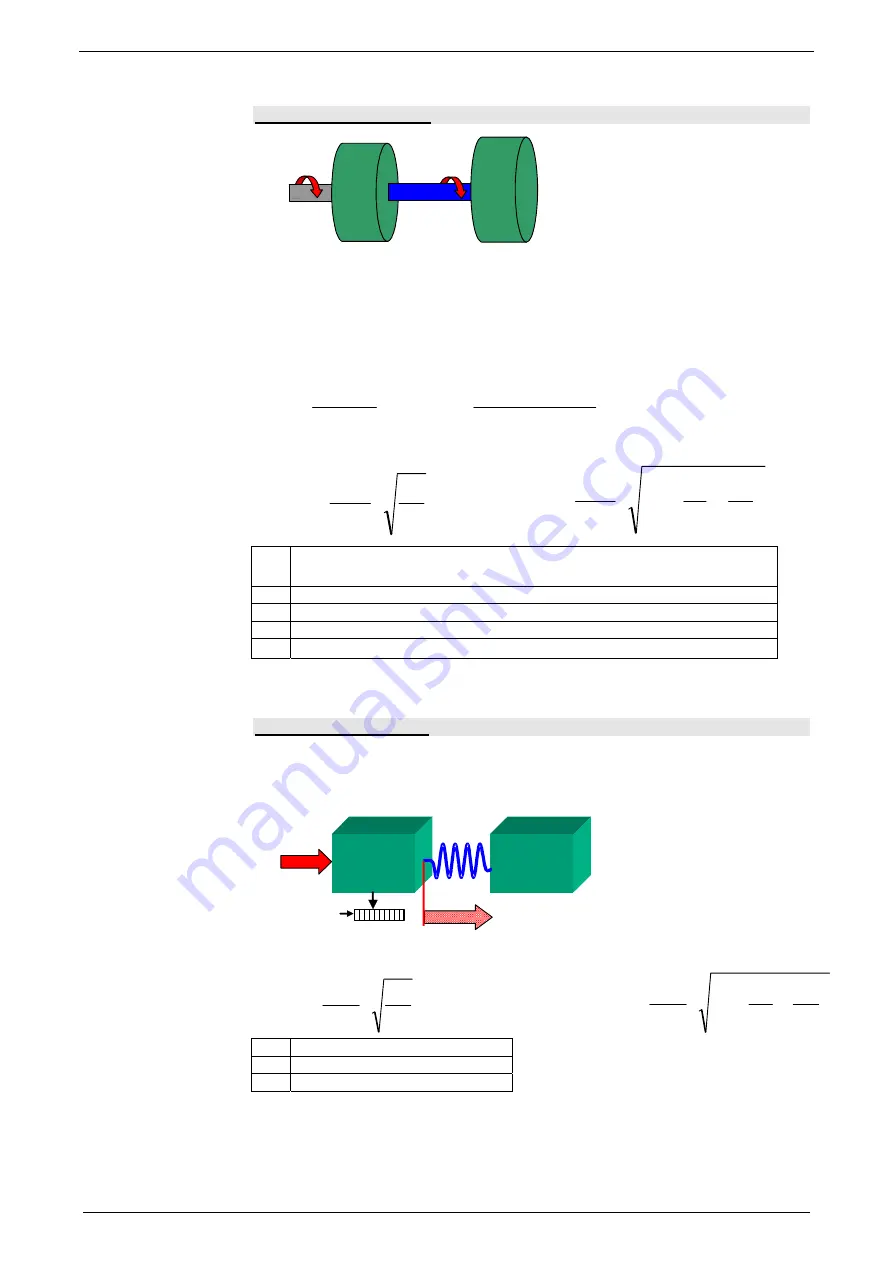
Rotary two mass system
M
M
1
1
M
M
2
2
J
J
1
1
J
J
2
2
D
D
The shown system corresponds for instance to a motor with a flywheel coupled via
a shaft. Hereby J1 corresponds to the motor moment of inertia and J2 to the
moment of inertia of the flywheel.
Calculation of the resonance frequencies in the rotary system with a hollow
shaft as elastic coupling element
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+ ⋅ ⋅
⋅
=
2 1
Re
1 1
2
1
J J
D f
s
π
2
Re
2
1
J
D
f
s A
⋅
⋅
=
π
( )
l
r r G
dr r
l
G
D
I A
r
r
A
I
⋅
− ⋅ ⋅
= ⋅ ⋅
⋅ ⋅
=
∫
2
2
4 4
3
π π
G Shear modulus of the material used [N/m²]
(e.g. approx. 80750N/mm² for steel)
D Torsional rigidity in [m/rad]
rA Outer radius of the hollow shaft
rI Inner radius of the hollow shaft
l Length of the hollow shaft
Linear two mass system
M1 M2
F
F
1
1
D
D
F
F
2
2
Feedback
Resonance frequencies in the linear system
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+ ⋅ ⋅
⋅
=
2 1
Re
1 1
2
1
m m
D f
s
π
2
Re
2
1
m
D
f
s A
⋅
⋅
=
π
D Rigidity in [N/m]
m1 e.g. motor mass
m2 e.g. load mass