manualshive.com logo in svg

Casio FX-CG10, User Manual

Share
Download
Casio FX-CG10 User Manual Download Page 273

6-71

k

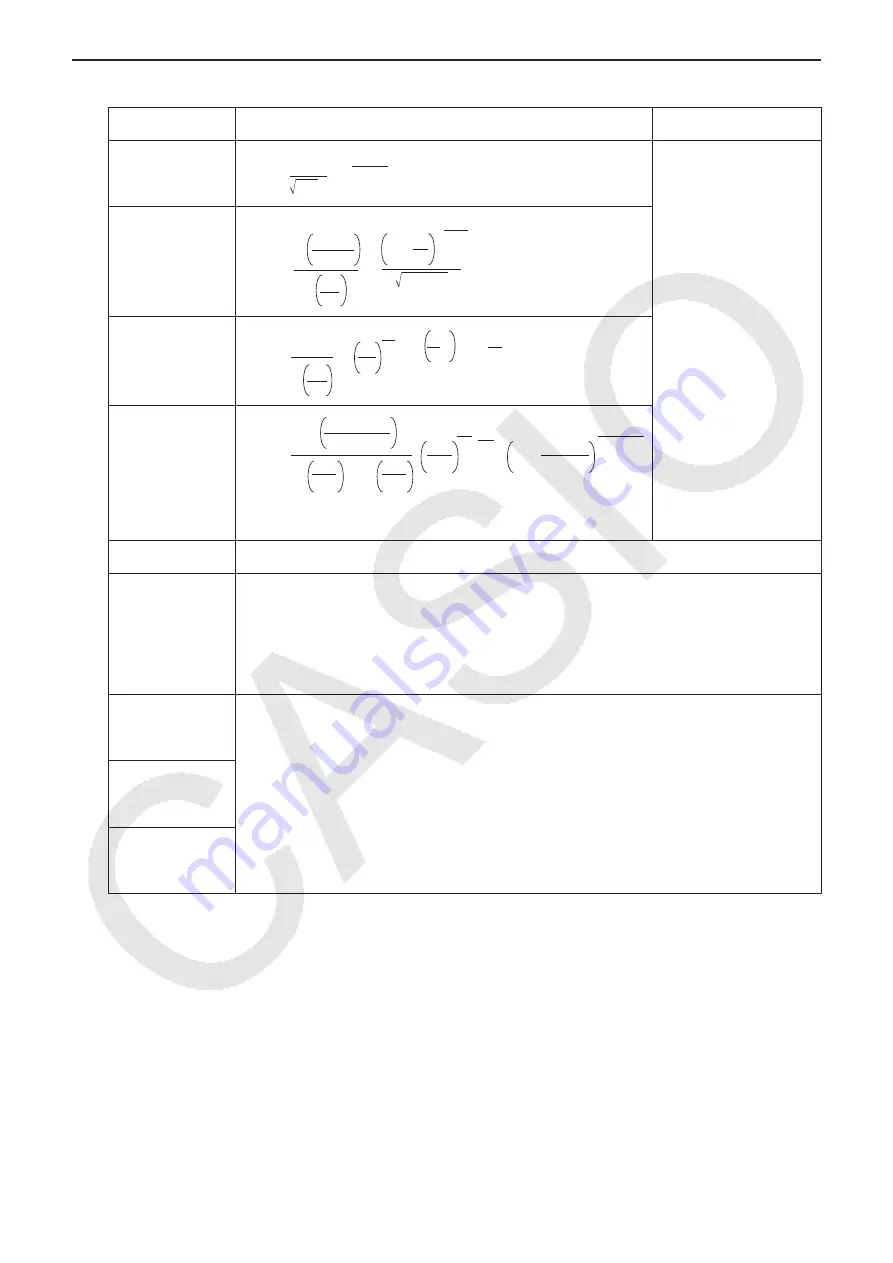
 Distribution (Continuous)

  Distribution  

  Probability Density  

  Cumulative Distribution  

 Normal 
Distribution 

  

πσ

2

p

(

x

) = 

1

e

–

2  

2

σ

(

x

 

– 

μ

)

2

μ

(

   

> 0)

σ

  

  

p

 = 

p

(

x

)

dx

 

Upper

Lower

∫

  

 Student- 

t 

 

Distribution 

 

p

(

x

) = 

×

Γ

Γ

 

×

 df

π

–

 df

+

1

2

2

df

2

df

 

+ 1

df

x

2

1 +

 

  χ  

2 

 Distribution 

 

p

(

x

) = 

×

(

x

 

 0)

Γ

1

2

df

df

2

 

×

 x           

2

1

df

2

–

1

x

2

–

 ×

 e

 

  F 

 Distribution 

 

ndf

2

x

ddf

ndf

ndf

2

–

1

ddf

ndf 

×

 x

1 +

ndf + ddf

2

p

(

x

) = 

–

Γ

2

ndf 

+ 

ddf

Γ

2

ndf

 × Γ

2

ddf

(

x

 

 0)

 

  Distribution   

  Inverse Cumulative Distribution  

 Normal 
Distribution 

  

p

 = 

p

(

x

)

dx

 

Upper

–

∞

∫

 

p

 = 

p

(

x

)

dx

 

Lower

∞

∫

 

p

 = 

p

(

x

)

dx

 

Upper

Lower

∫

   

 

tail = Left 

 

tail = Right 

 

tail = Central 

 Student- 

t 

 

Distribution 

 

p

 = 

p

(

x

)

dx

 

Lower

∞

∫

 

  χ  

2 

 Distribution 

  F 

 Distribution 

Summary of Contents for FX-CG10

Page 1: ...CASIO Worldwide Education Website http edu casio com Manuals are available in multi languages at http world casio com manual calc fx CG10 fx CG20 fx CG20 AU Software Version 2 02 User s Guide E...

Page 2: ...s guide are subject to change without notice No part of this user s guide may be reproduced in any form without the express written consent of the manufacturer Be sure to keep all user documentation...

Page 3: ...culations with Integers 2 39 8 Matrix Calculations 2 42 9 Vector Calculations 2 59 10 Metric Conversion Calculations 2 64 Chapter 3 List Function 1 Inputting and Editing a List 3 1 2 Manipulating List...

Page 4: ...Cost Selling Price Margin 7 13 8 Day Date Calculations 7 14 9 Depreciation 7 15 10 Bond Calculations 7 17 11 Financial Calculations Using Functions 7 20 Chapter 8 Programming 1 Basic Programming Step...

Page 5: ...n Image 14 37 5 Using the Measurement Box 14 41 6 Working with Animations 14 56 Chapter 15 Picture Plot 1 Picture Plot Function Menus 15 3 2 Managing Picture Plot Files 15 5 3 Using the Plot Function...

Page 6: ...e Math input output mode see Using the Math Input Output Mode page 1 13 u x The above indicates you should press and then x which will input a symbol All multiple key input operations are indicated li...

Page 7: ...Adjust the brightness The e cursor key makes display brightness lighter The d cursor key makes display brightness darker 1 INITIAL returns display brightness to its initial default 3 To exit display b...

Page 8: ...ing the Examination Mode Input Output Frac Result Angle Complex Mode Display Q1Q3 Type Language Function menu language Battery Type u Calculator Operation in the Examination Mode Entering the Examinat...

Page 9: ...power off and then back on again Yes Yes Press the RESTART button Yes No Remove the calculator s batteries Yes No Delete Main Memory data Yes No u Exiting the Examination Mode There are three ways to...

Page 10: ...he Examination Mode Calculator B 3 On Calculator A press 2 RECV 4 On Calculator B enter the Link mode and then press 3 EXAM 1 UNLOCK 1 Yes You could also transfer any data from Calculator B to Calcula...

Page 11: ...8 2 1 2 1 2 11 2 1 1 7 1 17 2 1 1 12 2 16 2 9 1 11 5 4 5 15 2 49 1 36 1 12 3 3 2 36 10 21 10 19 2 16 1 2 2 16 1 16 1 28 1 3 Page Page Page Page Page Page Page Page Page Page Page 2 1 1 31 1 32 1 2 2 1...

Page 12: ...3 B al The following describes the color coding used for key markings Color Key Operation Yellow Press and then the key to perform the marked function Red Press a and then the key to perform the mark...

Page 13: ...riable standard deviation and paired variable regression statistical calculations to perform tests to analyze data and to draw statistical graphs eActivity eActivity lets you input text math expressio...

Page 14: ...e to control the optionally available Data Logger Link Use this mode to transfer memory contents or back up data to another unit or PC Memory Use this mode to manage data stored in memory System Use t...

Page 15: ...l 1 icon appears immediately replace the batteries For details about battery replacement see the separate Hardware User s Guide Calculation in progress key was pressed and the calculator is standing b...

Page 16: ...ormat 1 2E 12 indicates that the result is equivalent to 1 2 1012 This means that you should move the decimal point in 1 2 twelve places to the right because the exponent is positive This results in t...

Page 17: ...t input your calculation formulas exactly as they are written from left to right and press w to obtain the result Example 2 3 4 10 Ac d e baw k Editing Calculations Use the d and e keys to move the cu...

Page 18: ...theses are color coded during input and editing of calculation formulas in order to make it easier to confirm the proper relationship between opening and closing parentheses The following rules are ap...

Page 19: ...he contents of the replay memory by pressing d or e If you press e the calculation appears with the cursor at the beginning Pressing d causes the calculation to appear with the cursor at the end You c...

Page 20: ...One calculation back f Two calculations back A calculation remains stored in replay memory until you perform another calculation The contents of replay memory are not cleared when you press the A key...

Page 21: ...then press i CLIP This will cause to appear in the status bar 2 Use the cursor keys to move the cursor and highlight the range of text you want to copy 3 Press 1 COPY to copy the highlighted text to t...

Page 22: ...ds The screen that appears first is the last one you used for command input 2 Press 6 CAT to display the category list You can skip this step and go straight to step 5 if you want 3 Use the cursor key...

Page 23: ...forms a completely different function in the Math input output mode For more information see Using Values and Expressions as Arguments page 1 17 Unless specifically stated otherwise all operations in...

Page 24: ...is is the number of bytes for a 2 2 matrix u Using the MATH Menu In the Run Matrix mode pressing 4 MATH displays the MATH menu You can use this menu for natural input of matrices derivatives integrals...

Page 25: ...erent examples showing how the MATH function menu and other keys can be used during Math input output mode natural input Be sure to pay attention to the input cursor position as you input values and d...

Page 26: ...1 16 Example 3 To input 1 x 1dx 0 1 Ab 4 MATH 6 g 1 dx v b ea fb e w Example 4 To input 2 1 2 2 1 2 2 Ac 4 MATH 1 MAT VCT 1 2 2 vbcc ee x ce e x ceevbcc w...

Page 27: ...Expressions as Arguments A value or an expression that you have already input can be used as the argument of a function After you have input 2 3 for example you can make it the argument of resulting...

Page 28: ...re information u Editing Calculations in the Math Input Output Mode The procedures for editing calculations in the Math input output mode are basically the same as those for the Linear input output mo...

Page 29: ...ration you have just undone To undo the last key operation press aD UNDO To redo a key operation you have just undone press aD UNDO again You also can use UNDO to cancel an A key operation After press...

Page 30: ...s the same screen used in the Linear input output mode Lists are displayed in natural format for up to 20 elements A list that has more than 20 elements will be displayed on a ListAns screen which is...

Page 31: ...ts are contained in history by checking the length of the scroll bar A shorter bar indicates a greater number of entries The value stored in the answer memory is always dependent on the result produce...

Page 32: ...Input Output Mode Example Operation 4 5 6 10 3 3 2 1 cos Angle Rad log28 3 123 1 988647795 7 2 3 3 64 4 10 A6v4 5w Ac E v3e w A4 MATH 2 logab 2e8w A M x 7e123w A2 3 M x 3e64e 4w 4 3 0 1249387366 log A...

Page 33: ...H to display the MATH menu 3 Press 1 MAT VCT to display the following menu 2 2 inputs a 2 2 matrix 3 3 inputs a 3 3 matrix m n inputs an m row n column matrix or vector up to 6 6 2 1 inputs a 2 1 vect...

Page 34: ...evious page bebvceedde bdveeefege iw u To assign a matrix created using Math input output mode to a specified matrix memory Example To assign the calculation result to Mat J c Mat Ans a c Mat a J w Pr...

Page 35: ...Equation mode See the sections that cover each calculation for details about its operation See Input Operations in the Math Input Output Mode page 1 13 and Calculation Operations in the Math Input Ou...

Page 36: ...use the Math input output mode in the Equation mode for input and display as shown below In the case of simultaneous equations 1 SIMUL and high order equations 2 POLY solutions are output in natural...

Page 37: ...LIST list function menu MAT VCT matrix vector operation menu COMPLEX complex number calculation menu CALC functional analysis menu STAT menu for paired variable statistical estimated value distributi...

Page 38: ...value indicates the display range Xmax value Xmin value divided by the screen dot pitch The dot value is normally calculated automatically from the minimum and maximum values Changing the dot value c...

Page 39: ...m error sum of squares error mean squares INTR confidence interval calculation results Lower Upper p p1 p2 df confidence interval lower limit confidence interval upper limit estimated sample proportio...

Page 40: ...Matrix and Program modes 3 Table contents are stored automatically in Matrix Answer Memory MatAns u EQUATION Recalling equation coefficients and solutions 1 2 SimRes SimCoef matrix of solutions 3 coe...

Page 41: ...and output command CLEAR clear command menu DISPLAY display command menu RELATNL conditional jump relational operator menu I O I O control transfer command menu multi statement command STR string comm...

Page 42: ...ys to move the highlighting to the item whose setting you want to change 4 Press the function key 1 to 6 that is marked with the setting you want to make 5 After you are finished making any changes yo...

Page 43: ...real number range only a bi r rectangular format polar format display of a complex calculation u Coord graph pointer coordinate display On Off display on display off u Grid graph gridline display On O...

Page 44: ...rea numeric sequence u Background background image display None PICT n OPEN no background specify picture memory image as the background specify an image as the background u Plot LineCol plot and line...

Page 45: ...display display without reduction u Q1Q3 Type Q1 Q3 calculation formulas Std OnData divide total population on its center point between upper and lower groups with the median of the lower group Q1 and...

Page 46: ...image of a message indicating that an operation or data communication is in progress A Memory ERROR will occur if there is not enough room in main memory to store the screen capture u To recall a scre...

Page 47: ...however that you should only use the RESTART button only as a last resort Normally pressing the RESTART button reboots the calculator s operating system so programs graph functions and other data in...

Page 48: ...e danger that memory contents will be corrupted or lost entirely You will not be able to perform data communication operations after the low battery message appears k Image File Compatibility An image...

Page 49: ...tivity files that contain inserted images that were stored or updated on the fx CG20 fx CG20 AU cannot be opened with the fx CG10 If the message Provided by CASIO appears at the bottom of the detail s...

Page 50: ...utput mode 6 4 5 w 1 Final closed parentheses immediately before operation of the w key may be omitted no matter how many are required k Number of Decimal Places Number of Significant Digits Normal Di...

Page 51: ...w 14w 28 571 Ans I 400 000 If the same calculation is performed using the specified number of digits 200 7w 28 571 The value stored internally is rounded off to the number of decimal places specified...

Page 52: ...ns the function key is pressed and then the value is entered 3 log ln ex 10x sin cos tan sin 1 cos 1 tan 1 sinh cosh tanh sinh 1 cosh 1 tanh 1 d h b o Neg Not Det Trn Dim Identity Ref Rref Sum Prod Cu...

Page 53: ...on the Setup screen Example 2 8 3 2 Input Output Math x ce x iw u Calculation Result Display Range with Display of a calculation result in format is supported for result with in up to two terms Calcu...

Page 54: ...4 2 6 8 898979486 If the calculation formula has a term and a term that cannot be displayed as a fraction the calculation result will be displayed in decimal format Example log3 2 1 891334817 u Calcu...

Page 55: ...ge 2 3 and Type C functions 6 on page 2 3 except for negative signs Example 1 2sin30 10log1 2 2 3 2Pol 5 12 etc Before constants variable names memory names Example 2 2 2AB 3Ans 3Y1 etc Before an open...

Page 56: ...quire one byte are b c d sin cos tan log ln and Some of the functions that take up two bytes are d dx Mat Vct Xmin If For Return DrawGraph SortA PxIOn Sum and an 1 The required number of bytes to inpu...

Page 57: ...and then assign 5 to X Next check what is assigned to x Abaavw faa X w vw u To assign the same value to more than one variable value a first variable name last variable name w You cannot use r or as a...

Page 58: ...nd that you use the Graph mode for expressions and the Program mode for programs STORE RECALL fn SEE function store function recall function area specification as a variable name inside an expression...

Page 59: ...he display u To recall a function as a variable Adaav A w baal B w K6 g 6 g 3 FUNCMEM 3 fn b cw u To display a list of available functions K6 g 6 g 3 FUNCMEM 4 SEE u To delete a function Example To de...

Page 60: ...ch power off u To use the contents of the answer memory in a calculation Example 123 456 579 789 579 210 Abcd efgw hij Ans w Performing an operation that assigns a value to an Alpha memory such as faa...

Page 61: ...elow 360 2 radians 400 grads 90 2 radians 100 grads k Setting the Display Format SET UP Display 1 On the Setup screen highlight Display 2 Press the function key for the item you want to set then press...

Page 62: ...orm 1 10 2 0 01 x x 1010 Norm 2 10 9 0 000000001 x x 1010 u To specify the engineering notation display Eng mode Press 4 Eng to switch between engineering notation and standard notation The indicator...

Page 63: ...ution based on number of trials n and probability p random number generation 0 to 1 and storage of result in ListAns random extraction of list data elements and storage of result in ListAns P Q R norm...

Page 64: ...ano 10 9 pico 10 12 femto 10 15 k M G T P E kilo 103 mega 106 giga 109 tera 1012 peta 1015 exa 1018 ENG ENG shifts the decimal place of the displayed value three digits to the left right and decreases...

Page 65: ...is not necessary k Logarithmic and Exponential Functions Be sure to specify Comp for Mode in the Setup screen Example Operation log 1 23 log101 23 0 08990511144 l1 23w log28 3 4 MATH 2 logab 2e8w Lin...

Page 66: ...0 digit random numbers randomly or sequentially from 0 to 1 Ran returns a single random number while RanList returns multiple random numbers in list form The following shows the syntaxes of Ran and Ra...

Page 67: ...s Example Operation RanList 4 Generates four random numbers and displays the result on the ListAns screen K6 g 3 PROB 4 RAND 5 List 4 w RanList 3 1 Generates from the first to the third random numbers...

Page 68: ...andom Number Generation in Accordance with Normal Distribution RanNorm This function generates a 10 digit random number in accordance with normal distribution based on a specified mean and standard de...

Page 69: ...list K6 g 3 PROB 4 RAND 4 Bin 5 0 5 3 w u Random Extraction of List Data Elements RanSamp This function randomly extracts elements from list data and returns the results in list format RanSamp List X...

Page 70: ...Permutation u Combination Be sure to specify Comp for Mode in the Setup screen Example 1 To calculate the possible number of different arrangements using 4 items selected from among 10 items Formula O...

Page 71: ...o determine the least common multiple of 9 and 15 LCM 9 15 45 K6 g 4 NUMERIC 6 g 3 LCM 9 15 w k Division Remainder MOD Remainder of Exponential Division MOD_Exp Example Operation To determine the rema...

Page 72: ...ds 10 the fraction is automatically displayed in decimal format 3 Calculations containing both fractions and decimals are calculated in decimal format Pressing the M key toggles the display fraction b...

Page 73: ...B 1 Operation Display 3aav A w 2aal B w av A K6 g 6 g 4 LOGIC 1 And al B w 1 u About Logical Operations A logical operation always produces either 0 or 1 as its result The following table shows all o...

Page 74: ...n f x function solution FMin FMax logab minimum value maximum value summation logarithm logab k Quotient of Integer Integer OPTN CALC Int The Int function can be used to determine the quotient when on...

Page 75: ...fied divisor n Under initial default settings this calculator automatically simplifies fraction calculation results before displaying them Before performing the following examples use the Setup screen...

Page 76: ...on mode This input method is recommended for most normal Solve function input An error Time Out occurs when there is no convergence of the solution For information about Solve calculations see page 4...

Page 77: ...en there may be solutions other than those displayed by SolveN Example To solve x2 5x 6 0 K4 CALC 5 SolveN vx fv g w J k First Derivative Calculations OPTN CALC d dx To perform first derivative calcul...

Page 78: ...bles A through Z excluding X r are treated as constants and the value currently assigned to that variable is applied during the calculation Pressing A during calculation of a first derivative while th...

Page 79: ...pproximates f a Example To determine the second derivative at x 3 for the function y x3 4x2 x 6 Input the function f x AK4 CALC 3 d2 dx2 vMde evx v ge Input 3 as point a which is the derivative point...

Page 80: ...tion above integration calculations are performed by calculating integral values from a through b for the function y f x where a x b and f x 0 This in effect calculates the surface area of the shaded...

Page 81: ...e part S 2 When minute fluctuations in integration divisions produce large fluctuations in integration values calculate the integration divisions separately divide the large fluctuation areas into sma...

Page 82: ...tput mode the tolerance value is fixed at 1E 5 and cannot be changed k Calculations OPTN CALC To perform calculations first display the function analysis menu and then input the values using the synta...

Page 83: ...tions OPTN CALC FMin FMax After displaying the function analysis menu you can input maximum minimum calculations using the formats below and solve for the maximum and minimum of a function within inte...

Page 84: ...n division parentheses calculations function calculations and memory calculations with complex numbers just as you do with the manual calculations described on pages 2 1 to 2 17 The input output range...

Page 85: ...Solutions obtained by the Real a bi and r modes are different for power root x calculations when x 0 and y m n when n is an odd number Example 3x 8 2 Real 1 1 732050808i a bi 2 60 r Deg mode To input...

Page 86: ...a Gaussian plane and calculates absolute value Z and argument arg Example To calculate absolute value r and argument for the complex number 3 4i with the angle unit set for degrees Imaginary axis Rea...

Page 87: ...m a complex number of the form a bi Example To extract the real and imaginary parts of the complex number 2 5i AK3 COMPLEX 6 g 1 ReP c f6 g 1 i w Real part extraction AK3 COMPLEX 6 g 2 ImP c f6 g 1 i...

Page 88: ...shows the numerals that can be used in each number system Binary 0 1 Octal 0 1 2 3 4 5 6 7 Decimal 0 1 2 3 4 5 6 7 8 9 Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F Negative binary octal and hexadecima...

Page 89: ...adecimal binary octal conversion menu u To specify a number system for an input value You can specify a number system for each individual value you input Press 1 d o to display a menu of number system...

Page 90: ...Operations Example To input and execute 12016 and AD16 m SET UP Move the highlighting to Mode and then press 3 Hex J Abca2 LOGIC 3 and ADw k Number System Transformation Press 3 DISPLAY to display a...

Page 91: ...99 and the maximum number of columns is 999 Important You can input either an upper case X a X or lower case x v for matrix memory Mat X Both Mat X and Mat x refer to the same memory area About Matrix...

Page 92: ...rix in the area named Mat B Highlight Mat B c 3 DIM This step can be omitted Specify the number of rows cw Specify the number of columns dw w All of the cells of a new matrix contain the value 0 Chang...

Page 93: ...While the Matrix Editor is on the display press 2 DEL ALL 2 Press 1 Yes to delete all matrices in memory or 6 No to abort the operation without deleting anything k Matrix Cell Operations Use the follo...

Page 94: ...another row u To swap two rows Example To swap rows two and three of the following matrix All of the operation examples are performed using the following matrix Matrix A 1 2 3 4 5 6 1 ROW OP 1 SWAP I...

Page 95: ...of row whose product should be calculated cw Specify number of row where result should be added dww A complex number also can be input as multiplier value k u To add two rows together Example To add...

Page 96: ...etween rows one and two 2 ROW c 2 INSERT u To add a row Example To add a new row below row 3 2 ROW cc 3 ADD u Column Operations DELETE delete column INSERT insert column ADD add column u To delete a c...

Page 97: ...file you want to import and then press w This imports the contents of the CSV file you specified to the matrix memory Important Attempting to import the following types of CSV files will result in an...

Page 98: ...e Delimiter Symbol and Decimal Point page 3 20 k Modifying Matrices Using Matrix Commands OPTN MAT VCT u To display the matrix commands 1 From the Main Menu enter the Run Matrix mode 2 Press K to disp...

Page 99: ...he maximum value of both m and n is 999 An error occurs if memory becomes full as you are inputting data You can also use the above format inside a program that inputs matrix data u To input an identi...

Page 100: ...or Matrix B c d a K2 MAT VCT 6 g 2 Dim 6 g 1 Mat al B w The Dim command can be used to check and configure vector dimension settings u Modifying Matrices Using Matrix Commands You can also use matrix...

Page 101: ...le matrix Example 1 To fill all of the cells of Matrix A with the value 3 K2 MAT VCT 6 g 3 Fill d 6 g 1 Mat av A w The Fill command can be used to write the same value into all vector elements Example...

Page 102: ...ommand menu to perform matrix calculation operations u To display the matrix commands 1 From the Main Menu enter the Run Matrix mode 2 Press K to display the option menu 3 Press 2 MAT VCT to display t...

Page 103: ...ust match the number of rows in Matrix 2 Otherwise an error occurs u Determinant OPTN MAT VCT Det Example Obtain the determinant for the following matrix Matrix A 1 2 3 4 5 6 1 2 0 K2 MAT VCT 3 Det 1...

Page 104: ...n command can be used with a vector as well It converts a 1 row n column vector to an n row 1 column vector or an m row 1 column vector to a 1 row m column vector u Row Echelon Form OPTN MAT VCT Ref T...

Page 105: ...t av A x 1 w Only square matrices same number of rows and columns can be inverted Trying to invert a matrix that is not square produces an error A matrix with a determinant of zero cannot be inverted...

Page 106: ...power calculations calculation is possible up to a power of 32766 u Determining the Absolute Value Integer Part Fraction Part and Maximum Integer of a Matrix OPTN NUMERIC Abs Frac Int Intg Example To...

Page 107: ...ue to dropped digits Matrix operations are performed individually on each cell so calculations may require considerable time to complete The calculation precision of displayed results for matrix calcu...

Page 108: ...ons Determination of the vector norm size Determination of the angle formed by two vectors Determination of the unit vector Important You can input either an upper case X a X or lower case x v for vec...

Page 109: ...g the dimension always limited to m rows 1 column or 1 row n columns k Vector Calculations OPTN MAT VCT Use the vector command menu to perform vector calculations u To display vector commands 1 From t...

Page 110: ...ctor memory contents can be assigned to matrix memory if you want Vct Mat In the above and are any variable names A through Z u Vector Data Input Format OPTN MAT VCT Vct The following shows the format...

Page 111: ...1 Vct av A 1 Vct al B w Example 3 To determine the product of the matrix and vector shown below Mat A Vct B Mat A Vct B K2 MAT VCT 1 Mat av A 6 g 6 g 1 Vct al B w When performing addition or subtract...

Page 112: ...the angle formed by two vectors Vct A 1 2 Vct B 3 4 K2 MAT VCT 6 g 6 g 4 Angle 1 Vct av A 1 Vct al B w u Unit Vector OPTN MAT VCT UnitV Example Determine the unit vector of the vector below Vct A 5 5...

Page 113: ...lication is installed Display Name Category Display Name Category Display Name Category LENGTH Length TMPR Temperature PRESSURE Pressure AREA Area VELOCITY Velocity ENERGY Energy Work VOLUME Volume MA...

Page 114: ...al numbers or a list that contains real number elements only can be used as the value being converted from When values being converted from are input into a list or when list memory is specified conve...

Page 115: ...fluid ounce U S l y light year gal US gallon pc parsec gal UK UK gallon Mil 1 1000 inch pt pint in inch qt quart ft foot tsp teaspoon yd yard tbsp tablespoon fath fathom cup cup rd rod Time ns nanose...

Page 116: ...er mg milligram Energy Work eV electron Volt g gram J Joule kg kilogram calth calorieth mton metric ton cal15 calorie 15 C oz avoirdupois ounce calIT calorieIT lb pound mass kcalth kilocalorieth slug...

Page 117: ...name sub name or cell you want to select Note that c does not move the highlighting to a cell that does not contain a value The screen automatically scrolls when the highlighting is located at either...

Page 118: ...each one Press after inputting the final value g h i 3 Press w to store all of the values in your list w Remember that a comma separates values so you should not input a comma after the final value of...

Page 119: ...to move the highlighting to the cell you want to delete 2 Press 6 g 3 DELETE to delete the selected cell and cause everything below it to be shifted up The cell delete operation does not affect cells...

Page 120: ...you insert a cell is somehow related to the data in neighboring lists inserting a cell can cause related values to become misaligned k Naming a List You can assign List 1 through List 26 sub names of...

Page 121: ...idual cell or for all of the data input in a particular list u To change the data color in a specific cell 1 Use the cursor keys to move the highlighting to the cell whose character color you want to...

Page 122: ...any data input into any cell that did not previously contain data will be the default color black Note that this operation does not change the color of the sub name k Sorting List Values You can sort...

Page 123: ...ascending order Here we will specify List 1 bw 4 In response to the Select Second List List No prompt input the number of the list you want to link to the base list Here we will specify List 2 cw Desc...

Page 124: ...Lst Mat 1 List list number 1 26 1 List list number 1 26 1 List list number 1 26 w You can skip input 1 List in the part of the above operation All the lists must contain the same number of data items...

Page 125: ...value 1 List list number 1 26 w Example To replace all data items in List 1 with the number 3 AK1 LIST 4 Fill d 1 List b w The following shows the new contents of List 1 u To generate a sequence of nu...

Page 126: ...the greatest value K1 LIST 6 g 2 Max 6 g 6 g 1 List b 1 List c w u To calculate the mean of data items OPTN LIST Mean K1 LIST 6 g 3 Mean 6 g 6 g 1 List list number 1 26 w Example To calculate the mea...

Page 127: ...t number 1 26 1 List list number 1 26 w Example To combine the List 1 3 2 and List 2 1 9 10 AK1 LIST 6 g 5 Augment 6 g 6 g 1 List b 1 List c w u To calculate the sum of data items in a list OPTN LIST...

Page 128: ...4 6 g 1 List list number 1 26 w The above operation calculates what percentage of the list total is represented by each data item The result of this operation is stored in ListAns Memory Example To c...

Page 129: ...ells in the original list An error occurs if you execute List for a list that has no data or only one data item 3 Arithmetic Calculations Using Lists You can perform arithmetic calculations using two...

Page 130: ...the Run Matrix mode perform the following key operation AK1 LIST 1 List Enter the List command 2 Enter the list number integer from 1 to 26 you want to specify u To specify the sub name of a list cre...

Page 131: ...t cell You can input a value into a specific list cell inside a list When you do the value that was previously stored in the cell is replaced with the new value you input Example To input the value 25...

Page 132: ...the Table mode to input values that result from certain scientific function calculations into a list To do this first generate a table and then use the list copy function to copy the values from the...

Page 133: ...tween List Files You can store up to 26 lists List 1 to List 26 in each file File 1 to File 6 A simple operation lets you switch between list files u To switch between list files 1 From the Main Menu...

Page 134: ...r the line break code When importing a CSV file to the calculator if the data in Line 1 of each column of the file or Line 1 of Column 1 of the file contains double quotation marks or a single quotati...

Page 135: ...t 1 List 2 List 3 List 4 List 5 Highlighting 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 Import CSV File Data 20 20 20 30 30 30 40 40 40 List Editor Content following Import List 1 List 2 List 3 List 4 Li...

Page 136: ...ne format Example 2 3 4 2 3 4 and data Converted to a decimal value Example 3 1 732050808 k Specifying the CSV File Delimiter Symbol and Decimal Point When importing a CSV file that has been transferr...

Page 137: ...unknowns 3 Sequentially input the coefficients The cell that is currently selected for input is highlighted Each time you input a coefficient the highlighting shifts in the sequence a1 b1 c1 an bn cn...

Page 138: ...lution x y z of a simultaneous linear equation with three unknowns Because of this precision is reduced as the value of the determinant approaches zero Also simultaneous equations with three or more u...

Page 139: ...sequence a b c You can also input fractions and values assigned to variables as coefficients You can cancel the value you are inputting for the current coefficient by pressing J at any time before you...

Page 140: ...the equation has multiple solutions After calculation is complete you can press 1 REPEAT change coefficient values and then re calculate 3 Solve Calculations The Solve calculation mode lets you determ...

Page 141: ...re the real solution The closer the difference between the Lft and Rgt values is to zero the lower degree of error in the result Example An object thrown into the air at initial velocity V takes time...

Page 142: ...pages 5 48 and 5 49 1 Sample Graphs k Graph Relation List Screen and Graph Color A graph relation list screen table relation list screen like the one shown below appears first whenever you enter the...

Page 143: ...How to draw a simple graph 1 To draw a graph simply input the applicable function 1 From the Main Menu enter the Graph mode 2 Input the function you want to graph Here you would use the V Window to s...

Page 144: ...tion type 6 g 1 Y to 4 Y Y inequality on left side 6 g 6 g 1 X to 4 X X inequality on left side Repeat this step as many times as required to input all of the functions you want Next you should specif...

Page 145: ...you can use to change the graph line style and graph line color For details see Changing Graph Properties page 5 15 Example 1 Input the functions shown below and draw their graphs Y1 2x2 3 r2 3sin2 1...

Page 146: ...r T min T max Minimum maximum T values T ptch T pitch 3 Press c to move the highlighting and input an appropriate value for each parameter pressing w after each INITIAL TRIG STANDRD V Window initial s...

Page 147: ...aph will appear coarse if the settings you make in the V Window cause the T ptch value to be too large relative to the differential between the T min and T max settings If the settings you make cause...

Page 148: ...e a range start point end point for a function before graphing it 1 From the Main Menu enter the Graph mode 2 Configure V Window settings 3 Specify the function type and input the function The followi...

Page 149: ...its original size following a zoom operation 6 g 2 SQUARE Graph correction V Window x axis values are corrected so they are identical to the y axis values 6 g 3 ROUND Coordinate rounding Rounds the co...

Page 150: ...Zoom In Zoom Out Using Key Operations You can use the and keys while the graph screen is on the display to zoom in and out on the center of the graph screen The zoom operations are performed in accor...

Page 151: ...played as the graph background image Use the Background setting on the Setup screen to specify the background image The following describes the types of files that can be used as the background image...

Page 152: ...exit the V Window screen press J u To update the background image V Window settings with current V Window settings 1 While the graph screen is on the display press K4 BGV WIN 2 Press 1 SAVE This will...

Page 153: ...ground You can use this setting to adjust the background image to a level that makes the graph easier to see Note that the lightness setting can be adjusted only when the background image is a 16 bit...

Page 154: ...f y X f y X f y inequality graph CONVERT Y Y Y Y Y X X X X X changes the function type of the selected expression 2 Press the function key that corresponds to the graph type you want to specify k Sto...

Page 155: ...expression dcvw Inputs and stores y expression u To create a composite function Example To use relations in Y1 and Y2 to create composite functions for Y3 and Y4 Y1 x 1 Y2 x2 3 Assign Y1 Y2 to Y3 and...

Page 156: ...1 Y b av A a w J4 GRAPH 1 Y b av A b w ffff1 SELECT 6 DRAW The above screens are produced using the Trace function See Function Analysis page 5 52 for more information k Changing Graph Properties u T...

Page 157: ...e setting is the way you want press J u To change graph properties from the graph screen 1 While the graph screen is on the display press f FORMAT If there are multiple graphs on the graph screen one...

Page 158: ...xpression in memory area Y1 from y 2x2 5 to y 2x2 3 e Displays cursor eeeeeDd Changes contents w Stores new graph function u To change the type of a function 1 1 While the graph relation list is on th...

Page 159: ...2 Press 1 SELECT Each press of 1 SELECT toggles graphing on and off 3 Press 6 DRAW Example To select the following functions for drawing Y1 2x2 5 r2 5 sin3 Use the following V Window settings Xmin 5 X...

Page 160: ...uses scale lines to be displayed for the x axis and y axis Label On Axes On Grid Off This setting display x axis y axis and origin O labels Even if the Grid setting is On or Line grid lines will not b...

Page 161: ...hen press w Pressing bw recalls the graph function in Graph Memory 1 G Mem1 Recalling data from graph memory causes any data currently on the graph relation list to be deleted 4 Saving and Recalling G...

Page 162: ...of graph that uses a split screen cannot be saved in picture memory u To save a graph screen image to Picture Memory 1 While the graph screen is on the display press K1 PICTURE 1 STORE 1 1 20 2 On th...

Page 163: ...mediately behind the graph above the current background image on the graph screen To clear a recalled image display the graph screen and then press 4 SKETCH 1 Cls u To recall an image stored in Pictur...

Page 164: ...ph to the sub screen 1 From the Main Menu enter the Graph mode 2 On the Setup screen select G G for Dual Screen 3 Configure V Window settings for the main screen Press 6 RIGHT to display the sub graph...

Page 165: ...he graph the changes will be applied to both graphs You cannot change the graph properties of an expression marked with R on the graph relation list screen For details about how to change graph proper...

Page 166: ...1 m Run Matrix 2 m SET UP 2 Line J 3 3 V WIN fwfwcwc bawbawfwJ 4 4 SKETCH 1 Cls w 5 GRAPH 1 Y 5 cvx dv ew Certain functions can be graphed easily using built in function graphs You can draw graphs of...

Page 167: ...anges in the sequence 3 1 1 Use the following V Window settings Xmin 5 Xmax 5 Xscale 1 Ymin 10 Ymax 10 Yscale 2 1 m Graph 2 m SET UP cccc3 Off J 3 3 V WIN fwfwbwc bawbawcwJ 4 3 TYPE 1 Y av A vx d av A...

Page 168: ...ation list screen Example List 1 1 2 3 List 2 4 5 6 Registering and graphing the expression Y1 List 1 X2 will simultaneously draw graphs for the following three expressions Y X2 Y 2X2 Y 3X2 Registerin...

Page 169: ...yellow is specified for the expression the default color for the graph relation list screen line where the expression is registered will be used instead You cannot change the line color or line style...

Page 170: ...wn as the result of a paste operation is drawn with blue line color and normal line style You can change the line color and line style on the graph screen only For details see Changing Graph Propertie...

Page 171: ...ric table Table range method With this method you specify the conditions for the change in value of the variable List With this method the data in the list you specify is substituted for the x variabl...

Page 172: ...changing the graph line color from the graph relation list screen For details see To change graph properties from the graph relation list screen page 5 15 u Generating a Table Example To generate a ta...

Page 173: ...ponds to the function type you want to specify The number table is generated only for the function type specified on the relation list Table Func You cannot generate a number table for a mixture of di...

Page 174: ...d then press w bw The color of the text in the list where you perform the paste operation will be black k Drawing a Graph from a Number Table Use the following procedure to generate a number table and...

Page 175: ...the properties of a graph after you draw using a number table For details see To change graph properties from the graph screen page 5 16 k Simultaneously Displaying a Number Table and Graph Specifying...

Page 176: ...e the following V Window settings Xmin 0 Xmax 6 Xscale 1 Ymin 2 Ymax 10 Yscale 2 1 m Table 2 3 V WIN awgwbwc cwbawcwJ 3 m SET UP ccc1 T G J 4 3 TYPE 1 Y dvx cw 5 5 SET dwdwbwJ 6 6 TABLE 7 5 GPH CON Th...

Page 177: ...isplayed in the lower left corner of the screen while the Modify function is running The variable or step value that you can modify is displayed in magenta Use d and e to modify the value of the magen...

Page 178: ...raw the graph function you entered in step 4 6 Use f and c to select Step which will change its color to magenta and then use the number keys to enter a step value 7 Use f and c to select the variable...

Page 179: ...bserve the changes in the graph 1 From the Main Menu enter the Conic Graphs mode 2 Press 3 PARAM to display the parametric equation list 3 Use c to move the highlighting to X H T Y K AT2 and then pres...

Page 180: ...reen 2 Use f and c to move the highlighting to the area to which you want to copy the graph expression 3 Press w This copies the expression and returns to the graph screen You can view the copied expr...

Page 181: ...and increment 8 Specify the drawing speed 3 SPEED 1 Pause after each draw Stop Go 3 2 Half normal speed Slow 3 Normal speed Normal 4 Twice normal speed Fast 9 Draw the Dynamic Graph 1 The following ar...

Page 182: ...raph Locus Turning on the Dynamic Graph locus setting on the Setup screen lets you overlay a graph drawn by changing the coefficient values 1 From the Main Menu enter the Dyna Graph mode 2 Configure V...

Page 183: ...or every other dot This setting is value for Dynamic Func Y graphic only 1 Press m SET UP to display the Setup screen 2 Press ccc to select Y Draw Speed 3 Select the graphing method 1 Norm Draws all...

Page 184: ...la You can input up to three of the following types of recursion formulas and generate a number table General term of sequence an composed of an n Linear two term recursion composed of an 1 an n Linea...

Page 185: ...ormula you can graph the values on a line graph or plot type graph 1 From the Main Menu enter the Recursion mode 2 Configure V Window settings 3 Specify the recursion formula type and input the formul...

Page 186: ...nput in the Recursion mode with one value on the horizontal axis and the other value on the vertical axis For an an 1 an 2 bn bn 1 bn 2 cn cn 1 cn 2 the numeric sequence of the alphabetically first ex...

Page 187: ...you want to use to draw the phase plot To do so use the function menu that appears when you press 3 PHASE on the table screen 1 a b Graph using an an 1 an 2 and bn bn 1 bn 2 2 b c Graph using bn bn 1...

Page 188: ...r sequences an an 1 an 2 and cn cn 1 cn 2 k WEB Graph Convergence Divergence y f x is graphed by presuming an 1 y an x for linear two term recursion an 1 f an composed of an 1 an Next it can be determ...

Page 189: ...ange the graph line style press 1 SEL S after step 4 With WEB Graph you can specify the line type for a y f x graph The line type setting is valid only when Connect is selected for Draw Type on the Se...

Page 190: ...a circle graph 1 m Conic Graphs 2 1 RECT c X AY2 BY C w 3 cwbw bw6 DRAW 4 JJ 5 2 POL cccc R 2Acos w 6 cw6 DRAW In the Conic Graphs mode you can press 1 MODIFY in place of 6 DRAW while the coefficient...

Page 191: ...w the graph 6 Select the sketch function you want to use 1 4 SKETCH 1 Cls Screen clear 2 Tangent Tangent line 3 Norm Line normal to a curve 4 Inverse Inverse function 2 6 g 1 PLOT Plot PlotOn PlotOff...

Page 192: ...ol settings are always applied for an inverse function graph 3 Some sketch functions require specification of two points After you press w to specify the first point use the cursor keys to move the po...

Page 193: ...of the pointer Also supplementary lines appear from the pointer to the x axis and y axis You can hide the supplementary lines by pressing c To redisplay hidden lines press f 5 You can also move the po...

Page 194: ...3 Draw the graph 4 Press 1 TRACE and the pointer appears at the center of the graph The current coordinates and the derivative also appear on the display at this time k Graph to Table You can use tra...

Page 195: ...oot of the graph 2 MAX Maximum value of the graph 3 MIN Minimum value of the graph 4 Y ICEPT y intercept of the graph 5 INTSECT Intersection of two graphs 6 g 1 Y CAL y coordinate for a given x coordi...

Page 196: ...g on the Setup screen the derivative will be displayed along with the root when you calculate the root of a graph using the above procedure u To calculate the point of intersection of two graphs 1 Dra...

Page 197: ...to perform 5 G SOLVE 6 g 1 Y CAL y coordinate for given x 6 g 2 X CAL x coordinate for given y 3 If there are multiple graphs on the graph screen one of them will start flashing Use f and c to move th...

Page 198: ...at 2 0 Y1 x x 2 x 2 You can also specify the lower limit and upper limit by inputting them on the 10 key pad When setting the range make sure that the lower limit is less than the upper limit Integra...

Page 199: ...ction point on the display the message Not Found will appear In this case press J 3 Use d and e to move the pointer to the intersection point you want to use as the lowermost side of the integration r...

Page 200: ...egration region and then press w 5 Press w to calculate the integrated value and the area value Example To graph Y1 X3 7X2 2X 15 and Y2 5X 20 specify the intersect of the graph and the root of graph Y...

Page 201: ...h Analysis FOCUS VERTEX CENTER e focus vertex center eccentricity X ICEPT Y ICEPT x intercept y intercept u Hyperbolic Graph Analysis FOCUS VERTEX CENTER e focus vertex center eccentricity ASYMPT asym...

Page 202: ...e to calculate the second vertex Pressing d returns to the first vertex Pressing e when calculating the vertices of an ellipse will calculate the next value Pressing d will scroll back through previou...

Page 203: ...c d and e to move the highlighting around the lists Once you input data you can use it to produce a graph and check for tendencies You can also use a variety of different regression calculations to an...

Page 204: ...ate lists This setting specifies the list List 1 List 2 etc to be used for the frequency column when drawing a statistical graph The initial default setting for this item is 1 which indicates that the...

Page 205: ...regression graph logistic regression graph XList x axis data list YList y axis data list LIST List 1 to 26 Frequency number of times a value occurs 1 1 to 1 plot LIST List 1 to 26 Mark Type plot mark...

Page 206: ...Frequency data list are the different colors plot marks and lines are represented as described below Hist Graph is shaded with the applicable color Broken Graph plot marks are shown as and lines are...

Page 207: ...or each data element display as percentage display as value Sto Mem Specifies storage of percentage values to a list None List For percentage values Do not store to list Specify List 1 to 26 and store...

Page 208: ...e Red Magenta Green Cyan Yellow Specifies a single color for the border line Whisker Specifies the whisker color from the box ends to minX and maxX Settings are the same as those for Box Outlier Color...

Page 209: ...3 2 Use the cursor keys to move the highlighting to the graph whose status you want to change and press the applicable function key to change the status On Off On draw Off non draw DRAW draws all On...

Page 210: ...ph k Normal Probability Plot This plot compares the data accumulated ratio with a normal distribution accumulated ratio XList specifies the list where data is input and Mark Type is used to select fro...

Page 211: ...c ranges A box encloses all the data in an area from the first quartile Q1 to the third quartile Q3 with a line drawn at the median Med Lines called whiskers extend from either end of the box up to th...

Page 212: ...with two or three lists specified and the specified lists have a different number of list elements A Condition ERROR occurs when lists are assigned for Data1 and Data3 while None is specified for Dat...

Page 213: ...scribes the meaning of each of the parameters x mean x sum x2 sum of squares x population standard deviation sx sample standard deviation n number of data items minX minimum Q1 first quartile Med medi...

Page 214: ...n items from the bottom of the population Q3 median of the group of 2 n items from the top of the population Med 2 n th and 2 n 1 th element average value Center Point Center Point Center Point When...

Page 215: ...ive frequency ratio is greater than 0 5 and nearest to 0 5 When the cumulative frequency ratio for some data value is exactly 0 5 Med is the average of that data value and the next data value The foll...

Page 216: ...7 5 1 8 8 10 0 8 6 1 9 9 10 0 9 7 1 10 10 10 1 0 3 is the value of whose cumulative frequency ratio is greater than or equal to 0 25 and nearest to 0 25 so Q1 3 5 is the value of whose cumulative freq...

Page 217: ...atter diagram or xyLine xy line graph as the graph type and then execute the graph operation Press A J or J QUIT to return to the List Editor Example Input the two sets of data shown below Next plot t...

Page 218: ...2 2 4 4 0 5 2 xList 2 1 0 3 1 5 2 0 2 4 yList 1 m Statistics 2 a fwb cwc ewewf cwe c bwa dwb fwcwc ew 1 GRAPH 6 SET c1 Scatter J1 GRAPH1 3 1 CALC 6 g 2 Log 4 6 DRAW You can perform trace on a regressi...

Page 219: ...except for Med Med sinusoidal regression and logistic regression MSe mean square error except for Med Med k Graphing Statistical Calculation Results While the parameter calculation result is on the d...

Page 220: ...ffects of extreme values 1 CALC 3 Med 6 DRAW The following is the Med Med graph model formula y ax b a Med Med graph slope b Med Med graph y intercept k Quadratic Cubic Quartic Regression Graph A quad...

Page 221: ...regression coefficient k Exponential Regression Graph Exponential regression expresses y as a proportion of the exponential function of x The standard exponential regression formula is y a ebx so if...

Page 222: ...ssion model formula y a xb a regression coefficient b regression power k Sinusoidal Regression Graph Sinusoidal regression is best applied for cyclical data The following is the sinusoidal regression...

Page 223: ...ated during regression calculations While the List Editor is on the display recall the Setup screen to specify a LIST List 1 through List 26 for Resid List Calculated residual data is stored in the sp...

Page 224: ...ion of data stored in yList sy sample standard deviation of data stored in yList xy sum of the product of data stored in xList and yList minX minimum of data stored in xList maxX maximum of data store...

Page 225: ...values XList 2Var YList location of paired variable statistic y values YList 2Var Freq location of paired variable frequency values Frequency Calculations in this section are performed based on the ab...

Page 226: ...Logistic Regression Graph regression calculation results were displayed after the graph was drawn Here each coefficient value of the regression line or regression curve is expressed as a number You c...

Page 227: ...are error MSe Displayed following any regression calculation except Med Med Depending on the regression calculation type mean square error MSe is obtained using the following formulas Linear Regressio...

Page 228: ...the value you want for x and then press w This causes the coordinates for x and y to appear at the bottom of the display and moves the pointer to the corresponding point on the graph The pointer does...

Page 229: ...n use the Run Matrix mode to calculate estimated values for the regression graph s x and y Example To perform a linear regression using the nearby data and estimate the values of and x when xi 20 and...

Page 230: ...and R t and normalized variate t x are calculated using the following formulas Standard Normal Distribution Example The following table shows the results of measurements of the height of 20 college st...

Page 231: ...l calculations only 2 CALC 6 SET 1 LIST bw c2 LIST cw J QUIT 2 CALC 1 1 VAR 4 Press m select the Run Matrix mode press K6 g 3 PROB 6 g to recall the probability calculation PROB menu 3 PROB 6 g 4 t bg...

Page 232: ...the Distribution Function You can use special functions in the Run Matrix mode or Program mode to perform calculations that are the same as the Statistics mode distribution function calculation page...

Page 233: ...ntax StdDev List n List m StdDev_ List n List m Variance List n List m Variance_ 2 List n List m List n Sample data List m Frequency data Example To store the x data below in List 1 the frequency valu...

Page 234: ...standard deviation 1 sample mean o 1 number of samples n 2 condition 0 can be specified by entering 0 as the initial argument of the one sample Z test command OneSampleZTest 1 From the Main Menu ente...

Page 235: ...an when the population standard deviation is unknown 2 Sample t Test compares the population means when the population standard deviations are unknown LinearReg t Test calculates the strength of the l...

Page 236: ...ple F Test or Two Way ANOVA screen To display the 1 Sample Z Test input screen for example display the List Editor and then press 3 TEST 1 Z 1 1 SAMPLE 2 Move the highlighting to GphColor and then pre...

Page 237: ...meter data specification items that are different from list data specification Calculation Result Output Example 11 4 direction of test sx Displayed only for Data List setting Save Res does not save t...

Page 238: ...Displayed only for Data List setting Save Res does not save the 1 condition in line 2 u 1 Prop Z Test This test is used to test for an unknown proportion of successes The 1 Prop Z Test is applied to t...

Page 239: ...g graph analysis functions after drawing a t Test result output graph 1 T Displays t score Pressing 1 T displays the t score at the bottom of the display and displays the pointer at the corresponding...

Page 240: ...1 SAMPLE The following shows the parameter data specification items that are different from list data specification Calculation Result Output Example 11 3 direction of test Save Res does not save the...

Page 241: ...earReg t Test LinearReg t Test treats paired variable data sets as x y pairs and uses the method of least squares to determine the most appropriate a b coefficients of the data for the regression form...

Page 242: ...e the following graph analysis functions after drawing a graph 1 CHI Displays 2 value Pressing 1 CHI displays the 2 value at the bottom of the display and displays the pointer at the corresponding loc...

Page 243: ...output of contribution values 2 two way Test 2 two way Test sets up a number of independent groups and tests hypothesis related to the proportion of the sample included in each group The 2 Test is app...

Page 244: ...a calculation result is displayed enters the Matrix Editor which you can use to edit and view the contents of matrices Switching from the Matrix Editor to the Vector Editor is not supported k 2 Sampl...

Page 245: ...y ANOVA is used when there are two independent variables and one dependent variable Perform the following key operations from the List Editor 3 TEST 5 ANOVA The following is the meaning of each item i...

Page 246: ...Way ANOVA Two Way ANOVA Data List1 1 1 2 2 List2 124 913 120 1001 List1 1 1 1 1 2 2 2 2 List2 1 1 2 2 1 1 2 2 List3 113 116 139 132 133 131 126 122 Setup Screen Calculation Result One Way ANOVA Line 1...

Page 247: ...y stores the number of conditions to variable A and the mean value to variable M respectively k ANOVA Two Way u Description The nearby table shows measurement results for a metal product produced by a...

Page 248: ...so the hypothesis is not rejected Temperature differential B level of significance P 0 04222398836 The level of significance p 0 04222398836 is less than the significance level 0 05 so the hypothesis...

Page 249: ...alculates the confidence interval for an unknown population mean when the population standard deviation is known 2 Sample Z Interval calculates the confidence interval for the difference between two p...

Page 250: ...ation mean when the population standard deviation is known Perform the following key operations from the List Editor 4 INTR 1 Z 1 1 SAMPLE The following shows the parameter data specification items th...

Page 251: ...2 Prop Z Interval 2 Prop Z Interval uses the number of data items to calculate the confidence interval for the difference between the proportion of successes in two populations Perform the following k...

Page 252: ...l distribution centered on the greatest occurrences of mean data highest frequency with the frequency decreasing as you move away from the center Poisson distribution geometric distribution and variou...

Page 253: ...de screen press 5 DIST to display the distribution menu which contains the following items 5 DIST 1 NORM Normal distribution page 6 52 2 t Student t distribution page 6 54 3 CHI 2 distribution page 6...

Page 254: ...r to the corresponding point on the graph 3 Pressing v or a number key at this time causes the x value input dialog box to reappear so you can perform another estimated value calculation if you want 4...

Page 255: ...stribution between a lower bound and an upper bound Calculation Result Output Examples When a list is specified Graph when an x value is specified Graphing is supported only when a variable is specifi...

Page 256: ...ecified Graph when variable x is specified Graphing is supported only when a variable is specified and a single x value is entered as data Student t Cumulative Distribution 5 DIST 2 t 2 tcd Student t...

Page 257: ...There is no graphing for Inverse Student t Cumulative Distribution k 2 Distribution 2 Probability Density 5 DIST 3 CHI 1 Cpd 2 Probability Density calculates the 2 probability density p for a specifie...

Page 258: ...pecified Graphing is supported only when a variable is specified and a single x value is entered as data Inverse 2 Cumulative Distribution 5 DIST 3 CHI 3 InvC Inverse 2 Cumulative Distribution calcula...

Page 259: ...is specified Graph when variable x is specified Graphing is supported only when a variable is specified and a single x value is entered as data F Cumulative Distribution 5 DIST 4 F 2 Fcd F Cumulative...

Page 260: ...aphing for Inverse F Cumulative Distribution k Binomial Distribution Binomial Probability 5 DIST 5 BINOMIAL 1 Bpd Binomial Probability calculates a probability at a specific single x value or each lis...

Page 261: ...tput Examples When a list is specified When variable x is specified There is no graphing for Binomial Cumulative Distribution Inverse Binomial Cumulative Distribution 5 DIST 5 BINOMIAL 3 InvB Inverse...

Page 262: ...message shown below will appear with both values The calculation results of Inverse Binomial Cumulative Distribution are integers Accuracy may be reduced when the Area value has 10 or more digits Not...

Page 263: ...Examples When a list is specified When variable x is specified There is no graphing for Poisson Cumulative Distribution Inverse Poisson Cumulative Distribution 5 DIST 6 g 1 POISSON 3 InvP Inverse Pois...

Page 264: ...alues The calculation results of Inverse Poisson Cumulative Distribution are integers Accuracy may be reduced when the Area value has 10 or more digits Note that even a slight difference in calculatio...

Page 265: ...amples When a list is specified When variable x is specified There is no graphing for Geometric Cumulative Distribution Inverse Geometric Cumulative Distribution 5 DIST 6 g 2 GEO 3 InvG Inverse Geomet...

Page 266: ...ote that even a slight difference in calculation accuracy affects calculation results If a warning message appears check the displayed values k Hypergeometric Distribution Hypergeometric Probability 5...

Page 267: ...pergeometric Cumulative Distribution calculation the calculator uses the specified Area value and the value that is one less than the Area value minimum number of significant digits Area value to calc...

Page 268: ...ample 1 is greater than sample 2 1 Sample t Test population mean value test conditions 0 specifies two tail test 0 specifies lower one tail test 0 specifies upper one tail test 1 2 Sample t Test sampl...

Page 269: ...andard deviation sx 0 sx1 standard deviation of sample 1 sx1 0 sx2 standard deviation of sample 2 sx2 0 XList list for x axis data List 1 to 26 YList list for y axis data List 1 to 26 C Level confiden...

Page 270: ...mean of sample 2 sx sample standard deviation sx1 standard deviation of sample 1 sx2 standard deviation of sample 2 sp pooled sample standard deviation n size of sample n1 size of sample 1 n2 size of...

Page 271: ...n2 1 LinearReg t Test t r n 2 1 r2 b xi o yi p xi o 2 a p bo i 1 n i 1 n 2 GOF Test Oi The i th element of the observed list Ei The i th element of the expected list 2 two way Test Oij The element at...

Page 272: ...1 x2 n2 Z 2 x1 n1 1 x1 n1 n1 x2 n2 1 x2 n2 n2 1 Sample t Interval Lower Upper o tn 1 2 sx n 2 Sample t Interval pooled Lower Upper o1 o2 tn1 n2 2 2 sp 2 1 n1 1 n2 sp n1 1 sx1 2 n2 1 sx2 2 n1 n2 2 2 Sa...

Page 273: ...2 2 df 2 df 1 df x2 1 2 Distribution p x x 0 1 2 df df 2 x 2 1 df 2 1 x 2 e F Distribution ndf 2 x ddf ndf ndf 2 1 ddf ndf x 1 ndf ddf 2 p x 2 ndf ddf 2 ndf 2 ddf x 0 Distribution Inverse Cumulative D...

Page 274: ...Cx N MCn x NCn n Number of elements extracted from population 0 x integer M Number of elements contained in attribute A 0 M integer N Number of population elements n N M N integer Distribution Cumulat...

Page 275: ...r a negative value for the present value PV or the purchase price PRC depends on the type of calculation you are trying to perform 1 Before Performing Financial Calculations From the Main Menu enter t...

Page 276: ...ears to change the graph color The color specification you make on this dialog box is also reflected by the Graph Color setting of the Setup screen Zoom Scroll and Sketch cannot be used in the Financi...

Page 277: ...LE n number of interest periods days I annual interest rate PV principal After configuring the parameters use one of the function menus noted below to perform the corresponding calculation SI simple i...

Page 278: ...es in the reverse direction Press J to return to the parameter input screen 3 Compound Interest This calculator uses the following standard formulas to calculate compound interest u PV PMT FV n I 0 PM...

Page 279: ...2 COMPND from the Financial 1 screen to display the following input screen for compound interest 2 COMPND n number of compound periods I annual interest rate PV present value loan amount in case of l...

Page 280: ...nfiguring the parameters use one of the function menus noted below to perform the corresponding calculation n number of compound periods I annual interest rate PV present value Loan loan amount Saving...

Page 281: ...appraisal can be used to clearly determine whether an investment is realizing profits that were originally targeted u NPV n natural number up to 254 u NFV u IRR In this formula NPV 0 and the value of...

Page 282: ...ation NPV net present value IRR internal rate of return PBP payback period NFV net future value LIST inputs data into a list LIST specifies a list An error occurs if parameters are not configured corr...

Page 283: ...t PM2 PRN e total interest from installment PM1 to payment of installment PM2 INT a b one repayment PMT c a 1 payment Number of Payments 1 PM1 PM2 Last b c a 1 payment Number of Payments 1 PM1 PM2 Las...

Page 284: ...eriods The following calculation is performed after conversion from the nominal interest rate to the effective interest rate and the result is used for all subsequent calculations Press 4 AMORTZN from...

Page 285: ...llment PM1 to installment PM2 COMPND compound interest screen An error occurs if parameters are not configured correctly Use the following function menus to maneuver between calculation result screens...

Page 286: ...VERT n number of compoundings I interest rate After configuring the parameters use one of the function menus noted below to perform the corresponding calculation EFF converts annual percent rate to ef...

Page 287: ...el selling price Mrg margin After configuring the parameters use one of the function menus noted below to perform the corresponding calculation COST cost SELL selling price MARGIN margin An error occu...

Page 288: ...function menus noted below to perform the corresponding calculation PRD number of days from d1 to d2 d2 d1 d1 D d1 plus a number of days d1 D d1 D d1 minus a number of days d1 D An error occurs if par...

Page 289: ...the years digits SYD or declining balance DB Any one of the above methods can be used to calculate depreciation for a specified period A table and graph of the depreciated amount and undepreciated am...

Page 290: ...riginal cost basis FV residual book value j year for calculation of depreciation cost Y 1 number of months in the first year of depreciation n n 1 Z 2 2 n integer part 1 n integer part 2 n fraction pa...

Page 291: ...culated using the declining balance method Calculation Result Output Examples SYD SYD TABLE SYD GRAPH An error occurs if parameters are not configured correctly Use the following function menu to mane...

Page 292: ...date D A INT accrued interest CST price including interest For one or fewer coupon period to redemption For more than one coupon period to redemption u Annual Yield YLD YLD is calculated using Newton...

Page 293: ...ulate the yield to maturity Calculation Result Output Examples PRC PRC GRAPH PRC MEMO An error occurs if parameters are not configured correctly Use the following function menu to maneuver between cal...

Page 294: ...id for a 2 year 730 day 300 loan at a simple annual interest rate of 5 Use a Date Mode setting of 365 1 From the Main Menu enter the Run Matrix mode 2 Press the keys as follows K6 g 6 g 2 FINANCE 1 SI...

Page 295: ...lues to the right of the program list indicate the number of bytes used by each program A file name can be up to eight characters long The following are the characters you can use in a file name A thr...

Page 296: ...the final result of a program executed using this method is on the display re executes the program An error occurs if the program specified by Prog file name cannot be found 2 Program Mode Function K...

Page 297: ...program control command menu JUMP jump command menu input output command CLEAR DISPLAY clear display command menu RELATNL conditional jump relational operator menu I O I O control transfer command men...

Page 298: ...ands in a Program page 8 28 3 Editing Program Contents k Debugging a Program A problem in a program that keeps the program from running correctly is called a bug and the process of eliminating such pr...

Page 299: ...side a Program Example To search for the letter A inside the program named OCTA 1 Recall the program 2 Press 3 SEARCH and input the data you want to find 3 SEARCH av A 3 Press w to begin the search Th...

Page 300: ...ng characters to search for press A to clear your input and re input from the beginning 4 File Management k Deleting a Program u To delete a specific program 1 While the program list is on the display...

Page 301: ...y use f and c to move the highlighting to the file whose name you want to edit and then press 6 g 2 RENAME 2 Make any changes you want 3 Press w to register the new name and return to the program list...

Page 302: ...d in the converted program Converting a program to a text file causes all CASIO scientific function calculator specific commands in the program to be replaced by special corresponding character string...

Page 303: ...is basically the same as the original file except for certain special characters For details about special character exceptions see Program and Text File Conversion Rules page 8 8 If there is already...

Page 304: ...he program file 4 After inputting the program press J QUIT to exit the program file and return to the program list Files that are password protected are indicated by an asterisk to the right of the fi...

Page 305: ...8 20 DrawGraph 8 21 DrawR Con DrawR Plt 8 21 DrawR Con DrawR Plt 8 21 DrawStat 8 21 DrawWeb 8 21 Dsz Count Jump 8 17 Exp 8 25 Exp Str 8 25 For To Step Next 8 14 Getkey 8 22 Goto Lbl 8 17 If Then Else...

Page 306: ...le A Description This command momentarily interrupts program execution and prompts for input of a value or expression for assignment to a variable If you do not specify a prompt execution of this comm...

Page 307: ...arriage return only Using a carriage return in place of the multi statement command makes the displayed program easier to read Comment Text Delimiter Function Indicates comment text inserted inside a...

Page 308: ...according to the step value with each execution Execution continues until the value of the control variable exceeds the ending value Syntax For starting value control variable name To ending value St...

Page 309: ...expression Parameters expression Description This command repeats the commands contained in the loop as long as its condition is true non zero When the condition becomes false 0 execution proceeds fro...

Page 310: ...After execution of the subroutine is complete execution returns to the main routine continuing from the statement following the Prog command A Goto Lbl command inside of a subroutine is valid inside o...

Page 311: ...execution continues with the next statement If the current value is zero execution jumps to the statement following the multi statement command output command or carriage return _ Goto Lbl Function Th...

Page 312: ...t command or carriage return _ Jump Code Function This code is used to set up conditions for a conditional jump The jump is executed whenever the conditions are false Syntax True left side relational...

Page 313: ...nning jumps to the same type of label Lbl n as the one used in combination with the Goto command Specifying OK 3 for the string branch name n value or variable n part specifies a jump to Lbl 3 Example...

Page 314: ...vector name k Display Commands DISPLAY DispF Tbl DispR Tbl No parameters Function These commands display numeric tables Description These commands generate numeric tables during program execution in...

Page 315: ...vertical axis and n as the horizontal axis Description These commands graph recursion expressions in accordance with conditions defined within the program with an bn or cn as the vertical axis and n a...

Page 316: ...2 cn 2 A Memory ERROR occurs if you specify a numeric sequence name that does not have values stored in the recursion table Example PlotPhase bn 1 an 1 Graphs a phase plot using bn 1 for the x axis an...

Page 317: ...c expression string character string Description This command displays values including variable contents or text at a specific location on the text screen If there is a calculation input that calcula...

Page 318: ...d below Receive38k Send38k Function Executes data send and receive at a data rate of 38 kbps Syntax Send38k expression variable name Receive38k list name Description The OpenComport38k command must be...

Page 319: ...ugh Str 20 For details about strings see String Memory page 2 8 You can use the command page 8 27 to connect strings inside of an argument A function or command within a string function Exp StrCmp etc...

Page 320: ...r StrLen Function Returns the length of a string the number of its characters Syntax StrLen string StrLwr Function Converts all the characters of a string to lower case Syntax StrLwr string StrMid Fun...

Page 321: ...StrSrc Function Searches string 1 starting from the specified point nth character from beginning of string to determine if it contains the data specified by string 2 If the data is found this command...

Page 322: ...s described below Manual graph commands page 5 25 You can specify the color of a manual graph by placing a color command before Graph Y or any other graph commands that can be input following 4 SKETCH...

Page 323: ...2 and Using Statistical Calculations and Graphs in a Program page 8 35 k Using Paint Commands in a Program Paint commands provide you with the means to add shading to graphs The following are the two...

Page 324: ...an output command between the text and calculation Inputting more than 21 characters causes the text to move down to the next line You can specify up to 255 bytes of text for a comment k Using Matrix...

Page 325: ...dd the results to another row Row Example 3 To calculate the product of Row 2 of the matrix in Example 1 and the scalar 4 then add the result to row 3 The following is the syntax to use for this progr...

Page 326: ...x T ptch StoV Win area of V Win area 1 to 6 RclV Win area of V Win area 1 to 6 Graph Color SetG Color color command area of graph area 1 to 20 SetG Color color command element of recursion formula ele...

Page 327: ...G Pict area of picture a area 1 to 20 BG Pict folder name file name a Appending a at the end loads V Window values that are saved with the image data when the background image is displayed Syntax when...

Page 328: ...Table Graph Functions in a Program Incorporating Recursion Table Graph functions in a program lets you generate numeric tables and perform graphing operations The following shows various types of synt...

Page 329: ...stical graph Following a StatGraph command S Gph1 S Gph2 or S Gph3 you must specify the following graph conditions Graph draw non draw status DrawOn DrawOff Graph Type x axis data location list name y...

Page 330: ...gs page 6 2 The following is a typical graph condition specification for a scatter diagram or xyLine graph S Gph1 DrawOn Scatter List 1 List 2 1 Square ColorLinkOff ColorAuto In the case of an xy line...

Page 331: ...on graph S Gph1 DrawOn Sinusoidal List 1 List 2 Blue The following is a typical graph condition specification for a logistic regression graph S Gph1 DrawOn Logistic List 1 List 2 Blue The following is...

Page 332: ...s are assigned respectively to variables p ZLow and ZUp and p is assigned to Ans To draw a Student t cumulative distribution graph DrawDistT Lower Upper df Degree of freedom Data upper limit Data lowe...

Page 333: ...er Upper ndf ddf Degrees of freedom of denominator Degrees of freedom of numerator Data upper limit Data lower limit Executing DrawDistF performs the above calculation in accordance with the specified...

Page 334: ...y axis data YList x axis data XList Any one of the following can be specified as the calculation type LinearReg ax b linear regression ax b type LinearReg a bx linear regression a bx type Med MedLine...

Page 335: ...NormCD Lower Upper Single values or lists can be specified for Lower and Upper Calculation results p ZLow and ZUp are assigned respectively to variables p ZLow and ZUp Calculation result p also is as...

Page 336: ...e Syntax InvTCD p df A single value or a list can be specified for p The Lower value is assigned to the xInv and Ans variables ListAns when p is a list 2 Distribution ChiPD Returns the 2 probability d...

Page 337: ...for p The Lower value is assigned to the xInv and Ans variables ListAns when p is a list Binomial Distribution BinomialPD Returns the binomial probability p value for the specified data Syntax Binomi...

Page 338: ...ecified for p The calculation result X value is assigned to the xInv and Ans variables ListAns when p is a list Geometric Distribution GeoPD Returns the geometric probability p value for the specified...

Page 339: ...tion result X value is assigned to the xInv and Ans variables ListAns when p is a list k Using the TEST Command to Execute a Command in a Program The following are the specifications ranges for the co...

Page 340: ...ulation Syntax OneSampleTTest condition 0 o sx n OneSampleTTest condition 0 List Freq Output Values t p o sx n are assigned respectively to the variables with the same names and to ListAns elements 1...

Page 341: ...sx2 n2 Output Values F p sx1 sx2 n1 n2 are assigned respectively to the variables with the same names and to ListAns elements 1 through 6 Syntax TwoSampleFTest 1 condition List1 List2 Freq1 Freq2 Outp...

Page 342: ...iod Setting PmtBgn Start of period PmtEnd End of period Bond Calculation Payment Periods PeriodsAnnual Annual PeriodsSemi Semiannual Financial Calculation Commands For the meaning of each argument see...

Page 343: ...lment payments principal for savings Syntax Cmpd_PV n I PMT FV P Y C Y Cmpd_PMT Returns equal input output values payment amounts for installment payments deposit amounts for savings for a fixed perio...

Page 344: ...lling Price Margin Calculations Cost Returns the cost based on a specified selling price and margin Syntax Cost Sell Margin Sell Returns the selling price based on a specified cost and margin Syntax S...

Page 345: ...PowerReg_ Sin SinReg_ Logistic LogisticReg_ MAT Swap Swap_ Row Row_ Row Row _ Row Row _ LIST SortA SortA SortD SortD GRAPH SEL On G_SelOn_ Off G_SelOff_ TYPE Y Y Type r r Type Param ParamType X X Type...

Page 346: ...itV Norm Norm COMPLEX i i Abs Abs_ Arg Arg_ Conjg Conjg_ ReP ReP_ ImP ImP_ r r a bi a bi CALC Solve Solve d dx d dx d2 dx2 d2 dx2 dx SolveN SolveN FMin FMin FMax FMax logab logab Int _Int _ Rmdr _Rmdr...

Page 347: ...W h kW h ft lbf ft lbf Btu Btu erg erg kgf m kgf m POWER W W calth s calth s hp hp ft lbf s ft lbf s Btu min Btu min HYPERBL sinh sinh_ cosh cosh_ tanh tanh_ sinh 1 sinh 1 _ cosh 1 cosh 1 _ tanh 1 tan...

Page 348: ...Ymin max RightYmax scale RightYscl R T min RightT min max RightT max pitch RightT ptch FACTOR Xfct Xfct Yfct Yfct STAT X n n x x x x x 2 x2 x x sx sx minX minX maxX maxX Y y y y y y 2 y2 xy xy y y sy...

Page 349: ...ct_ DISPLAY Stat DrawStat Graph DrawGraph Dyna DrawDyna FUNCTAB Table DispF Tbl Gph Con DrawFTG Con Gph Plt DrawFTG Plt RECRTAB Table DispR Tbl Phase PlotPhase Web DrawWeb_ an Cn DrawR Con a Cn DrawR...

Page 350: ...plfyMan Q1Q3 Std Q1Q3TypeStd OnData Q1Q3TypeOnData P L CLR Plot Line Color_ key Level 1 Level 2 Level 3 Command ZOOM Factor Factor_ Auto ZoomAuto V WIN V Win ViewWindow_ Store StoV Win_ Recall RclV Wi...

Page 351: ...ata Data None None COLOR LINK BothXY ColorLinkX Y X Freq ColorLinkX Freq OnlyX ColorLinkOnlyX OnlyY ColorLinkOnlyY On ColorLinkOn Off ColorLinkOff 3 X ax b LinearReg ax b a bx LinearReg a bx 4 EXP aeb...

Page 352: ...me and file name of the specified image will be input For example Pict Pict01 g3p Level 3 Level 4 Command 9 TEST p p z z t t Chi 2 F F p p p 1 p 1 p 2 p 2 df df se se r r r2 r2 pa pa Fa Fa Adf Adf SSa...

Page 353: ...tation mark Note that non command alpha numeric characters in a program that are enclosed in quotation marks or are in a comment line are output to the text file as is Example In the program In the te...

Page 354: ...J K K L L M M N N O O P P Q Q R R S S T T U U V V W W X X Y Y Z Z _ _ a a b b c c d d e e f f g g h h i i j j k k l l Command Text m m n n o o p p q q r r s s t t u u v v w w x x y y z z Pol Pol sin s...

Page 355: ...max TThetamax T ptch TThetaptch Xfct Xfct Yfct Yfct D Start D Start D End D End D pitch D pitch RightXmin RightXmin RightXmax RightXmax RightXscl RightXscl RightYmin RightYmin RightYmax RightYmax Rig...

Page 356: ...mdr Rmdr Fa Fa n1 n1 n2 n2 x 1 x bar1 x 2 x bar2 sx1 sx1 sx2 sx2 sp Sxp p p hat p 1 p hat1 p 2 p hat2 Lower Lower Upper Upper P Y P Year C Y C Year Fb Fb F F Value z z Value p p Value t t Value se se...

Page 357: ...e DrawDyna DrawDyna DrawStat DrawStat DrawFTG Con DrawFTG Con DrawFTG Plt DrawFTG Plt DrawR Con DrawR Con DrawR Plt DrawR Plt DrawR Con DrawRSigma Con DrawR Plt DrawRSigma Plt DrawWeb DrawWeb NormalG...

Page 358: ...Off FuncOff SimulOff SimulOff AxesOff AxesOff CoordOff CoordOff LabelOff LabelOff DerivOff DerivOff LocusOff LocusOff dispOff SigmadispOff G SelOff G SelOff T SelOff T SelOff D SelOff D SelOff R SelOf...

Page 359: ...PRN Amt_PRN Amt_ INT Amt_SigmaINT Amt_ PRN Amt_SigmaPRN Cnvt_EFF Cnvt_EFF Cnvt_APR Cnvt_APR Cost Cost Sell Sell Margin Margin PmtEnd PmtEnd PmtBgn PmtBgn Bond_PRC Bond_PRC Bond_YLD Bond_YLD DateMode36...

Page 360: ...rogram accepts input of natural number A and divides it by B 2 3 5 7 to find the prime factors of A If a division operation does not produce a remainder the result of the operation is assigned to A Th...

Page 361: ...pitch step size of X Y1 Coordinate values of upper half of ellipse Y2 Coordinate values of lower half of ellipse Y3 Distances between right focus and loci Y4 Distances between left focus and loci Y5...

Page 362: ...the contents of the cell where the cell cursor is currently located When multiple cells are selected the edit box indicates the selected cell range Function menu You can enter the following types of...

Page 363: ...below to all of the cells from A1 through A999 and B1 through B430 For Type select Expression Input the following expression B1 2 A1 3 3 A1 2 4 A1 5 In this case the Spreadsheet strip of the eActivity...

Page 364: ...eate a new file and display a blank spreadsheet A new file will not be created it there is already a file with the same file name you enter in step 2 Instead the existing file will be opened u To open...

Page 365: ...dialog box that appears use f and c to move the highlighting to the file you want to import and then press w This imports the contents of the CSV file you specified to the spreadsheet Important All bl...

Page 366: ...alc function that automatically recalculates all formulas in a spreadsheet whenever you open a file or perform an editing operation in the Spreadsheet mode Auto Calc is one of the Spreadsheet setup it...

Page 367: ...l A range of cells See To select a range of cells page 9 7 An entire row of cells Move the cell cursor to column A of the row whose cells you want to select and then press d Pressing d while the cell...

Page 368: ...JUMP 5 BTM u To select a range of cells 1 Move the cell cursor to the start point of the range of cells you want to select You could select and entire row or column of cells as the start point if you...

Page 369: ...n step 1 of this procedure 3 To finalize and apply your input press w u To edit cell data 1 Move the cell cursor to the cell whose contents you want to edit 2 Press 2 EDIT 3 CELL Cell contents in the...

Page 370: ...different direction using the Move setting as described on page 1 35 2 Press 2 EDIT 5 SEQ to display the Sequence screen and then specify the function expression and values required to generate the r...

Page 371: ...start number sequence generation and input k Inputting Text into a Cell To input text make sure the first thing you input into the cell is aE The quote mark tells the calculator that what follows is t...

Page 372: ...14 k Inputting a Cell Reference Name Each cell on a spreadsheet has what is called a reference name which is derived by combining its column name A through Z with its row name 1 through 999 A cell re...

Page 373: ...ving from column B to column C one column causes A to change to B while moving from row 1 to row 3 changes two rows changes the 1 to 3 Important If the result of a copy and paste operation causes a re...

Page 374: ...nfigure the above dialog box with the following settings To specify this Perform this operation Specify the text color Press b Char Color and then use keys b through i to specify the desired color Spe...

Page 375: ...the data If you selected a range of cells in step 1 the cell you select with the cell cursor will be the upper left cell of the paste range If the location you select is within the range that you copi...

Page 376: ...UT This will go into paste standby for the selected data indicated by the 1 menu item changing to PASTE You can exit the paste standby at any time before you perform step 4 below by pressing J 3 Use t...

Page 377: ...u To input the same formula into a range of cells 1 Select the range of cells into which you want to input the same formula In this example we will assume the B1 B3 is selected See To select a range o...

Page 378: ...then press 3 DELETE This will delete the selected row s or column s immediately without displaying a confirmation message You also can perform the following steps to delete a row or column 1 Select o...

Page 379: ...ou want to cancel the insert operation at this time press J 3 Press 1 ROW to insert the applicable number of rows or 2 COLUMN to insert columns A Range ERROR occurs if an insert operation causes exist...

Page 380: ...ion 1 expression 2 or CellIf inequality expression 1 expression 2 Example CellIf A1 B1 A1 B1 Returns the value of A1 when Cell A1 value Cell B1 value Otherwise returns the value of B1 CellMin Cell Min...

Page 381: ...rod Syntax CellProd start cell end cell Example CellProd B3 B5 Returns the product of the data in cell range B3 B5 k Spreadsheet Mode Command Example This example inputs the special Spreadsheet mode f...

Page 382: ...ll they are applied starting from the lower numbered condition first If Condition1 is 0 A1 10 and Condition2 is 10 A1 20 for example both conditions are satisfied when A1 10 and the formatting specifi...

Page 383: ...ional formatting 2 Press 6 g 5 CONDIT to display the Condition screen 3 Use f and c to move the highlighting to Condition and then use the function menu to select the condition you want to configure 1...

Page 384: ...atting u Configuring Settings for Value Of Cell Type Conditions The following condition settings can be configured when Value Of Cell is selected as the condition type in step 4 under To configure con...

Page 385: ...ep 4 under To configure conditional formatting settings page 9 22 Expre Expression Use this line to directly input the conditional expression to be used for true false judgment Input rules are virtual...

Page 386: ...es ERROR Cell etc Cell stands for a single cell reference such as A1 Cell ERROR Cell BLANK Cell ERROR Cell BLANK Cell text string Cell text string u To delete conditional formatting settings 1 Select...

Page 387: ...e Normal 6 Use f to move the highlighting to Condition1 and then press 2 COND2 to display Condition2 7 Repeat steps 3 through 5 above to configure the Condition2 settings Input 1 C in the Expre line a...

Page 388: ...an operation example that is unique to the Spreadsheet mode k Example of Statistical Graph Operations GRAPH Menu Input the following data and draw a statistical graph scatter plot in this example 0 5...

Page 389: ...tion menu will appear when certain setting items are selected The number of columns you select in step 1 will determine what information is input automatically on the general graph settings screen If...

Page 390: ...o cells that define the range 4 After configuring the required settings press J or w k Example of Statistical Calculation Operation CALC Menu This example uses the data from the Drawing a Scatter Diag...

Page 391: ...ly 1 1Var XCell and 2Var XCell 2 1Var Freq and 2Var YCell 3 2Var Freq The following describes each of the setting items for this screen Item Description 1Var XCell 1Var Freq The cell range data specif...

Page 392: ...erenced in the table below For information about this menu item Refer to GRAPH GRAPH1 Statistical Graph Parameters page 6 1 GRAPH GRAPH2 GRAPH GRAPH3 GRAPH SELECT Graph Draw Non draw Status page 6 7 G...

Page 393: ...the range specified by the StatGraph screen Data1 Data2 and Data3 settings are reflected in the graph Off Same as the pie chart above When Pie is selected as the Graph Type the Pie Area setting is alw...

Page 394: ...een 7 Press 1 GRAPH1 The graph will reflect the text colors in the Category cell range A1 A5 This completes graphing with Color Link Next let s change the colors on the graph screen 8 Press 1 TRACE Th...

Page 395: ...of the selected range is stored in the specified file as List 1 the second column is saved as List 2 and so on Matrix Memory Mat A Mat Z You can store data in a range of cells that spans a multiple ro...

Page 396: ...m a specified list memory to a range of cells in a single row or a single column While the first cell of the range in a single row or single column is selected press 6 g 4 RECALL 1 LIST and then speci...

Page 397: ...cells u Example To recall data from a matrix memory to a spreadsheet 1 On the spreadsheet select the upper left cell of the range where you want the recalled data to be input 2 Press 6 g 4 RECALL 3 MA...

Page 398: ...ibution to students Students can use eActivity files to keep classroom notes memos of problems and their solutions etc 1 eActivity Overview The first thing that appears when you select the eActivity m...

Page 399: ...ic Graphs Spreadsheet or other built in applications 2 eActivity Function Menus k File List Function Menu OPEN Opens an eActivity file or folder NEW Creates a new eActivity file DELETE Deletes an eAct...

Page 400: ...movement TOP BOTTOM PageUp PageDown See page 10 6 DEL LINE DELETE Deletes the line that is currently selected or where the cursor is located INSERT Displays the following insert submenu for inserting...

Page 401: ...er Menu when a Text Line is Selected Menu when a Strip is Selected FILE Displays the following file operation submenu SAVE SAVE AS OPT CAPACITY Same as the FILE submenus under Workspace Screen Common...

Page 402: ...3 DELETE This will display a Delete eActivity confirmation message 2 Press 1 Yes to delete the file or 6 No to cancel without deleting anything u To search for a file 1 While the file menu is displaye...

Page 403: ...n back f or 6 g 1 JUMP 3 PageUp Scroll one screen forward c or 6 g 1 JUMP 4 PageDown Move the cursor to the beginning of the workspace screen 6 g 1 JUMP 1 TOP Move the cursor to the end of the workspa...

Page 404: ...while alpha text input is enabled See page 2 8 for details When upper case input is selected is displayed in the status bar and is displayed while lower case input is selected Press w to input a carr...

Page 405: ...if the cursor is located in a text line Pressing 3 CALC will change the calculation line to a text line If the cursor is located in a strip use f and c to move to the cursor to a calculation line On t...

Page 406: ...om those produced when called from a non eActivity mode u List Calculations Using the List Editor Selecting LIST on the function menu displays the List Editor List Editor operations in the eActivity m...

Page 407: ...g box that appears press the number key that corresponds to the highlighting color magenta green cyan yellow you want to use This closes the dialog box The cursor will now be the color you selected 4...

Page 408: ...o to a Text Line or Calculation Line After you append a memo to a text line or calculation line in an eActivity file you can jump to that line from the memo list Memo icon Memo list Jumping to the lin...

Page 409: ...ndow 4 Enter the text you want You can enter an explanation of the line some symbol etc You can enter up to 255 bytes of text 5 Press w This closes the memo window At this time the memo icon will appe...

Page 410: ...een like the screen shot on the right You can use either of these screens to edit memo text The detail editing screen is best when the memo contains a lot of text 3 Edit the text and then press w This...

Page 411: ...ots that are outside of the eActivity display range can be displayed by scrolling b 384 192 This is the screen size when a graph screen is saved to picture memory page 5 21 The line on the eActivity w...

Page 412: ...ve the highlighting to the image you want to insert and then press w This inserts the image with a red boundary around it The red boundary means that the image is selected u To select an image You can...

Page 413: ...gs are the way you want press J u To remove a boundary line from around an image 1 Use f and c to select the image whose boundary line you want to remove 2 Press f FORMAT c Line Color j Clear w 3 Pres...

Page 414: ...for more information Notes Run Matrix mode Matrix Editor data Matrix Editor Run Matrix mode Vector Editor data Vector Editor Equation mode simultaneous equation solution screen data Simul Equation Equ...

Page 415: ...n this example we will select Graph Graph mode graph screen data 4 Press w This will insert the type of strip you selected Graph strip in this example one line above the line where you located the cur...

Page 416: ...independent of data for modes that are entered from the Main Menu 11 Pressing w here again will display the graph screen and draw the graph based on the data saved by the strip u Notes Strips Notes is...

Page 417: ...up to 16 characters for the strip title and then press w The remainder of the existing title will disappear as soon as you input the first character Input the new title in its entirety If you want to...

Page 418: ...nd then press w u To display the strip memory usage screen 1 Use c and f to select the strip whose memory usage screen you want to view 2 Press 1 FILE 5 SIZE This will display the memory usage screen...

Page 419: ...ine picture line data etc The g2e extension is used for eActivity files other than those described above u To replace the existing file with the new version Press 1 FILE 1 SAVE to save the currently o...

Page 420: ...ty memory usage screen On the workspace screen press 1 FILE 4 CAPACITY File usage Remaining file memory capacity To exit the memory usage screen press J u To return to the file list from the workspace...

Page 421: ...s safe even when power is interrupted Normally you should use the storage memory for data you need to store securely for long periods loading data into the main memory only when you need it 1 Using th...

Page 422: ...eed to display them all divide them among multiple folders so the total number of files in a single folder is not greater than 300 Up to 200 files per folder can be displayed on the storage memory inf...

Page 423: ...p memory 1 to 99 contents Yes SDnnn E CON3 measurement memory CH1 CH2 CH3 CHSNC CHMIC CHFFT contents Yes ECON3 E CON3 current setup memory contents Yes EQUATION Equation data No F MEM Function memory...

Page 424: ...shared by applications clipboard replay history etc No TABLE Table data No FINANCE Financial mode data No V WIN V Window memory group V WIN n n 1 to 6 V Window memory No Y DATA Graph expression No Ea...

Page 425: ...ate the folder and return to the storage memory information screen This calculator supports nesting of folders up to three levels only Though you can create folders on your computer nested to more tha...

Page 426: ...on g3p g3b File 5 DETAIL or e J or d g3p g3b File 5 DETAIL or e J or d e d You can use e and d to move between the storage memory information screen file DETAIL screen and image preview screen g3p or...

Page 427: ...lect multiple files if you want 1 SELECT Selecting a group or folder also selects everything inside of it Deselecting a group or folder deselects all of its contents w If you select one or more indivi...

Page 428: ...data to the root directory To copy the data to a specific folder use f and c to move the highlighting to the desired folder and then press 1 OPEN 4 Press 1 SAVE AS This displays the file name input sc...

Page 429: ...splayed while No indicates that the copy operation is performed without any confirmation message The message Complete appears when the copy operation is complete u Error Checks During Data Copy The fo...

Page 430: ...olders see Selecting Data page 11 7 3 Press 6 DELETE 4 In response to the confirmation dialog that appears press 1 Yes to delete or 6 No to cancel the delete operation u To search for a file Example T...

Page 431: ...rt the backup A Memory Full occurs when there is not enough space available in the storage memory to complete the backup operation The following message appears if there is already backup data in the...

Page 432: ...older 4 Press w 1 A message appears to confirm whether or not you really want to restore the backed up data 1 The message No Data will appear if there is no backup data stored in the selected folder P...

Page 433: ...alculator performs storage memory optimization automatically whenever you perform a save operation and the calculator discovers storage memory is running low u To optimize the storage memory On the in...

Page 434: ...ON version 5 RESET system reset operations 6 g 1 BattSet battery settings 6 g 2 UserName user name registration 6 g 5 OS Update OS update 2 System Settings k Display Brightness Adjustment While the in...

Page 435: ...y the backlight duration 1 While the initial System mode screen is displayed press 2 PWRProp to display the Power Properties setting screen 2 Use f and c to select Backlight Duration 1 30Sec turns off...

Page 436: ...ou selected Check the contents and then press J 4 Press J or J QUIT to return to the initial System mode screen u To select the menu language 1 While the initial System mode screen is displayed press...

Page 437: ...languages and versions Menu languages and versions 3 Press J or J QUIT to return to the initial System mode screen k Reset 1 While the initial System mode screen is displayed press 5 RESET to display...

Page 438: ...for the System Language Setting page 12 3 the add in language file g3l is not deleted 2 Press the function key that corresponds to the reset operation you want to perform 3 In response to the confirma...

Page 439: ...2 3 Display Settings screen page 12 1 Power Properties screen page 12 2 Battery Settings screen shown below k Battery Settings Important Whenever you replace batteries be sure to perform the operation...

Page 440: ...yed press 6 g 2 UserName to display the user name screen 2 Press 1 EDIT If nothing is registered yet the cursor will appear in the User Name field If there is already data registered the cursor will a...

Page 441: ...splay the cursor in the Password field 3 Enter the correct password and then press w This causes a confirmation dialog box to appear 4 Press 1 Yes to delete or 6 No to cancel the delete operation k OS...

Page 442: ...fx 9860G AU PLUS fx 9750GII fx 7400GII fx 9860G Slim OS 1 11 fx 9860G SD OS 2 0 fx 9860G OS 2 0 or fx 9860G AU OS 2 0 calculator Parity PARITY NONE USB port Communication speed is in accordance with...

Page 443: ...r for data transfer See To establish a connection between the calculator and a computer page 13 3 2 ScreenRecv Mode for using the Screen Receiver software on a Windows Vista or later computer to displ...

Page 444: ...alculator USB port Running one of the following operating systems Windows Vista 32 bit SP1 or later Windows 7 32 bit 64 bit Windows 8 32 bit 64 bit Windows 8 1 32 bit 64 bit Windows 10 32 bit 64 bit M...

Page 445: ...a Personal Computer page 13 5 u To terminate the connection between the calculator and a computer 1 If the calculator is connected to a Windows computer note the drive letter E F G etc assigned to th...

Page 446: ...then try establishing a USB connection again Each group in main memory is displayed as a folder in the MainMem folder Also each data item in main memory is displayed as a file in the MainMem folder M...

Page 447: ...g affects files up to this Any folders and files past Level 3 are moved to a folder named SAVE F in storage memory Adding a g3m file to the MainMem folder while there is a USB connection between the c...

Page 448: ...group For details about the rules that govern file names and other conversion issues see Program and Text File Conversion Rules page 8 8 u To transfer data between the calculator and a computer 1 Conn...

Page 449: ...ave As to save your edits be sure to save the new file in MainMem PROGRAM Be sure to save the file in ASCII or ANSI code txt format 6 Terminate the connection between the calculator and a computer See...

Page 450: ...R message to appear on the calculator screen after you terminate the USB connection between the calculator and computer When this happens you will not be able to start up the calculator unless you per...

Page 451: ...is off 2 Connect the two calculators using the cable 3 Perform the following steps on both calculators to specify 3PIN as the cable type 1 From the Main Menu enter the Link mode 2 Press 4 CABLE This d...

Page 452: ...lays a screen for specifying the data selection method SELECT selects new data CURRENT automatically selects previously selected data 1 1 The previously selected data memory is cleared whenever you ch...

Page 453: ...g and receiving calculator look like after the data communication operation is complete Press J to return to the data communication main menu For information about the types of data items that can be...

Page 454: ...data successfully received up to the interruption will be in the memory of the receiving calculator An error occurs if the receiving calculator memory becomes full during data communication When this...

Page 455: ...PxlOn PxlOff Pxlchg and PxlTest commands are transferred as is Because of this executing a program that includes these commands on an older calculator model will result in incorrect display or a Synta...

Page 456: ...on is disabled The following table shows how each type of data is handled when transferring from an older model CASIO calculator to this calculator fx CG10 fx CG20 fx CG20 AU Data Item Description ALP...

Page 457: ...g box to appear 2 Press 4 Projector k Precautions when Connecting The icon may remain projected on the screen after you connect the calculator to a projector If this happens performing some operation...

Page 458: ...explanation of Geometry mode menus Pressing a key that corresponds to a menu 1 through 6 or K will display the menu for that tab After displaying a menu use e and d to move between menu screens To cl...

Page 459: ...ation 1 Zoom Box Enter the pan mode page 14 35 2 Pan Enter the scroll mode page 14 36 3 Scroll Enlarge the display image 4 Zoom In Reduce the size of the display image 5 Zoom Out Adjust the size of th...

Page 460: ...iangle 2 Isosc Triangle Draw a rectangle 3 Rectangle Draw a square 4 Square Draw a polygon 5 Polygon Draw a regular n gon 6 Regular n gon Draw a function graph 7 Function f x u 4 Construct To do this...

Page 461: ...the movement of the point while animation is being executed 3 Trace Display the animation editing screen 4 Edit Animation Perform an animation sequence once 5 Go once Perform an animation sequence rep...

Page 462: ...etc u To move the pointer Use the cursor keys to move the pointer around the display Holding down a cursor key moves the pointer at high speed u To make the pointer jump to a particular location Press...

Page 463: ...display a blank drawing screen u To open an existing file 1 Perform the following operation 1 File 2 Open This displays a menu of existing files Pressing 6 STRGMEM here will display the storage memor...

Page 464: ...xit the file menu press J u To save a file under a different name 1 While the file you want to save is open perform the following operation 1 File 3 Save as This will display the file name input scree...

Page 465: ...t u To open a g3p file in the Geometry mode 1 Perform the following operation 1 File 2 Open 2 Press 6 STRGMEM This displays the storage memory file list screen 3 Use c and f to move the highlighting t...

Page 466: ...Properties 5 Store Picture w Pict 1 20 2 On the Store In Picture Memory screen that appears enter a value from 1 to 20 and then press w Storing a graphic image in a memory area that already contains a...

Page 467: ...r returns to the previous menu or screen Deletes the currently selected object Page 14 32 Deselects all cancels an operation deletes all when pressed twice Displays menus Page 14 1 Selects an entire p...

Page 468: ...ing the Draw Menu Press 3 Draw to display the Draw menu You can use the Draw menu to plot points and draw line segments triangles polygons and other objects u To plot a point 1 Perform the following o...

Page 469: ...l add a point on the line at the pointer location u To draw a line segment 1 Perform the following operation 3 Draw 2 Line Segment 2 Move the pointer to the location on the display from where you want...

Page 470: ...2 Move the pointer to any location on the display and then press w 3 Move the pointer to another location on the display and then press w This will draw a ray that starts from the first point you sel...

Page 471: ...e screen and press w This will make the existing point either the center point or the circumference point u To draw an arc 1 Perform the following operation 3 Draw 7 Arc 2 Move the pointer to the loca...

Page 472: ...through the first point and the current point will appear on the display Pressing w in the following step will draw a semi circle with a diameter that forms an arc that goes counterclockwise from the...

Page 473: ...n the screen if the second point specified is too close to or at the same location of the first point u To draw an isosceles triangle 1 Perform the following operation 3e Draw Spec 2 Isosc Triangle 2...

Page 474: ...ify with the selection boundary in step 3 u To draw a polygon 1 Perform the following operation 3e Draw Spec 5 Polygon 2 Move the pointer to the location on the display where you want a vertex of the...

Page 475: ...er To draw a triangle page 14 15 This will draw a regular n gon using the number of sides you specified in step 2 u To draw a function 1 Perform the following operation 3e Draw Spec 7 Function f x Thi...

Page 476: ...rks to appear on the object At this time the object will begin to flash Note that the object will not flash if it is a point and a mark is displayed on the point 3 Press w This will cause the to chang...

Page 477: ...want to deselect This will cause the k marks to become highlighted At this time the object will begin to flash Note that the object will not flash if it is a point and a k mark is displayed on the po...

Page 478: ...the composition of the selected object 3 Configure the above dialog box with the following settings To specify this Perform this operation Specify the text color Press b Char Color and then use keys...

Page 479: ...from step 3 under To specify the color and line type of all the displayed objects page 14 21 k Using the Construct Menu Press 4 Construct to display the Construct menu You can use the Construct menu...

Page 480: ...ingle line segment and single point a single line and single point a single ray and a single point a single vector and a single point or one side of a polygon and a single point are selected on the sc...

Page 481: ...ays vector side of a polygon circle or arc u To construct an angle bisector 1 Draw a triangle and select two of its sides 2 Perform the following operation 4 Construct 5 Angle Bisector This draws the...

Page 482: ...ent and a single point a single line and a single point a single ray and a single point a single vector and a single point One side of a polygon and a single point u To construct a tangent 1 Draw a ci...

Page 483: ...ng the Transform Menu Press 5 Transform to display the Transform menu You can use the Transform menu to perform various transform operations such as object reflection object rotation etc u To reflect...

Page 484: ...ne 2 is the distance along the Y axis 4 After the values are the way you want press w This performs parallel translation of the object by the distance specified by the values you input in step 3 Note...

Page 485: ...ox for specifying the angle of rotation 5 Input the angle of rotation counterclockwise in degrees and then press w This will draw the original object rotated the specified amount Note If you select on...

Page 486: ...cedure Center of Dilation Scale 1 Scale 2 Original Object Scale 0 5 u To rotate a figure 180 degrees on a specified point 1 Draw the figure you want to rotate and select it Here we will use a triangle...

Page 487: ...ge 14 33 u To redo an operation Immediately after undoing the operation press or perform the following operation 2 Edit 1 Undo Redo k Moving and Deleting an Object Before you can move or delete an obj...

Page 488: ...ed 3 Use the cursor keys to move the object in the direction you want The rectangle will move in corresponding direction One vertex selected One side selected Three sides selected 4 To move the object...

Page 489: ...ng is selected on the screen k Hiding and Showing Objects Use the following operations to hide specific objects and to show all currently hidden objects u To hide an object 1 Select the object you wan...

Page 490: ...and grid points or grid lines on the Geometry mode screen You also can specify the pitch spacing of the grid points and lines Axes On Grid On Axes Scale Grid Line u To specify the axis and grid setti...

Page 491: ...On Length Unit On mm u To specify angle and length display units 1 Press m SET UP to display the Setup screen 2 Perform the following operations to configure the settings you want To select this sett...

Page 492: ...settings to their initial defaults press 1 INITIAL 3 After all the settings are the way you want press J k Using Pan and Scroll to Shift the Display Image There are two methods available for shifting...

Page 493: ...ection you want 3 To exit the Scroll mode press J k Zooming The Geometry mode provides you with a selection of zoom commands that you can use to enlarge or reduce an entire screen image or a specific...

Page 494: ...is open in the Geometry mode To adjust image lightness press K Option e Properties 4 Fade I O and then perform the procedure from step 2 under To adjust the lightness Fade I O of the background image...

Page 495: ...on on the screen if you want For details see To move an object page 14 30 u To edit screen text 1 Select the text you want to edit 2 Press J This displays the measurement box at the bottom of the scre...

Page 496: ...this example we will select point A 2 Press J This displays the measurement box at the bottom of the screen 3 Press d to highlight the up arrow button on the left side of the measurement box and then...

Page 497: ...d to highlight the up arrow button on the left side of the measurement box and then press w This displays an icon palette 4 Use the cursor keys to move the highlighting to the icon on the icon palett...

Page 498: ...You can specify the coordinates of a point the length of a line segment distance between endpoints the angle formed by two lines etc Lock the measurement of part of an object After you display the me...

Page 499: ...pression EXPR object Calculation formula No Vector A single vector Vector components Yes Radius A single circle semi circle or arc Radius of circle semi circle or arc Yes Circumference A single circle...

Page 500: ...Text A point that has a label or an object that can be named Label text No You can use the measurement box to determine certain measurements The first example below shows how to view the measurements...

Page 501: ...ermine the areas of the triangles formed by points A D and B and points A D and C 1 Draw the rectangle 2 Select points A D and B 3 Press J This causes the area of the triangle ADB to appear in the mea...

Page 502: ...ify the angle of a triangle and the length of one side of a triangle u To specify the angle of a triangle 1 Draw a triangle 2 Select side AC and then select side BC 3 Press J to display the measuremen...

Page 503: ...area Length of one side of a triangle Length of a line segment or vector Length of one side of a rectangle square polygon or regular n gon Circumference of a circle or length of an arc View Window set...

Page 504: ...is unlocked Measurement is locked u To lock a particular measurement You can lock a particular measurement by performing any one of the following operations Perform the procedure under Specifying a M...

Page 505: ...you locked manually as well as objects that are locked automatically whenever they are drawn For example the above operation unlocks all of the following lock conditions The lock that is applied when...

Page 506: ...perimeter area angle supplementary angle u To paste a measurement into a screen image Example To paste an internal angle measurement into a screen image 1 Draw a triangle and select two of its sides 2...

Page 507: ...e Tag When you paste a measurement into a screen image using the To paste a measurement into a screen image procedure on page 14 49 a measurement type tag text or a symbol is appended in front of the...

Page 508: ...perform calculations using the angle value line length and other measurement values attached to an object and display the result on the screen u To display the result of a calculation that uses on scr...

Page 509: ...asurement box input the at sign followed by the numeric label of the value 1 2 etc Since we want to calculate the sum of angles DCB 1 and ACD 2 here you would input the following 1 2 You can input by...

Page 510: ...ce area of displayed figures Example To calculate the sum of the surface areas of two displayed triangles and display the expression and calculation results 1 Draw the triangles and then specify blue...

Page 511: ...ide of the screen 2 DA B C appears on the right triangle and 2 the symbol for DA B C is input into the measurement box 6 Press w This causes the calculation expression DABC DA B C to appear at the top...

Page 512: ...r format setting integer values are always displayed with their decimal parts cut off u To specify the number format of a measurement Example To specify one decimal places for measurement values 1 Sel...

Page 513: ...tion u To add an animation and run it Example To animate a point around a circle 1 Plot a point and draw a circle and select them 2 Perform the following operation 6 Animate 1 Add Animation This will...

Page 514: ...Go once or 6 Animate 6 Go repeat 4 To stop the animation press J or o u To trace a locus of points Note Using trace leaves a trail of points when the animation is run Example To use the Trace command...

Page 515: ...nd DC and then press J 9 Press dw to display the icon palette move the highlighting to the icon and then press w w 10 Use e to move the highlighting to the icon and then press w This changes the icon...

Page 516: ...off or manually while an animation is being performed the animation will be stopped u To edit an animation Example While the animation screen created with the procedure under To trace a locus of point...

Page 517: ...which is located just under the E of Animations 2 Input a number from 10 to 10 t0 specifies the start point for point E movement along line segment AB Inputting a value of 0 specifies point A as the s...

Page 518: ...m under Animations screen Note Selecting Animations in step 1 and then pressing 1 DELETE will delete the animations assigned to all points Turn off trace for point D 1 Use c and f to move the highligh...

Page 519: ...ated on horizontal line AB Next generate an animation table that includes the length of line segment CD and the area of the triangle as point D moves along line segment AB 1 Draw line segment AB and t...

Page 520: ...on palette that appears select the icon 11 Perform steps 5 through 6 above Now when the animation table appears it will include the Length column we created in step 6 long with a new Area column which...

Page 521: ...bout list data see Chapter 3 List Function u To save an entire animation table as spreadsheet data 1 Display the animation table 2 Press 1 STORE 2 S SHT This displays a dialog box for inputting the sp...

Page 522: ...int on the path traced by the water as a coordinate X Y The Picture Plot plot function makes it easy to plot points on a photograph such as this or some other image and extract the coordinate values o...

Page 523: ...re in the Graph mode k Picture Plot Specific Setup Items The items described below are Picture Plot specific Setup screen items that appear only after you press m SET UP indicates default setting Axtr...

Page 524: ...de page 5 36 AXTRNS Displays the following submenu T Y T X Splits the screen in half left and right and specifies horizontal axis T vertical axis Y horizontal axis T vertical axis X for the right side...

Page 525: ...ta to the Plot List X column or Y column k Plot Mode Function Menu PICTURE Same as PICTURE under Picture Plot Screen Function Menu UNDO Deletes the last point plotted Executing UNDO again will plot th...

Page 526: ...ess you want to change to another image file or reset the calculator u To open a file 1 From the Main Menu enter the Picture Plot mode This displays the file list screen If the file you opened the las...

Page 527: ...the setting of the file that was opened the last time you were in the Picture Plot mode will be recalled For V Window settings the settings stored with a file will be recalled whenever the file is op...

Page 528: ...plots k Plotting Points u To plot points on the screen 1 Enter the Picture Plot mode and then open a g3p or g3b file This displays the Picture Plot screen For information about how to open a file see...

Page 529: ...to jump to the corresponding section of the screen as shown below h i j e f g b c d u Plotting Points in a g3b File A g3b file is a special Picture Plot file that can contain up to 30 images in a sing...

Page 530: ...ve the plot and then press w This will move the plot The pointer will move to the next sequential plot when there is one If you want to move another plot repeat steps 2 and 3 4 After you are finished...

Page 531: ...ith the Graph mode Note however that only Y type graphs can be used in the Picture Plot mode Because of this calling up the graph relation list screen from the Picture Plot mode will display a Y Y typ...

Page 532: ...ression Type page 6 16 2 For information about the meanings of the values that appear on this screen see Displaying Regression Calculation Results page 6 17 and the regression graph explanations on pa...

Page 533: ...ptimum viewing of plots and graphs Note that the lightness setting can be adjusted only when the image is a 16 bit image data After you adjust the lightness level the setting is stored in the image fi...

Page 534: ...alue indicates time For more information about T values see Displaying Plots on T Y Coordinates and T X Coordinates AXTRANS Screen on page 15 14 On this screen you can edit the X and Y values only 2 U...

Page 535: ...Displaying Plots on T Y Coordinates and T X Coordinates AXTRANS Screen As can be seen on the plot list screen the data for each plot includes X and Y coordinates as well as a time value T On the Pictu...

Page 536: ...he T value has changed as you intended Note The following are the ranges for the start value and the step value 1 0E 10 Start 1 0E 10 0 Step 1 0E 10 u To display plots on T Y coordinates or T X coordi...

Page 537: ...the display mode of the left side X Y coordinate system of the AXTRANS screen below Go to the plot list screen 3 List Draw a regression graph overlaid on the plots in the right side screen 4 REG From...

Page 538: ...eft side and right side of the AXTRANS screen that correspond to each other to flash 1 While the AXTRANS screen is on the display press K5 P LINK This will cause the plots on the left side X Y coordin...

Page 539: ...ently located Perform the following steps to change the plot color 1 While the Picture Plot screen contains plotted points press 1 TRACE This causes a trace pointer to appear at the first point that w...

Page 540: ...integer value in a location that requires integer input Input an integer value Input value must be a matrix Attempting to input a non matrix value in a location that requires matrix input Input a mat...

Page 541: ...ct the input expression Time Out A Solve calculation was unable to satisfy convergence conditions If you are performing a Solve calculation try changing to the initial default estimated value Conversi...

Page 542: ...nge all data in the matrix to real numbers Complex Number In Matrix or Vector Matrix or vector containing complex number used in a calculation or operation for which complex number data is invalid Cha...

Page 543: ...hat is being used for graphing is located Select a different area and try again Requires one variable expression You attempted to execute a Modify function operation while no expression that contains...

Page 544: ...cify a list other than the one being used for the Test Confidence Interval or Distribution calculation Program errors When you see this message It means this So you need to do this Go ERROR 1 No corre...

Page 545: ...he eActivity mode file menu screen pressing 5 MEMO while a file that does not include a MEMO is selected Attempting to display the MEMO Catalog screen while editing a file that does not include a MEMO...

Page 546: ...displayed and it contains a level 4 nested folder The level 4 folder will be displayed but it cannot be opened Use your computer 1 to store all files you want to access in the top three folder nestin...

Page 547: ...eration as described in Reset page 12 4 Important Performing an Initialize All operation will delete all data in calculator memory including language data If you need the data in calculator memory use...

Page 548: ...wrong with the cable connection and that parameters are configured correctly Transmit ERROR Problem with cable connection or parameter setting during data communication Check to make sure there is not...

Page 549: ...ect 2 segments You are trying to construct an angle bisector without first selecting two line segments Too Many Objects Work memory cleared Work memory became full Delete objects you no longer need or...

Page 550: ...imation because it is already being used in the animation you are configuring or in another animation Select a point to which animation can be added and try again Select the applicable measurement ico...

Page 551: ...n the Recursion mode when the Start value is greater than or equal to the End value The Edit Animations screen is configured with the setting t0 t1 in the Geometry mode Internal calculation generated...

Page 552: ...Picture Memory number Specify a Picture Memory number where a file is stored Not Enough Elements The list you specified for a calculation does not contain the number of elements required to perform th...

Page 553: ...x cosh 1 x tanh 1 x x 1 10100 1 x 1 10100 x 1 logx lnx 1 10 99 x 1 10100 Complex numbers can be used as arguments 10x ex 1 10100 x 100 Complex numbers can be used as arguments 1 10100 x 230 2585092 x...

Page 554: ...lation error is 1 at the 10th digit In the case of exponential display calculation error is 1 at the last significant digit Errors are cumulative in the case of consecutive calculations which can also...

Page 555: ...E CON3 Application English...

Page 556: ...asurement functions of the CASIO EA 200 Data Logger Though it can run on a CMA CLAB Data Logger CLAB does not have a SONIC port microphone or speaker as is equipped on the EA 200 While a calculator is...

Page 557: ...G10 fx CG20 fx CG20 AU It also can be used to convert data to a program that can be run on a CFX 9850 Series fx 7400 Series calculator 4 START Starts data collection 5 GRAPH Graphs data sampled by a D...

Page 558: ...setup using Setup Wizard Note To terminate Setup Wizard part way through and cancel the setup press J QUIT 1 Display the E CON3 main menu page 1 2 Press 1 SET and then 1 WIZARD This launches the Setu...

Page 559: ...gate alone on page 5 VERNIER Photogate Pulley or CMA Photogate Pulley To configure a setup for Photogate and Smart Pulley on page 5 CASIO Speaker y f x Outputting the Waveform of a Function through th...

Page 560: ...ions for the sampled sound data elapsed time horizontal axis and volume vertical axis FFT records the following two dimensions frequency horizontal axis and volume vertical axis The following shows th...

Page 561: ...ontinues until it closes 3 Close Open Timing starts when the gate closes and continues until it opens 4 Close Close Timing starts when the gate closes and continues until it opens and then closes agai...

Page 562: ...on page 2 3 On the Select Sensor screen select CASIO Speaker y f x This displays a screen like the one shown nearby 4 Press w to advance to the View Window setting screen The following settings are c...

Page 563: ...or some reason the message Range Error will appear If this happens press J to scroll back through the previous setting screens and change the setup as required 12 To terminate sound output press the E...

Page 564: ...have stored in memory can be selected using Channel in step 5 below 5 Use the Advanced Setup keys described below to set other parameters b Channel Displays a screen that shows the sensors that are c...

Page 565: ...Perform the following procedure when you want to return the parameters of the setup in the current setup memory area to their initial defaults 1 While the Advanced Setup menu page 8 is on the display...

Page 566: ...r menu you can press the K key to toggle smoothing correction of measurement error on Smooth displayed and off Smooth not displayed From the menu that appears after you select Photogate as the sensor...

Page 567: ...ed which indicates that you can select the sampling mode 2 Select the sampling mode that suits the type of sampling you want to perform To do this Press this key To select this mode Graph data in real...

Page 568: ...display a dialog box for specifying the number of samples The total sampling time shown at the bottom of the dialog box is calculated by multiplying the Sampling Interval value you specified in step...

Page 569: ...aracteristic graphing FFT Graph on and off To do this Press this key Turn on graphing of frequency characteristics after sampling 1 On Turn off graphing of frequency characteristics after sampling 2 O...

Page 570: ...lways EXE key when the sampling mode is Extended and CH1 when the sampling mode is Clock or Period 3 Perform one of the following operations in accordance with the trigger source that was selected in...

Page 571: ...n to the Advanced Setup menu page 8 To specify the trigger threshold value and trigger edge type Perform the following steps when Fast Normal or Clock is specified as the sampling mode page 11 1 Move...

Page 572: ...d Edge 7 Press one of the function keys described below To select this type of edge Press this key Falling 1 Fall Rising 2 Rise 8 Press w to finalize Trigger Setup and return to the Advanced Setup men...

Page 573: ...is complete You use the Sample Setup settings page 11 to turn graphing on or off To configure Graph Setup settings 1 While the Advanced Setup menu page 8 is on the display press e Graph This displays...

Page 574: ...display setting use the f and c cursor keys to move the highlighting to Econ Axes Next press one of the function keys described below To specify this axes display setting Press this key Display axes 1...

Page 575: ...lts To configure a custom probe setup 1 From the E CON3 main menu page 1 press 1 SET and then 2 ADVANCE to display the Advanced Setup menu 2 On the Advanced Setup menu page 8 press f Custom Probe to d...

Page 576: ...pare two conditions whose measurement values are known When inputting reference value in step 5 of the procedure below input the exact known measurement value of the condition you will sample in step...

Page 577: ...ically and display the same type of screen that appeared in step 3 Second sampling operation 6 After the sampled value stabilizes hold down w for a few seconds This will register the second sampled va...

Page 578: ...cedure If you are editing the configuration of an existing custom probe 1 On the Custom Probe List use the f and c cursor keys to highlight the name of the custom probe you want to edit and then press...

Page 579: ...age 8 use the Channel Setup screen page 9 to configure sensor setups for each channel you will be using 3 After configuring the sensor setups press w to return to the Advanced Setup menu page 8 and th...

Page 580: ...e function key operations described below If the Advanced Setup menu page 8 is on the display press 3 MEMORY If the E CON3 main menu page 1 is on the display press 2 MEMORY Performing any one of the a...

Page 581: ...for sampling Be sure to perform the following steps before starting sampling with a Data Logger 1 Connect the calculator to a Data Logger 2 Turn on Data Logger power 3 In accordance with the setup yo...

Page 582: ...e confirmation message that appears press 1 Yes to delete the setup To clear the confirmation message without deleting anything press 6 No To recall setup data Recalling setup data stores it in the cu...

Page 583: ...the display The program converter procedure is identical in all of the above cases To convert a setup to a program 1 Start the converter operation by performing one of the key operations described be...

Page 584: ...Data Logger Perform this key operation EA 200 2 TYPE 1 200 EA 100 2 TYPE 2 100 The number part of the Data Logger model number you specify will appear in line F2 of the program converter screen Impor...

Page 585: ...Series Convert EA 200 Control Program for fx 9860G Series fx CG10 fx CG20 fx CG20 AU To convert a program 1 Transfer the EA 200 control program created for the CFX 9850 Series to the fx CG10 fx CG20 f...

Page 586: ...ing a new setup with Setup Wizard page 2 After configuring a new setup with Advanced Setup page 8 While the E CON3 main menu page 1 is on the display While the setup memory list is on the display The...

Page 587: ...g The screens that appear while sampling is in progress and after sampling is complete depend on setup details sampling mode trigger setup etc For details see Operations during a sampling operation be...

Page 588: ...w Mode Real time Fast Normal Sound Extended Period Clock 1 Data Logger Setup 2 Start Standby 3 Sampling 4 Graphing w The screen shown below appears when CH1 SONIC or Mic is used as the trigger Pressin...

Page 589: ...d by a new sampling operation save the data in sample data memory under a different file name k Managing Sample Data Files To save current sample data to a file 1 On the E CON3 main menu page 1 press...

Page 590: ...mber file name If you specify a memory number that is already being used to store a data file a confirmation message appears asking if you want to replace the existing file with the new data file Pres...

Page 591: ...appears after you perform a sampling operation Press 5 GRAPH at that time When you access Graph Analysis tools using this method you can select from among a variety of other Analysis modes See Select...

Page 592: ...nu that appears To do this Perform this menu operation To select this mode Graph three sets of sampled data simultaneously Norm Graph Analysis Graph sampled data along with its first and second deriva...

Page 593: ...three graphs If you select Compare Graph as the analysis mode in step 2 you must specify sample data files for two graphs With other modes you need to specify only one sample data file For details ab...

Page 594: ...On the Graph Mode screen press 6 DRAW or w This draws the graph s in accordance with the settings you configured in step 2 through step 6 Graph Screen When a Graph screen is on the display the functio...

Page 595: ...menu of special View Window commands for the E CON3 mode graph screen For details about each command see Configuring View Window Parameters on page 49 4 SKETCH Displays a menu that contains the follow...

Page 596: ...rsor keys k Using Trace Trace displays a crosshair pointer on the displayed graph along with the coordinates of the current cursor position You can use the cursor keys to move the pointer along the gr...

Page 597: ...to the item you want to change and then press the applicable letter key 5 After everything is the way you want press w This stores the values and exits the trace operation For details about using Alph...

Page 598: ...To transform sampled data to list data 1 On the graph screen press K and then 2 LISTMEM This displays the LISTMEM menu 2 Press 2 SELECT This displays the trace pointer for selecting the range on the g...

Page 599: ...n is effective for studying sounds by expressing them as functions The procedure below assumes that there is a graph of sampled sound data already on the graph screen To perform Fourier series expansi...

Page 600: ...correctly with the original graph on which it is overlaid If this happens shift the position the original graph to align it with the overlaid graph For information about how to move the original grap...

Page 601: ...DRAW This draws a quadratic regression graph and overlays it over the original graph To delete the overlaid quadratic regression graph press 4 SKETCH and then 1 Cls k Overlaying a Y f x Graph on a Sa...

Page 602: ...e EDIT menu appears at the bottom of the display 2 Press 1 ZOOM This displays only one of the graphs that were originally on the graph screen 3 Use the f and c cursor keys to cycle through the graphs...

Page 603: ...o exit the zoom mode press J To move a particular graph on a multi graph display 1 When the graph screen contains multiple graphs press K and then 3 EDIT This displays the EDIT menu 2 Press 2 MOVE Thi...

Page 604: ...end point an output frequency dialog box shown below appears on the display 4 Input a percent value for the output frequency value you want The output frequency specification is a percent value To out...

Page 605: ...owing View Window parameters Y axis Elements In accordance with screen size X axis Elements In accordance with screen size when 1 data item equals 1 dot 1 data equals 1 dot in other cases 2 FULL Resiz...

Page 606: ...he applicable strip This means that the next time you open the strip sampling can be performed in accordance with the previously configured setup information Econ Sampling strip This strip executes Da...

Page 607: ...ufacturer CASIO COMPUTER CO LTD 6 2 Hon machi 1 chome Shibuya ku Tokyo 151 8543 Japan Responsible within the European Union Casio Europe GmbH Casio Platz 1 22848 Norderstedt Germany www casio europe c...

Page 608: ...6 2 Hon machi 1 chome Shibuya ku Tokyo 151 8543 Japan One or more of the following patents may be used in the product U S Pats 5 901 074 7 927 221 8 214 413 8 576 230 8 817 027 9 007 376 SA1511 G 2013...

Reviews:

No comments

Brands by name

Popular brands

Load more brands