Casio CFX-9970G, Руководство пользователя

Страница: 120 / 474

94
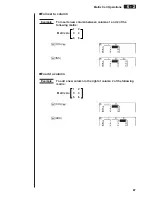
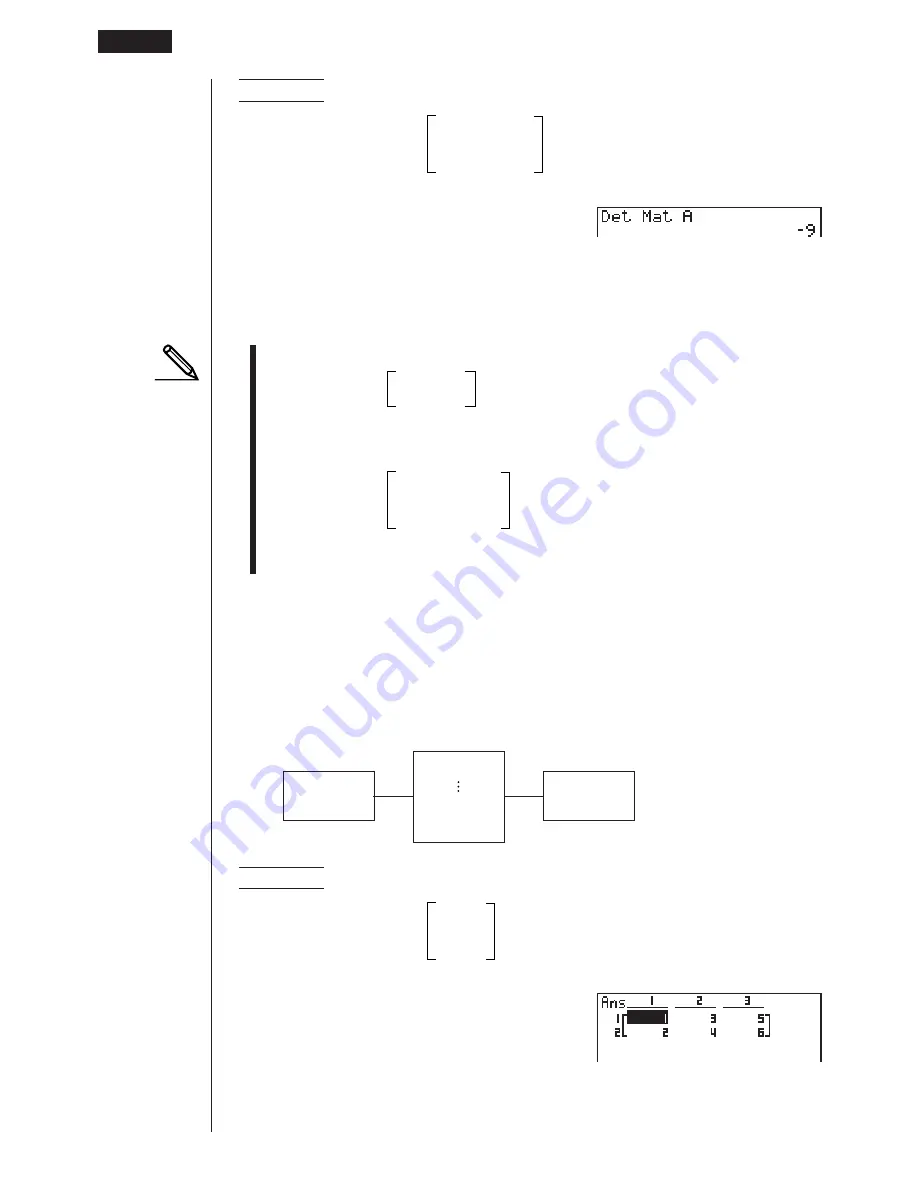
Example Obtain the determinant for the following matrix :
1 2 3
Matrix A = 4 5 6
–1 –2 0
3
(Det)
1
(Mat)
a A w
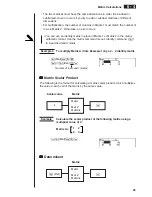
• Determinants can be obtained only for square matrices (same number of rows
and columns). Trying to obtain a determinant for a matrix that is not square
produces an error.
• The determinant of a 2
!
2 matrix is calculated as shown below.
| A | =
a
11
a
12
= a
11
a
22
– a
12
a
21
a
21
a
22
• The determinant of a 3
!
3 matrix is calculated as shown below.
a
11
a
12
a
13
| A | = a
21
a
22
a
23
a
31
a
32
a
33
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
– a
11
a
23
a
32
– a
12
a
21
a
33
– a
13
a
22
a
31
k k k k k
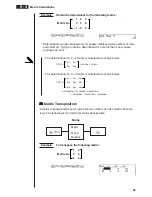
Matrix Transposition
A matrix is transposed when its rows become columns and its columns become
rows. The following is the format for matrix transposition.
Matrix
Mat A
4 (Trn) w
Mat Z
MatAns
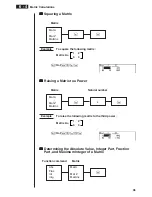
Example To transpose the following matrix :
1 2
Matrix A = 3 4
5 6
4 (Trn) 1 (Mat) a
A
w
6 - 4
Matrix Calculations