63
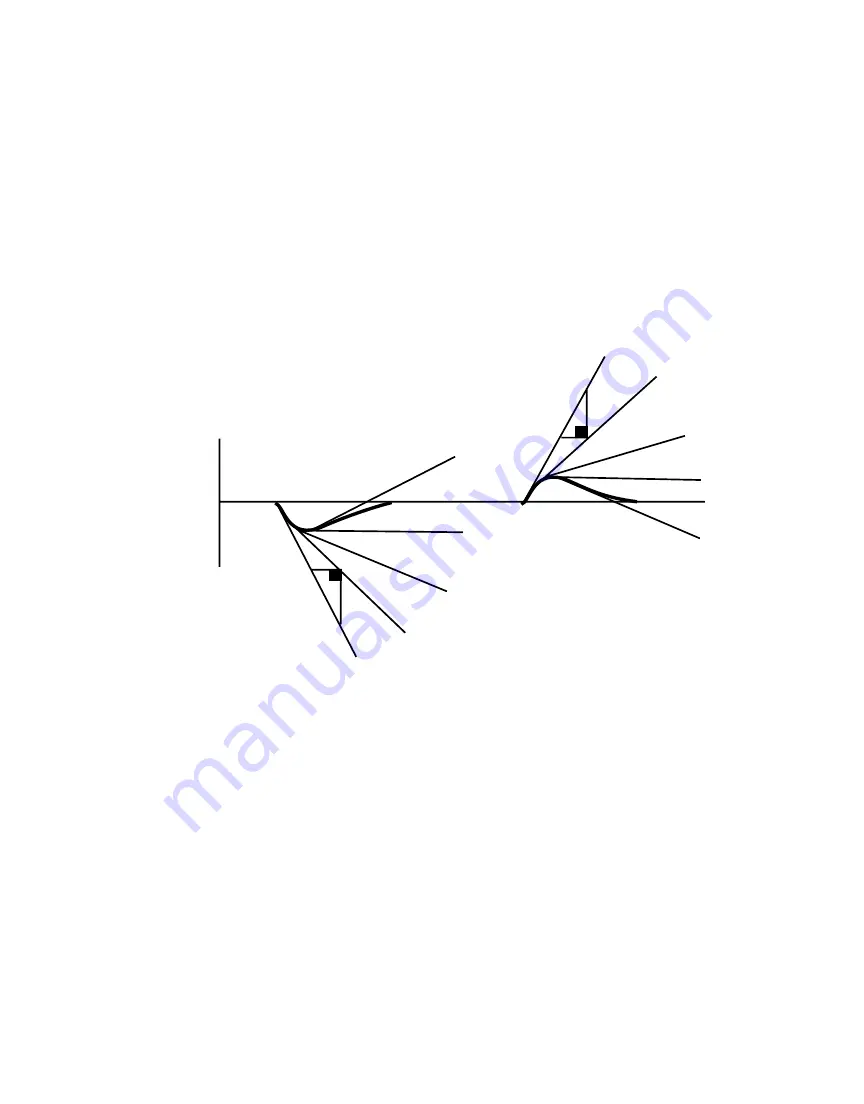
The derivative action changes the rate of reset or integration propor-
tional to the rate of change and lag time of the system. By calculating
the rate of change of the process and multiplying it by the lag time
which is the time it takes the controller to sense an output change, the
controller can anticipate where the process should be and change the
output accordingly. This anticipatory action speeds up and slows down
the effect of proportional and proportional-integral actions to return a
process to setpoint as quickly as possible with minimum overshoot. See
the diagram below.
Derivative time is the amount of anticipatory action needed to return a
process back to setpoint. A short derivative time means little derivative
action. If the derivative time is too short, the controller would not react
quickly to process disturbances. A long derivative time means more
derivative action. If the derivative time is too large, the controller would
react too dramatically to process disturbances creating rapid process
oscillation. A process which is very dynamic such as pressure and flow
applications is more efficiently controlled if the derivative action is
turned off because of the oscillation problem that would result.
PV
Time
Rate of Change X Lag Time=
Anticipated Process Variable














































