13
4
CONFIGURATION…
4.4
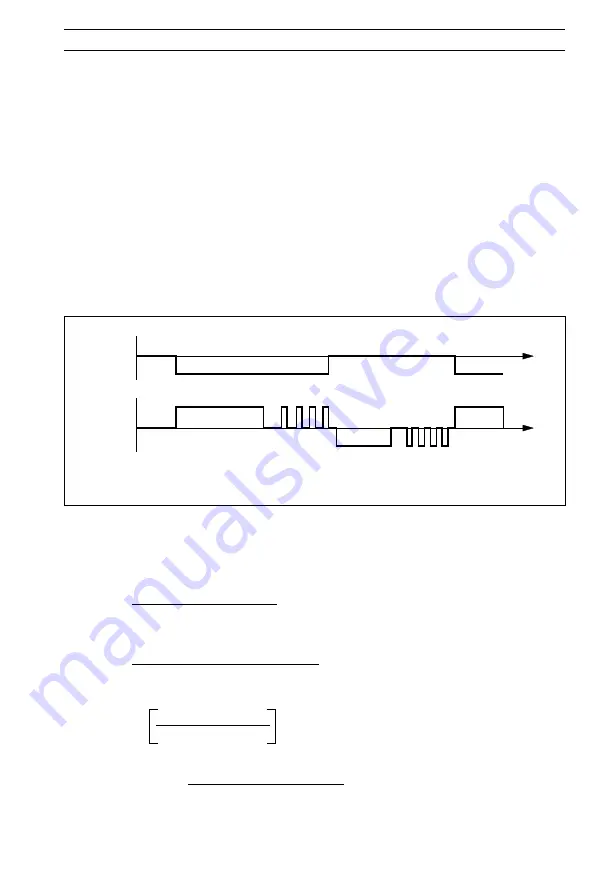
Motorized Valve Control without Feedback (Boundless) – Fig. 4.3
A 'boundless' process controller provides an output that is effectively the time derivative of the
required regulator position, i.e. the controller signals the regulator, not where to go to (position
derivative), but in which direction to travel and how far to move, by a series of integral action
pulses. Thus, the controller does not need to know the absolute regulator position and is
unaffected when regulator reaches the upper or lower limit, as determined by the regulator's
limit switches (giving rise to the term 'boundless').
In this system, the final regulator must act as an integrator, integrating both the raise and lower
pulses in direction and duration so that the final position of the regulator reproduces the
required 2 or 3 term control function, and must remain stationary indefinitely in the absence of
raise or lower commands.
When a deviation from set point is introduced the regulator is driven, for a length of time
equivalent to the proportional step. The regulator is then driven by integral action pulses until
the deviation is within the deadband setting.
4.4.1
Calculation for Control Pulses,
Steps and Deviation (Boundless Control only)
Minimum 'ON' time of integral action pulses (for a fixed control deviation).
=
Travel Time x Deadband %
% Proportional Band
(in seconds)
Minimum (approximate) time between integral action pulses (for a fixed control deviation)
=
Integral Action Time x Deadband %
2 x % Control Deviation
(in seconds)
Duration of the proportional step
= 2 x
% Control Deviation
% Proportional Band
x Travel Time in Seconds
% Control Deviation =
Set Point – Process Variable
Span
Fig. 4.3 Boundless Control Action
Proportional
Step
Time
Control
Deviation
Raise
Lower
Time
Integral
Action Pulses
Proportional
Step
Proportional
Step
Integral
Action Pulses
+
–
Artisan Technology Group - Quality Instrumentation ... Guaranteed | (888) 88-SOURCE | www.artisantg.com
















































