Chapter 13: Inferential Statistics and Distributions
245
c
2
pdf(
x
,
df
)
Note:
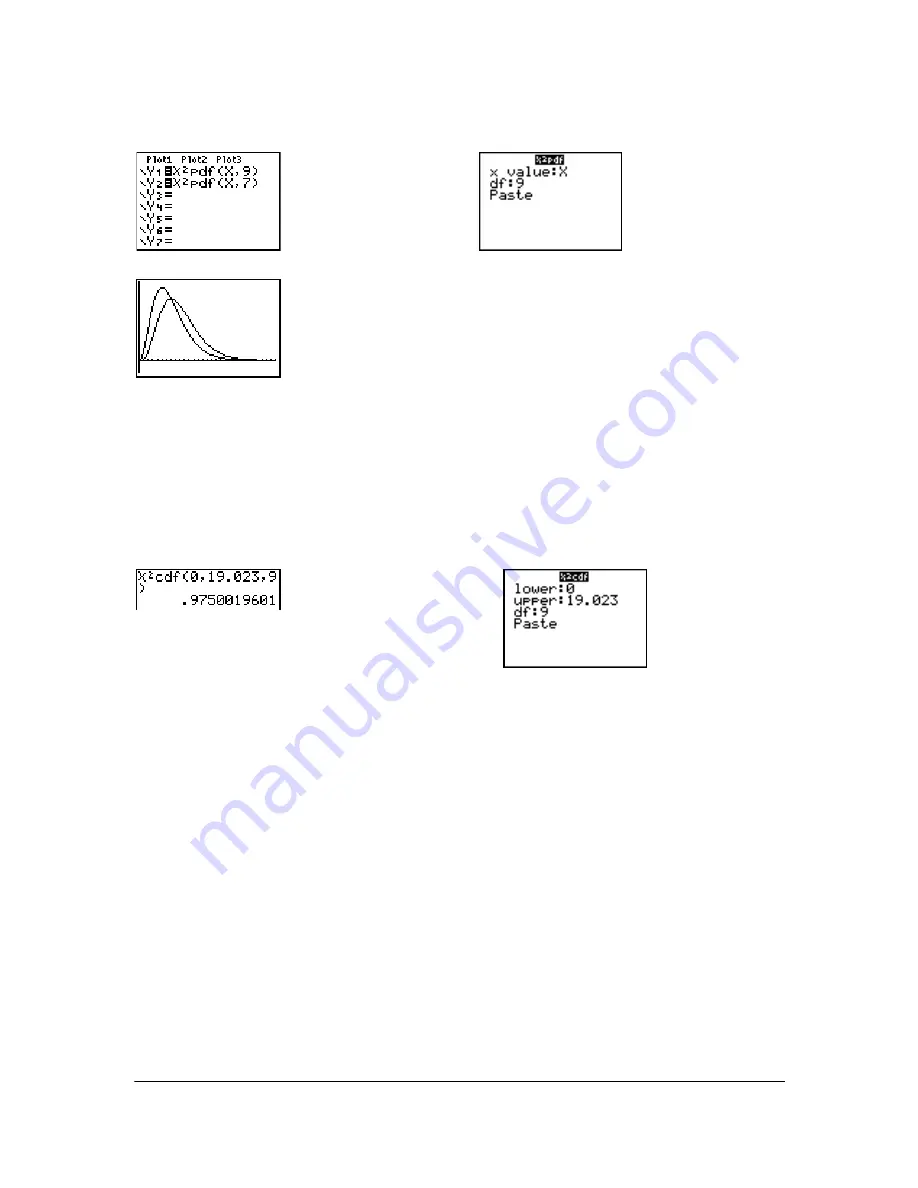
For this example,
Xmin = 0
Xmax = 30
Ymin =
L
.02
Ymax = .132
c
2
cdf(
c
2
cdf(
computes the
c
2
(chi-square) distribution probability between
lowerbound
and
upperbound
for
the specified
df
(degrees of freedom), which must be an integer > 0.
c
2
cdf(
lowerbound
,
upperbound
,
df
)
f x
( )
Γ
n d
+
(
)
/2
[
]
Γ
n
/2
(
)Γ
d
/2
(
)
----------------------------------
n
d
---
⎝ ⎠
⎛ ⎞
n
/2
x
n
/2 1
–
1
nx
/
d
+
(
)
n d
+
(
)
/2
–
x
0
≥
,
=
Fpdf(
Ü
pdf(
computes the probability density function (
) for the
Ü
distribution at a specified
x
value.
numerator df
(degrees of freedom) and
denominator df
must be integers > 0. To plot the
Ü
distribution,
paste
Ü
pdf(
to the Y= editor. The probability density function (
) is:
where
n
= numerator degrees of freedom
d
= denominator degrees of freedom
















































