Harmonic Drive SHA CG Series, Manual

Page: 103 / 109

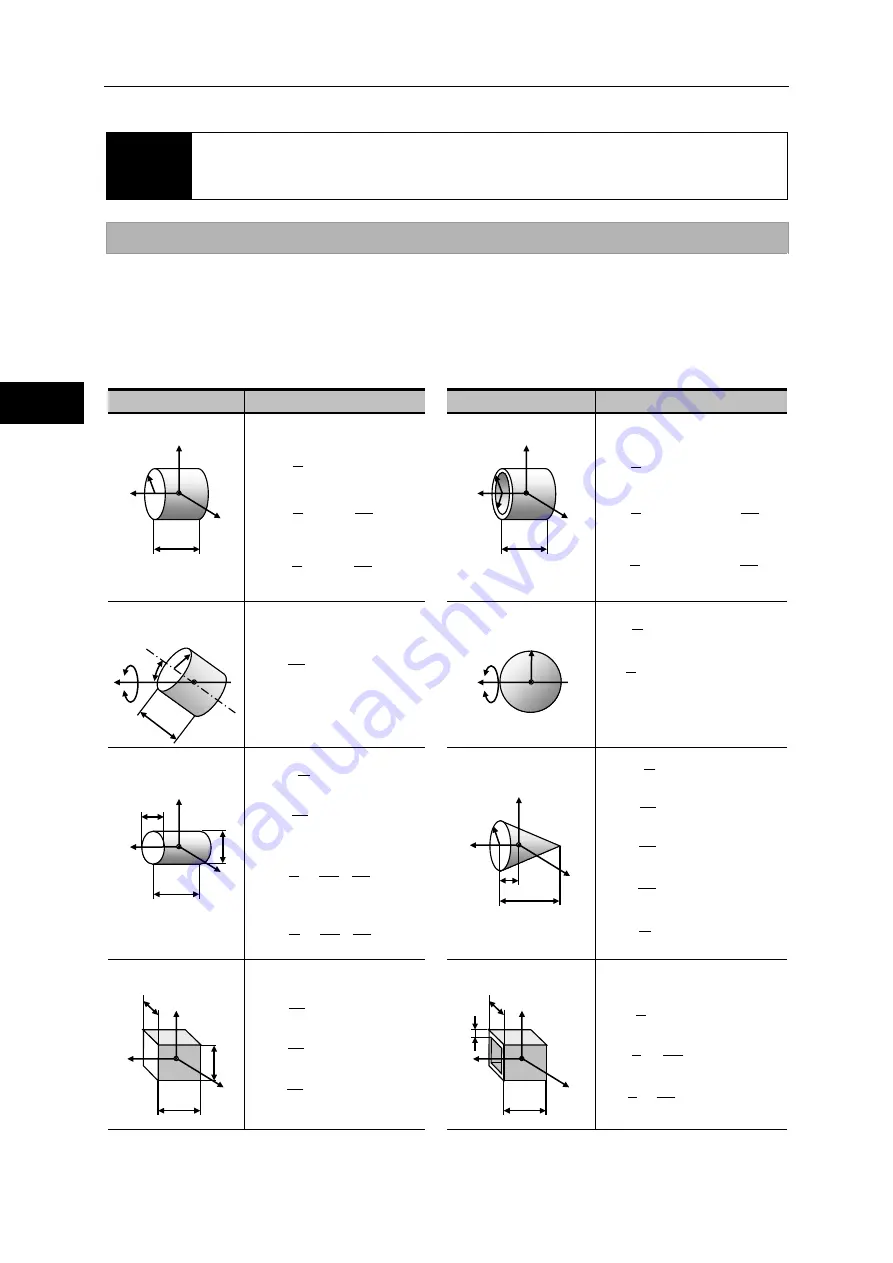
Calculating moment of inertia
103
1
2
3
4
Apx
6
7
8
9
10
11
付
A
ppe
ndi
x
4-3 Calculating moment of inertia
Formula for moment of inertia and mass
(1) For cases where the center of gravity is coincident with the axis of rotation:
The following table includes formulas to calculate mass and inertia moment.
m : mass (kg), Ix, Iy, Iz: inertia moments which rotates around x-, y-, z-axes respectively (kg
･
m 2 )
G : distance from end face of gravity center (m)
ρ
: specific gravity
Unit Length: m, Mass: kg, Inertia moment: kg
･
m
2
Object form Mass, inertia, gravity center Object form Mass, inertia, gravity center
Cylinder Circular pipe
Slanted cylinder Ball
Ellipsoidal cylinder Cone
Rectangular pillar Square pipe
A
R
L
z
x
y
ρ L R m
2
π =
2
R m
2
1
Ix
=








+ =
3
L
R m
4
1
Iy
2
2








+ =
3
L
R m
4
1
Iz
2
2
R
1
L
R
2
z
x
y
R
1
: Outer diameter
R
2
: Inner diameter
( )
ρ π L R R m
2
2
2
1
− =
( )








+ + =
3
L
R R m
4
1
Iy
2
2
2
2
1
( )
2
2
2
1
R R m
2
1
Ix + =
( )








+ + =
3
L
R R m
4
1
Iz
2
2
2
2
1
B
L
z
x
y
C
ρ L BC m
4
1
=
( )
2 2
C B m
16
1
Ix
+ =








+ =
3
L
4
C
m
4
1
Iy
2 2








+ =
3
L
4
B
m
4
1
Iz
2 2
R
L
z
x
y
G
ρ π
1
L R
3
m 2
=
2
R m
10
3
Ix
=
( )
2 2
L 4R m
80
3
Iy
+ =
(
)
2 2
L 4R m
80
3
Iz + =
4
L
G =
z
x
y
C
B
A
ρ
A
BC m
=
(
)
2 2
C B m
12
1
Ix + =
( )
2 2
A C m
12
1
Iy
+ =
(
)
2 2
B A m
12
1
Iz + =
D
B
A
z
x
y
( )
ρ
D - B 4AD
= m
( )
{ }
2 2
D D - B m
3
1
Ix
+ =
( )






+ + = 2
2
2
D D - B
A
m
6
1
Iy
2
( )






+ + =
2
2
2
D D - B
A
m
6
1
Iz
2
ρ L R m
2
π =
( ) { }
θ θ
2 2 2 2
sin L cos 1 3R
m
12
1
I
+ + ×
=
θ
R
L
θ
R
ρ π
3
R
3
4
m =
2
R m
5
2
I
=