9
Subject to change without notice
Displayed wavelength L = 0.8div.,
set time coefficient Tc = 0.5µs/div.,
pressed X-MAG. (x10) button: Tc = 0.05µs/div.,
required rec. freq. F = 1:(0.8x0.05x10
-6
) = 25MHz,
required period T = 1:(25x10
6
) = 40ns.
If the time is relatively short as compared with the complete
signal period, an expanded time scale should always be
applied (X-MAG. (x10) active). In this case, the ascertained
time values have to be divided by 10. The time interval of
interest can be shifted to the screen center using the X-POS.
control.
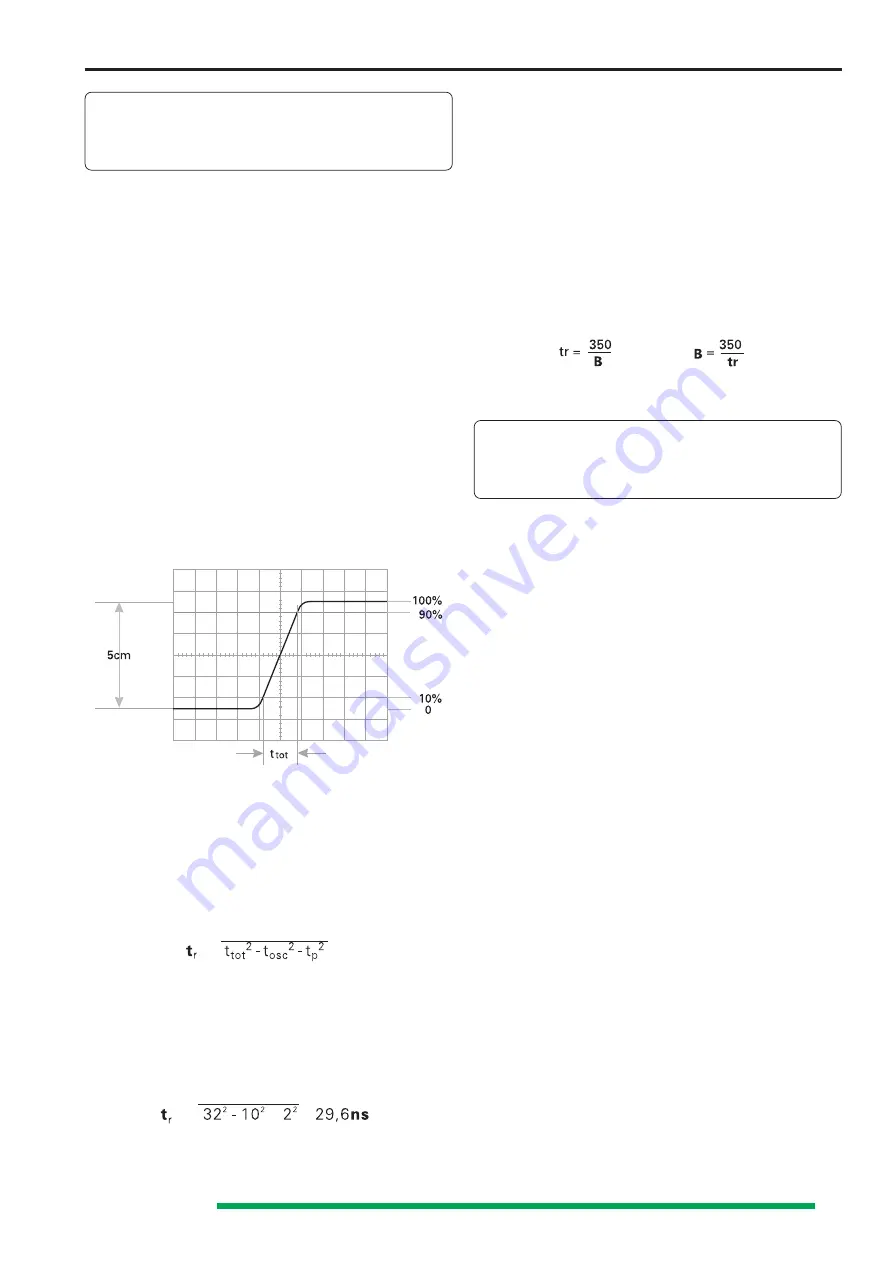
When investigating pulse or square waveforms, the critical
feature is the risetime of the voltage step. To ensure that
transients, ramp-offs, and bandwidth limits do not unduly
influence the measuring accuracy, the risetime is generally
measured between 10% and 90% of the vertical pulse height.
For measurement, adjust the Y deflection coefficient with
its variable control together with the Y-POS. control so that
the pulse height is precisely aligned with the 0% and 100%
lines of the internal graticule. The 10% and 90% points of
the signal will now coincide with the 10% and 90% graticule
lines. The risetime is given by the product of the horizontal
distance in div. between these two coincident points and the
time coefficient setting. If X x10 magnification is used, this
product must be divided by 10. The fall time of a pulse can
also be measured by using this method.
The following figure shows correct positioning of the
oscilloscope trace for accurate risetime measurement.
With a time coefficient of 0.2µs/div. and X x10 magnification,
the example shown in the above figure results in a total
measured risetime of
t
tot
= 1.6div x 0.2µs/div. : 10 =
32ns
When very fast risetimes are being measured, the risetimes
of the oscilloscope amplifier and of the attenuator probe has
to be deducted from the measured time value. The risetime
of the signal can be calculated using the following formula.
In this t
tot
is the total measured risetime, t
osc
is the risetime
of the oscilloscope amplifier (approx. 12ns), and t
p
the risetime
of the probe (e.g. = 2ns). If ttot is greater than 100ns, then
t
tot
can be taken as the risetime of the pulse, and calculation
is unnecessary.
Calculation of the example in the figure above results in a
signal risetime
The measurement of the rise or fall time is not limited to the
trace dimensions shown in the above diagram. It is only
particularly simple in this way. In principle it is possible to
measure in any display position and at any signal amplitude.
It is only important that the full height of the signal edge of
interest is visible in its full length at not too great steepness
and that the horizontal distance at 10% and 90% of the
amplitude is measured. If the edge shows rounding or
overshooting, the 100% should not be related to the peak
values but to the mean pulse heights. Breaks or peaks
(glitches) next to the edge are also not taken into account.
With very severe transient distortions, the rise and fall time
measurement has little meaning. For amplifiers with
approximately constant group delay (therefore good pulse
transmission performance) the following numerical
relationship between rise time
tr (in ns)
and bandwidth
B
(in MHz)
applies:
Connection of Test Signal
Caution! When connecting unknown signals to the
oscilloscope input, always use automatic triggering
and set the DC-AC input coupling switch to AC (DC
not lit). The attenuator should initially be set to 20V/
div.
Sometimes the trace will disappear after an input signal has
been applied. The attenuator must be switched to a higher
deflection coefficient by pressing the left (
<
) arrow pushbutton
in the VOLTS/DIV. section constantly or step by step, until
the vertical signal height is only 3-8div. With a signal amplitude
greater than 160Vpp, an attenuator probe must be inserted
before the vertical input. If, after applying the signal, the trace
is nearly blanked, the period of the signal is probably
substantially longer than the set value on the
TIME/DIV.
scale.
It should be switched to an adequately larger time coefficient
by pressing the left (
<
) arrow pushbutton in the
TIME/DIV
section by pressing it constantly or step by step. In most
cases the easiest way to adapt the instruments settings to
the input signal is to depress the
AUTO SET
pushbutton for
automatic instrument settings.
The signal to be displayed can be connected directly to the Y-
input of the oscilloscope with a shielded test cable such as
HZ32 or HZ34, or reduced through a x10 or x100 attenuator
probe. The use of test cables with high impedance circuits is
only recommended for relatively low frequencies (up to
approx. 50kHz). For higher frequencies, the signal source
must be of low impedance, i.e. matched to the characteristic
resistance of the cable (as a rule 50
Ω
). Especially when
transmitting square and pulse signals, a resistor equal to the
characteristic impedance of the cable must also be connected
across the cable directly at the Y-input of the oscilloscope.
When using a 50
Ω
cable such as the HZ34, a 50
Ω
through
termination type HZ22 is available from HAMEG. When
transmitting square signals with short rise times, transient
phenomena on the edges and top of the signal may become
visible if the correct termination is not used. A terminating
resistance is sometimes recommended with sine signals as
well. Certain amplifiers, generators or their attenuators
maintain the nominal output voltage independent of frequency
only if their connection cable is terminated with the prescribed
resistance. Here it must be noted that the terminating resistor
HZ22 will only dissipate a maximum of 2Watts. This power
is reached with 10Vrms or at 28.3Vpp with sine signal.
If a x10 or x100 attenuator probe is used, no termination is
necessary. In this case, the connecting cable is matched
directly to the high impedance input of the oscilloscope. When
using attenuators probes, even high internal impedance
= √
= √
−
=
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
























