MCS260B
CORNERSTONE 260B MONOCHROMATORS
70
18 APPENDIX IV: GRATING PHYSICS TUTORIAL
18.1 THE GRATING EQUATION
A typical diffraction grating consists of a substrate, usually of an “optical material”, with a large
number of parallel grooves ruled or replicated in its surface and overcoated with a reflecting
material such as aluminum. The quality and spacing of the grooves are crucial to the performance
of the grating, but the basic grating equation may be derived by supposing a section through the
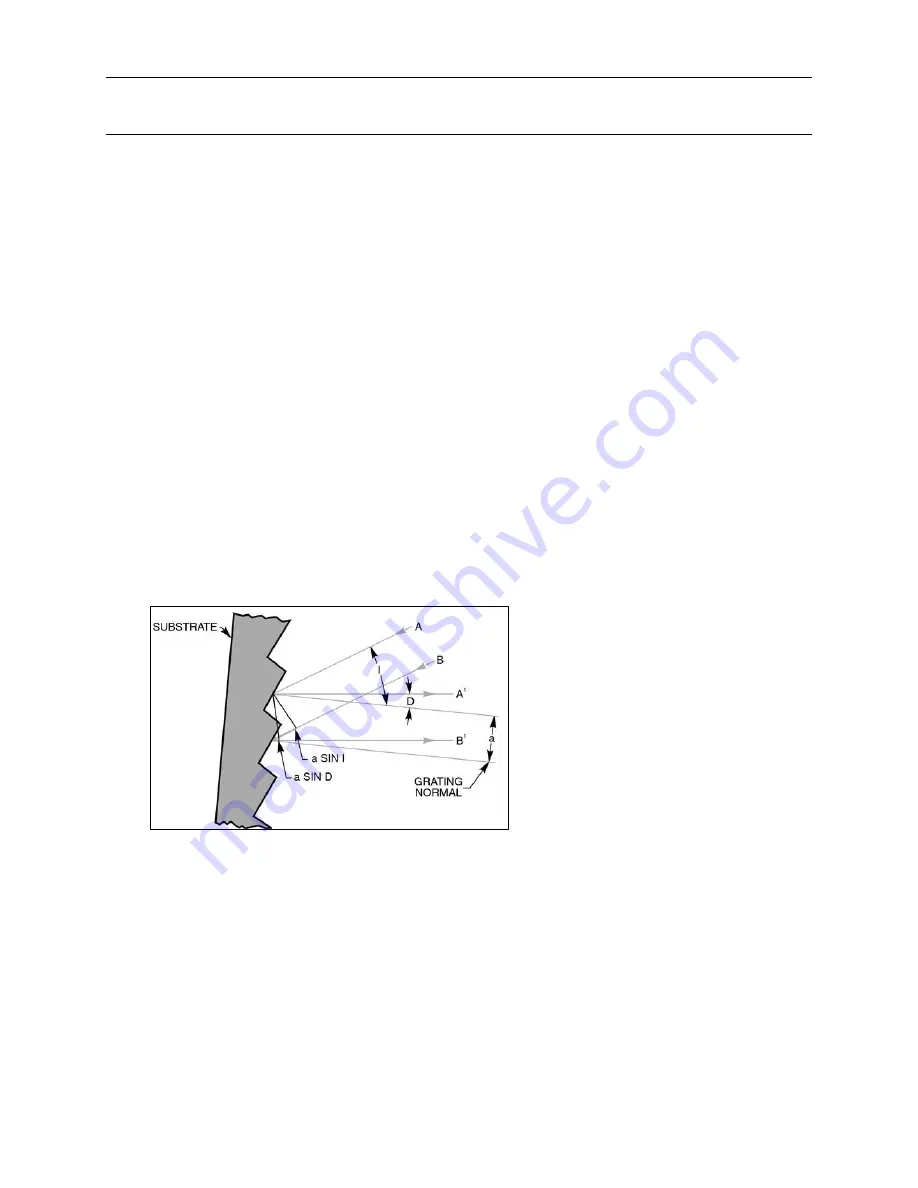
grating surface, normal to the ruling direction as a sawtooth pattern, shown below.
Light rays A and B, of wavelength λ, incident on adjacent grooves at angle I to the grating normal
are shown. Consider light at angle D to the grating normal; this light originates from the A and B
rays as they strike the grating. The path difference between the A1 and B1 rays can be seen to be:
a sin I + a sin D.
Summing of the rays A1 and B1 results in constructive interference if the path difference is equal to
any integer multiple of the wavelength λ:
a(
sin l+ sin D) = mλ
Where m is an integer, and is the order of diffraction
This is the basic grating equation. Note that if D is on the opposite side of the grating normal from I,
it is of the opposite sign.
We have considered only two grooves. Including all the other grooves does not change the basic
equation but sharpens the peak in the plot of diffracted intensity against angle D.
Figure 38: The Sawtooth Pattern of a Grating Section








































