9
Volume
A
B
Having shown that just three elements may define any sound, these elements now have to
be related to a Musical synthesizer. It is logical that a different section of the Synthesizer
‘synthesizes’ (or creates) these different elements.
One section of the synthesizer, the Oscillators, provide raw waveform signals which
define the pitch of the sound along with its raw harmonic content (tone). These signals
are then mixed together in a section called the Mixer, and the resulting mixture is then fed
into a section called the Filter. This makes further alterations to the tone of the sound, by
removing (filtering) or enhancing certain of the harmonics. Lastly, the filtered signal is fed
into the Amplifier, which determines the final volume of the sound.
Oscillators
Mixer
Filter
Amplifier
Additional synthesizer sections - LFOs and Envelopes - provide further ways of altering the
pitch, tone and volume of a sound by interacting with the Oscillators, Filter and
Amplifier, providing changes in the character of the sound which can evolve over time.
Because LFOs’ and Envelopes’ only purpose is to control (modulate) the other
synthesizer sections, they are commonly known as ‘modulators’.
These various synthesizer sections will now be covered in more detail.
The Oscillators And Mixer
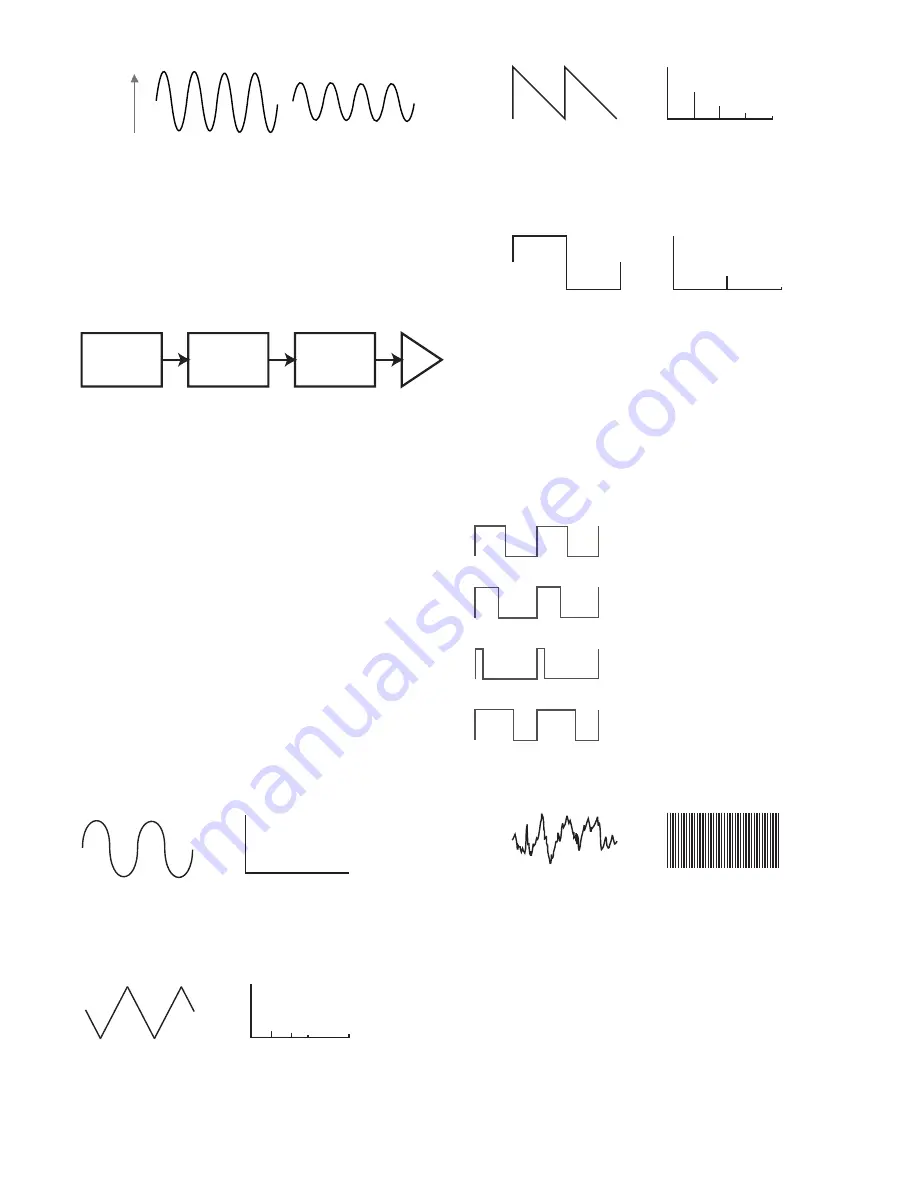
The Oscillator is really the heartbeat of the Synthesizer. It generates an electronic wave
(which creates the vibrations when eventually fed to a loudspeaker). This Waveform is
produced at a controllable musical pitch, initially determined by the note played on the
keyboard or contained in a received MIDI note message. The initial distinctive tone or
timbre of the waveform is actually determined by the waveform’s shape.
Many years ago, pioneers of musical synthesis discovered that just a few distinctive
waveforms contained many of the most useful harmonics for making musical sounds. The
names of these waves reflect their actual shape when viewed on an instrument called an
Oscilloscope, and these are: Sine waves, Square waves, Sawtooth waves, Triangle waves
and Noise.
Each waveform shape (except noise) has a specific set of musically-related harmonics
which can be manipulated by further sections of the synthesizer.
The diagrams below show how these waveforms look on an oscilloscope, and illustrate
the relative levels of their harmonics. Remember, it is the relative levels of the various
harmonics present in a waveform which determine the tone of the final sound.
Sine Waves
These possess just a single harmonic. A sine waveform produces the “purest” sound
because it only has its single pitch (frequency).
Triangle Waves
Volume
Harmonic
1
Sine Wave
Sawtooth Wave
Volume
Volume
Harmonic
Square Wave
Volume
Harmonic
1
2
3
4
5
Volume
Harmonic
1
3
5
7
Triangle Wave
1
2
3
4
5
Harmonic
1
2
3
4
5
Noise
These contain only odd harmonics. The volume of each decreases as the square of its
position in the harmonic series. For example, the 5th harmonic has a volume 1/25th of the
volume of the fundamental.
Sawtooth Waves
Volume
Harmonic
1
Sine Wave
Sawtooth Wave
Volume
Volume
Harmonic
Square Wave
Volume
Harmonic
1
2
3
4
5
Volume
Harmonic
1
3
5
7
Triangle Wave
1
2
3
4
5
Harmonic
1
2
3
4
5
Noise
These are rich in harmonics, and containing both even and odd harmonics of the
fundamental frequency. The volume of each is inversely proportional to its position in the
harmonic series.
Square / Pulse Waves
Volume
Harmonic
1
Sine Wave
Sawtooth Wave
Volume
Volume
Harmonic
Square Wave
Volume
Harmonic
1
2
3
4
5
Volume
Harmonic
1
3
5
7
Triangle Wave
1
2
3
4
5
Harmonic
1
2
3
4
5
Noise
These only have odd harmonics, which are at the same volume as the odd harmonics in a
sawtooth wave.
It will be noticed that the square waveform spends equal amounts of time in its ‘high’ state
and its ‘low’ state. This ratio is known as the ‘duty cycle’. A square wave always has a duty
cycle of 50% which means it is ‘high’ for half the cycle and ‘low’ for the other half.
In the MiniNova, it is possible to adjust the duty cycle of the basic square waveform to
produce a waveform which is more ‘rectangular’ in shape. These are often known as Pulse
waveforms. As the waveform becomes more and more rectangular, more even harmonics
are introduced and the waveform changes its character, becoming more ‘nasal’ sounding.
The width of the pulse waveform (the ‘Pulse Width’) can be altered dynamically by a
modulator, which results in the harmonic content of the waveform constantly changing. This
can give the waveform a very ‘fat’ quality when the pulse width is altered at a moderate rate.
50%
40%
10%
60%
It does not make any difference to how
a pulse waveform sounds whether the
duty cycle is 40% or 60%, since the
waveform is just “inverted” and the
harmonic content is exactly the same.
Noise Waves
Volume
Harmonic
1
Sine Wave
Sawtooth Wave
Volume
Volume
Harmonic
Square Wave
Volume
Harmonic
1
2
3
4
5
Volume
Harmonic
1
3
5
7
Triangle Wave
1
2
3
4
5
Harmonic
1
2
3
4
5
Noise
These are basically random signals, and have no one fundamental frequency (and therefore
no pitch property). All frequencies are at the same volume. Because they possess no pitch,
noise signals are often useful for creating sound effects and percussion type sounds.
Digital Waveforms
In addition to the traditional types of Oscillator waveforms detailed above, the MiniNova
also offers a set of carefully selected, digitally-generated waveforms containing useful
harmonic elements normally difficult to produce using traditional Oscillators.
Wavetables
A “wavetable” is essentially a group of digital waveforms. The MiniNova’s 36 wavetables
each contain 9 separate digital waveforms. The benefit of a wavetable is that consecutive
waveforms in the wavetable can be blended. Some of the MiniNova’s wavetables contain
waveforms with similar harmonic content, while others contain waveforms with greatly
differing harmonic content. Wavetables come alive when the ‘wavetable index’ – the
position within the wavetable - is modulated, resulting in a sound that continually changes
character, either smoothly or abruptly.
Volume
Harmonic
1
Sine Wave
Sawtooth Wave
Volume
Volume
Harmonic
Square Wave
Volume
Harmonic
1
2
3
4
5
Volume
Harmonic
1
3
5
7
Triangle Wave
1
2
3
4
5
Harmonic
1
2
3
4
5
Noise




































