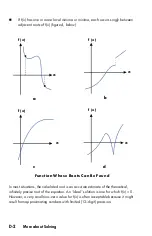
D-7
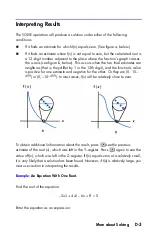
Now, solve to find the root:
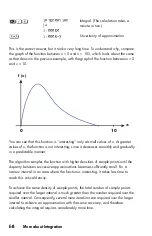
Note the difference between the last two estimates, as well as the relatively large
value for
f(x)
. The problem is that there is no value of
x
for which
f(x)
equals zero.
However, at
x
= 1.99999999999, there is a neighboring value of
x
that yields an
opposite sign for
f(x).
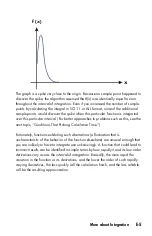
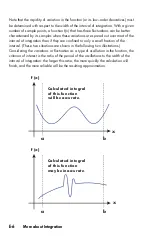
Example:
Find the root of the equation
As
x
approaches
,
f(x)
becomes a very large positive or negative number.
Enter the equation as an expression.
Keys:
Display:
Description:
X
_
Your initial guesses for the root.
Selects Equation mode; displays
the equation.
X
Finds a root with guesses 0 and 5.
Shows root, to 11 decimal places.
The previous estimate is slightly
bigger.
f(x)
is relatively large.
Keys:
Display:
Description:
Selects Equation mode.
X
4
X
Õ
Enters the equation.
0
1
6
2
=
−
−
x
x
6
Summary of Contents for 35s
Page 1: ...HP 35s scientific calculator user s guide H Edition 1 HP part number F2215AA 90001 ...
Page 14: ...12 Contents ...
Page 15: ...Part 1 Basic Operation ...
Page 16: ......
Page 46: ...1 30 Getting Started ...
Page 63: ...RPN The Automatic Memory Stack 2 17 A Solution ...
Page 64: ...2 18 RPN The Automatic Memory Stack ...
Page 74: ...3 10 Storing Data into Variables ...
Page 180: ...12 14 Statistical Operations ...
Page 181: ...Part 2 Programming ...
Page 182: ......
Page 246: ...15 12 Solving and Integrating Programs ...
Page 270: ...16 24 Statistics Programs ...
Page 284: ...17 14 Miscellaneous Programs and Equations ...
Page 285: ...Part 3 Appendixes and Reference ...
Page 286: ......
Page 308: ...B 8 User Memory and the Stack ...
Page 322: ...C 14 ALG Summary ...
Page 336: ...D 14 More about Solving ...
Page 346: ...E 10 More about Integration ...
Page 352: ...F 6 Messages ...
Page 370: ...G 18 Operation Index ...
Page 382: ...Index 12 ...