App-9
IM WT310E-01EN
Appendix
1
2
3
4
5
6
7
8
App
Index
AC Power
AC power cannot be determined as easily as DC power, because of the phase difference between the
voltage and current caused by load.
If the instantaneous voltage u = Umsinωt and the instantaneous current i = Imsin(ωt – Φ), the
instantaneous AC power p is as follows:
p = u×i = U
m
sin
ω
t×I
m
sin(
ωt – Φ) = UIcosΦ – UIcos(2ωt – Φ
)
U and I represent the rms voltage and rms current, respectively.
p is the sum of the time-independent term, UIcosΦ, and the AC component term of the voltage or
current at twice the frequency, –UIcos(2ωt – Φ).
AC power refers to the mean power over 1 period. When the mean over 1 period is taken, AC power P
is as follows:
P = UIcos
Φ [W]
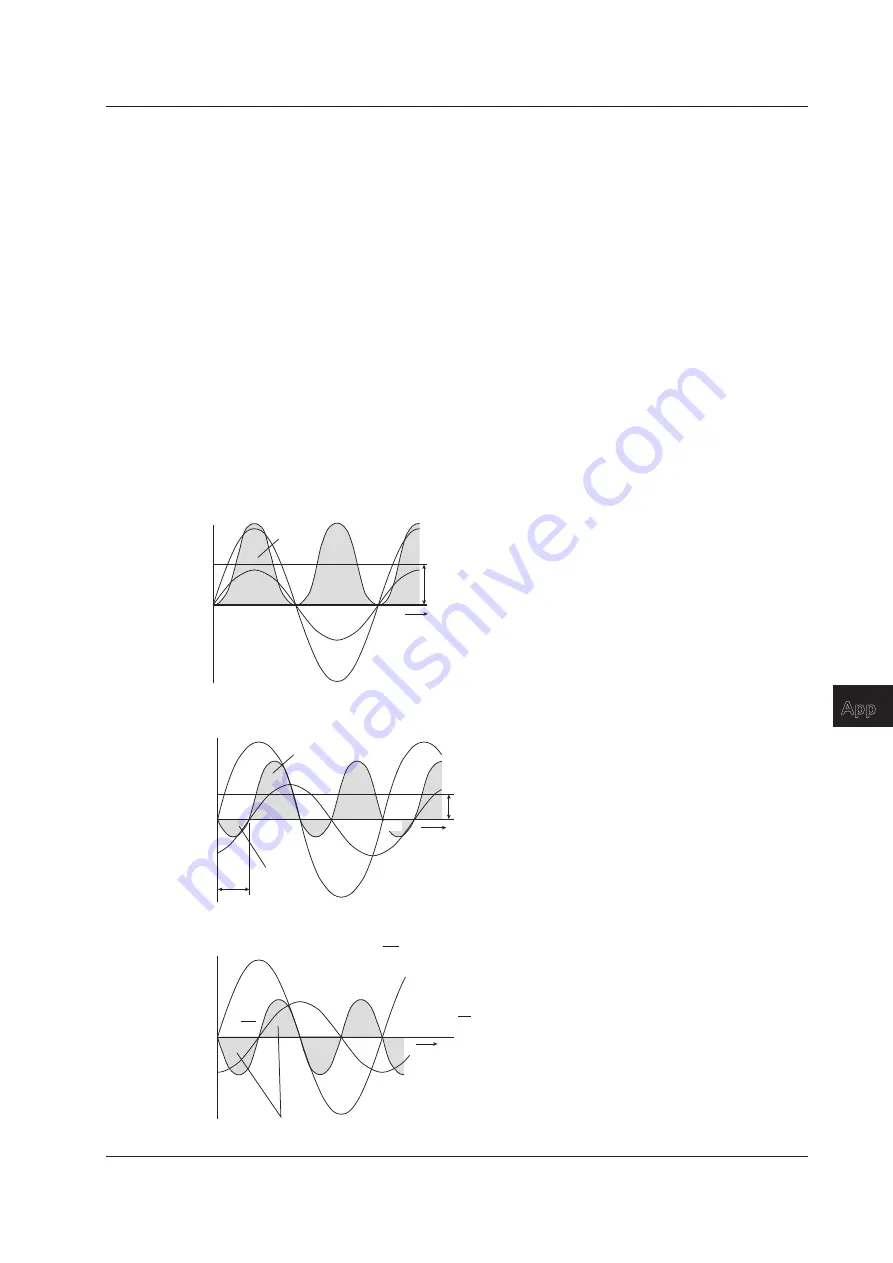
Even if the voltage and current are the same, the power varies depending on the phase difference Φ.
The section above the horizontal axis in the figure below represents positive power (power supplied
to the load), and the section below the horizontal axis represents negative power (power fed back
from the load). The difference between the positive and negative powers is the power consumed by
the load. As the phase difference between the voltage and current increases, the negative power
increases. At Φ = π/2, the positive and negative powers are equal, and the load consumes no power.
p
0
π
2
π
i
u
ω
t
Average power
P = UI
When the phase difference
between voltage and current is 0
Positive
power
p
0
π
i
u
ω
t
Average power
P = UIcosΦ
Negative
power
Φ
Positive power
When the phase difference
between voltage and current is Φ
2
π
p
0
2
π
i
u
ω
t
Average power
P = UIcos
The positive and negative powers are the same.
2
π
= 0
2
π
When phase difference
between voltage and current is 2
π
π
Appendix 2 Power Basics (Power, harmonics, and AC RLC circuits)
















































