App-6
IM WT310E-01EN
Appendix 2 Power Basics (Power, harmonics, and
AC RLC circuits)
This section explains the basics of power, harmonics, and AC RLC circuits.
Power
Electrical energy can be converted into other forms of energy and used. For example, it can be
converted into the heat in an electric heater, the torque in a motor, or the light in a fluorescent or
mercury lamp. In these kinds of examples, the work that electricity performs in a given period of time (or
the electrical energy expended) is referred to as electric power. The unit of electric power is watts (W).
1 watt is equivalent to 1 joule of work performed in 1 second.
DC Power
The DC power P (in watts) is determined by multiplying the applied voltage U (in volts) by the current I (in
amps).
P = UI [W]
In the example below, the amount of electrical energy determined by the equation above is retrieved
from the power supply and consumed by resistance R (in ohms) every second.
R
I
U
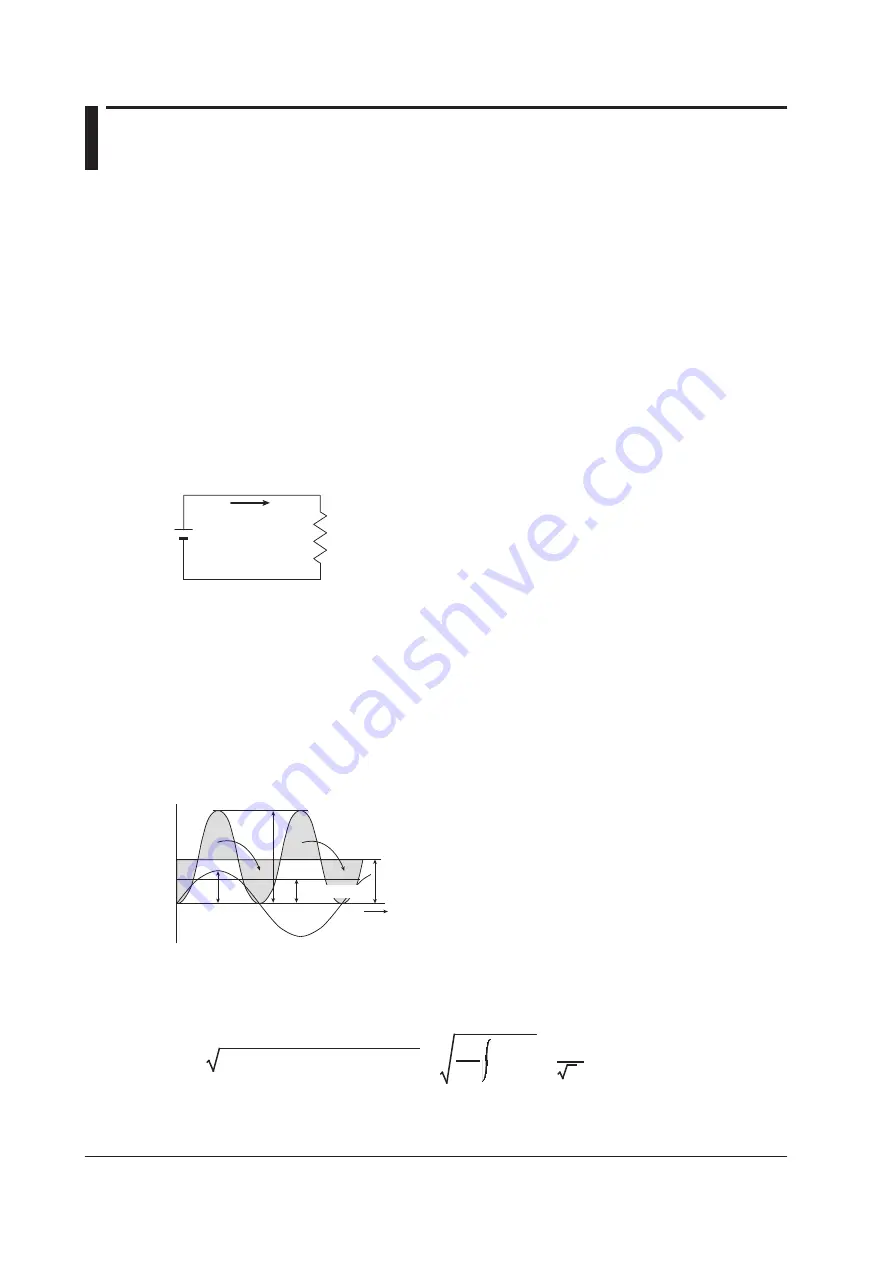
Alternating Current
Normally, the power supplied by power companies is alternating current with sinusoidal waveforms.
The magnitude of alternating current can be expressed using values such as instantaneous, maximum,
rms, and mean values. Normally, it is expressed using rms values.
The instantaneous value i of a sinusoidal alternating current is expressed by Imsinωt (where Am is the
maximum value of the current, ω is the angular velocity defined as ω = 2πf, and f is the frequency of
the sinusoidal alternating current). The thermal action of this alternating current is proportional to i
2
,
and varies as shown in the figure below.*
* Thermal action is the phenomenon in which watt hour is converted to heat energy when a current
flows through a resistance.
π
2
π
ω
t
i = Imsinωt
i
2
I
m
I
m
2
Rms value I
Average of i
2
The areas are the same.
The rms value (effective value) is the DC value that generates the same thermal action as the
alternating current. With I as the DC value that produces the same thermal action as the alternating
current:
I=
The mean of i
2
over one period =
=
1
2
π
0
2
π
i
2
d
ω
t
I
m
2
Because this value corresponds to the root mean square of the instantaneous values over 1 period,
the effective value is normally denoted using the abbreviation “rms.”






























