Approach
The example shows the calculation of the minimum distance in accordance with ISO
13855 for an orthogonal (right-angled) approach to the protective field. A different cal‐
culation may be required depending on the application and the ambient conditions
(e.g., for a protective field parallel to or at any angle to the direction of approach or an
indirect approach).
1.
First calculate S with the following formula:
S = 2,000 mm/s × T + 8 ×(d – 14 mm)
where:
°
S = minimum distance in millimeters (mm)
°
T = machine stopping time + response time of the protective device after
interruption in the light path in seconds (s)
°
d = resolution of the safety light curtain in millimeters (mm)
The reach or approach speed is already included in the formula.
2.
If the result S is ≤ 500 mm, then use the determined value as the minimum dis‐
tance.
3.
If the result S is > 500 mm, then recalculate S as follows:
S = 1,600 mm/s × T + 8 ×(d – 14 mm)
4.
If the new value S is > 500 mm, then use the newly determined value as the mini‐
mum distance.
5.
If the new value S is ≤ 500 mm, then use 500 mm.
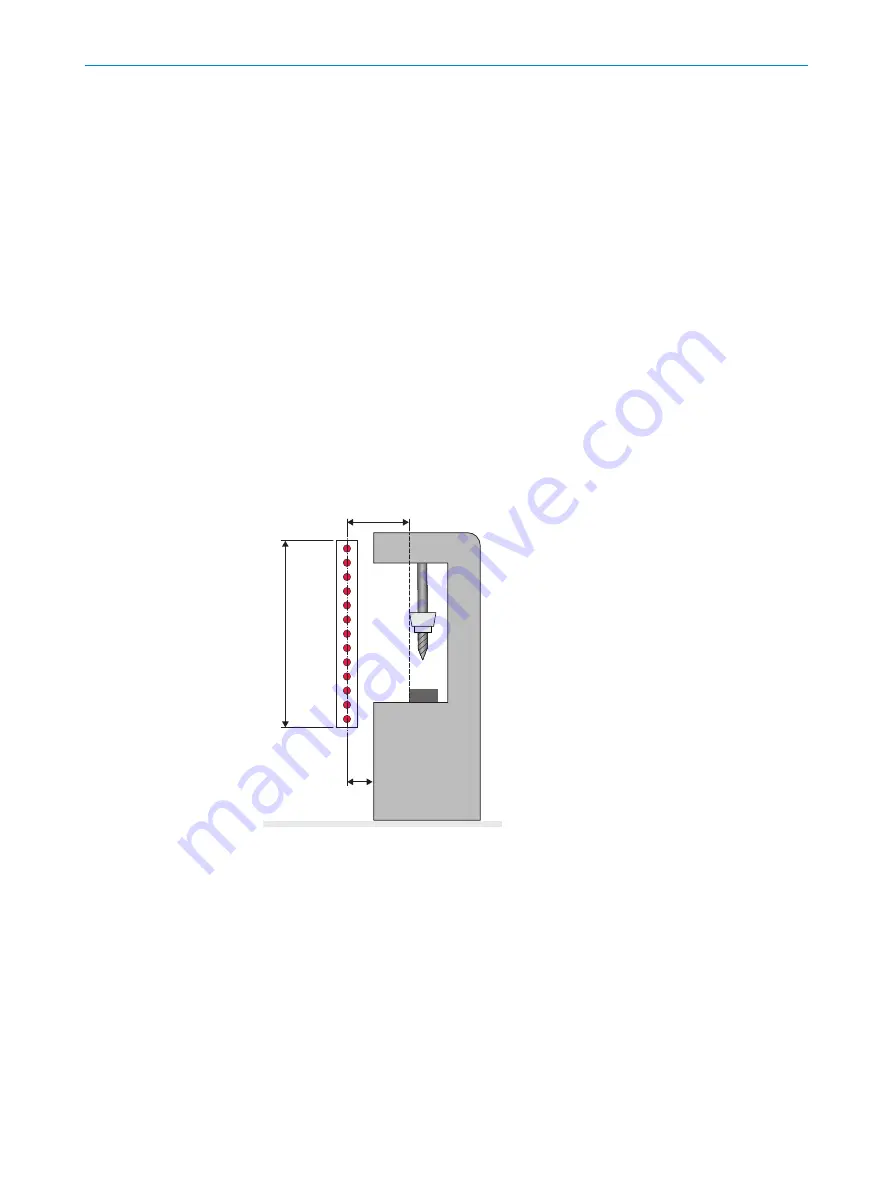
!
"
§
S
Figure 12: Minimum distance to hazardous point for orthogonal (right-angled) approach to pro‐
tective field
!
Protective field height
"
Hazardous point
§
Depending on the application and distance, persons must be prevented from standing
behind the protective device.
Example calculation
Machine stopping time = 290 ms
Response time after interruption of the light path = 30 ms
Resolution of the safety light curtain = 14 mm
T = 290 ms + 30 ms = 320 ms = 0.32 s
S = 2,000
mm/s × 0.32
s + 8 × (14
mm – 14
mm) = 640 mm
4
PROJECT PLANNING
24
O P E R A T I N G I N S T R U C T I O N S | miniTwin4
8012624/10OM/2018-08-09 | SICK
Subject to change without notice
















































