HP 50G, Руководство пользователя

Страница: 493 / 887

Page 16-16
You can prove that L{H(t)} = 1/s,
from which it follows that L{U
o
⋅
H(t)} = U
o
/s,
where U
o
is a constant. Also, L
-1
{1/s}=H(t),
and L
-1
{ U
o
/s}= U
o
⋅
H(t).
Also, using the shift theorem for a shift to the right, L{f(t-a)}=e
–as
⋅
L{f(t)} =
e
–as
⋅
F(s), we can write L{H(t-k)}=e
–ks
⋅
L{H(t)} = e
–ks
⋅
(1/s) = (1/s)
⋅
e
–ks
.
Another important result, known as the second shift theorem for a shift to the
right, is that L
-1
{e
–as
⋅
F(s)}=f(t-a)
⋅
H(t-a), with F(s) = L{f(t)}.
In the calculator the Heaviside step function H(t) is simply referred to as ‘1’. To
check the transform in the calculator use:
1 `
LAP. The result is ‘1/X’, i.e.,
L{1} = 1/s. Similarly, ‘U0’
`
LAP , produces the result ‘U0/X’, i.e., L{U
0
}
= U
0
/s.
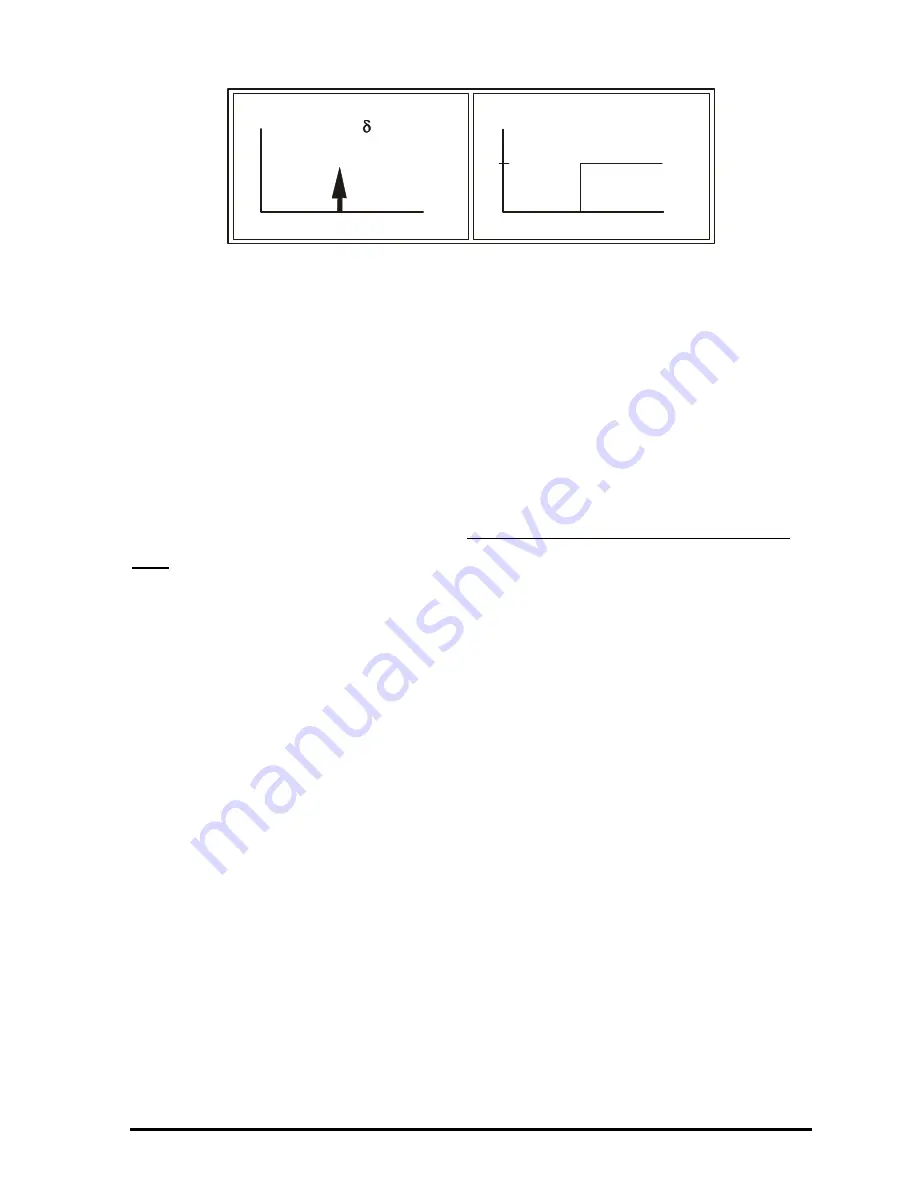
You can obtain Dirac’s delta function in the calculator by using:
1`
ILAP
The result is
‘
Delta(X)
’
.
This result is simply symbolic, i.e., you cannot find a numerical value for, say
‘
Delta(5)
’.
This result can be defined the Laplace transform for Dirac’s delta function,
because from L
-1
{1.0}=
δ
(t), it follows that L{
δ
(t)} = 1.0
Also, using the shift theorem for a shift to the right, L{f(t-a)}=e
–as
⋅
L{f(t)} =
e
–as
⋅
F(s), we can write L{
δ
(t-k)}=e
–ks
⋅
L{
δ
(t)} = e
–ks
⋅
1.0 = e
–ks
.
y
x
x
0
(x_x )
0
H(x_x )
0
x
0
y
x
1